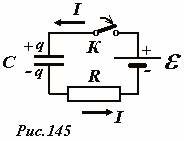
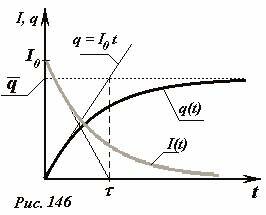
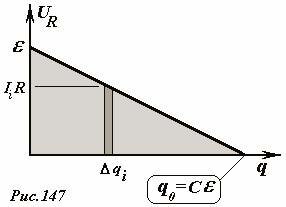
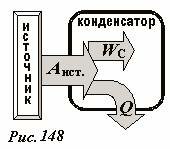
Энергия заряженного конденсатора — когда потенциал обкладки конденсатора, на которой находится заряд Или можно преобразовать В формуле мы использовали : xn--b1agsdjmeuf9e.xn--p1ai Содержание книги Предыдующая страница Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее. Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ε (Рис. 145). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим R. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе \(~U_C = \frac{q}{C}\) и резисторе \(U_R = IR\) равна ЭДС источника \(\varepsilon = U_C + U_R\), что приводит к уравнению В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи \(~I = \frac{\Delta q}{\Delta t}\), что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t и (t + Δt), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Δε = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Δ , поэтому полученное уравнение приобретает вид Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда) Математическая смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I0 = I(0). С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко. В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна \(~I_0 = \Delta \left (\frac{\Delta q}{\Delta t} \right )_0 = \frac{\varepsilon}{R}\). Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения \(~\overline{q} = C\varepsilon\) и ток в цепи прекратится. Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату. Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда. Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса. Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора. Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника. На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q, то сторонние силы совершили при этом работу A0 = qε , при этом энергия конденсатора стала равной \(~W = \frac{q^2}{2C} = \frac{q \varepsilon}{2}\) , что в два раза меньше работы совершенной источником. Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Δti (i = 1,2,3...). Перепишем уравнение (1) в виде и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Δti, Δqi = IiΔti . В результате получим Здесь обозначено qi - заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл: \[~\varepsilon \Delta q_i = \delta A\] - работа сторонних сил по перемещению порции заряда Δqi; \[~\frac{q_i}{C} \Delta q_i = \Delta W_C\] - увеличение энергии конденсатора при увеличении его заряда на Δqi; \[~I_i R \Delta q_i = I^2_i R \Delta t_i = \delta Q\] - количество теплоты, выделившееся на резисторе, при протекании порции заряда Δqi. Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки. Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим: \[~\sum_i \varepsilon \Delta q_i = \varepsilon \overline{q} = A\] - полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора; \[~\sum_i \frac{q_i}{C} \Delta q_i = \frac{\overline{q^2}}{2C} = \frac{\varepsilon \overline{q}}{2} = \frac{C \varepsilon^2}{2}\] - энергия заряженного конденсатора; Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе \(U_R = IR\) от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии. За малый промежуток времени через резистор протечет малый заряд Δqi, при этом выделится количество теплоты \(~\delta Q_i = I_i R \Delta q_i\), которое численно равно площади узкой полоски, выделенной на рисунке. Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости UR(q), то есть Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энергии конденсатора и количества выделившейся теплоты \(A = W_C + Q\). Схематически преобразование энергии в этом процессе показано на рис. 148. Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энергии конденсатора. То есть, половина энергии источника переходит в энергию электрического поля, а вторая в тепловую энергию, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора[1]. Следующая страница www.physbook.ru Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах. Но прежде введём понятие электрической ёмкости. Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым. Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать Величина Например, потенциал уединённого шара в вакууме равен: где Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз: Соответственно, ёмкость шара в раз увеличивается: Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов. Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит. В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В. Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным Как видите, Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2): Следовательно, диэлектрическая постоянная может измеряться в Ф/м: Ф. Так легче запомнить, не правда ли? Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл. Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников. Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров. Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух Пусть заряды обкладок равны и Пусть Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости: Здесь На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора. Рис. 1. Электрическое поле плоского конденсатора Согласно принципу суперпозиции, для результирующего поля имеем: Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга): Внутри конденсатора поле удваивается: или Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак: Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами. Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок. Пусть расстояние между обкладками конденсатора равно Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками: Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора: Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора? Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем: Соответственно, напряжение на конденсаторе: Отсюда ёмкость плоского конденсатора с диэлектриком: Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор. Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость. Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу. Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора. Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора Возьмём на второй обкладке настолько маленькую площадку, что заряд где Следовательно, Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам). Результирующая сила Предположим теперь, что расстояние между обкладками изменилось от начальной величины Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть. С учётом формул (11) и (7) имеем: где Это можно переписать следующим образом: где Работа потенциальной силы Используя соотношение Особенно полезными являются формулы (12) и (14). Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим: При вычислении работы силы Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком. Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим. Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии: Но Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля. Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами. Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим: (16) В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости. Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь: (18) Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени. Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве) Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним. ege-study.ruВсе формулы. Заряд конденсатора формула
Энергия заряженного конденсатора | Все формулы
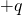 , равен
, равен  а потенциал обкладки, на которой находится заряд
а потенциал обкладки, на которой находится заряд  , равен
, равен  . Формула выглядит так:
. Формула выглядит так:![Rendered by QuickLaTeX.com \large W_p=\frac{1}{2}\left[(+q)\varphi _1 +(-q)\varphi _2 \right]= \frac{1}{2}q(\varphi _1-\varphi _2)=\frac{1}{2}qU](/800/600/http/XN--B1AGSDJMEUF9E.XN--P1AI/wp-content/uploads/2016/03/quicklatex.com-e4244fdea1f6352f73db80c2305a64f2_l3.png)


 — Энергия заряженного конденсатора
— Энергия заряженного конденсатора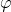 — Потенциал проводника
— Потенциал проводника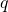 — Точечный заряд
— Точечный заряд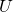 — Напряжение
— НапряжениеСлободянюк А.И. Физика 10/16.4 — PhysBook
§16. Превращение энергии в электрических и магнитных явлениях
16.4 Зарядка конденсатора от источника постоянной ЭДС.
Примечания
Конденсатор. Энергия электрического поля - материалы для подготовки к ЕГЭ по Физике
Ёмкость уединённого проводника
, так что
называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:
(1)
— заряд шара,
— его радиус. Отсюда ёмкость шара:
(2)
(3)
В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.
км.
мкФ.
Ф — это очень большая ёмкость.
Ёмкость плоского конденсатора
. Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина
— заряд положительной обкладки — называется зарядом конденсатора.
— площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
— напряжённость поля положительной обкладки,
— напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

(4)
. Поскольку поле внутри конденсатора является однородным, разность потенциалов
между обкладками равна произведению
на
(вспомните связь напряжения и напряжённости в однородном поле!):
(5)
(6)
В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
(7)
(8)
(9)
(10)
Энергия заряженного конденсатора
, площадь обкладок
.
этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
— напряжённость поля первой обкладки:
притяжения второй обкладки к первой складывается из всех этих сил
, с которыми притягиваются к первой обкладке всевозможные маленькие заряды
второй обкладки. При этом суммировании постоянный множитель
вынесется за скобку, а в скобке просуммируются все
и дадут
. В результате получим:
(11)
до конечной величины
. Сила притяжения пластин совершает при этом работу:
(12)
притяжения обкладок оказалась равна изменению со знаком минус величины
. Это как раз и означает, что
— потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
, из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
, как нетрудно видеть, величина войдёт в ёмкость
, и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Энергия электрического поля
— объём конденсатора. Получаем:
(15)
, сосредоточенного в некотором объёме
.
(17)
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''











Поделиться с друзьями: