Устная формулировка закона Ома такова: сила тока в проводнике прямо пропорциональна электродвижущей силе, приложенной к его концам, и обратно пропорциональна величине его электрического сопротивления. Общеупотребительные формулы, выражающие закон Ома и получаемые одна из другой путем соответствующих перестановок входящих в них величин, выглядят так: Эти формулы справедливы лишь в том случае, если сила тока I выражена в амперах, электродвижущая сила Е — в вольтах и сопротивление R— в омах. Разумеется, по формуле можно произвести правильный подсчет сопротивления и в том случае, если Е выразить в миливольтах, аI—в миллиамперах, но на первой ступени овладения электротехническими знаниями, во избежание грубых ошибок, лучше все расчеты, связанные с применением закона Ома, производить, пользуясь только лишь основными единицами измерения входящих в формулы величин. Для измерения больших сопротивлений пользуются производными единицами — килоомами (1 ком= 103 ом) и мегомами (1 мгом—106 ом). Малые сопротивления измеряются только в омах и долях ом. За рубежом омы, килоомы и мегомы обозначают соответственно Ω, KΩ и MΩ. С законом Ома в повседневных электротехнических расчетах приходится сталкиваться наиболее часто. Решим типичную задачу на применение закона Ома. .Определим, какое напряжение требуется для того, чтобы через сопротивление в 2 ком проходил ток 5 мка. Воспользуемся для этого формулой Е = IR, в которую подставим R =2000 ом и I = 5 мка = 5·10-6 а Другой пример. Какой ток пройдет через проводник с сопротивлением 25 ом под влиянием приложенного к его концам напряжения 100 в? Здесь все единицы основные, поэтому прямо подставляем наши данные в формулу и получаем результат Сопротивление проводников можно рассчитывать и по их геометрическим размерам, если известен материал, из которого они сделаны. Расчет ведется по формуле В этой формуле R будет получено в омах, если длина проводника l выражена в метрах, а площадь его поперечного сечения S—в квадратных миллиметрах. Коэффициент р называется удельным сопротивлением. Он имеет для разных металлов и сплавов значения, помещенные в табл. 2, численно равные выраженному в омах сопротивлению отрезка провода из данных материалов длиною в 1 м при площади поперечного сечения в 1 мм2. Значения ρ даны в таблице для температуры 20°. С изменением температуры тел меняются и их физические свойства (например, размеры, плотность и т. д.), вследствие чего изменяется также и их сопротивление. При повышении температуры медного провода, например, на 1000 его сопротивление увеличивается на 40%. В табл. 2 правая крайняя колонка содерαжит значения так называемого „температурного коэффициента сопротивления" различных материалов а, позволяющего учитывать изменения сопротивления проводников в зависимости от отклонений их температуры от условного начального уровня, равного 20°. Число α показывает, на какую долю первоначальной величины изменится сопротивление проводника при изменении его температуры на 1°. Таблица 2 Для вычисления сопротивления проводника Rt, соответствующего температуре t°, пользуются формулой Как правило, сплавов значительно меньше, чем для чистых металлов, а α угля, электролитов и полупроводников имеет даже отрицательное значение. Пользуясь приведенными выше формулами и табл. 2, нетрудно рассчитать точную величину сопротивления любого проводника по его размерам, если материал проводника и рабочая температура заданы заранее. Пример. Рассчитать величину сопротивления железной проволоки длиною 1 км диаметром 1 мм при температуре 0°. Помня, что площадь круга подставляем условия задачи сначала в формулу выражая длину l в метрах: Затем учитываем влияние температуры Закономерность, связывающая изменения сопротивления с изменениями температуры, позволяет решать и обратную задачу, т. е. определять температуру по данным сопротивления. Приборы, предназначенные для этого, называются термометрами сопротивления. 1 Проводник из ртути получают, наполняя стеклянную трубку соответствующих размеров. aerologiya.ru Зако́н О́ма — эмпирический физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника, установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома. В своей оригинальной форме он был записан его автором в виде : Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает Закон Ома для полной цепи: где: Из закона Ома для полной цепи вытекают следствия: Часто[2] выражение где Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется: То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС. К другой записи формулы (3), а именно: применима другая формулировка: Выражение (5) можно переписать в виде: где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому. В соответствии с этой диаграммой формально может быть записано выражение: которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно. В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника: где: Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока В таком случае потери мощности будут определяться выражением: Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт. Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. Сопротивление Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: где: Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред. Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига. Если ток является синусоидальным с циклической частотой где: При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций. В классическом приближении закон Ома можно вывести при помощи теории Друде: Здесь: Проводники и элементы, для которых соблюдается закон Ома, называются омическими. Закон Ома может не соблюдаться: wp.wiki-wiki.ru Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома. В своей оригинальной форме он был записан его автором в виде : , Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1]. В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает Закон Ома для полной цепи: , (2) где: Из закона Ома для полной цепи вытекают следствия: Часто[2] выражение: (3) (где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома». Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется: (4) То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС. К другой записи формулы (3), а именно: (5) Применима другая формулировка: Выражение (5) можно переписать в виде: (6) где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S). В соответствии с этой диаграммой формально может быть записано выражение: (7) Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно. В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника: (8) где: Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач). В таком случае потери мощности будут определяться выражением: = (9) Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт. Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: где: Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1). Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред. Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига. Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: где: При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда. Закон Ома можно просто объяснить при помощи теории Друде: Здесь: biograf.academic.ru Диаграмма – Закон Ома. На рис. показана схема знакомой вам простейшей электронной цепи. Эта замкнутая цепь состоит из 3-х частей: источника напряжения – батареи GB, потребителя тока – нагрузки R, которой может быть, к примеру, нить накала электронной лампы либо резистор, и проводников, соединяющих источник напряжения с нагрузкой. Меж иным, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря.Меж иным, если эту цепь дополнить выключателем, то получится полная схема карманного электронного фонаря. Нагрузка R, владеющая определенным сопротивлением, является участком цепи. Значение тока на этом участке цепи находится в зависимости от действующего на нем напряжения и его сопротивления: чем больше напряжение и меньше сопротивление, тем огромным ток будет идти по участку цепи. Эта зависимость тока от напряжения и сопротивления выражается последующей формулой: I = U/R,где I – ток, выраженный в амперах, А; U – напряжение в вольтах, В; R – сопротивление в омах, Ом. Читается это математическое выражение так: ток на участке цепи прямо пропорционален напряжению на нем и назад пропорционален его сопротивлению. Это основной закон электротехники, называемый законом Ома (по фамилии Г. Ома), для участка электронной цепи. Используя закон Ома, можно по двум известным электронным величинам выяснить неведомую третью. Вот несколько примеров практического внедрения закона Ома. 1-ый пример: На участке цепи, владеющем сопротивлением 5 Ом, действует напряжение 25 В. Нужно выяснить значение тока на этом участке цепи.Решение: I = U/R = 25 / 5 = 5 А.2-ой пример: На участке цепи действует напряжение 12 В, создавая в нем ток, равный 20 мА. Каково сопротивление этого участка цепи? Сначала ток 20 мА необходимо выразить в амперах. Это будет 0,02 А. Тогда R = 12 / 0,02 = 600 Ом. 3-ий пример: Через участок цепи сопротивлением 10 кОм течет ток 20 мА. Каково напряжение, действующее на этом участке цепи? Тут, как и в прошлом примере, ток должен быть выражен в амперах (20 мА = 0,02 А), сопротивление в омах (10кОм = 10000Ом). Как следует, U = IR = 0,02 х 10000 = 200 В. На цоколе лампы накаливания плоского карманного фонаря выштамповано: 0,28 А и 3,5 В. О чем молвят эти сведения? О том, что лампочка будет нормально сиять при токе 0,28 А, который обусловливается напряжением 3,5 В, Пользуясь законом Ома, несложно подсчитать, что накаленная нить лампочки имеет сопротивление R = 3,5 / 0,28 = 12,5 Ом. Это, подчеркиваю, сопротивление накаленной нити лампочки. А сопротивление остывшей нити существенно меньше. Закон Ома справедлив не только лишь для участка, да и для всей электронной цепи. В данном случае в значение R подставляется суммарное сопротивление всех частей цепи, в том числе и внутреннее сопротивление источника тока. Но при простых расчетах цепей обычно третируют сопротивлением соединительных проводников и внутренним сопротивлением источника тока. В связи с этим приведу очередной пример: Напряжение электроосветительной сети 220 В. Какой ток потечет в цепи, если сопротивление нагрузки равно 1000Ом? Решение: I = U/R = 220 / 1000 = 0,22 А. Приблизительно таковой ток потребляет электронный паяльничек. Всеми этими формулами, вытекающими из закона Ома, можно воспользоваться и для расчета цепей переменного тока, но при условии, если в цепях нет катушек индуктивности и конденсаторов. Закон Ома и производные от него расчетные формулы, довольно просто уяснить, если воспользоваться вот этой графической схемой, т. н. треугольник закона Ома: Воспользоваться этим треугольником просто, довольно верно уяснить, что горизонтальная линия в треугольнике значит символ деления (по аналогии дробной черты), а вертикальная линия в треугольнике значит символ умножения. Сейчас разглядим таковой вопрос: как оказывает влияние на ток резистор, включаемый в цепь поочередно с нагрузкой либо параллельно ей? Разберем таковой пример. У нас имеется лампочка от круглого электронного, фонаря, рассчитанная на напряжение 2,5 В и ток 0,075 А. Можно ли питать эту лампочку от батареи 3336Л, изначальное напряжение которой 4,5 В? Несложно подсчитать, что накаленная нить этой лампочки имеет сопротивление немногим больше 30 Ом. Если же питать ее от свежайшей батареи 3336Л, то через нить накала лампочки, по закону Ома, пойдет ток, практически в два раза превосходящий тот ток, на который она рассчитана. Таковой перегрузки нить не выдержит, она перекалится и разрушится. Но эту лампочку все таки можно питать от батареи 336Л, если поочередно в цепь включить дополнительный резистор сопротивлением 25 Ом, как это показано на рис.. В данном случае общее сопротивление наружной цепи будет равно приблизительно 55 Ом, т.е. 30 Ом – сопротивление нити лампочки Н плюс 25 Ом – сопротивление дополнительного резистора R. В цепи, как следует, потечет ток, равный приблизительно 0,08 А, т.е. практически таковой же, на который рассчитана нить накала лампочки. Эту лампочку можно питать от батареи и с более высочайшим напряжением и даже от электроосветительной сети, если подобрать резистор соответственного сопротивления. В этом примере дополнительный резистор ограничивает ток в цепи до подходящего нам значения. Чем больше будет его сопротивление, тем меньше будет и ток в цепи. В этом случае в цепь было включено поочередно два сопротивления: сопротивление нити лампочки и сопротивление резистора. А при поочередном соединении сопротивлений ток схож во всех точках цепи. Можно включать амперметр в всякую точку цепи, и везде он будет демонстрировать одно значение. Это явление можно сопоставить с потоком воды в реке. Русло реки на разных участках может быть широким либо узеньким, глубочайшим либо маленьким. Но за определенный просвет времени через поперечное сечение хоть какого участка русла реки всегда проходит однообразное количество воды. Дополнительный резистор, включаемый в цепь поочередно с нагрузкой (как, к примеру, на рис. выше), можно рассматривать как резистор, «гасящий» часть напряжения, действующего в цепи. Напряжение, которое гасится дополнительным резистором либо, как молвят, падает на нем, будет тем огромным, чем больше сопротивление этого резистора. Зная ток и сопротивление дополнительного резистора, падение напряжения на нем просто подсчитать все по той же знакомой вам формуле U = IR, Тут U – падение напряжения, В; I – ток в цепи, A; R – сопротивление дополнительного резистора, Ом. Применительно к нашему примеру резистор R ( на рис.) погасил излишек напряжения: U = IR = 0,08 х 25 = 2 В. Остальное напряжение батареи, равное примерно 2,5 В, свалилось на нити лампочки. Нужное сопротивление резистора можно отыскать по другой знакомой вам формуле R = U/I, где R – разыскиваемое сопротивление дополнительного резистора, Ом; U-напряжение, которое нужно погасить, В; I – ток в цепи, А. Для нашего примера сопротивление дополнительного резистора равно: R = U/I = 2/0,075, 27 Ом. Изменяя сопротивление, можно уменьшать либо наращивать напряжение, которое падает на дополнительном резисторе, и таким макаром регулировать ток в цепи. Но дополнительный резистор R в таковой цепи может быть переменным, т.е. резистором, сопротивление которого можно изменять (см. рис. ниже). В данном случае при помощи движка резистора можно плавненько изменять напряжение, подводимое к нагрузке Н, а означает, плавненько регулировать ток, протекающий через эту нагрузку. Включенный таким макаром переменный резистор именуют реостатом, При помощи реостатов регулируют токи в цепях приемников, телевизоров и усилителей. В почти всех кинозалах реостаты использовали для плавного гашения света в зрительном зале. Есть, но, и другой метод подключения нагрузки к источнику тока с лишним напряжением – тоже при помощи переменного резистора, но включенного потенциометром, т.е. делителем напряжения, как показано на рис.. Тут R1 – резистор, включенный потенциометром, a R2 – нагрузка, которой может быть та же лампочка накаливания либо какой – то другой прибор. На резисторе R1 происходит падение напряжения источника тока, которое отчасти либо стопроцентно может быть подано к нагрузке R2. Когда движок резистора находится в последнем нижнем положении, к нагрузке напряжение вообщем не подается (если это лампочка, она пылать не будет). По мере перемещения движка резистора ввысь мы будем подавать все большее напряжение к нагрузке R2 (если это лампочка, ее нить будет накаливаться). Когда же движок резистора R1 окажется в последнем верхнем положении, к нагрузке R2 будет подано все напряжение источника тока (если R2 – лампочка карманного фонаря, а напряжение источника тока огромное, нить лампочки перегорит). Можно опытным методом отыскать такое положение движка переменного резистора, при котором к нагрузке будет подано нужное ей напряжение. Переменные резисторы, включаемые потенциометрами, обширно употребляют для регулирования громкости в приемниках и усилителях. Резистор может быть конкретно подключен параллельно нагрузке. В таком случае ток на этом участке цепи разветвляется и идет 2-мя параллельными способами: через дополнительный резистор и основную нагрузку. Больший ток будет в ветки с минимальным сопротивлением. Сумма же токов обеих веток будет равна току, используемому на питание наружной цепи. К параллельному соединению прибегают в тех cлучаях, когда нужно ограничить ток не во всей цепи, как при поочередном включении дополнительного резистора, а лишь на каком – то участке. Дополнительные резисторы подключают, к примеру, параллельно миллиамперметрам, чтоб ими можно было определять огромные токи. Такие резисторы называют шунтирующими или шунтами. Слово шунт означает ответвление. elektrica.info Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома. В своей оригинальной форме он был записан его автором в виде : , Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1]. В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает Закон Ома для полной цепи: , (2) где: Из закона Ома для полной цепи вытекают следствия: Часто[2] выражение: (3) (где есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома». Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется: (4) То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС. К другой записи формулы (3), а именно: (5) Применима другая формулировка: Выражение (5) можно переписать в виде: (6) где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный Ом» — Mо[3], впоследствии переименованный в Си́менс (обозначение: См, S). В соответствии с этой диаграммой формально может быть записано выражение: (7) Которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно. В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника: (8) где: Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи = , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач). В таком случае потери мощности будут определяться выражением: = (9) Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт. Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: где: Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является тензором ранга (1, 1). Раздел физики, изучающий течение электрического тока в различных средах, называется электродинамикой сплошных сред. Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига. Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: где: При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждать вольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда. Закон Ома можно просто объяснить при помощи теории Друде: Здесь: dic.academic.ru Закон Ома для участка цепи — самый пожалуй применяемый закон в электронике и электротехнике. За сложностью его формулировки кроется простота и изящество его применения. Формулируется он так: величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению: Запомнить эту формулу очень легко, но если все-же не получается — изготовьте на картоне такой вот треугольничек, как на рисунке в начале статьи. Это волшебный треугольник закона Ома — достаточно закрыть ту величину, которую необходимо найти и оставшаяся часть треугольника покажет формулу нахождения. например, мы знаем напряжение работы лампочки и ее рабочий ток (на лампочках для фонариков они указываются прямо на цоколе). Каково же сопротивление нити накаливания этой лампочки? Все очень просто, закрываем сопротивление в треугольнике и видим, что остается напряжение деленное на ток. А теперь давайте разберемся, что же это все-таки значат все эти мудреные слова в определении. Итак два интересных труднопроизносимых слова, точнее словосочетания: прямо пропорциональна и обратно пропорциональна. Что же значит «величина тока прямо пропорциональна напряжению»? А это значит, что при увеличении напряжения на участке цепи, увеличивается и сила тока в этом участке. То есть, чем больше напряжение, тем больше ток. Это все справедливо для участка цепи с одним и тем же напряжением. Что касается «обратно пропорциональна его сопротивлению», то здесь все наоборот. Чем больше сопротивление участка цепи, тем меньше будет по нему течь ток. Это справедливо в том случае, если к этому участку приложено одно и то же сопротивление. Давайте рассмотрим применение этого закона на простом примере. Возьмем обыкновенный фонарик с лампой накаливания, в который вставляются три «круглых» батарейки. Схема такого фонарика будет выглядеть следующим образом. Электрическая схема фонаря В этой схеме GB1 — GB3 — это три батарейки, S1 — выключатель, HL1 — лампочка. Итак, как нам говорит закон Ома: величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению. Берем для рассмотрения участок цепи, состоящий их лампочки. Теперь простой вопрос: от чего зависит яркость горения лампочки? Правильно — от силы тока, проходящего через нить накаливания этой лампочки. То есть яркость свечения лампочки мы можем использовать как показатель силы тока в цепи фонарика. И действительно, что будет со свечением лампочки если мы уберем одну батарейку и вместо нее вставим перемычку? «Это и ежу понятно. Она будет гореть тусклее!» — скажите Вы. И будете правы. Вот Вам и демонстрация фразы: «величина тока на участке цепи прямо пропорциональна напряжению». Чем больше батареек мы подключим (то есть чем большее напряжение приложим) к одной и той же лампочке, тем ярче она будет гореть (тем больший ток по ней протекает). lightelectronics.ru Материал из свободной русской энциклопедии «Традиция» Зако́н О́ма — закон, который открывает, что ток через проводник между двумя точками прямо пропорционален разности потенциалов между двумя точками. Вводя коэффициент пропорциональности, сопротивление,[1] приходим к обычному математическому уравнению, описывающего эту связь:[2] $$I = \frac{V}{R},$$ где: Закон был назван в честь немецкого физика Георга Ома, который в трактате, опубликованном в 1827 году, описано измерения напряжения и тока с помощью простых электрических цепей, содержащих различные длины провода. Он представил несколько более сложные уравнения, чтобы объяснить его экспериментальные результаты. Приведенное выше уравнение является современной формой закона Ома. В физике термин «закон Ома» также применяется для обозначения различных обобщений закона, первоначально сформулированного Омом. Самый простой пример это: $$\mathbf{J} = \sigma \mathbf{E},$$ где: Эта переформулировка закона Ома принадлежит Густаву Кирхгофу.[4]. В соответствии с этой диаграммой формально может быть записано выражение: \(R\!= {U \over I}, \qquad(7)\) которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно. В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника: \(R\!= {\varrho l \over s}, \qquad(8) \) где: Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока \(P\!\) = \( {\varepsilon\! I\!} \) при минимальных потерях мощности в линии передачи \(P (r)\!\) = \( UI \) , где \(U\! = Ir \), причём \(r\!\) на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач). В таком случае потери мощности будут определяться выражением: \(P(r) = \frac{P^2 r}{\varepsilon ^2}. \qquad(9) \) Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт. Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение. Сопротивление \(R\!\) зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем: $$\mathbf{j} = \sigma \mathbf{E}$$ где: Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость \(\sigma_{ij}\) является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид: $$j_i = \sum_{i=1}^3\sigma_{ij}E_j.$$ Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред. Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновремённости достижения напряжением и током своих максимальных значений, то есть учёта фазового сдвига. Если ток является синусоидальным с циклической частотой \(\omega\), а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: $$\mathbb{U} = \mathbb{I} \cdot Z$$ где: При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, \(U=U_0\sin(\omega t+\varphi)\) подбором такой \(\mathbb{U}=U_0e^{i(\omega t + \varphi)},\) что \(\operatorname{Im} \mathbb{U} = U. \) Тогда все значения токов и напряжений в схеме надо считать как \(F=\operatorname{Im} \mathbb{F}\) Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций. В классическом приближении закон Ома можно вывести при помощи теории Друде: $$\vec j=\frac{n \cdot e_0^{2}\cdot\tau}{m} \cdot\vec E=\sigma\cdot\vec E$$ Здесь: Проводники и элементы, для которых соблюдается закон Ома, называются омическими. Закон Ома может не соблюдаться: traditio.wikiЗакон Ома — проще некуда! Закон ома формулировка
Закон Ома
Закон Ома












Смотрите также
Закон Ома — Википедия
 U — напряжение,I — сила тока,R — сопротивление.
U — напряжение,I — сила тока,R — сопротивление. 
 , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1].
, l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r[1]. 

 есть напряжение, или падение напряжения (или, что то же, разность потенциалов между началом и концом участка проводника), тоже называют «Законом Ома».
есть напряжение, или падение напряжения (или, что то же, разность потенциалов между началом и концом участка проводника), тоже называют «Законом Ома». 


Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. 

Мнемоническая диаграмма для Закона[править]
Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления 

 — удельное электрическое сопротивление материала, из которого сделан проводник,
— удельное электрическое сопротивление материала, из которого сделан проводник, — его длина
— его длина — площадь его поперечного сечения
— площадь его поперечного сеченияЗакон Ома и ЛЭП[править]
 =
=  при минимальных потерях мощности в линии передачи
при минимальных потерях мощности в линии передачи  =
=  , где
, где  , причём
, причём  на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).
на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач). 
Закон Ома в дифференциальной форме[править]
 зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.
зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника. 
 является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид:
является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид: 
Закон Ома для переменного тока[править]
 , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: 
 подбором такой
подбором такой  что
что  Тогда все значения токов и напряжений в схеме надо считать как
Тогда все значения токов и напряжений в схеме надо считать как 
Трактовка и пределы применимости закона Ома[править]

Закон Ома - это... Что такое Закон Ома?
V — напряжение,I — сила тока,R — сопротивление. Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. Мнемоническая диаграмма для Закона
Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления Закон Ома и ЛЭП
Закон Ома в дифференциальной форме
Закон Ома для переменного тока
Трактовка закона Ома
См. также
Примечания
Ссылки
Закон Ома | Онлайн журнал электрика

Простая электронная цепь неизменного тока. 

Дополнительный резистор, включенный в цепь, ограничивает ток в этой цепи. 
Регулирование тока в цепи при помощи переменного резистора. 
Регулирование напряжения на нагрузке R2 при помощи переменного резистора включенного в электронную цепь потенциометром. Закон Ома - это... Что такое Закон Ома?
V — напряжение,I — сила тока,R — сопротивление. Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. Мнемоническая диаграмма для Закона
Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления Закон Ома и ЛЭП
Закон Ома в дифференциальной форме
Закон Ома для переменного тока
Трактовка закона Ома
См. также
Примечания
Ссылки
закон ома для начинающих | Простая электроника
Закон Ома — Традиция
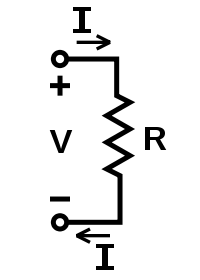 V — напряжение,I — сила тока,R — сопротивление.
V — напряжение,I — сила тока,R — сопротивление.  Георг Симон Ом.
Георг Симон Ом. Мнемоническая диаграмма для Закона[править]
Схема, иллюстрирующая три составляющие закона Ома Диаграмма, помогающая запомнить закон Ома. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления Закон Ома и ЛЭП[править]
Закон Ома в дифференциальной форме[править]
Закон Ома для переменного тока[править]
Трактовка и пределы применимости закона Ома[править]
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''





Поделиться с друзьями: