Содержание
суть явления, закон Фарадея, формулы
Электромагнитная индукция — это очень важное физическое явление, используемое в работе многих устройств, таких как трансформатор, генератор переменного напряжения, индукционная плита. Оно также имело большое теоретическое значение — привело к открытию электромагнитной волны.
Фарадея, первооткрывателя явления электромагнитной индукции, посетил в своей лаборатории министр финансов Великобритании и спросил:
- » Какую пользу человечество получит от вашего исследования? «
Фарадей ответил:
- » Трудно судить, но я уверен, что вы будете собирать с этого налоги. «
Он не ошибся — НДС в той же Великобритании добавляется к цене электроэнергии, поставляемой в дом.
Приведенный выше список применений, хотя и неполный, впечатляет. Они, безусловно, присутствуют в нашей жизни и являются инженерными разработками явления электромагнитной индукции.
В чем заключается явление электромагнитной индукции?
В общем смысле явление электромагнитное индукции заключается в генерации электрического тока с помощью магнитного поля.
Скажем точнее, явление электромагнитной индукции заключается в образовании электродвижущей силы (ЭДС) в проводнике в результате изменения потока магнитного поля, пронизывающего поверхность, охватывающую проводник. В замкнутой цепи электродвижущая сила (ЭДС) вызывает протекание электрического тока.
В приведенном выше определении явления могут быть неясными два понятия — ЭДС индукции и магнитный поток.
ЭДС индукции.
Абсолютная величина электродвижущей силы ( ЭДС индукции с символом εинд ) есть работа внешней силы Az, которая вызывает перемещение единичного заряда по цепи. Следовательно: | εинд | = Az / q .
Как видите, в определении мы использовали абсолютное значение ЭДС индукции. Это потому, что оно может быть отрицательным, при определенных ситуациях. С другой стороны, работа внешних сил, согласно принципу сохранения энергии, всегда, при генерации электрического тока, должна быть положительной.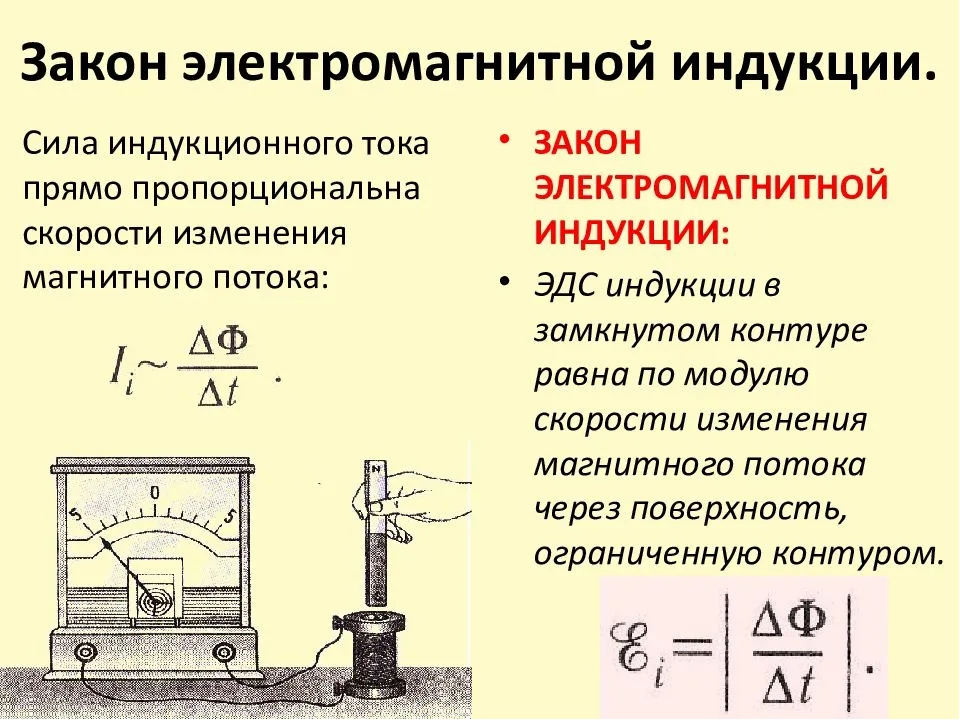
Определение потока магнитной индукции.
Поток магнитной индукции B через поверхность S называется скалярным произведением векторов B и S: dФ = B * S * cos α , где α — угол между двумя векторами, а S — вектор, перпендикулярный поверхности S с величиной, равной площади этой поверхности.
Магнитный поток будет меняться при изменении любой величины, входящей в формулу — площади поверхности, значения магнитной индукции, угла между площадью поверхности и вектором индукции — при сохранении постоянства остальных переменных. Конечно, все эти величины могут изменяться одновременно, но таким образом, что их произведение не остается постоянным.
О том, что электрический ток является источником магнитного поля, было известно с 1820 года (работа Орстеда). Фарадей задался вопросом, не верно ли и обратное — не может ли магнитное поле быть источником (причиной) электрического тока. Однако дело оказалось не таким простым. Только в 1831 году ученый наблюдал это явление при определенных особых обстоятельствах. Оказалось, что при стабильных условиях электрический ток не возникает.
Оказалось, что при стабильных условиях электрический ток не возникает.
Почему это происходит? Даже в очень сильном, но постоянном во времени магнитном поле электрический ток не будет течь в замкнутой цепи «сам по себе». Он течет только тогда, когда мы соответствующим образом перемещаем контур или изменяем магнитное поле, в котором находится контур.
Когда Фарадей обратил внимание на условия, при которых в присутствии магнитного поля возникает электрический ток, он провел десятки экспериментов, которые обобщил и из которых сделал количественные выводы в виде закона электромагнитной индукции. Мы не будем здесь говорить об этом законе, а сосредоточимся только на сути явления электромагнитной индукции. Мы попытаемся увидеть двойственность этого явления, т.е. то, что оно имеет две разновидности, и ответить на вопрос, почему электрический ток течет при определенных условиях.
Мы рассмотрим, какие силы вызывают индукционный ток, т.е. какие силы действуют на свободные заряды в проводнике, заставляя их двигаться.
Эксперимент Фарадея 1831 года, демонстрирующий электромагнитную индукцию между двумя катушками (см. рисунок 1).
Справа находится аккумулятор, питающий меньшую из двух катушек (A), которая создает магнитное поле. Когда эта катушка находится в состоянии покоя, индукционный ток не наблюдается. Однако если переместить его внутрь большей катушки (B), переменный магнитный поток индуцирует в ней ток. Мы обнаруживаем это, наблюдая за колебаниями стрелки гальванометра (G) слева.
Рис. 1. Эксперимент Фарадея 1831 года, демонстрирующий электромагнитную индукцию между двумя катушками (см. рисунок 1). Источник: J. Lambert [Public domain], Wikimedia Commons)
Закон электромагнитной индукции Фарадея
Явление электромагнитной индукции описывается законом Фарадея, первооткрывателя и исследователя этого явления.
Представьте себе простейший контур с подвижной стороной, помещенный в магнитное поле так, чтобы поверхность контура была перпендикулярна линиям магнитного поля (рис. 2.).
2.).
Рис. 2. Контур с подвижной стороной (перекладиной)
Мы перемещаем контур со скоростью v вправо. Это изменяет поток магнитной индукции, пронизывающий поверхность, охватываемую контуром, обозначенным на рисунке более темным цветом.
Вспоминая определение магнитного потока индукции, мы можем понять, почему изменяется поток ФB (рис. 2) — потому что, значение площади S поверхности увеличивается .
Вследствие изменения потока магнитной индукции в рассматриваемой цепи возникнет электродвижущая сила индукции и, следовательно, потечет электрический ток.
Рис. 3. Внешняя сила Fz уравновешивает электродинамическую силу Fed , действующую на контур, движущийся с постоянной скоростью v
В рассматриваемом нами случае легко вычислить работу внешней силы, предполагая постоянную скорость движения контура. Внешняя сила Fz действует в соответствии со смещением контура (и вектором скорости) и в любой момент уравновешивает электродинамическую силу (силу Ампера) Fed, действующую в противоположном направлении (рис. 3.). Согласно определению работы Az = F * Δx где Δx — смещение контура во времени Δt.
3.). Согласно определению работы Az = F * Δx где Δx — смещение контура во времени Δt.
Величина силы Fz равна величине электродинамической силы (силе Ампера) Fed, действующей на контур. Поэтому Az = I * L * B * Δx, где — I сила индукционного тока, протекающего в цепи (и в контуре), L — длина контура (той части, где протекает электрический ток), B — величина магнитной индукции. Давайте введем наше выражение в определение ЭДС индукции. Зная, что q = I * Δt, получаем:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * ΔS / Δt = dФB / dt.
Мы получили интересный результат. Абсолютное значение ЭДС индукции равно скорости изменения потока магнитной индукции.
В рассматриваемом здесь случае поток магнитной индукции изменяется равномерно во времени. В общем случае это совсем не обязательно. Вот почему мы пишем: εинд = ΔФB / Δt , где Δt → 0, который в сокращенном виде записывается как dФB / dt .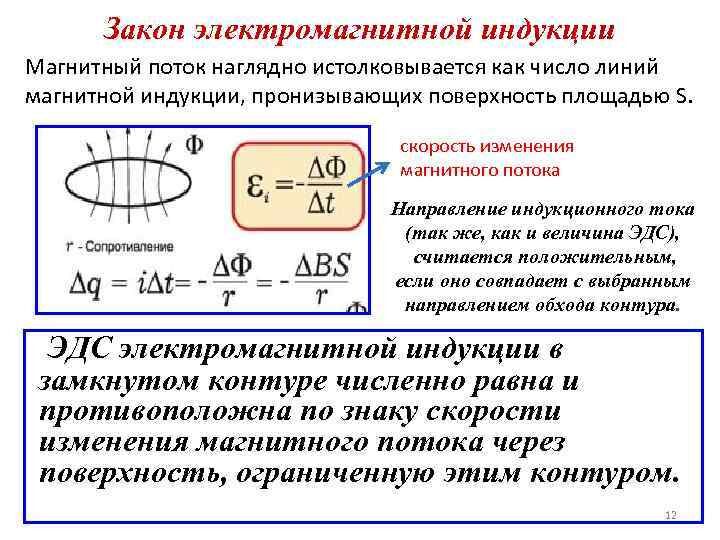 Это производная магнитного потока по времени.
Это производная магнитного потока по времени.
Хотя наш вывод формулы относится к одному примеру, оказывается, что выведенное отношение является общим. Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Таким образом, закон электромагнитной индукции Фарадея записывается следующим образом: εинд = — dФB / dt и формулируется так:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.
Википедия
Знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт отражён в правиле Ленца.
Этот закон верен независимо от того, как изменяется поток магнитного поля; когда изменение вызвано относительным движением источника магнитного поля и контура, или когда движения вообще нет, но значение магнитной индукции меняется.
Закон Фарадея — это универсальный, всеобъемлющий и полный математический отчет о явлении электромагнитной индукции.
Вернемся на мгновение к нашему примеру и отметим, что скорость изменения потока, а значит и абсолютное значение ЭДС индукции, в данном случае равна произведению B*L*v. Это следует из ранее написанных соотношений, а именно:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * L * ( Δx / Δt ) = B * L * v .
Правило Ленца.
Правило Ленца позволяет быстро и легко определить направление индукционного тока. Это действительно одна из форм принципа сохранения энергии. Правило гласит, что индукционный ток, наведенный в проводнике под действием переменного потока магнитной индукции, всегда имеет такое направление, что магнитное поле, создаваемое этим индукционным током, противодействует причине (т.е. изменению потока магнитного поля), которая его вызвала.
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м «втягивается» с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
Рис. 4. Пример задачи по электростатической индукции
Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем — магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т. е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при «втягивании» контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Рис. 5
Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев). На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I — сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .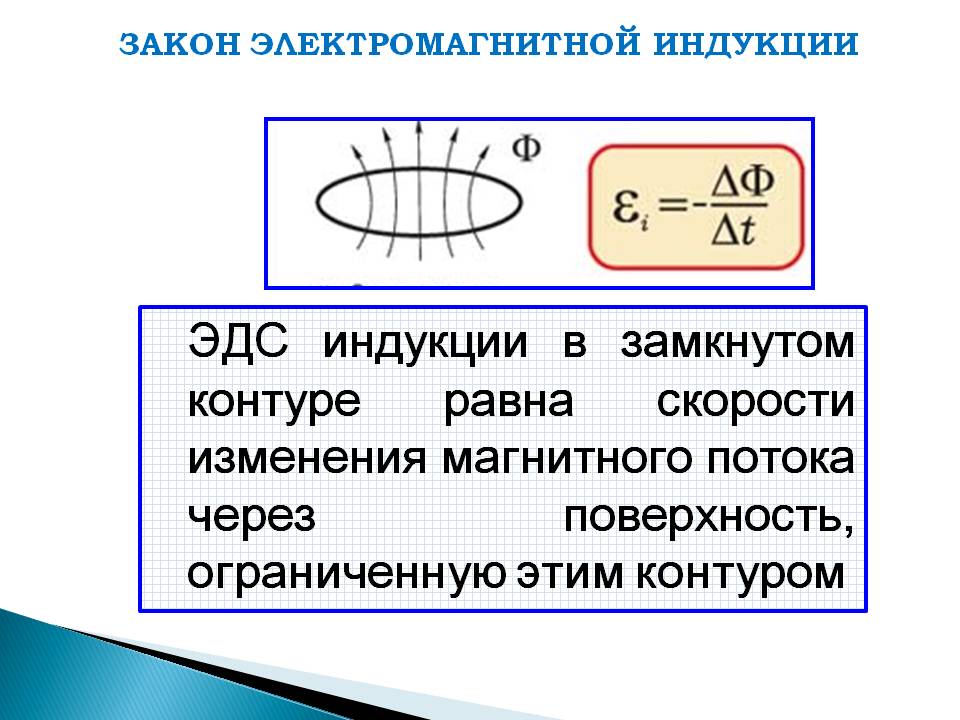
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Список использованной литературы
- Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
- Физика, базовый уровень, 11 класс, учебник — Пурышева Н.С., Важеевская Н.
 Е., Исаев Д.А., Чаругин В.М
Е., Исаев Д.А., Чаругин В.М
Что такое электромагнитная индукция. Закон электромагнитной индукции
История
Около 1830 г. Майкл Фарадей установили, что химические реакции на каждой из двух поверхностей раздела электрод-электролит обеспечивают «место действия ЭДС» для гальванического элемента. То есть эти реакции приводят в движение ток, а не являются бесконечным источником энергии, как предполагалось изначально. [11] В случае разомкнутой цепи разделение зарядов продолжается до тех пор, пока электрическое поле разделенных зарядов не станет достаточным для остановки реакций. Годами ранее, Алессандро Вольта, который измерял контактную разность потенциалов на границе металл – металл (электрод – электрод) своих ячеек, ошибочно полагал, что только контакт (без учета химической реакции) является источником ЭДС.
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.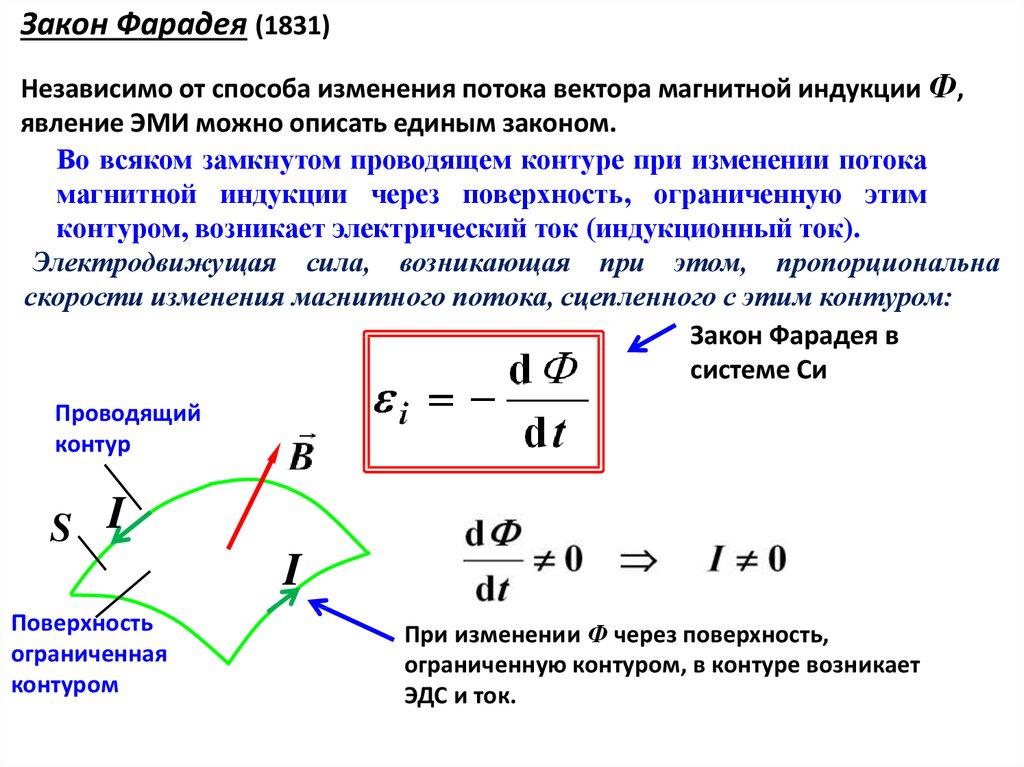
Явление электромагнитной индукции было открыто М. Фарадеем.
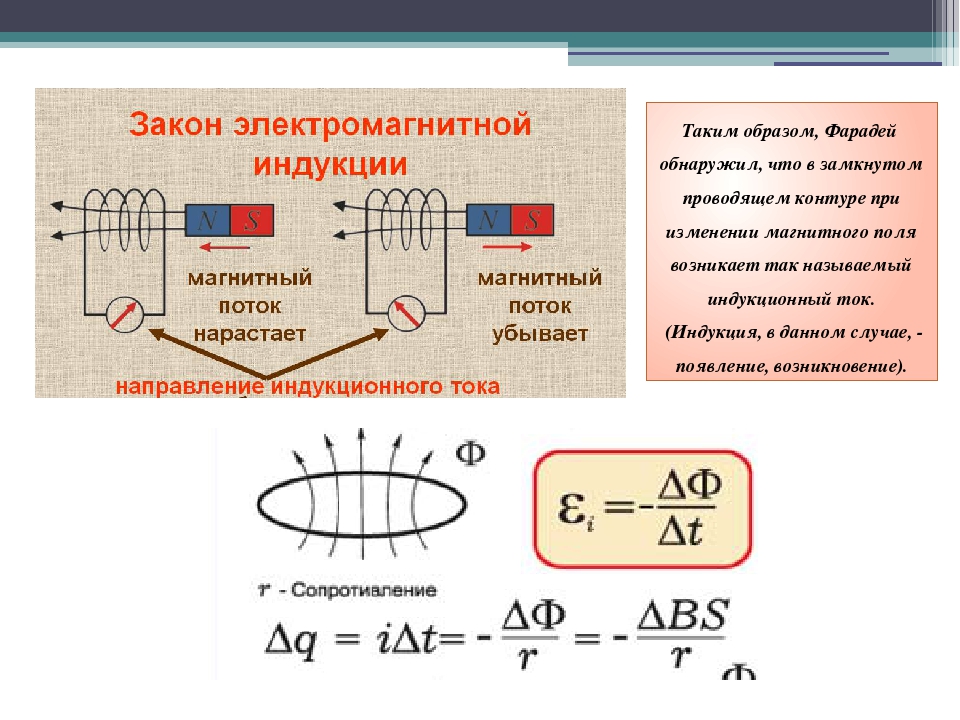
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
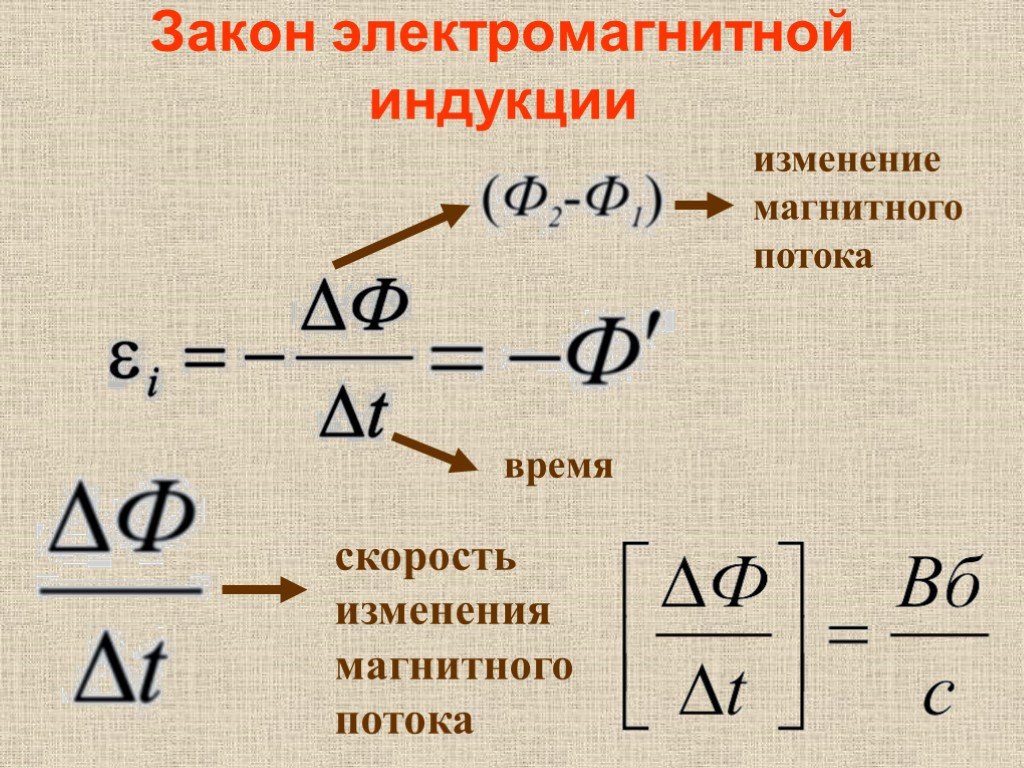
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
| Закон Фарадея
Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] |
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
| Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков [-] |
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
| Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В] I — сила индукционного тока [А] R — сопротивление контура [Ом] |
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
| ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В] B — магнитная индукция [Тл] v — скорость проводника [м/с] l — длина проводника [м] |
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Закон электромагнитной индукции Фарадея
Явление электромагнитной индукции описывается законом Фарадея, первооткрывателя и исследователя этого явления.
Представьте себе простейший контур с подвижной стороной, помещенный в магнитное поле так, чтобы поверхность контура была перпендикулярна линиям магнитного поля (рис. 2.).
2.).
Рис. Контур с подвижной стороной (перекладиной)
Мы перемещаем контур со скоростью v вправо. Это изменяет поток магнитной индукции, пронизывающий поверхность, охватываемую контуром, обозначенным на рисунке более темным цветом.
Вспоминая определение магнитного потока индукции, мы можем понять, почему изменяется поток ФB (рис.) – потому что, значение площади S поверхности увеличивается .
Вследствие изменения потока магнитной индукции в рассматриваемой цепи возникнет электродвижущая сила индукции и, следовательно, потечет электрический ток.
Рис. Внешняя сила Fz уравновешивает электродинамическую силу Fed , действующую на контур, движущийся с постоянной скоростью v
В рассматриваемом нами случае легко вычислить работу внешней силы, предполагая постоянную скорость движения контура. Внешняя сила Fz действует в соответствии со смещением контура (и вектором скорости) и в любой момент уравновешивает электродинамическую силу (силу Ампера) Fed, действующую в противоположном направлении (рис. 3.). Согласно определению работы Az = F * Δx где Δx – смещение контура во времени Δt.
3.). Согласно определению работы Az = F * Δx где Δx – смещение контура во времени Δt.
Величина силы Fz равна величине электродинамической силы (силе Ампера) Fed, действующей на контур. Поэтому Az = I * L * B * Δx, где – I сила индукционного тока, протекающего в цепи (и в контуре), L – длина контура (той части, где протекает электрический ток), B – величина магнитной индукции. Давайте введем наше выражение в определение ЭДС индукции. Зная, что q = I * Δt, получаем:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * ΔS / Δt = dФB / dt.
Мы получили интересный результат. Абсолютное значение ЭДС индукции равно скорости изменения потока магнитной индукции.
В рассматриваемом здесь случае поток магнитной индукции изменяется равномерно во времени. В общем случае это совсем не обязательно. Вот почему мы пишем: εинд = ΔФB / Δt , где Δt → 0, который в сокращенном виде записывается как dФB / dt . Это производная магнитного потока по времени.
Хотя наш вывод формулы относится к одному примеру, оказывается, что выведенное отношение является общим.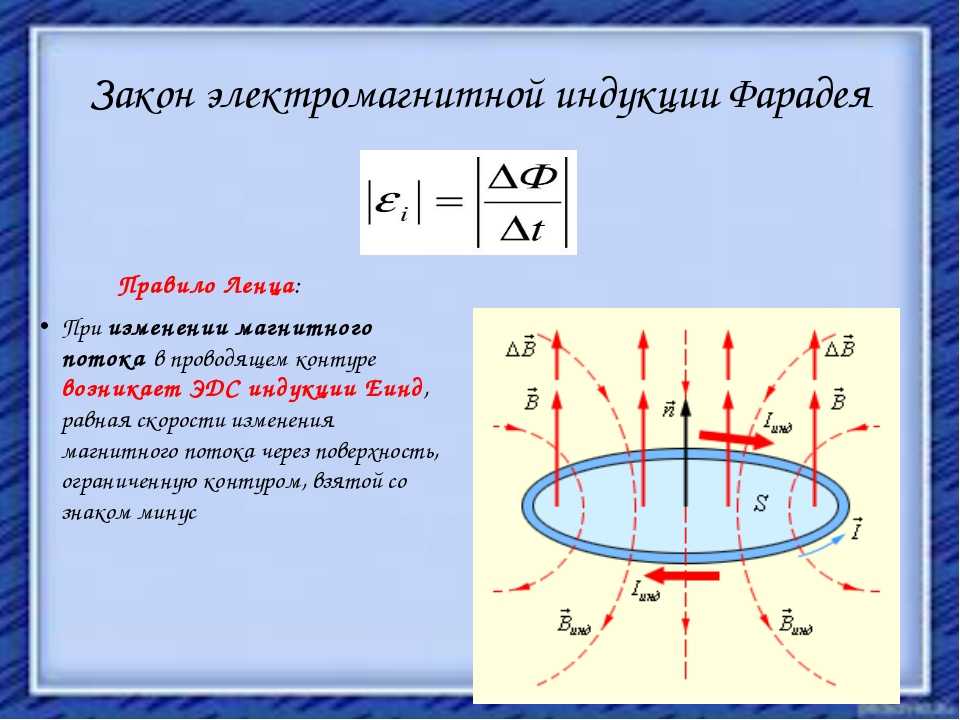 Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Таким образом, закон электромагнитной индукции Фарадея записывается следующим образом: εинд = – dФB / dt и формулируется так:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.
Знак “минус” означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт отражён в правиле Ленца.
Этот закон верен независимо от того, как изменяется поток магнитного поля; когда изменение вызвано относительным движением источника магнитного поля и контура, или когда движения вообще нет, но значение магнитной индукции меняется.
Закон Фарадея – это универсальный, всеобъемлющий и полный математический отчет о явлении электромагнитной индукции.
Вернемся на мгновение к нашему примеру и отметим, что скорость изменения потока, а значит и абсолютное значение ЭДС индукции, в данном случае равна произведению B*L*v. Это следует из ранее написанных соотношений, а именно:
Это следует из ранее написанных соотношений, а именно:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * L * ( Δx / Δt ) = B * L * v .
Правило Ленца.
Правило Ленца позволяет быстро и легко определить направление индукционного тока. Это действительно одна из форм принципа сохранения энергии. Правило гласит, что индукционный ток, наведенный в проводнике под действием переменного потока магнитной индукции, всегда имеет такое направление, что магнитное поле, создаваемое этим индукционным током, противодействует причине (т.е. изменению потока магнитного поля), которая его вызвала.
Обозначение и единицы измерения
Вектор магнитной индукции: формула
ЭДС в формулах обозначают вектором Е. Подразумевается напряженность, которую создают сторонние силы. Соответствующим образом эту величину можно оценивать по разнице потенциалов. По действующим международным стандартам (СИ), единица измерения – один вольт. Большие и малые значения указывают с применением кратных приставок: «микро», «кило» и др.
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.
Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн.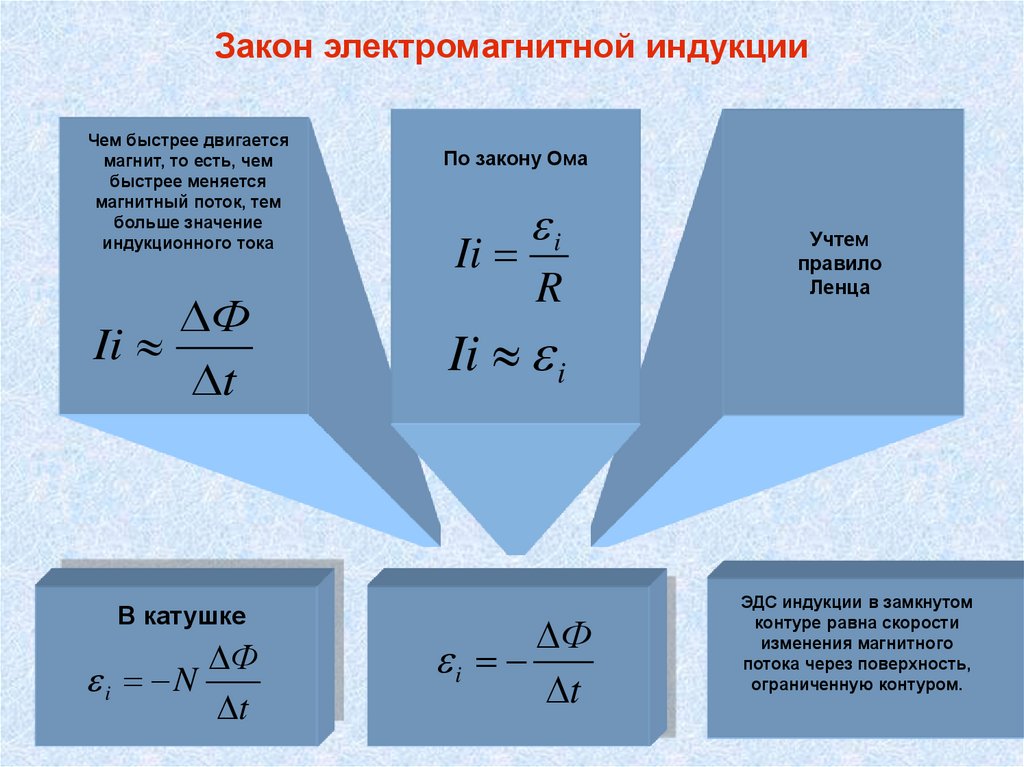 Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Где используются разные виды ЭДС
Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.
Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле.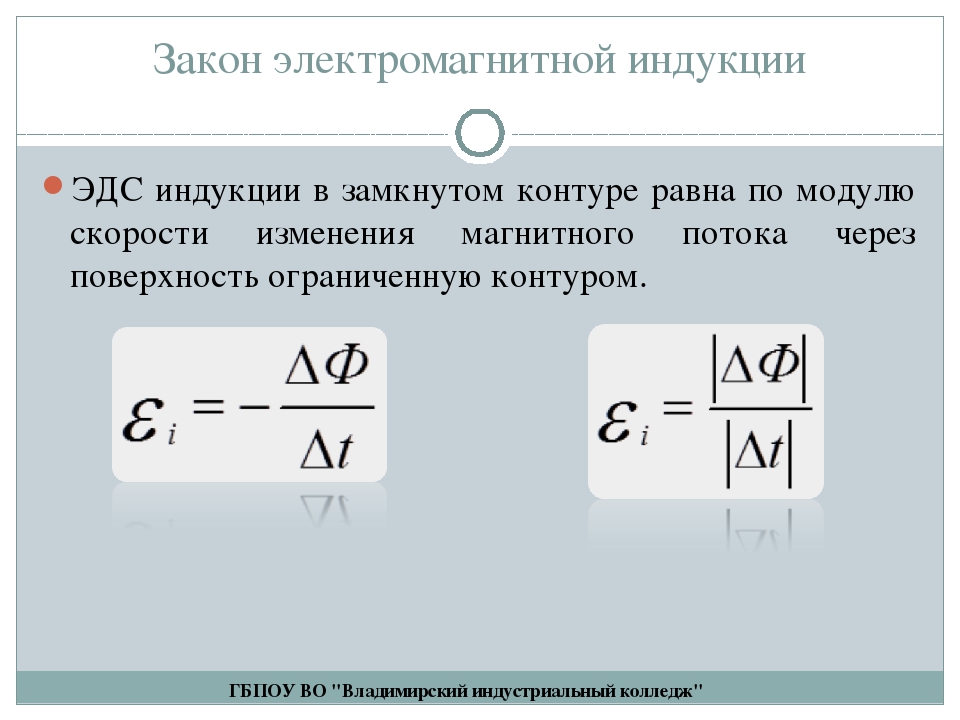 Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора. Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора.
Рис. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис).
Рис. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м “втягивается” с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
Рис. . Пример задачи по электростатической индукции
Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем – магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т.е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при “втягивании” контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.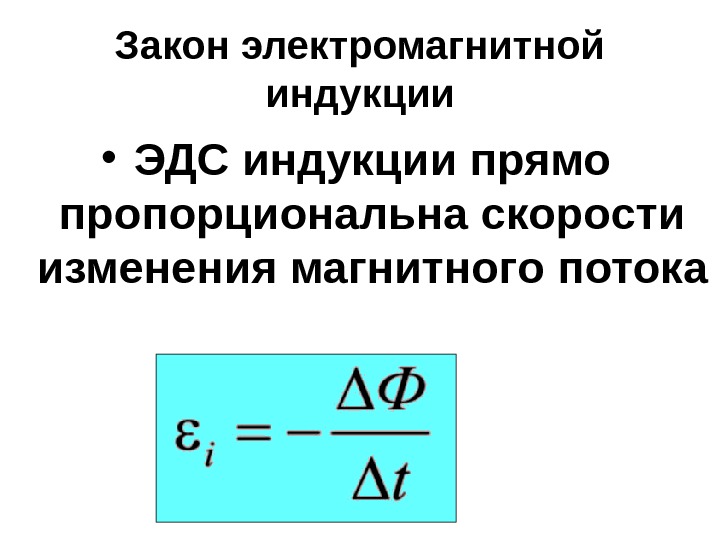
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Рис.
Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев). На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I – сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Что мы узнали?
Кратко и понятно явление электромагнитной индукции можно описать, как возникновение электрического тока в проводящем контуре при изменении магнитного потока, проходящего через этот контур. При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
При этом возникающий ток направлен так, чтобы противодействовать причине, его создавшей.
Источники
- https://wikibgu.ru/wiki/Electromotive_Force
- https://fizi4ka.ru/egje-2018-po-fizike/jelektromagnitnaja-indukcija.html
- https://skysmart.ru/articles/physics/zakon-elektromagnitnoj-indukcii
- https://www.asutpp.ru/elektromagnitnaya-induktsiya.html
- https://amperof.ru/teoriya/formula-eds-indukcii.html
- https://odinelectric.ru/knowledgebase/chto-takoe-eds-induktsii-i-kogda-voznikaet
- https://ege-study.ru/ru/ege/materialy/fizika/elektromagnitnaya-indukciya/
- https://obrazovaka.ru/fizika/elektromagnitnaya-indukciya-formula.html
Как вам статья?
Павел
Бакалавр «210400 Радиотехника» – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
13.S: Электромагнитная индукция (Резюме) — Physics LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10307
- OpenStax
- OpenStax
Основные термины
| обратная ЭДС | ЭДС, создаваемая работающим двигателем, поскольку состоит из катушки, вращающейся в магнитном поле; он противостоит напряжению, питающему двигатель |
| вихретоковый | токовая петля в проводнике, вызванная ЭДС движения |
| электрогенератор | устройство для преобразования механической работы в электрическую энергию; он индуцирует ЭДС, вращая катушку в магнитном поле |
| Закон Фарадея | ЭДС индукции создается в замкнутом контуре за счет изменения магнитного потока через контур |
| индуцированное электрическое поле | создан на основе изменения магнитного потока во времени |
| ЭДС индукции | кратковременное напряжение, создаваемое проводником или катушкой, движущейся в магнитном поле |
| Закон Ленца | направление ЭДС индукции противоположно изменению магнитного потока, вызвавшего ее; это отрицательный знак в законе Фарадея |
| магнитное демпфирование | сопротивление, создаваемое вихревыми токами |
| магнитный поток | измерение количества силовых линий магнитного поля, проходящих через заданную площадь |
| ЭДС индукции движения | напряжение, создаваемое движением проводника в магнитном поле |
| пиковая ЭДС | максимальная ЭДС, создаваемая генератором |
Ключевые уравнения
| Магнитный поток | \(\displaystyle Φ_m=∫_S\vec{B}⋅\шляпа{n}dA\) |
| Закон Фарадея | \(\displaystyle ε=-N\frac{dΦ_m}{dt}\) |
| ЭДС индукции движения | \(\displaystyle ε=Blv\) |
| ЭДС движения вокруг цепи | \(\displaystyle ε=∮\vec{E}⋅d\vec{l}=-\frac{dΦ_m}{dt}\) |
| ЭДС, создаваемая электрическим генератором | \ (\ Displaystyle ε = NBAωsin (ωt) \) |
Резюме 92\).
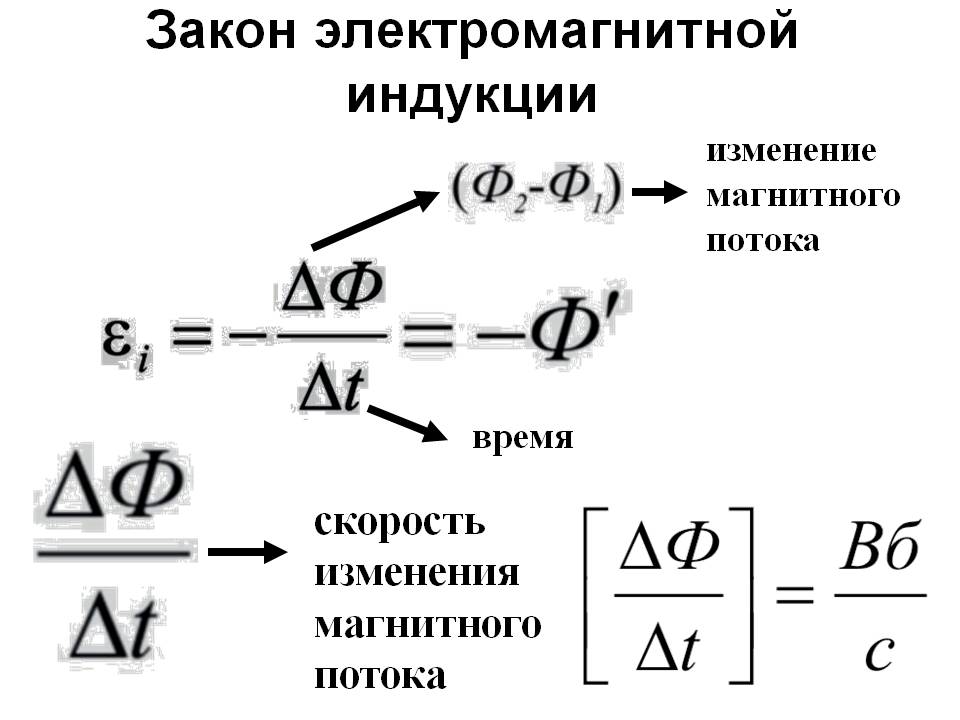
13.3 Закон Ленца
- Закон Ленца можно использовать для определения направлений индуцированных магнитных полей, токов и ЭДС.
- Направление ЭДС индукции всегда противоположно изменению магнитного потока, которое вызывает ЭДС, результат, известный как закон Ленца.
13.4 ЭДС движения
- Связь между ЭДС индукции εε в проводе, движущемся с постоянной скоростью v через магнитное поле B , определяется как \(\displaystyle ε=Blv\).
- ЭДС индукции по закону Фарадея создается ЭДС движения, противодействующей изменению потока.
13.5 Наведенные электрические поля
- Изменяющийся магнитный поток индуцирует электрическое поле.
- И изменяющийся магнитный поток, и индуцированное электрическое поле связаны с индуцированной ЭДС из закона Фарадея.

13.6 Вихревые токи
- Токовые петли, возникающие в движущихся проводниках, называются вихревыми токами. Они могут создавать значительное сопротивление, называемое магнитным демпфированием.
- Манипуляции с вихревыми токами нашли применение в таких устройствах, как металлодетекторы, тормоза в поездах или американских горках, а также индукционные варочные панели.
13.7 Электрические генераторы и обратная ЭДС
- Электрический генератор вращает катушку в магнитном поле, индуцируя ЭДС, определяемую как функция времени \(\displaystyle ε=NBAωsin(ωt)\), где A — это площадь N -витковой катушки, вращающейся с постоянной угловой скоростью \(\displaystyle ω\) в однородном магнитном поле \(\displaystyle \vec{B}\).
- Пиковая ЭДС генератора равна \(\displaystyle ε_0=NBAω\).
- Любая вращающаяся катушка производит ЭДС индукции. В двигателях это называется обратной ЭДС, потому что она противодействует входу ЭДС в двигатель.

13.8 Применение электромагнитной индукции
- Жесткие диски используют магнитную индукцию для чтения/записи информации.
- Другие применения магнитной индукции можно найти в графических планшетах, электрических и гибридных транспортных средствах, а также в транскраниальной магнитной стимуляции.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Эта страница под названием 13.S: Электромагнитная индукция (резюме) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
-
- Теги
-
- source@https://openstax.
 org/details/books/university-physics-volume-2
org/details/books/university-physics-volume-2
- source@https://openstax.
Закон Фарадея – формула и пример
Вы находите понятие электромагнитной индукции (ЭМП) сложным? Это может быть потому, что вы сами не понимаете своих основ. Чтобы понять EMI, вам сначала нужно понять концепцию законов Фарадея об EMI. Эти законы были постулированы одним из величайших физиков всех времен — Майклом Фарадеем. Овладение этими законами облегчит вам понимание EMI.
Прежде чем мы поймем закон Фарадея, давайте сначала поймем, что такое электромагнитная индукция.
Электромагнитная индукция — это явление, которое индуцирует ток в цепи. Это происходит из-за изменения магнитного поля. Ток в проводе возникает из-за движения провода в магнитном поле или изменения силы магнитного поля с течением времени. Обе эти ситуации могут привести к протеканию тока в проводе.
Электродвижущая сила рассматривается как количество энергии, которое вызывает протекание тока по цепи. Электродвижущая сила, возникающая в проводе за счет изменения величины тока в связанной катушке, называется взаимной индуктивностью.
Электродвижущая сила, возникающая в проводе за счет изменения величины тока в связанной катушке, называется взаимной индуктивностью.
Закон Фарадея – формула и пример
Закон Фарадея электромагнитной индукции, также называемый законом электромагнетизма. Этот закон объясняет принцип действия электрических генераторов, электрических индукторов, электрических трансформаторов и электрических двигателей. Это помогает понять важные моменты, которые приводят к электромагнитной индукции или производству электричества. Закон Фарадея используется, чтобы увидеть, как магнитные поля меняются из-за протекания тока в проводах.
Этот закон был впервые сформулирован в 1831 году химиком и физиком «Майкл Фарадей». Благодаря ему закон получил свое название. Закон Фарадея является результатом наблюдений за тремя основными экспериментами, которые он провел. Благодаря этим экспериментам он открыл принцип электромагнитной индукции.
Первый закон Фарадея
(Изображение скоро будет загружено)
Первый закон электромагнитной индукции Фарадея объясняет, что, когда провод находится в поле, которое испытывает постоянное изменение его магнитного поля, возникает электромагнитное поле. Это явление развития электромагнитного поля называется ЭДС индукции. Если это замкнутая цепь, то внутри цепи также индуцируется ток. Он называется «Индуцированный ток».
Это явление развития электромагнитного поля называется ЭДС индукции. Если это замкнутая цепь, то внутри цепи также индуцируется ток. Он называется «Индуцированный ток».
Способы изменения магнитного поля
Существует четыре способа изменения магнитного поля в цепи.
-
Поворотом катушки относительно магнита.
-
Путем перемещения катушки в магнитное поле или вне магнитного поля.
-
Путем изменения области катушки, находящейся в магнитном поле.
-
Движением магнита в направлении катушки или против направления катушки.
Второй закон Фарадея
Теперь давайте разберемся со вторым законом Фарадея. Это еще один закон Фарадея об электромагнитной индукции. Закон объясняет, что ЭДС, индуцированная в проводнике, эквивалентна скорости, с которой поток связан с изменениями цепи. Здесь этот поток является произведением потока в проводе и количества витков в проводе.
Это еще один закон Фарадея об электромагнитной индукции. Закон объясняет, что ЭДС, индуцированная в проводнике, эквивалентна скорости, с которой поток связан с изменениями цепи. Здесь этот поток является произведением потока в проводе и количества витков в проводе.
Формула закона Фарадея
Давайте посмотрим, как был установлен закон Фарадея. Давайте сначала разберемся с терминами:
Где,
\[\epsilon\] = ЭДС или электродвижущая сила
\[\phi\] = магнитный поток
Н = общее число витков в катушке
Скорость, с которой изменения потока в цепи равны величине электродвижущей силы (ε), развиваемой в цепи. Приведенное выше утверждение можно записать в виде следующего уравнения:
\[\epsilon = \frac{dt}{d \Phi}\]
Электродвижущая сила или ЭДС представляет собой разность потенциалов, возникающих в «ненагруженном контуре». . Это происходит, когда сопротивление, присутствующее в цепи, достигает высокого уровня. Как ЭДС, так и напряжение, оба измеряются в напряжении, поэтому ЭДС также можно рассматривать как напряжение.
. Это происходит, когда сопротивление, присутствующее в цепи, достигает высокого уровня. Как ЭДС, так и напряжение, оба измеряются в напряжении, поэтому ЭДС также можно рассматривать как напряжение.
Существует еще один важный закон, описывающий электродвижущую силу, например, закон Фарадея.
Закон Ленца был постулирован в 1833 году Генрихом Ленцем. Если закон Фарадея описывает величину ЭДС, генерируемой внутри цепи, то закон Ленца говорит о направлении тока в цепи. Закон объясняет, что направление тока будет противоположно направлению вызвавшего его потока. Другими словами, направление любого магнитного поля, создаваемого «индуцированным током», противоположно изменению в реальном поле.
Закон Ленца приводит к тому же выводу, что и закон Фарадея. Отличие только в знаке минус «-». Этот отрицательный знак указывает на то, что направление магнитного поля и направление ЭДС индукции имеют противоположные знаки.
\[\epsilon = -\frac{dt}{d \phi}\]
Если в катушке N витков, то полная магнитная индукция в катушке представляется как \[\epsilon = — N \frac{dt}{d \phi}\]
Эксперимент Фарадея
Взаимосвязь между ЭДС индукции и магнитным потоком:
(Изображение скоро будет загружено)
В первом законе Фарадея было сказано, что когда изменяется общая напряженность магнитного поля, то только оно индуцирует ток в цепи. Это было доказано подключением амперметра к проволочной петле. Этот амперметр отклоняется при движении магнита в направлении провода.
Это было доказано подключением амперметра к проволочной петле. Этот амперметр отклоняется при движении магнита в направлении провода.
Во втором эксперименте Фарадея было установлено, что когда ток проходит через железный стержень, он делает его электромагнитным. Он также заметил, что из-за относительного движения между катушкой и магнитом возникает индуцированная электромагнитная сила.
-
Когда магнит вращается вокруг оси, ЭДС не возникает, а когда магнит вращается вокруг своей оси, возникает ЭДС индукции. Когда магнит неподвижен или закреплен на своем месте, то в амперметре не наблюдается отклонения.
-
Когда магнит приближается к катушке, измеряемое напряжение достигает своего пика.
-
Когда магнит удаляется от провода, величина генерируемого напряжения направлена в противоположную сторону контура.

Третий эксперимент был проведен и записан. В этом эксперименте, когда катушка была неподвижна, она не вызывала отклонения в гальванометре. Таким образом, в катушке генерировался наведенный ток. Но, когда магнит удалялся далеко от цепи, то амперметр показывал отклонение в сторону от петли.
Применение закона Фарадея
Ниже приведены некоторые важные примеры использования закона Фарадея:
-
Трансформаторы и другие электронные устройства работают по принципу закона Фарадея.
-
Индукционная плита также работает по принципу взаимной индукции, который, в свою очередь, основан на законе Фарадея.
-
Наведение ЭДС в электромагнитном расходомере помогает регистрировать скорость потока жидкости.
-
Законы Фарадея также применяются во многих медицинских устройствах, таких как МРТ, рентгеновские аппараты, компьютерная томография и т.
 д. из-за их широкой области применения, но мало кто говорит об их изобретателе — Майкле Фарадее. Чтобы повысить ваше любопытство к теме, мы включили несколько забавных фактов о нем, а именно:
д. из-за их широкой области применения, но мало кто говорит об их изобретателе — Майкле Фарадее. Чтобы повысить ваше любопытство к теме, мы включили несколько забавных фактов о нем, а именно: -
Он был физиком-самоучкой, потому что в детстве его родители не могли позволить себе формальное образование для него
-
Он известен как «Отец электричества» вместе с Николой Теслой
-
Его законы об электромагнетизме проложил путь для механизированного века
-
В 1820 году он изобрел двигатель с магнитами и ртутью
-
Он впервые продемонстрировал притяжение магнитной силы, для чего он использовал стержневой магнит и железные опилки. Сегодня этот эксперимент проводят многие студенты по всему миру.
-