Соединения резисторов калькулятор: Калькулятор параллельных сопротивлений

Содержание

Соединение резисторов последовательное, параллельное, смешанное. Пример расчета

Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.

Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.

Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.

Последовательное соединение резисторов

Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.

Принципиальная схема последовательного соединения:

Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.

Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:

R = R1 + R2 + R3 + … + Rn.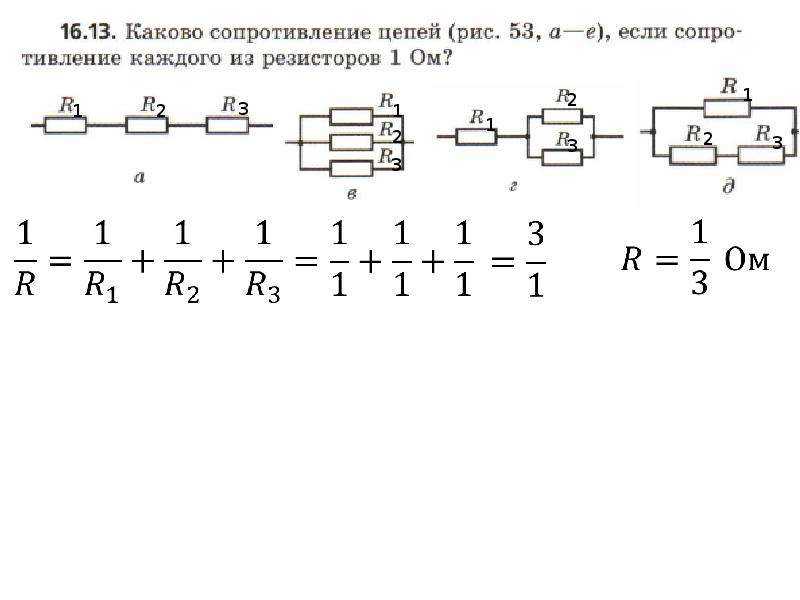

R = 20 + 70 + 10 = 100 Ом.

В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:

I = U / R = U / (R1 + R2 + R3 + … + Rn).

I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.

Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):

U1 = I × R1.
U2 = I × R2.
U3 = I × R3.
Un = I × Rn.

Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).

Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:

Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.

В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.

Объединение резистивных радиокомпонентов

https://youtube.com/watch?v=jJX6IsRhnhs

Параллельное соединение

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

Последовательное и параллельное подключение резисторов. Как рассчитать с помощью формул?

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

Номинал резистора в 16 Ом подойдет.
Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

Калькулятор соединения резисторов онлайн. параллельное соединение резисторов

Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
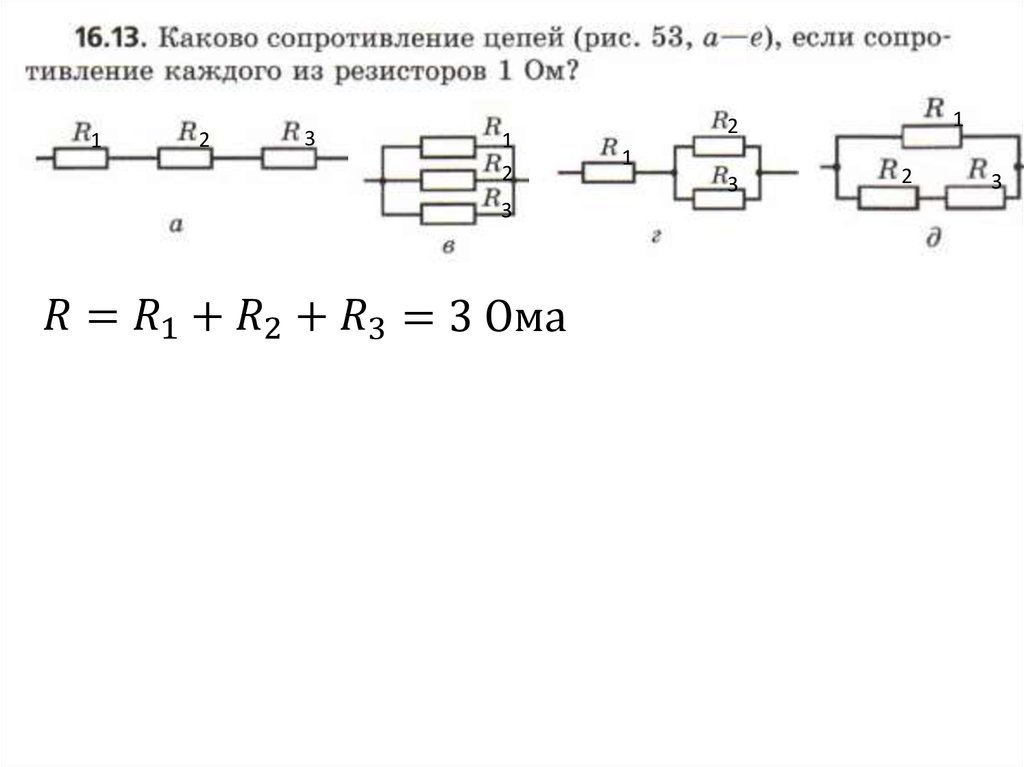
Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

Ток не изменяется на участке цепи.
Общее напряжение равно сумме падений напряжений на каждом резисторе.
Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А.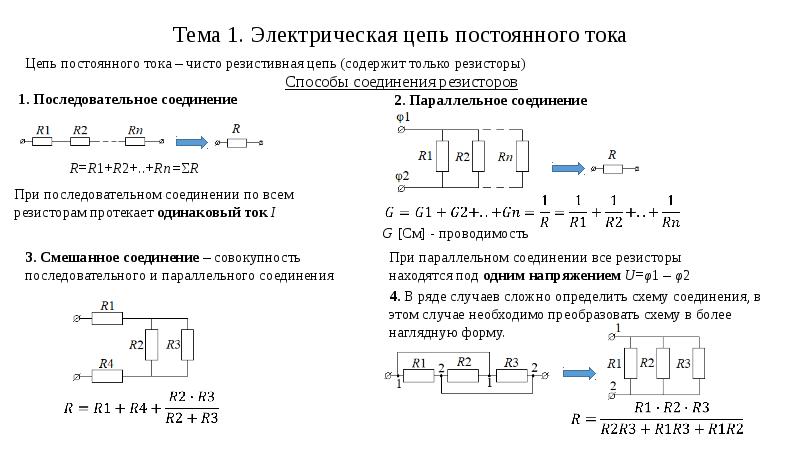 Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

I = I1 = I2 = 0,5 (А).
Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Параллельное соединение резисторов

Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.

При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un.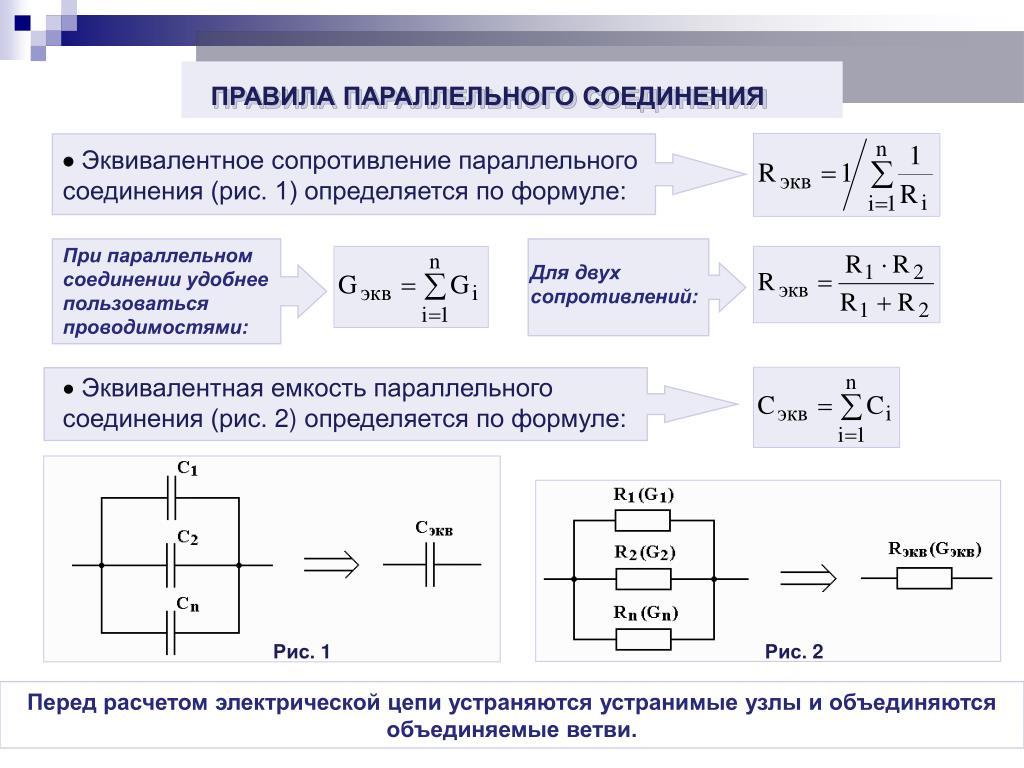 По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:

1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:

1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.

R ≈ 1 / 0,164 ≈ 6,097 Ом.

Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):

Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).

Выделим основные особенности параллельного соединения резисторов:

Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).

Как рассчитать сложные схемы соединения резисторов

Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

Перед нами сложная схема – задача рассчитать общее сопротивление:

R 2, R 3, R 4 объединим в последовательную группу – применим формулу R 2,3,4 = R 2+R 3+ R4.
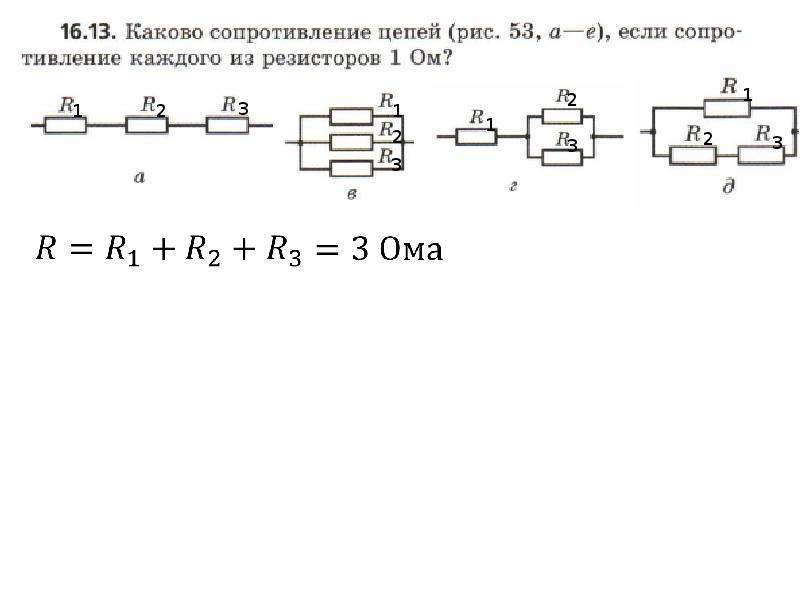
R 5 и R 2,3,4 – параллельно соединенные резисторы, рассчитаем R 5,2,3,4 = 1/ (1/R 5+1/R 2,3,4).
R 5,2,3,4, R 1, R 6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R 5,2,3,4+R 1+R 6.

Смешанное соединение резисторов

Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.

Пример цепи со смешанным соединением резисторов:

Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:

	Определяется общее сопротивление участков с параллельным соединением резисторов.
	Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление.
	После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.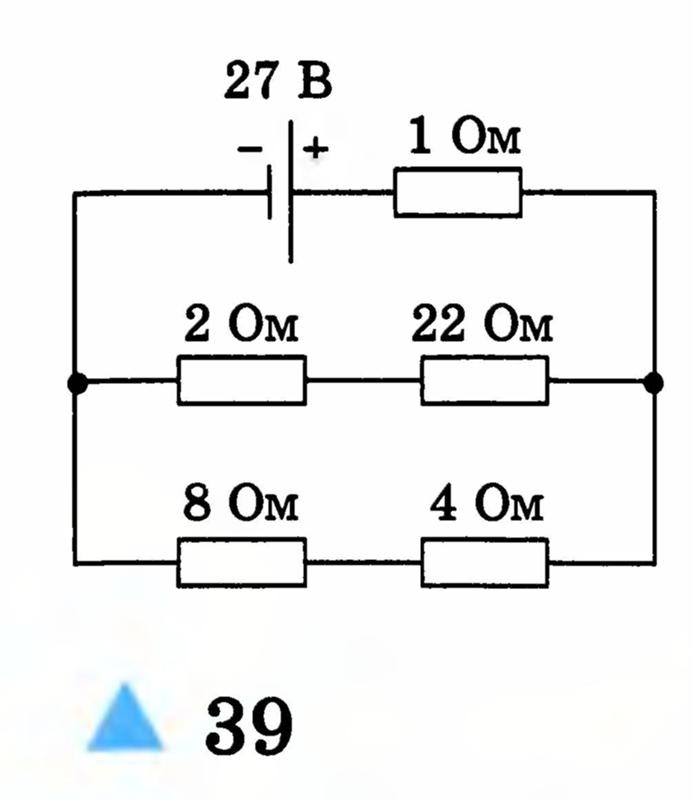
	Далее рассчитывается сопротивление полученной простой схемы.

Схемы последовательного и параллельного соединения

Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.

При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений. При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.

Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.

Последовательное соединение считается наиболее простым. Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации.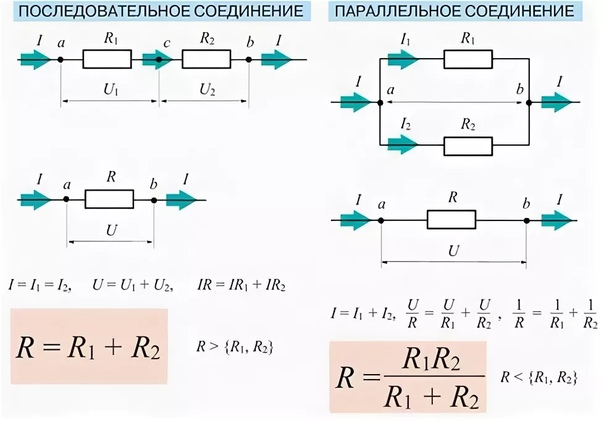 Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Смешанное соединение резисторов калькулятор — Мастер Фломастер

Содержание

1 Формула параллельного соединения резисторов
2 Параллельное соединение резисторов — расчет
3 Пример №1
4 Пример расчета №2
5 Как рассчитать сложные схемы соединения резисторов
6 Ток, протекающий в цепи параллельно соединенных резисторах
7 Параллельное соединение резисторов — онлайн калькулятор
8 Подведем итог
9 Калькулятор параллельных сопротивлений
10 Примеры применения параллельного соединения резисторов
11 Примеры расчетов
- - 11. 0.1 Электротехнические и радиотехнические калькуляторы

Для того чтобы определить общее эквивалентное сопротивление, можно воспользоваться точным и удобным калькулятором. Где, внеся данные по количеству резисторов, калькулятор произведет расчет в автоматическом режиме.

Данное соединение является одним из 2-ух видов, в данном случае оба вывода 1-го из резисторов соединяются с выводами 2-го резистора. В иных случаях их принято соединять параллельно или последовательно, чтобы можно было создать схемы сложного типа.

Для того чтобы найти ток, который протекает через определенный резистор, следует использовать формулу:
Произведем расчеты согласно примеру
Разрабатывается устройство, в котором есть необходимость использовать резистор, которое имеет сопротивление 8Ом. Исходя из того, что номинальный ряд согласно стандартным значениям таких резисторов не имеет, выходом будет использование 2-ух резисторов соединенных параллельно.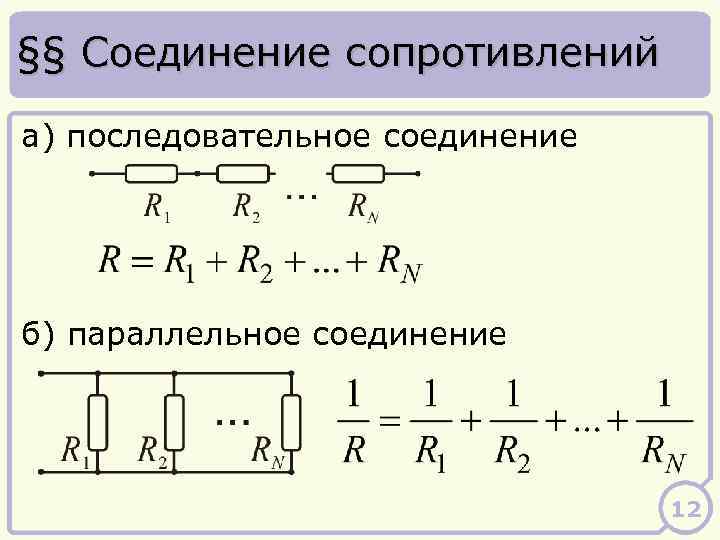

Для такого способа производятся следующие расчеты:

Данная формула показывает, что в случае когда R1 = R2, R будет составлять ровно половину сопротивления 1-го из 2-ух резисторов.
И если R=8Ом, то соответственно R1 и R2 = 2*8=16Ом.

Предложения и пожелания пишите на [email protected]

Поделитесь этим калькулятором на форуме или в сети!

Это помогает делать новые калькуляторы.

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.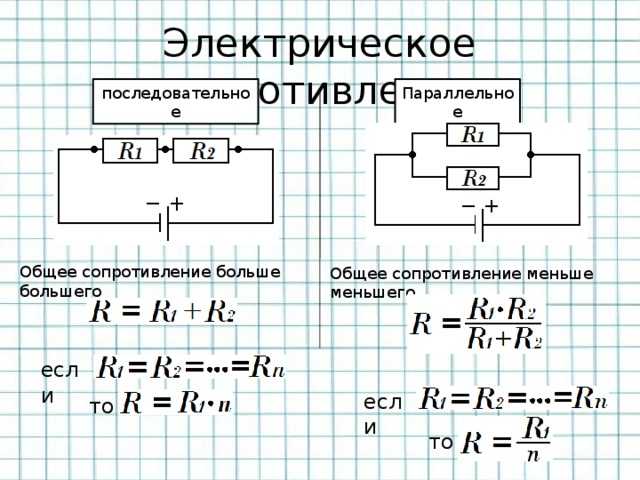 Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.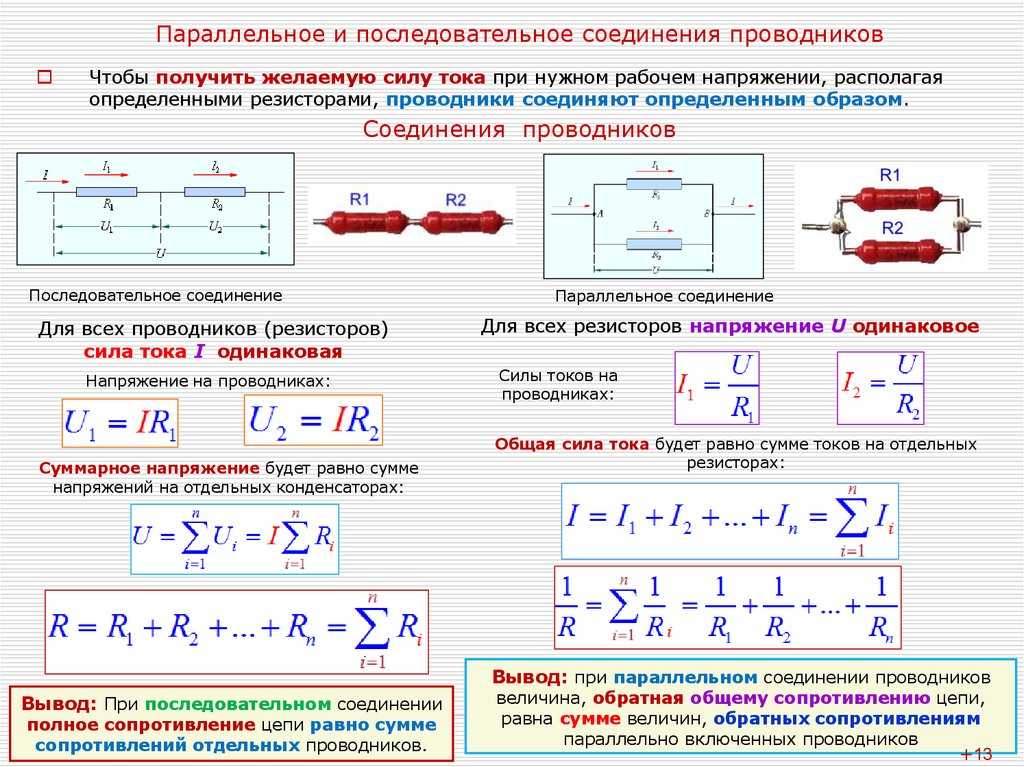

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.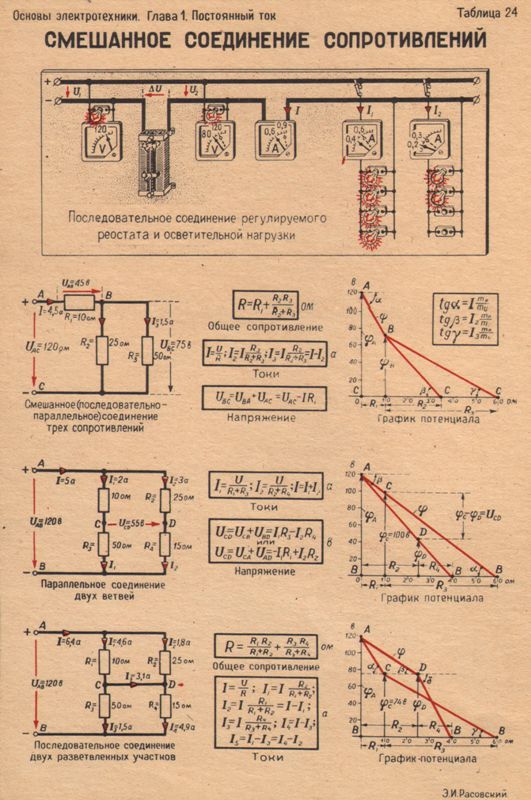

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

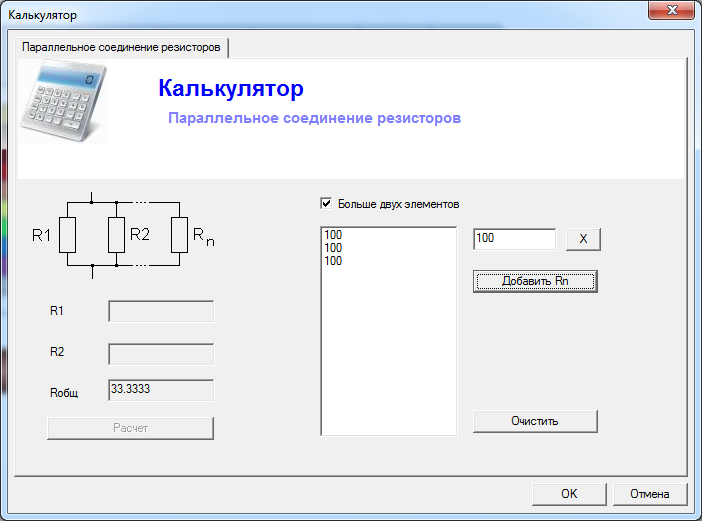
Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно.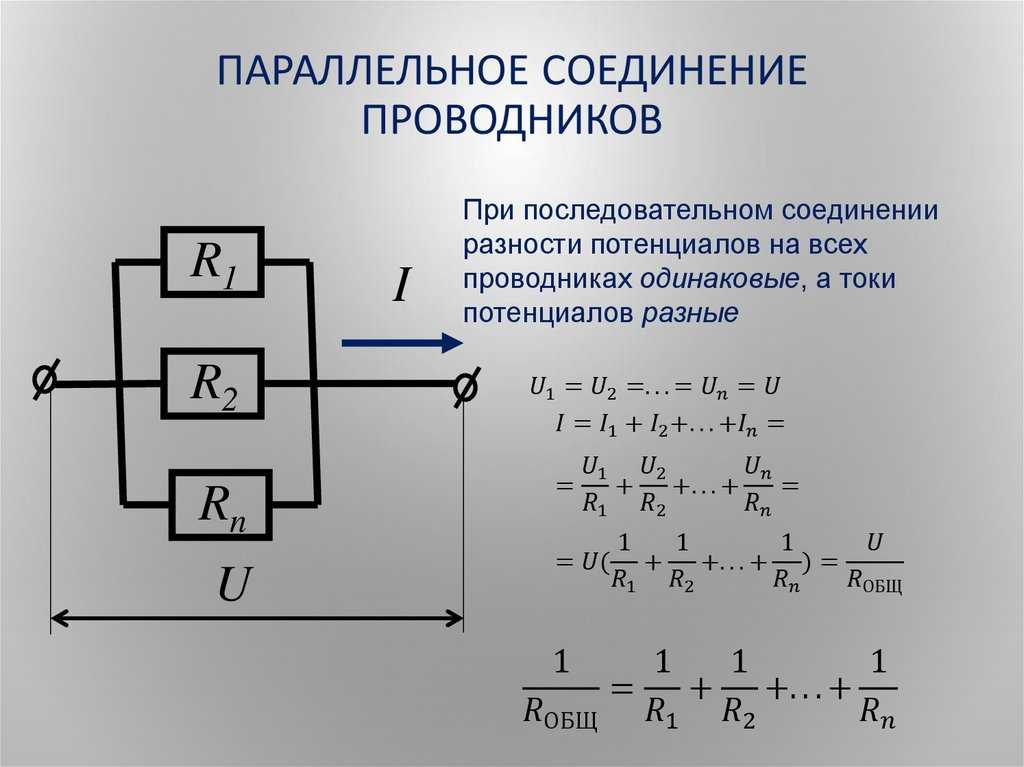 Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Калькулятор параллельных сопротивлений

Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.

Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.

Введите величины сопротивлений в поля R₁, R₂ и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.

1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.

Эквивалентное сопротивление R_eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.

Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:

Эта формула для R_eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:

Если параллельно соединены только два резистора, формула упрощается:

Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно

Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.

Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.

При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.

Примеры применения параллельного соединения резисторов

Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).

Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.

Примеры расчетов

Электротехнические и радиотехнические калькуляторы

Электроника — область физики и электротехники, изучающая методы конструирования и использования электронной аппаратуры и электронных схем, содержащих активные электронные элементы (диоды, транзисторы и интегральные микросхемы) и пассивные электронные элементы (резисторы, катушки индуктивности и конденсаторы), а также соединения между ними.
Радиотехника — инженерная дисциплина, изучающая проектирование и изготовление устройств, которые передают и принимают радиоволны в радиочастотной области спектра (от 3 кГц до 300 ГГц), также обрабатывают принимаемые и передаваемые сигналы. Примерами таких устройств являются радио- и телевизионные приемники, мобильные телефоны, маршрутизаторы, радиостанции, кредитные карточки, спутниковые приемники, компьютеры и другое оборудование, которое передает и принимает радиосигналы.
В этой части Конвертера физических единиц TranslatorsCafe.com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe. com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Как рассчитать падение напряжения на резисторе в параллельной цепи

Обновлено 28 декабря 2020 г.

Автор S. Hussain Ather

••• Syed Hussain Ather

TL;DR (слишком долго; не читал)

На приведенной выше схеме параллельных цепей падение напряжения можно найти путем суммирования сопротивлений каждого резистора и определения того, какое напряжение получается из тока в этой конфигурации. Эти примеры параллельных цепей иллюстрируют концепции тока и напряжения в разных ветвях.

На схеме параллельной цепи падение напряжения на резисторе в параллельной цепи одинаково на всех резисторах в каждой ветви параллельной цепи. Напряжение, выраженное в вольтах, измеряет электродвижущую силу или разность потенциалов, которая управляет цепью.

Когда у вас есть цепь с известной величиной тока , потока электрического заряда, вы можете рассчитать падение напряжения в схемах параллельных цепей по:

Определить комбинированный сопротивление или противодействие потоку заряда параллельных резисторов. Суммируйте их как 1/R _всего = 1/R ₁ + 1/R ₂ … для каждого резистора. Для приведенной выше параллельной цепи общее сопротивление можно найти как:
1. 1/R _общее = 1/5 Ом + 1/6 Ом + 1/10 Ом
2. 1/R _всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
3. 1/R _всего = 14/30 Ом
4. R _всего = 30/14 Ом = 15/7 Ом Закон Ома В = IR . Это равно падению напряжения во всей параллельной цепи и на каждом резисторе в параллельной цепи. Для этого примера падение напряжения равно В = 5 А x 15/7 Ом = 75/7 В. текущий уход. Это происходит из-за Текущий закон Кирхгофа , который гласит, что «алгебраическая сумма токов в сети проводников, сходящихся в одной точке, равна нулю». Калькулятор параллельной цепи будет использовать этот закон в ветвях параллельной цепи.
  Если мы сравним ток, входящий в три ветви параллельной цепи, он должен быть равен общему току, выходящему из ветвей. Поскольку падение напряжения остается постоянным на каждом параллельном резисторе, это падение напряжения, вы можете суммировать сопротивление каждого резистора, чтобы получить общее сопротивление и определить напряжение из этого значения. Примеры параллельных цепей показывают это.
  Падение напряжения в последовательной цепи
  ••• Сайед Хуссейн Атер
  С другой стороны, в последовательной цепи можно рассчитать падение напряжения на каждом резисторе, зная, что в последовательной цепи ток постоянен. через. Это означает, что падение напряжения на каждом резисторе разное и зависит от сопротивления в соответствии с законом Ома В = IR . В приведенном выше примере падение напряжения на каждом резисторе составляет:
  V_1=R_1I=3\times 3 = 9\text{ V}\\ V_2=R_2I=10\times 3 = 30\text{ V}\\ V_3=R_3I=5\times 3 = 15\text{ V}
  Сумма каждого падения напряжения должна быть равна к напряжению батареи в последовательной цепи. Это означает, что наша батарея имеет напряжение 54 В.
  Этот метод решения уравнений работает, потому что падения напряжения, поступающие на все резисторы, расположенные последовательно, должны суммироваться с общим напряжением последовательной цепи. Это происходит из-за закона напряжения Кирхгофа , который гласит, что «направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю». Это означает, что в любой заданной точке замкнутой последовательной цепи падения напряжения на каждом резисторе должны суммироваться с общим напряжением цепи. Поскольку ток в последовательной цепи постоянный, падение напряжения на каждом резисторе должно быть разным.
  Параллельные и последовательные цепи
  В параллельной цепи все компоненты цепи соединены между одними и теми же точками цепи. Это дает им их разветвленную структуру, в которой ток делится на каждую ветвь, но падение напряжения на каждой ветви остается одинаковым. Сумма каждого резистора дает общее сопротивление, основанное на инверсии каждого сопротивления ( 1/R _всего = 1/R ₁ + 1/R ₂ … для каждого резистора).
  В последовательной цепи, напротив, есть только один путь для протекания тока. Это означает, что ток остается постоянным, а падение напряжения на каждом резисторе разное. Сумма каждого резистора дает общее сопротивление при линейном суммировании ( R _всего = R ₁ + R ₂ … для каждого резистора).
  Последовательно-параллельные цепи
  Вы можете использовать оба закона Кирхгофа для любой точки или контура любой цепи и применить их для определения напряжения и тока. 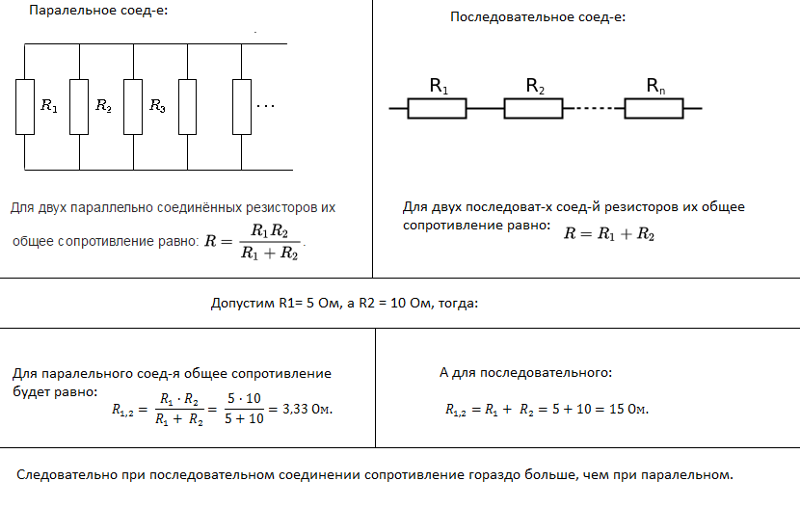Законы Кирхгофа дают вам метод определения тока и напряжения в ситуациях, когда характер цепи как последовательной и параллельной может быть не таким простым.
  Как правило, для цепей, которые имеют как последовательные, так и параллельные компоненты, вы можете рассматривать отдельные части схемы как последовательные или параллельные и комбинировать их соответствующим образом.
  Эти сложные последовательно-параллельные схемы можно решить несколькими способами. Обработка их частей как параллельных или последовательных — это один из методов. Еще одним методом является использование законов Кирхгофа для определения обобщенных решений, использующих систему уравнений. Калькулятор последовательно-параллельных цепей будет учитывать различную природу цепей.
  ••• Syed Hussain Ather
  В приведенном выше примере текущая точка отправления A должна совпадать с текущей точкой отправления A. Это означает, что вы можете написать:
  (1). I_1=I_2+I_3\text{ или }I_1-I_2-I_3=0
  Если вы рассматриваете верхний контур как замкнутую последовательную цепь и рассматриваете падение напряжения на каждом резисторе, используя закон Ома с соответствующим сопротивлением, вы можете написать:
  (2). 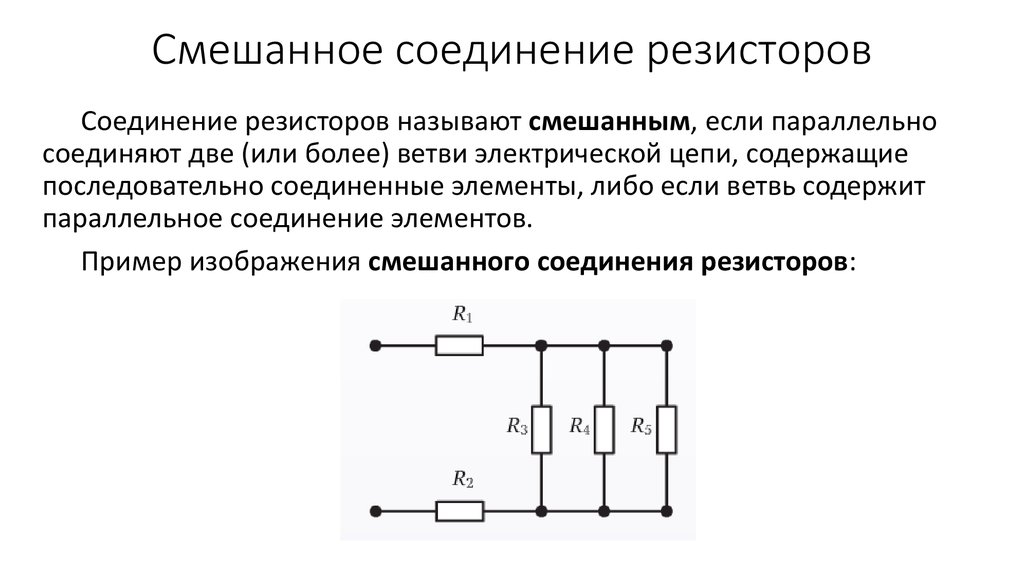V_1-R_1I_1-R_2I_2=0
  и, делая то же самое для нижнего контура, вы можете рассматривать каждое падение напряжения в направлении тока как зависящее от тока и сопротивления, чтобы записать:
  (3). V_1+V_2+R_3I_3-R_2I_2=0
  Это дает вам три уравнения, которые можно решить несколькими способами. Вы можете переписать каждое из уравнений (1) — (3) так, чтобы напряжение было на одной стороне, а ток и сопротивление — на другой. Таким образом, вы можете рассматривать три уравнения как зависящие от трех переменных I ₁ , I ₂ и I ₃ с коэффициентами комбинаций R ₁ , R ₂ и R ₃ .
  \begin{выровнено}&(1). I_1-I_2-I_3=0\\ &(2). R_1I_1+R_2I_2+0\times I_3=V_1\\ &(3). 0\раз I_1+R_2I_2-R_3I_3=V_1+V_2\конец{выровнено}
  Эти три уравнения показывают, как напряжение в каждой точке цепи каким-то образом зависит от тока и сопротивления. Если вы помните законы Кирхгофа, вы можете создать эти обобщенные решения для проблем со схемами и использовать для их решения матричную запись. 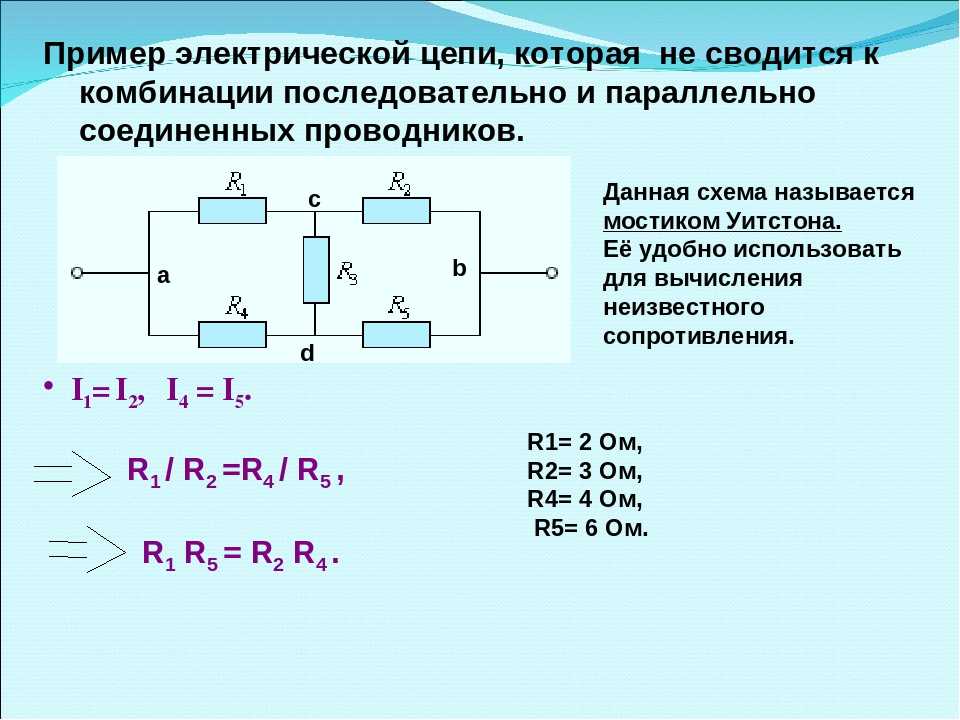Таким образом, вы можете подставить значения для двух величин (напряжение, ток, сопротивление), чтобы найти третью.
  Series and Parallel — AP Physics 1
  Все ресурсы AP Physics 1
  7 Диагностические тесты
  170 практических тестов
  Вопрос дня
  Карточки
  Учитесь по концепции
  ← Предыдущая 1 2 Следующая →
  AP Physics 1 Справка »
  Электричество и волны »
  Электричество »
  Схемы »
  Последовательная и параллельная
  Цепь имеет резистор с сопротивлением , за которым следуют три параллельных ответвления, каждое из которых содержит резистор с сопротивлением . Чему равно полное эквивалентное сопротивление цепи?
  Возможные ответы:
  Правильный ответ:
  Объяснение:
  Во-первых, нам нужно рассчитать эквивалентное сопротивление трех параллельно соединенных резисторов. 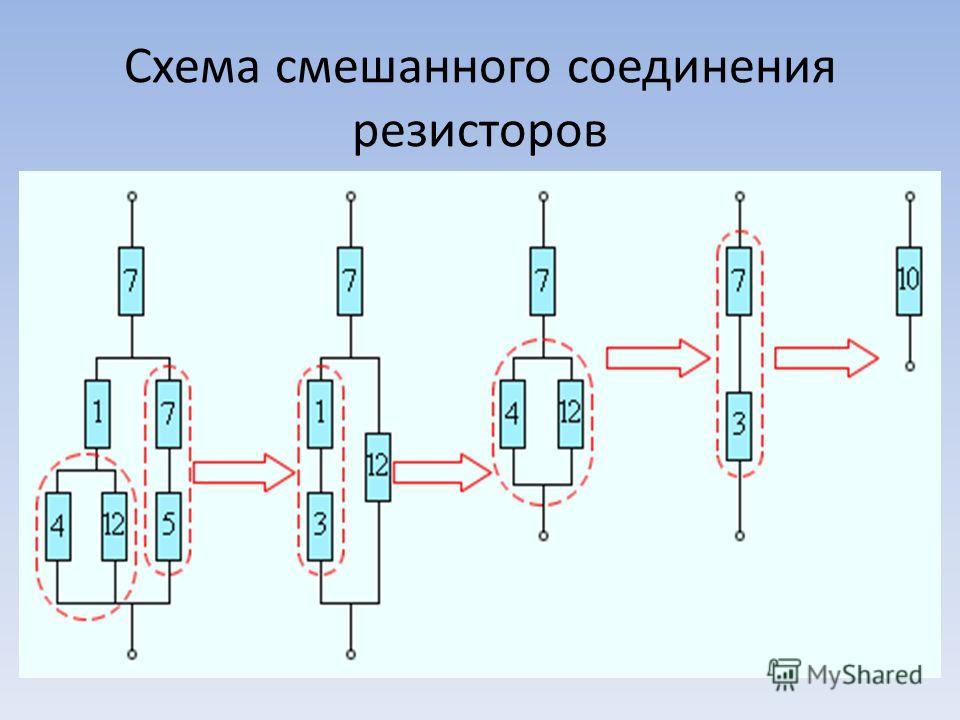Для этого воспользуемся следующим уравнением:
  Теперь, чтобы получить общее эквивалентное сопротивление, мы можем просто сложить два оставшихся значения, так как они идут последовательно:
  Сообщить об ошибке
  Рассмотрим данную цепь:
  К точкам A и B приложено напряжение, так что ток течет от A к R2 и к B. Каково значение этого напряжения, если ток через R2 равен 4 А?
  Возможные ответы:
  Правильный ответ:
  Объяснение:
  Во-первых, нам нужно рассчитать ток, протекающий через резистор R2 без дополнительного напряжения. Нам нужно будет рассчитать полное эквивалентное сопротивление цепи. Поскольку два резистора включены последовательно, мы можем просто добавить их.
  Тогда мы можем использовать закон Ома для расчета тока в цепи:
  Теперь, когда у нас есть ток, мы можем рассчитать дополнительный ток, который вносит новое напряжение: мы можем рассчитать, каким должно быть это напряжение, чтобы обеспечить новый ток:
  Сообщить об ошибке
  Каково эффективное сопротивление этой цепи постоянного тока?
  Возможные ответы:
  Ни один из других ответов
  
  Объяснение:
  Во-первых, давайте напомним себе, что эффективное сопротивление последовательно соединенных резисторов равно и эффективное сопротивление параллельно подключенных резисторов равно .
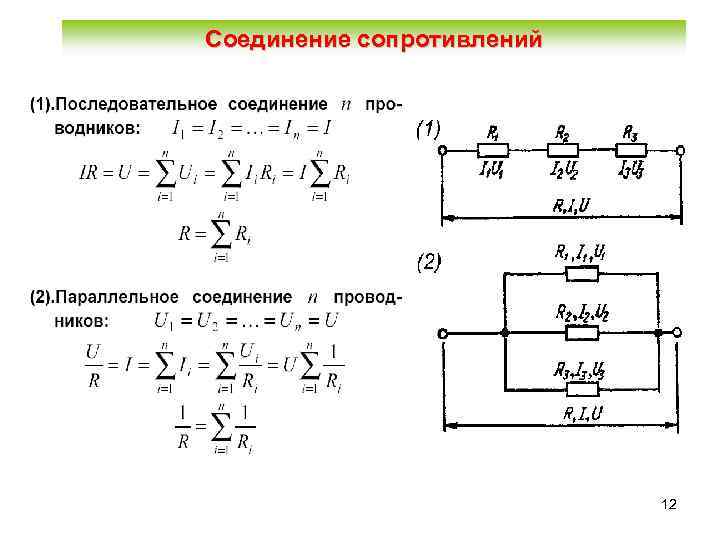
  Начните эту задачу с определения эффективного сопротивления резисторов 2, 3 и 4:
  (Это потому, что эти три резистора включены последовательно.)
  Теперь схему можно упростить до следующей:
  
  Далее нам нужно будет определить эффективное сопротивление резисторов и 6:
  Опять же, схему можно упростить:
  Отсюда , эффективное сопротивление цепи постоянного тока можно определить, вычислив эффективное сопротивление резисторов , 1 и 5:
  Сообщить об ошибке
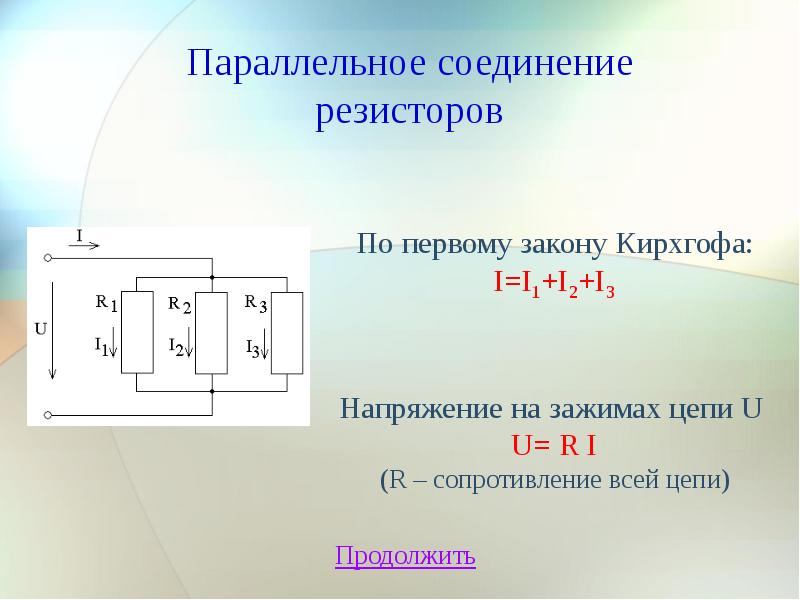
  Две лампочки, одна с номиналом , а другая с номиналом , соединены последовательно с батареей . Какой из них будет ярче? А если их подключить параллельно?
  Возможные ответы:
  Не хватает информации, чтобы выполнить эту проблему
  Серия:
  Параллель:
  Серия:
  Параллель:
  Серия:
  Параллель:
  Series:
  :
  :
  Series:
  :
  :
  .
  Ряд:
  Параллельный:
  Правильный ответ:
  Ряд:
  Параллельный:
  Объяснение:
  Первый шаг к решению этой проблемы — выяснить, как сопротивление лампочки соотносится с номинальной мощностью. Для резистора рассеиваемая мощность равна:
  Таким образом, существует обратная зависимость между сопротивлением лампочки и номинальной мощностью.
  Вторым шагом является рассмотрение элементов схемы, соединенных последовательно и параллельно. Последовательно они имеют один и тот же ток; параллельно они делят одно и то же напряжение. Таким образом, для двух последовательно соединенных лампочек ярче будет та, у которой больше сопротивление (меньшая мощность), а для параллельной конфигурации ярче будет лампочка с меньшим сопротивлением (больше мощность).
  Сообщить об ошибке
  Если у нас есть 3 последовательно соединенных резистора, причем резистор 1 имеет сопротивление , резистор 2 имеет сопротивление , а резистор 3 имеет сопротивление , каково эквивалентное сопротивление серии?
  Возможные ответы:
  Правильный ответ:
  Пояснение:
  Общее сопротивление последовательно соединенных резисторов равно сумме их индивидуальных сопротивлений. В этом случае
  Сообщить об ошибке
  Вам представлены три резистора, каждый размер . В чем разница между общим сопротивлением резисторов, соединенных последовательно, и полным сопротивлением резисторов, соединенных параллельно?
  Возможные ответы:
  Правильный ответ:
  Объяснение:
  Резисторы последовательно:
  Параллельные резисторы:
  Сообщить об ошибке
  Каково общее сопротивление трех резисторов, , , и , включенных параллельно?
  Возможные ответы:
  Правильный ответ:
  Объяснение:
  Уравнение эквивалентного сопротивления для нескольких резисторов, включенных параллельно:
  Подставьте известные значения и решите.
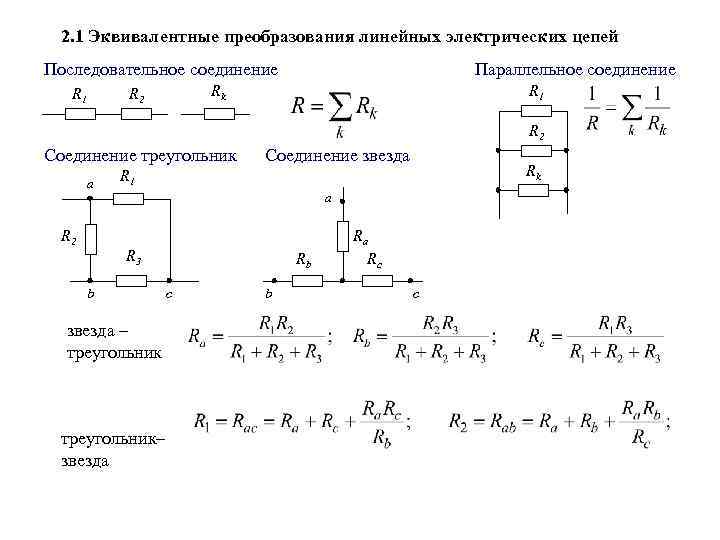
  Обратите внимание, что для параллельных резисторов общее сопротивление никогда не превышает сопротивления наименьшего элемента.
  Сообщить об ошибке
  Цепь создается с использованием батареи и 3-х одинаковых резисторов, как показано на рисунке. Каждый из резисторов имеет сопротивление . Если резистор удалить из цепи, как это повлияет на ток через резистор?
  Возможные ответы:
  Проходной ток увеличится в два раза
  Проходной ток останется прежним
  Проходной ток уменьшится
  Проходной ток увеличится в четыре раза
  Невозможно определить, не зная удельного сопротивления провода
  Правильный ответ:
  Ток через уменьшится
  Объяснение:
  Поскольку резисторы и образуют параллельную сеть, удаление из цепи увеличивает сопротивление этой части цепи. 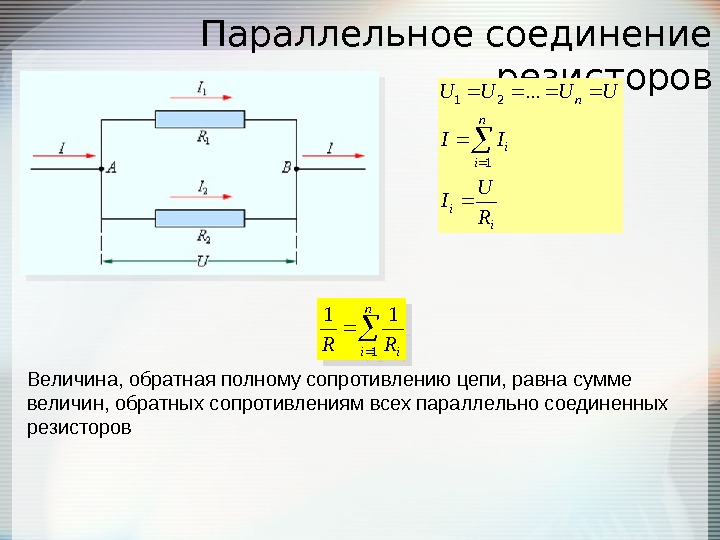Поскольку новая схема представляет собой последовательную комбинацию и , увеличенное сопротивление приводит к снижению тока в каждом из этих резисторов.
  Сообщить об ошибке
  Определите общий заряд, хранящийся в цепи с двумя одинаковыми плоскопараллельными конденсаторами, соединенными параллельно, с площадью и расстоянием между параллельными пластинами. Предположим, что пространство между параллельными пластинами представляет собой вакуум. Схема показывает разницу напряжений 10 В.
  Возможные ответы:
  Правильный ответ:
  Объяснение:
  Чтобы определить общий накопленный заряд, нам нужно сложить емкость каждого конденсатора (поскольку они соединены параллельно) и умножить на разницу напряжений. Напомним, что для конденсаторов
  Для конденсаторов с параллельными пластинами:
  Здесь, , которая представляет собой диэлектрическую проницаемость пустого пространства, является диэлектрической проницаемостью, которая из-за присутствия только вакуума, , которая представляет собой площадь параллельных пластин, и , что является расстоянием между пластинами.
  Подставьте известные значения для определения емкости.
  Каждый из двух конденсаторов имеет емкость
  Поскольку конденсаторы подключены параллельно, общая емкость представляет собой сумму емкостей каждого из них. Общая емкость в цепи определяется как:
  Подставьте это значение в наше первое уравнение и найдите общий накопленный заряд.
  , где — общий заряд, хранящийся в конденсаторе. Начиная с
  Сообщить об ошибке
  Каков общий ток, протекающий через систему с 2 параллельными резисторами с сопротивлением и и аккумулятором с разностью напряжений 10 В?
  Возможные ответы:
  Правильный ответ:
  Объяснение:
  Сначала нам нужно определить общее сопротивление цепи, прежде чем мы узнаем, какой ток протекает через нее. Поскольку резисторы подключены параллельно, их сопротивления складываются обратно:
  , где — общее сопротивление цепи.