Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования. Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п. Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям. Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением, а разность e = (x0 − x) — невязкой, рассогласованием или отклонением величины от заданной. Выходной сигнал регулятора u определяется тремя слагаемыми: где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму: где — время дискретизации. Используя замену можно записать: В программной реализации для оптимизации расчетов переходят к рекуррентной формуле: Часто в качестве параметров ПИД-регулятора используются: Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. dic.academic.ru В предыдущей статье мы разобрались с принципом работы ПИД-регулятора (ссылка). Теперь, как и обещал, рассмотрим основные методы настройки и подбора его коэффициентов ) Вообще, по большому счету, при использовании ПИД-регулятора необходимо построить модель всей системы в целом и математически вычислить необходимые значения коэффициентов. Так делать правильно. Но, естественно, так никто не делает 😉 На самом деле, математический расчет коэффициентов задача далеко не тривиальная, требует глубоких знаний теории автоматического управления, поэтому и используются другие, упрощенные, методы настройки. Собственно, на этом практическая часть метода заканчивается ) Из полученного коэффициента А из него получаем и остальные: Метод довольно прост, но применить его можно далеко не всегда. Если честно, мне еще ни разу не приходилось настраивать регулятор таким образом 😉 Но тем не менее, этот метод является основным и, по большому счету, единственным широко известным. Просто подходит не всем и не всегда. Что же делать, если метод Циглера-Никольса не сработал? Тут придет на помощь “аналитический” метод настройки =) Опять же обнуляем все коэффициенты и начинаем увеличивать пропорциональный. Но теперь не ждем появления колебаний, а просто фиксируем поведение системы для каждого значения коэффициента (отличным вариантом будет построение графика величины, которую необходимо стабилизировать, для каждого значения коэффициента). Если видим, что, например, система очень медленно выходит на нужное значение, увеличиваем пропорциональный коэффициент. Система начинает сильно колебаться относительно нужной величины? Значит, коэффициент слишком велик, уменьшаем и переходим к настройке других составляющих. Понимая, как работает ПИД-регулятор в целом, и представляя, как должна работать настраиваемая система, можно довольно-таки быстро и точно настроить коэффициенты регулятора. Особенно, если есть возможность построить графические зависимости и визуально следить за поведением системы. Вот некоторые правила, которые могут помочь при настройке: Кстати, стоит добавить, что не всегда необходимо использовать все три составляющие ПИД-регулятора, порой хватает пропорциональной и дифференциальной, например (ПД-регулятор). В общем, все сводится к тому, что для каждой системы необходим свой собственный подход при настройке и использовании ПИД-регулятора. На этом на сегодня все, возможно, как-нибудь рассмотрим практическую реализацию ПИД-регулятора 😉 microtechnics.ru Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования. Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п. Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям. Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением, а разность e = (x0 − x) — невязкой, рассогласованием или отклонением величины от заданной. Выходной сигнал регулятора u определяется тремя слагаемыми: где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму: где — время дискретизации. Используя замену можно записать: В программной реализации для оптимизации расчетов переходят к рекуррентной формуле: Часто в качестве параметров ПИД-регулятора используются: Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. veter.academic.ru В данной статье приведены основные принципы и правила настройки коэффициентов ПИД-регулятора сточки зрения практического применения. Теоретические основы можно прочитать вот в этой статье. Для простоты изложения рассмотрим настройку регулятора на примере. Допустим, необходимо поддерживать температуру в помещении с помощью обогревателя, управляемого регулятором. Для измерения текущей температуры используем термопару. Настройка регулятора производится с одной единственной целью: подобрать его коэффициенты для данной задачи таким образом, чтобы регулятор поддерживал величину физического параметра на заданном уровне. В нашем примере физическая величина — это температура. Допустим текущая температура в помещении 10 °С, а мы хотим, чтобы было 25°С. Мы включаем регулятор и он начинает управлять мощностью обогревателя таким образом, чтобы температура достигла требуемого уровня. Посмотрим как это может выглядеть. Чёрным цветом показан график изменения температуры в том случае, если коэффициенты подобраны совсем плохо. Система теряет устойчивость. Регулятор при этом идёт «в разнос» и температура «уходит» от заданного значения. Рассмотрим более благоприятные случаи. А вот и приемлемые кривые: В процессе настройки регулятора, пользователю необходимо стремиться получить кривую, близкую к идеальной. Однако, в реальных условиях сделать это не так-то просто — приходится долго и мучительно подбирать коэффициенты. Поэтому зачастую останавливаются на «приемлемой» кривой регулирования. Например, в нашем примере нас могли бы устроить коэффициенты регулятора, при которых заданная температура достигалась бы за 15-20 минут с максимальным перерегулированием (максимальными «скачками» температуры) 2 °С. А вот время достижение уставки более часа и максимальные «скачки» температуры 5 °С — нас бы не устроили. Далее поговорим о том, как подобрать коэффициенты для достижения оптимального регулирования. Рекомендуется настраивать коэффициенты в том же порядке, в котором это описано. Выставляем дифференциальный и интегральный коэффициенты в ноль, тем самым убирая соответствующие составляющие. Пропорциональный коэффициент выставляем в 1. Далее нужно задать значение уставки температуры отличное от текущей и посмотреть, как регулятор будет менять мощность обогревателя, чтобы достичь заданного значения. Характер изменения можно отследить «визуально», если у вас получится мысленно представить этот график. Либо можно регистрировать в таблицу измеренное значение температуры каждые 5-10 секунд и по полученным значением построить график. Затем нужно проанализировать полученную зависимость в соответствии с рисунком: Постепенно увеличивая дифференциальную составляющую, необходимо добиться уменьшения или полного исчезновения «скачков» графика (перерегулирования) перед выходом на уставку. При этом кривая должна стать еще больше похожа на идеальную. Если слишком сильно завысить дифференциальный коэффициент, температура при выходе на уставку будет расти не плавно, а скачками (как показано на рисунке). При появлении таких скачков необходимо прекратить увеличение дифференциального коэффициента. При настройке двух предыдущих коэффициентов можно получить практически идеальную кривую регулирования или близкую к ней кривую, удовлетворяющую условиям задачи. Однако, как правило возникает так называемая «статическая ошибка». При этом в нашем примере температура стабилизируется не на заданном значении 25 °С, а на несколько меньшем значении. Дело в том, что если температура станет равной уставке (то есть разность текущей и заданной температур станет равна 0), то пропорциональная и дифференциальная составляющая будут равны нулю (см. функцию преобразования ПИД-регулятора). При этом мощность регулятора тоже станет равна 0 и он начнёт остывать. Для того чтобы исключить этот эффект, используют интегральную составляющую. Её необходимо постепенно увеличивать до исчезновение статической ошибки. Однако, чрезмерное её увеличение тоже может привести к возникновению скачков температуры. Настройка ПИД-регулятора довольно сложный и трудоёмкий процесс. На практике достаточно тяжело достичь оптимального регулирования и зачастую в этом нет необходимости. Чаще всего достаточно добиться такого вида переходного процесса, который устроит пользователя в условиях текущей задачи. lazysmart.ru Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования. Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п. Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям. Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением, а разность e = (x0 − x) — невязкой, рассогласованием или отклонением величины от заданной. Выходной сигнал регулятора u определяется тремя слагаемыми: где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму: где — время дискретизации. Используя замену можно записать: В программной реализации для оптимизации расчетов переходят к рекуррентной формуле: Часто в качестве параметров ПИД-регулятора используются: Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. dik.academic.ru Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования. Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п. Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям. Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением, а разность e = (x0 − x) — невязкой, рассогласованием или отклонением величины от заданной. Выходной сигнал регулятора u определяется тремя слагаемыми: где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму: где — время дискретизации. Используя замену можно записать: В программной реализации для оптимизации расчетов переходят к рекуррентной формуле: Часто в качестве параметров ПИД-регулятора используются: Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. dikc.academic.ru Пропорционально-интегрально-дифференциальный (ПИД) регулятор — устройство в управляющем контуре с обратной связью. Используется в системах автоматического управления для формирования управляющего сигнала с целью получения необходимых точности и качества переходного процесса. ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования. Если какие-то из составляющих не используются, то регулятор называют пропорционально-интегральным, пропорционально-дифференциальным, пропорциональным и т. п. Пропорциональная составляющая вырабатывает выходной сигнал, противодействующий отклонению регулируемой величины от заданного значения, наблюдаемому в данный момент времени. Он тем больше, чем больше это отклонение. Если входной сигнал равен заданному значению, то выходной равен нулю. Однако при использовании только пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к заданной, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь заданного значения, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления, при наличии задержек в системе, могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая пропорциональна интегралу от отклонения регулируемой величины. Её используют для устранения статической ошибки. Она позволяет регулятору со временем учесть статическую ошибку. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Тем не менее, интегральная составляющая также может приводить к автоколебаниям. Дифференциальная составляющая пропорциональна темпу изменения отклонения регулируемой величины и предназначена для противодействия отклонениям от целевого значения, которые прогнозируются в будущем. Отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Назначение ПИД-регулятора — в поддержании заданного значения x0 некоторой величины x с помощью изменения другой величины u. Значение x0 называется заданным значением, а разность e = (x0 − x) — невязкой, рассогласованием или отклонением величины от заданной. Выходной сигнал регулятора u определяется тремя слагаемыми: где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: В дискретной реализации метода расчета выходного сигнала уравнение принимает следующую форму: где — время дискретизации. Используя замену можно записать: В программной реализации для оптимизации расчетов переходят к рекуррентной формуле: Часто в качестве параметров ПИД-регулятора используются: Следует учитывать, что термины используются по-разному в различных источниках и разными производителями регуляторов. dis.academic.ruНастройка ПИД-регулятора. Пид регулятор что это
регулятор - это... Что такое ПИД-регулятор?
Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации. Общие сведения
Пропорциональная составляющая
Интегральная составляющая
Дифференциальная составляющая
Теория
Ссылки
Настройка коэффициентов ПИД-регулятора. | MicroTechnics
 Наиболее часто использующимся методом настройки коэффициентов является метод Циглера-Никольса. Заключается он в следующем…
Наиболее часто использующимся методом настройки коэффициентов является метод Циглера-Никольса. Заключается он в следующем…Метод Циглера-Никольса.
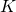 , при котором это произошло. Кроме того, замеряем период колебаний системы
, при котором это произошло. Кроме того, замеряем период колебаний системы 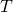 .
.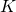 рассчитываем пропорциональный коэффициент ПИД-регулятора:
рассчитываем пропорциональный коэффициент ПИД-регулятора:![Rendered by QuickLaTeX.com \[K_p = K * 0.6\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-0c5de49a5de647bd075d337118cbf0ed_l3.png)
![Rendered by QuickLaTeX.com \[K_u = (2 * K_p) / T\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-ac3c082fac3fe1bc0dd232d6f4463aae_l3.png)
![Rendered by QuickLaTeX.com \[K_g = (K_p * T) / 8\]](/800/600/https/microtechnics.ru/wp-content/ql-cache/quicklatex.com-cb2ce36d6c9e5cb5f2507adbb70ff096_l3.png)
регулятор - это... Что такое ПИД-регулятор?
Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации. Общие сведения
Пропорциональная составляющая
Интегральная составляющая
Дифференциальная составляющая
Теория
Ссылки
Практические советы по настройке ПИД-регулятора
Задача настройки
 На данном рисунке красным цветом показана идеальная кривая изменения температуры в помещении при работе регулятора. Физическая величина плавно, без скачков, но в тоже время достаточно быстро подходит к заданному значению. Оптимальное время, за которое температура может достигнуть заданной отметки, определить довольно сложно. Оно зависит от многих параметров: размеров комнаты, мощности обогревателя и др. В теории это время можно рассчитать, но на практике чаще всего это определяется экспериментально.
На данном рисунке красным цветом показана идеальная кривая изменения температуры в помещении при работе регулятора. Физическая величина плавно, без скачков, но в тоже время достаточно быстро подходит к заданному значению. Оптимальное время, за которое температура может достигнуть заданной отметки, определить довольно сложно. Оно зависит от многих параметров: размеров комнаты, мощности обогревателя и др. В теории это время можно рассчитать, но на практике чаще всего это определяется экспериментально. На этом рисунке показаны графики, далёкие от идеального. В первом случае наблюдается сильное перерегулирование: температура слишком долго «скачет» относительно уставки, прежде чем достичь её. Во втором случае регулирование происходит плавно, но слишком медленно.
На этом рисунке показаны графики, далёкие от идеального. В первом случае наблюдается сильное перерегулирование: температура слишком долго «скачет» относительно уставки, прежде чем достичь её. Во втором случае регулирование происходит плавно, но слишком медленно. Данные кривые тоже не идеальны, но могут быть сочтены за удовлетворительные.
Данные кривые тоже не идеальны, но могут быть сочтены за удовлетворительные.Настраиваем пропорциональный коэффициент
 При большом перерегулировании, необходимо уменьшать пропорциональный коэффициент, а если регулятор долго достигает уставки — увеличивать. Так убавляя-прибавляя коэффициент необходимо получить график регулирования как можно ближе к идеальному. Поскольку достичь идеала удастся вряд ли, лучше оставить небольшое перерегулирование (его можно будет скорректировать другими коэффициентами), чем длительное нарастание графика.
При большом перерегулировании, необходимо уменьшать пропорциональный коэффициент, а если регулятор долго достигает уставки — увеличивать. Так убавляя-прибавляя коэффициент необходимо получить график регулирования как можно ближе к идеальному. Поскольку достичь идеала удастся вряд ли, лучше оставить небольшое перерегулирование (его можно будет скорректировать другими коэффициентами), чем длительное нарастание графика.Настраиваем дифференциальный коэффициент

Настраиваем интегральный коэффициент

Заключение
регулятор - это... Что такое ПИД-регулятор?
Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации. Общие сведения
Пропорциональная составляющая
Интегральная составляющая
Дифференциальная составляющая
Теория
Ссылки
регулятор - это... Что такое ПИД-регулятор?
Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации. Общие сведения
Пропорциональная составляющая
Интегральная составляющая
Дифференциальная составляющая
Теория
Ссылки
регулятор - это... Что такое ПИД-регулятор?
Схема, иллюстрирующая принцип работы ПИД-регулятора. Коэффициенты перед интегралом и производной опущены для большей наглядности иллюстрации. Общие сведения
Пропорциональная составляющая
Интегральная составляющая
Дифференциальная составляющая
Теория
Ссылки
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''








Поделиться с друзьями: