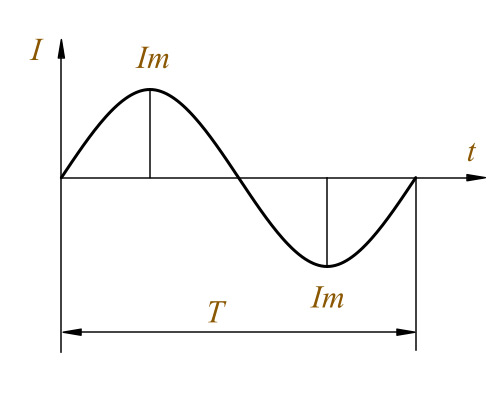
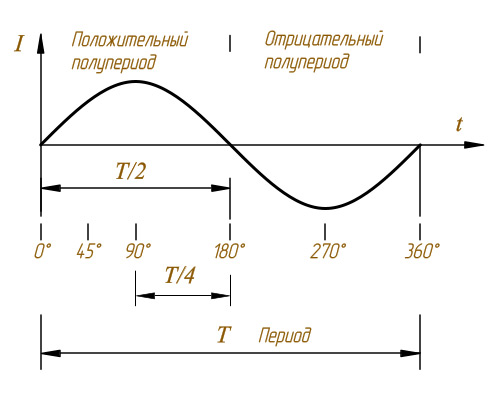
Переменный ток – или AC (Alternating Current). Обозначение ( ~ ). Электрический ток называется переменным, если он в течение времени меняет свое направление и непрерывно изменяется по величине. Переменный ток, который используется для подключения бытовых или производственных электрических приборов, изменяется по синусоидальному закону: График переменного тока Широко используется переменный ток благодаря тому, что электроэнергия переменного тока технически просто и экономно может быть преобразована из энергии более низкого напряжения в энергию более высокого напряжения и наоборот. Это свойство переменного тока позволяет передавать электроэнергию по проводам на большие расстояния. Период переменного тока Промышленный переменный электрический ток получают при помощи электрических генераторов, принцип работы которых основан на законе электромагнитной индукции. Вращение генератора осуществляется механическим двигателем, использующим тепловую, гидравлическую или атомную энергию. Переменный однофазный электрический ток имеет следующие основные характеристики: f – частота переменного тока определяет количество циклов или периодов в единицу времени. За единицу измерения частоты переменного тока принят Герц ( Гц ): 1гц = 103кгц = 106мгц Τ – период – время одного полного изменения переменной величины. Если в 1 секунду происходит 1 период Τ, то частота f = 1 Гц ( Герц ). 1c = 103мс = 106мкс = 1012нс В Российской Федерации период Τ переменного тока принят равным 0,02 секунды,следовательно по формуле
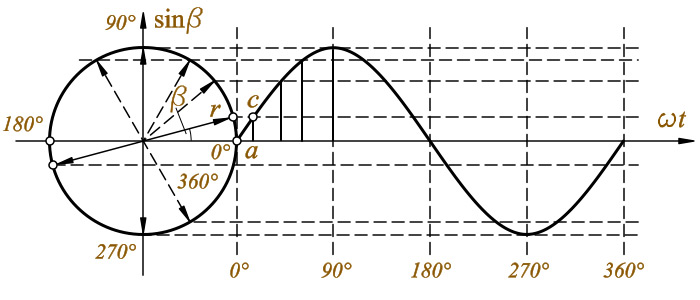
f = 1/Τ можно определить частоту переменного тока: f = 1/0,02 = 50 Гц ω – угловая скорость Помимо частоты f при изучении цепей переменного тока вводится понятие угловой скорости ω. Угловая скорость ω связана с частотой f следующим соотношением: ω=2πf При частоте 50 Гц угловая скорость равна 314 рад/с (2 × 3,14 × 50 = 314). Мгновенное значение (i,u,e,p) – значение величины в данный момент, мгновенное. Максимальное или амплитудное значение (Im,Um,Em,Pm). Эффективное значение тока – это величина переменного тока, равная такому току, который на сопротивлении R, создаёт тепловыделение равное данному переменному току, за тоже время t (I,U,E,P). В системе декартовых прямоугольных координат совмещены тригонометрический круг и кривая, отражающая изменение величины тригонометрической функции sinβ от величины угла β между осью 0х и радиусом-вектором r. Радиус-вектор r вращается против часовой стрелки. Повернем радиус-вектор на угол β и от конца вектора r проведем пунктиром прямую, параллельную оси 0х. От окружности (точка а) по оси 0х отложим в масштабе отрезок. Из конца отрезка построим перпендикуляр до пересечения с пунктирной прямой. Получим точку с в пересечении перпендикуляра и пунктирной прямой. Синусоида переменного тока Аналогичное построение проведем, увеличивая угол β, пока радиус-вектор повернется на угол β = 360°, и получим точки аналогично точке с. Соединим точки плавной кривой, которая и будет отражать синусоидальный закон изменения величины переменного тока. Если две переменные величины одновременно проходят свои нулевые и максимальные значения, то они совпадают по фазе. Если две переменные величины не одновременно проходят свои нулевые и максимальные значения, то они не совпадают по фазе. В радиотехнике используются понятия: 1. Активное сопротивление ( Ra ) 2. Индуктивное сопротивление ( XL – реактивное сопротивление ) 3. Ёмкостное сопротивление ( XC – реактивное сопротивление ) Если по проводнику протекает ток, то вследствие явления самоиндукции, электроны распространяются не равномерно по сечению проводника, вследствие чего растёт сопротивление проводника. Явление неравномерного распространения зарядов по сечению проводника называется – поверхностный эффект. Чем больше частота, тем больше сопротивление. selectelement.ru Переме́нный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным[1]. Хотя переменный ток часто переводят на английский как alternating current, эти термины не являются эквивалентными. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ∼{\displaystyle \thicksim } или ≈{\displaystyle \thickapprox } (знак синусоиды), или латинскими буквами AC{\displaystyle AC}. Так как переменный ток в общем случае меняется в электрической цепи не только по величине, но и по направлению, то одно из направлений переменного тока в цепи считают условно положительным, а другое, противоположное первому, условно отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной. П ru-wiki.ru П. т. широко применяется в устройствах связи (радио, телевидение, проволочная телефония на дальние расстояния и т. п.). П. т. создаётся переменным напряжением. Переменное электромагнитное поле, возникающее в пространстве, окружающем проводники с током, вызывает колебания энергии в цепи П. т.: энергия периодически то накапливается в магнитном или электрическом поле, то возвращается источнику электроэнергии. Колебания энергии создают в цепи П. т. реактивные токи, бесполезно загружающие провода и источник тока и вызывающие дополнительные потери энергии, что является недостатком передачи энергии П. т. За основу для характеристики силы П. т. принято сопоставление среднего теплового действия П. т. с тепловым действием постоянного тока соответствующей силы. Полученное таким путём значение силы П. т. I называется действующим (или эффективным) значением, математически представляющим среднеквадратичное за период значение силы тока. Аналогично определяется и действующее значение напряжения П. т. U. Амперметры и вольтметры П. т. измеряют именно действующие значения тока и напряжения. В цепи, не содержащей ни индуктивности, ни ёмкости, ток совпадает по фазе с напряжением (рис. 3). Закон Ома для действующих значений в этой цепи будет иметь такую же форму, как для цепи постоянного тока: I = U/r. Здесь r — активное сопротивление цепи, определяемое по активной мощности Р, затрачиваемой в цепи: r = P/I2. При наличии в цепи индуктивности L П. т. индуцирует в ней эдс самоиндукции eL= — L. di/dt = — ωLlmcos (ωt + α) = ωLImsin (ωt + α — π/2). Эдс самоиндукции противодействует изменениям тока, и в цепи, содержащей только индуктивность, ток отстаёт по фазе от напряжения на четверть периода, то есть φ=π/2 (рис. 4). Действующее значение eL равно EL = IωL = IxL, где xL = ωL — индуктивное сопротивление цепи. Закон Ома для такой цепи имеет вид: I = U/xL = U/ωL. Когда ёмкость С включена под напряжение u, то её заряд равен q = Cu. Периодические изменения напряжения вызывают периодические изменения заряда, и возникает ёмкостный ток i = dq/dt = C․du/dt = (CUm cos (ωt + β) = ωCUm sin (ωt + β + π/2). Таким образом, синусоидальный П. т., проходящий через ёмкость, опережает по фазе напряжение на её зажимах на четверть периода, то есть φ = —π/2 (рис. 5). Эффективные значения в такой цепи связаны соотношением I = ωCU = U/xc, где xc = 1/ωС — ёмкостное сопротивление цепи. Векторные диаграммы наглядно иллюстрируют ход вычислений и служат для контроля над ними; построенные с соблюдением масштаба, они позволяют графически определить эффективное напряжение U в цепи и угол сдвига фаз φ. Несинусоидальность П. т. в электроэнергетических системах обычно нежелательна, и принимаются специальные меры для её подавления. Но в цепях электросвязи, в полупроводниковых и электронных устройствах несинусоидальность создаётся самим рабочим процессом. Если среднее за период значение тока не равно нулю, то он содержит постоянную составляющую. Для анализа процессов в цепях несинусоидального тока его представляют в виде суммы простых гармонических составляющих, частоты которых равны целым кратным числам основной частоты: I = i0 + I1m sin (ωt + α1)+ I2msin (2ωt + α2) +... + lkm sin (kωt + αk). Здесь I0 — постоянная составляющая тока, Iimsin (ωt + α1) — первая гармоническая составляющая (основная гармоника), остальные члены — высшие гармоники. Расчёт линейных цепей несинусоидального тока на основании принципа суперпозиции (наложения) ведётся для каждой составляющей (так как xL и xc зависят от частоты). Алгебраическое сложение результатов таких расчётов даёт мгновенное значение силы (или напряжения) несинусондального тока. Лит.: Теоретические основы электротехники, 3 изд., ч. 2, М., 1970; Нейман Л. Р., Демирчан К. С., Теоретические основы электротехники, т. 1—2, М.— Л., 1966; Касаткин А. С., Электротехника, 3 изд., М., 1974; Поливанов К. М., Линейные электрические цепи с сосредоточенными постоянными, М., 1972 (Теоретические основы электротехники, т. 1). А. С. Касаткин. Рис. 1. График периодического переменного тока i(t). Рис. 2. Графики напряжения u и тока i в цепи переменного тока при сдвиге фазы φ. Рис. 3. Схема и графики напряжения u и тока i в цепи, содержащей только активное сопротивление r. Рис. 4. Схема и графики напряжения u и тока i в цепи, содержащей только индуктивность L. Рис. 5. Схема и графики напряжения u и тока i в цепи, содержащей только ёмкость С. Рис. 6. Схема и векторная диаграмма цепи переменного тока с последовательным соединением индуктивности L, активного сопротивления r и ёмкости С. dic.academic.ru Для передачи и распределения электрической энергии преимущественно используется Переменный ток благодаря простоте трансформации его напряжения почти без потерь мощности (см. Передача электроэнергии, Электрическая цепь). Широко применяются трёхфазные системы Переменный ток (см. Трёхфазная цепь). Генераторы и двигатели Переменный ток по сравнению с машинами постоянного тока при равной мощности меньше по габаритам, проще по устройству, надёжнее и дешевле. Переменный ток может быть выпрямлен, например полупроводниковыми выпрямителями, а затем с помощью полупроводниковых инверторов преобразован вновь в Переменный ток другой, регулируемой частоты; это создаёт возможность использовать простые и дешёвые безколлекторные двигатели Переменный ток (асинхронные и синхронные) для всех видов электроприводов, требующих плавного регулирования скорости. Переменный ток широко применяется в устройствах связи (радио, телевидение, проволочная телефония на дальние расстояния и т. п.). Переменный ток создаётся переменным напряжением. Переменное электромагнитное поле, возникающее в пространстве, окружающем проводники с током, вызывает колебания энергии в цепи Переменный ток: энергия периодически то накапливается в магнитном или электрическом поле, то возвращается источнику электроэнергии. Колебания энергии создают в цепи Переменный ток реактивные токи, бесполезно загружающие провода и источник тока и вызывающие дополнительные потери энергии, что является недостатком передачи энергии Переменный ток За основу для характеристики силы Переменный ток принято сопоставление среднего теплового действия Переменный ток с тепловым действием постоянного тока соответствующей силы. Полученное таким путём значение силы Переменный ток I называется действующим (или эффективным) значением, математически представляющим среднеквадратичное за период значение силы тока. Аналогично определяется и действующее значение напряжения Переменный ток U. Амперметры и вольтметры Переменный ток измеряют именно действующие значения тока и напряжения. В простейшем и наиболее важном на практике случае мгновенное значение силы i Переменный ток меняется во времени t по синусоидальному закону: i = Im sin (wt + a), где Im - амплитуда тока, w = 2pf - его угловая частота, a - начальная фаза. Синусоидальный (гармонический) ток создаётся синусоидальным напряжением той же частоты: u = Um sin (wt + b), где Um - амплитуда напряжения, b - начальная фаза (рис. 2). Действующие значения такого Переменный ток равны: I = lm/ В цепи, не содержащей ни индуктивности, ни ёмкости, ток совпадает по фазе с напряжением (рис. 3). Закон Ома для действующих значений в этой цепи будет иметь такую же форму, как для цепи постоянного тока: I = U/r. Здесь r - активное сопротивление цепи, определяемое по активной мощности Р, затрачиваемой в цепи: r = P/I2. При наличии в цепи индуктивности L Переменный ток индуцирует в ней эдс самоиндукции eL= - L. di/dt = - wLlmcos (wt + a) = wLImsin (wt + a - p/2). Эдс самоиндукции противодействует изменениям тока, и в цепи, содержащей только индуктивность, ток отстаёт по фазе от напряжения на четверть периода, то есть j=p/2 (рис. 4). Действующее значение eL равно EL = IwL = IxL, где xL = wL - индуктивное сопротивление цепи. Закон Ома для такой цепи имеет вид: I = U/xL = U/wL. Когда ёмкость С включена под напряжение u, то её заряд равен q = Cu. Периодические изменения напряжения вызывают периодические изменения заряда, и возникает ёмкостный ток i = dq/dt = C×du/dt = (CUm cos (wt + b) = wCUm sin (wt + b + p/2). Таким образом, синусоидальный Переменный ток, проходящий через ёмкость, опережает по фазе напряжение на её зажимах на четверть периода, то есть j = -p/2 (рис. 5). Эффективные значения в такой цепи связаны соотношением I = wCU = U/xc, где xc = 1/wС - ёмкостное сопротивление цепи. Если цепь Переменный ток состоит из последовательно соединённых r, L и С, то её полное сопротивление равно Облегчение расчётов цепей синусоидальных Переменный ток достигается построением так называемых векторных диаграмм. Векторы синусоидальных тока и напряжения принято помечать точкой над буквенным обозначением ( Векторные диаграммы наглядно иллюстрируют ход вычислений и служат для контроля над ними; построенные с соблюдением масштаба, они позволяют графически определить эффективное напряжение U в цепи и угол сдвига фаз j. Для расчётов разветвленных цепей квазистационарного Переменный ток используют Кирхгофа правила. При этом обычно применяют метод комплексных величин (символический метод), который позволяет выразить в алгебраической форме геометрические операции с векторами Переменный ток и применить, таким образом, для расчётов цепей Переменный ток все методы расчётов цепей постоянного тока. Несинусоидальность Переменный ток в электроэнергетических системах обычно нежелательна, и принимаются специальные меры для её подавления. Но в цепях электросвязи, в полупроводниковых и электронных устройствах несинусоидальность создаётся самим рабочим процессом. Если среднее за период значение тока не равно нулю, то он содержит постоянную составляющую. Для анализа процессов в цепях несинусоидального тока его представляют в виде суммы простых гармонических составляющих, частоты которых равны целым кратным числам основной частоты: I = i0 + I1m sin (wt + a1)+ I2msin (2wt + a2) +... + lkm sin (kwt + ak). Здесь I0 - постоянная составляющая тока, Iimsin (wt + a1) - первая гармоническая составляющая (основная гармоника), остальные члены - высшие гармоники. Расчёт линейных цепей несинусоидального тока на основании принципа суперпозиции (наложения) ведётся для каждой составляющей (так как xL и xc зависят от частоты). Алгебраическое сложение результатов таких расчётов даёт мгновенное значение силы (или напряжения) несинусондального тока. Лит.: Теоретические основы электротехники, 3 изд., ч. 2, М., 1970; Нейман Л. Р., Демирчан К. С., Теоретические основы электротехники, т. 1-2, М.- Л., 1966; Касаткин А. С., Электротехника, 3 изд., М., 1974; Поливанов К. М., Линейные электрические цепи с сосредоточенными постоянными, М., 1972 (Теоретические основы электротехники, т. 1). А. С. Касаткин. Статья про слово "Переменный ток" в Большой Советской Энциклопедии была прочитана 53572 раз bse.sci-lib.com Если какой-либо источник тока вызывает в данном проводнике или в данной замкнутой цепи электродвижущую силу и эта электродвижущая сила непрерывно изменяется по величине и по направлению, т. е. представляется периодической функцией времени, то в рассматриваемом проводнике или в рассматриваемой замкнутой цепи появляется электрический ток, сила которого и направление изменяются также непрерывно со временем. Такой ток и носит название П. тока. Возникновение такого тока в проводнике осложняется явлениями индукции. В самом деле, вследствие непрерывного изменения силы П. тока возбуждается в проводнике, в котором происходит этот ток, особая электродвижущая сила, происходящая: 1) от самоиндукции, т. е. от индукции самого данного проводника с П. током, и 2) от индукции на этот проводник других проводников, находящихся вблизи первого проводника, так как в таких проводниках возникают также П. токи от индуктивного действия на них рассматриваемого проводника с П. током. Итак, полная электродвижущая сила, возбуждающая в какой-либо момент времени в данном проводнике электрический ток, представляет собой сумму электродвижущей силы источника тока и всех других электродвижущих сил, возникающих вследствие индукции. Обозначая через Е электродвижущую силу источника тока, причем, по условию, Е выражается какой-либо периодической функцией времени f(t), через L коэффициент самоиндукции данного проводника (см. Самоиндукция), через i силу тока в этом проводнике, через M1, M2, ... коэффициенты взаимной индукции данного проводника и других соседних с ним проводников, в которых силы токов суть i1, i2..., и пользуясь законами индукции токов, мы будем иметь для полной электродвижущей силы в данном проводнике выражение E = E — Ldi/dt — M1di1/dt — M2di2/dt... Обозначая сопротивление данного проводника через R, мы получаем по закону Ома для силы тока в этом проводнике выражение i = (E — Ldi/dt — M1di1/dt — M2di2/dt...)/R....
(1) Положим, что вблизи данного проводника не имеется никаких других проводников. В этом случае мы имеем i = (E — Ldi/dt)/R.... (2) Здесь по условию E = f(t), причем f(t) есть периодическая функция времени. Но по теореме Фурье всякая периодическая функция t может быть представлена в виде следующего ряда: f(t) = A + E0Sin(2πt/T — α) + E'0Sin(4πt/T — α') + E"0Sin(6πt/T — α") +... т. е. электродвижущая сила Е может быть рассматриваема как сумма постоянной электродвижущей силы А и электродвижущих сил, которые изменяются со временем по закону гармонического колебания (т. е. пропорционально синусам углов, непрерывно изменяющихся со временем) и которых периоды суть T, 1/2T, 1/3T..., а наибольшие величины суть Е0, Е'0, Е"0..., причем моменты, когда эти отдельные электродвижущие силы достигают своих наибольших величин или когда они обращаются в 0, различны, т. е. фазы этих электродвижущих сил неодинаковы. При таком характере электродвижущей силы E, действующей в проводнике, ток i, появляющийся в нем, может быть рассматриваем как ток, слагающийся из отдельных токов j, i0, i', i"..., которые возбуждаются в этом проводнике вследствие действия отдельных электродвижущих сил: A, E0Sin(2πt/T — α), E'0Sin(2πt/(1/2T) — α'), E"0Sin(2πt/(1/3T) — α"),... Наиболее простой и к тому же наиболее часто рассматриваемый в практике случай будет тот, когда электродвижущая сила, действующая в проводнике, выражается через E = E0Sin2πt/T... (3) т. е. эта электродвижущая сила изменяется со временем гармонически. Такую электродвижущую силу представляет электродвижущая сила, которая вследствие индукции появляется в какой-либо катушке, приготовленной из изолированной проволоки и приводимой в однородном магнитном поле в равномерное вращение около оси, лежащей в плоскости какого-либо оборота этой катушки и не совпадающей с направлением силовых линий поля. Такая же электродвижущая сила возбуждается и многими динамо-машинами П. тока. В данном случае мы получаем из выражения для i следующее дифференциальное уравнение: di/dt + (R/L)i = (E0/L)Sin2πt/T... (4) Интегрируя это уравнение и принимая во внимание, что при стационарном характере изменения величины электродвижущей силы и изменение силы тока должно быть также стационарного характера, получаем , причем tgθ = 2πL/TR... (6) или, обозначая через n число полных изменений электродвижущей силы в течение одной секунды, т. е. полагая n = t/T, имеем и tgθ = 2πnL/R... (6') R' = R(1 + 1/12(μ2l2p2/R2) — 1/180(μ4l4p4/R4) +... ), L' = l{A + μ(1/2 — 1/48(μ2l2p2/R2) + 13/8640(μ4l4p4/R4—... )}. Здесь μ обозначает магнитную проницаемость вещества проводника, l обозначает длину его, p = 2πn. Эти формулы значительно упрощаются, если положить, что n очень велико. В последнем случае мы получим . Возникновение в проводнике П. токов с очень большим числом перемен происходит в случае колебательных разрядов через этот проводник какого-либо наэлектризованного тела или конденсатора (см. Колебательный разряд). Такое же явление встречается при ударе молнии в громоотвод (см.). П. токи чрезвычайно большой частоты (например, токи Тесла) не вызывают никакого болевого ощущения в человеческом организме, тогда как П. токи со сравнительно небольшим числом n производят весьма сильные физиологические действия на нервную систему человека и животных. Вместо выражения (5') можно написать i = JSin(2πt/T — θ) = JSin2πt'/T... (7). Здесь J обозначает наибольшую величину силы П. тока. Из формулы (7) мы получаем для средней арифметической величины силы тока (im) (средней для всех значений i между 0 и J) выражение: . Средняя квадратичная сила П. тока (ie), или, по современной номенклатуре, действующая сила переменного тока (intensité efficace) получается по формуле Приборы, служащие для измерения силы П. тока (электродинамометры и амметры), обыкновенно и показывают величину ie, так как эти приборы основаны на действиях, пропорциональных квадрату силы тока. В самом деле, эти приборы основаны или на электродинамическом действии тока, или на тепловом его действии, или на действии тока на намагничиваемое им железо. Подобным же образом, как при определении im и ie, мы находим для средней арифметической величины (Еm) электродвижущей силы выражение Em = 2E0/π = 0,637E0 и для средней квадратичной величины (Еe ) или, по современной номенклатуре, для действующей электродвижущей силы Еe (force électromotrice efficace) выражение Средняя работа в единицу времени (Wm), необходимая для поддержания в проводнике П. тока, выражается через Такая же работа в течение единицы времени совершается в среднем и током. Эта работа будет очень мала, когда разность фаз θ близка к π/2. Положим, что вблизи данного неизменяемого проводника с П. током находится другой неизменяемый замкнутый проводник, в котором появляются индукционные токи, происходящие от действия на этот проводник данного проводника с П. током в нем. Обозначая через R1 и R2 сопротивления первого и второго проводников, через L1 и и L2 — коэффициенты самоиндукции этих проводников, через M — коэффициент взаимной индукции их, через Е = Е0Sin2πnt — электродвижущую силу в первом проводнике и через i1, i2 силы токов в них, мы получаем при помощи выражения (1) следующие дифференциальные уравнения: L1di1/dt + Mdi2/dt + R1i1— E0Sin2πnt = 0, L2di2/dt + Mdi1/dt + R2i2= 0. Отсюда находим . Итак, присутствие какого-либо замкнутого проводника вблизи данного проводника, в котором действует гармонически изменяющаяся электродвижущая сила, производит изменение кажущегося сопротивления этого проводника так, как будто истинное сопротивление (R1) этого проводника увеличивается, а коэффициент самоиндукции (L1) его уменьшается. На этом основано регулирование П. токов, употребляемых в электротехнике, при помощи вдвигания или выдвигания замкнутой катушки внутрь другой катушки, введенной в цепь регулируемого тока. Влияние самоиндукции цепи на силу тока в этой цепи, когда возбуждающая ток электродвижущая сила изменяется гармонически, т. е. выражается через Е = E0Sin2πnt, может быть уменьшено употреблением конденсатора. В самом деле, поместив в цепь П. тока конденсатор, емкость которого пусть будет обозначена через С, а разность потенциалов в какой-либо момент времени через V, мы получаем для силы тока в цепи выражения i = (E — Ldi/dt — V)/R... (9) и i = CdV/dt... (10). Так как при Е = E0Sin2πnt должно быть i = JSin(2πnt — θ), то получается V = — (J/2πnC)Cos(2πnt — θ) = —(1/4π2n2C)di/dt... (11). Итак, введение конденсатора с емкостью С в цепь П. (гармонически изменяющегося) тока производит уменьшение коэффициента самоиндукции цепи на величину 1/(4π2n2C), т. е. конденсатор, введенный в такую цепь, может быть уподоблен проводнику, сопротивление которого равно 0, а коэффициент самоиндукции равен — 1/(4π2n2C). Введение конденсатора в цепь изменяет также и разность фаз электродвижущей силы и тока, как это видно из формул (6') и (14). Введение конденсатора с емкостью С в ответвление цепи можно рассматривать, как помещение в это ответвление проводника, сопротивление которого равно 0, а коэффициент самоиндукции равен — 1/(4π2n2C). Если П., гармонически изменяющийся ток разветвляется в сети проводников, причем отдельные ветви обладают самоиндукцией и емкостью, то определение силы тока в какой-либо такой ветви может быть произведено следующим образом. Пусть сила тока в главной ветви, из которой ток разделяется на отдельные ветви, выражается через i = 2JCos2πnt = 2Jcospt... (15). Здесь введено обозначение p = 2πn. . Сила тока в какой нибудь ветви может быть выражена через . Коэффициенты KS и K'S для различных ветвей s находятся из обобщенных уравнений Кирхгофа, примененных к рассматриваемой сети проводников. А именно для каждой точки разветвлений, т. е. для каждой точки, в которой пересекаются проводники должно быть ΣSKS=0, ΣSK'S=0... (18) и для каждого замкнутого контура, состоящего из ветвей сети, должно быть ΣSKS WS=0, ΣSK'SWS=0... (19), причем . Здесь rS обозначает сопротивление ветви s, LS — коэффициент самоиндукции этой ветви и CS — емкость ее. Система П., гармонически изменяющихся токов с постоянной разностью фаз между двумя соседними токами носит название многофазного тока. Так, многофазный ток образуют n токов, силы которых выражаются через i1= J Sin2πnt i2= J Sin(2πnt + 2π/n) i3= J Sin(2πnt + 4π/n) ................... in—1 = J Sin(2πnt + (n—2)2π/n) in = J Sin(2πnt + (n—1)2π/n). Сумма этих токов в каждый отдельный момент равна 0, в чем легко убедиться, сложив вместе выражения i1, i2, i3,...in-1, in. Вследствие этого свойства такая система n токов, образуемая генератором, требует всего только n проводников, соединенных вместе их концами. Наиболее часто употребляется в электротехнике трехфазный ток, т. е. 3 тока, отличающиеся друг от друга по фазе на 120°. Такие многофазные токи употребляются главным образом для приведения во вращение электродвигателей с вращающимся магнитным полем (см. Электродвигатель). П. ток образует вокруг себя переменное магнитное поле, а потому если такой П. ток проходит по обмотке с сердечником из железа, то он возбуждает в этом железе П. магнитный поток и этот П. магнитный поток, период которого одинаков с периодом П. тока, вызывает индукционые токи, также П. и того же периода, в другой обмотке, окружающей собой сердечник первой и замкнутой какими-либо проводниками. Действующая электродвижущая сила в цепи этой второй обмотки может быть весьма различна, смотря по тому, каково отношение между числами оборотов проволоки в той и в другой обмотке. На этом начале устраиваются особые приборы, называемые трансформаторами и предназначаемые для превращения переменных токов малой силы и большого напряжения в П. токи большой силы и малого напряжения и обратно (см. Трансформатор). Благодаря возможности весьма легко, без употребления сложных и дорогостоящих приборов трансформировать П. токи из одних в другие, эти П. токи вошли в большое употребление на практике для целей электрического освещения и передачи электрической энергии на расстояние (см. Передача энергии). И. Боргман. dic.academic.ruПеременный ток. Переменный ток обозначение
Переменный электрический ток
Переменный ток Википедия
Постоянный ток Три примера переменных токов: Синусоидальный ток Пульсирующий ток, форма импульсов близка к пилообразной Случайно изменяющийся ток Общее понятие о переменном токе[ | код]
Переменный ток - это... Что такое Переменный ток?
в широком смысле Электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю. Периодом Т П. т. называют наименьший промежуток времени (выраженный в сек), через который изменения силы тока (и напряжения) повторяются (рис. 1). Важной характеристикой П. т. является его частота f — число периодов в 1 сек: f = 1/Т. В электроэнергетических системах СССР и большинства стран мира принята стандартная частота f = 50 гц, в США — 60 гц. В технике связи применяются П. т. высокой частоты (от 100 кгц до 30 Ггц). Для специальных целей в промышленности, медицине и др. отраслях науки и техники используют П. т, самых различных частот, а также импульсные токи (см. Импульсная техника). Для передачи и распределения электрической энергии преимущественно используется П. т. благодаря простоте трансформации его напряжения почти без потерь мощности (см. Передача электроэнергии, Электрическая цепь). Широко применяются трёхфазные системы П. т. (см. Трёхфазная цепь). Генераторы и двигатели П. т. по сравнению с машинами постоянного тока (См. Постоянный ток) при равной мощности меньше по габаритам, проще по устройству, надёжнее и дешевле. П. т. может быть выпрямлен, например полупроводниковыми выпрямителями, а затем с помощью полупроводниковых инверторов преобразован вновь в П. т. другой, регулируемой частоты; это создаёт возможность использовать простые и дешёвые безколлекторные двигатели П. т. (асинхронные и синхронные) для всех видов электроприводов, требующих плавного регулирования скорости. Переменный ток





Значение слова "Переменный ток" в Большой Советской Энциклопедии
Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под Переменный ток понимают периодический
ток, в котором среднее значение за период силы тока и напряжения равно нулю. Периодом Т Переменный ток называют наименьший промежуток времени (выраженный в сек), через который изменения силы тока (и напряжения) повторяются (рис. 1). Важной характеристикой Переменный ток является его частота f - число периодов в 1 сек: f = 1/Т. В электроэнергетических системах СССР и большинства стран мира принята стандартная частота f = 50 гц, в США - 60 гц. В технике связи применяются Переменный ток высокой частоты (от 100 кгц до 30 Ггц). Для специальных целей в промышленности, медицине и др. отраслях науки и техники используют П. т, самых различных частот, а также импульсные токи (см. Импульсная техника). 
Рис. 1. График периодического переменного тока i(t).  » 0,707 Im, U = Um/
» 0,707 Im, U = Um/ » 0,707 Um. Для синусоидальных токов, удовлетворяющих условию квазистационарности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифференциальной форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи Переменный ток индуктивности или (и) ёмкости между током i и напряжением u в общем случае возникает сдвиг фаз j = b - a, зависящий от параметров цепи (активного сопротивления r, индуктивности L, ёмкости С) и угловой частоты w. Вследствие сдвига фаз средняя мощность Р Т. т., измеряемая ваттметром, меньше произведений действующих значений тока и напряжения: Р = IU cosj.
» 0,707 Um. Для синусоидальных токов, удовлетворяющих условию квазистационарности (см. Квазистационарный ток; в дальнейшем будут рассматриваться только такие токи), справедлив Ома закон (закон Ома в дифференциальной форме справедлив и для неквазистационарных токов в линейных цепях). Из-за наличия в цепи Переменный ток индуктивности или (и) ёмкости между током i и напряжением u в общем случае возникает сдвиг фаз j = b - a, зависящий от параметров цепи (активного сопротивления r, индуктивности L, ёмкости С) и угловой частоты w. Вследствие сдвига фаз средняя мощность Р Т. т., измеряемая ваттметром, меньше произведений действующих значений тока и напряжения: Р = IU cosj. , где x = xL - xc = wL - 1/wC - реактивное сопротивление цепи Переменный ток Соответственно, закон Ома имеет вид:
, где x = xL - xc = wL - 1/wC - реактивное сопротивление цепи Переменный ток Соответственно, закон Ома имеет вид:  , а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления цепи к активному: tgj = х/r. В такой цепи при совпадении частоты w вынужденных колебаний, создаваемых источником Переменный ток, с резонансной частотой w0 = 1/
, а сдвиг фаз между током и напряжением определяется отношением реактивного сопротивления цепи к активному: tgj = х/r. В такой цепи при совпадении частоты w вынужденных колебаний, создаваемых источником Переменный ток, с резонансной частотой w0 = 1/ индуктивное и ёмкостное сопротивления равны (wL = 1/wС) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. Колебательный контур). В условиях резонанса напряжения на индуктивности и ёмкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи.
индуктивное и ёмкостное сопротивления равны (wL = 1/wС) и полностью компенсируют друг друга, сила тока максимальна и наблюдается явление резонанса (см. Колебательный контур). В условиях резонанса напряжения на индуктивности и ёмкости могут значительно (часто во много раз) превышать напряжение на зажимах цепи. ). Длины векторов обычно берутся равными (в масштабе построения диаграммы) действующим значениям I и U, а углы между векторами - равными сдвигам фаз между мгновенными значениями соответствующих величин. Алгебраическому сложению мгновенных значений синусоидальных величин одной и той же частоты соответствует геометрическое сложение векторов этих величин. На рис. 6 показана векторная диаграмма для цепи Переменный ток с последовательно соединёнными r, L, С. Мгновенное значение напряжения на зажимах этой цепи равно алгебраической сумме напряжений на активном и реактивном сопротивлениях: u = uL + ur + uc, следовательно,
). Длины векторов обычно берутся равными (в масштабе построения диаграммы) действующим значениям I и U, а углы между векторами - равными сдвигам фаз между мгновенными значениями соответствующих величин. Алгебраическому сложению мгновенных значений синусоидальных величин одной и той же частоты соответствует геометрическое сложение векторов этих величин. На рис. 6 показана векторная диаграмма для цепи Переменный ток с последовательно соединёнными r, L, С. Мгновенное значение напряжения на зажимах этой цепи равно алгебраической сумме напряжений на активном и реактивном сопротивлениях: u = uL + ur + uc, следовательно,  . При построении диаграммы исходным служит вектор тока, так как во всех участках неразветвлённой цепи ток один и тот же. Поскольку индуктивное напряжение опережает по фазе ток на p/2, а ёмкостное отстаёт от тока на p/2 (то есть они находятся в противофазе), при последовательном соединении они друг друга частично компенсируют.
. При построении диаграммы исходным служит вектор тока, так как во всех участках неразветвлённой цепи ток один и тот же. Поскольку индуктивное напряжение опережает по фазе ток на p/2, а ёмкостное отстаёт от тока на p/2 (то есть они находятся в противофазе), при последовательном соединении они друг друга частично компенсируют. Рис. 1. График периодического переменного тока i(t).
Рис. 1. График периодического переменного тока i(t).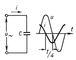 Рис. 5. Схема и графики напряжения u и тока i в цепи, содержащей только ёмкость С.
Рис. 5. Схема и графики напряжения u и тока i в цепи, содержащей только ёмкость С.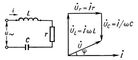 Рис. 6. Схема и векторная диаграмма цепи переменного тока с последовательным соединением индуктивности L, активного сопротивления r и ёмкости С.
Рис. 6. Схема и векторная диаграмма цепи переменного тока с последовательным соединением индуктивности L, активного сопротивления r и ёмкости С.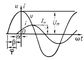 Рис. 2. Графики напряжения u и тока i в цепи переменного тока при сдвиге фазы j.
Рис. 2. Графики напряжения u и тока i в цепи переменного тока при сдвиге фазы j.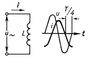 Рис. 4. Схема и графики напряжения u и тока i в цепи, содержащей только индуктивность L.
Рис. 4. Схема и графики напряжения u и тока i в цепи, содержащей только индуктивность L.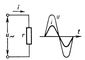 Рис. 3. Схема и графики напряжения u и тока i в цепи, содержащей только активное сопротивление r.
Рис. 3. Схема и графики напряжения u и тока i в цепи, содержащей только активное сопротивление r.Переменный ток - это... Что такое Переменный ток?
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: