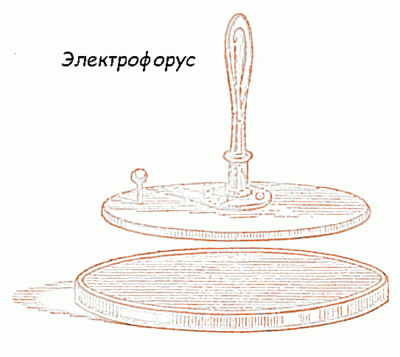
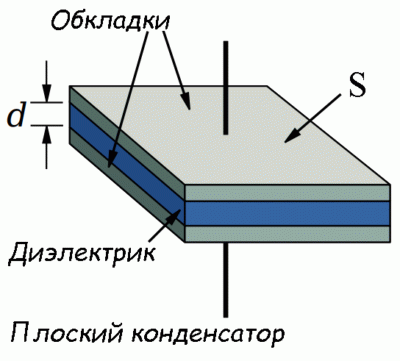
Для того чтобы уединенный проводник имел большую емкость, он должен обладать большими размерами. В жизни требуются тела малых и очень малых размеров, которые могли бы накопить существенный заряд, при небольших потенциалах (относительно других тел), то есть иметь большую емкость. Такие устройства называют конденсаторами. Причем проводники (обкладки конденсатора) должны иметь такую форму и быть расположены так по отношению друг к другу, что поле, создаваемое данной системой, было в основном расположено в ограниченной области пространства. Основной характеристикой конденсатора служит электроемкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок: q – величина заряда на обкладке; Емкость конденсатора зависит от формы, размеров, расположения обкладок и диэлектрической проницаемости диэлектрика ( Плоский конденсатор имеет обкладки в виде плоских проводящих пластин, разделенных слоем диэлектрика. Его емкость рассчитывают в соответствии с формулой: где Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляют как: где l – высота цилиндров; Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как: где так как Электрическую емкость для линии из двух проводов находят как: где d – расстояние между осями проводов; R – радиус проводов; l – длина линии. Еще одной важной характеристикой конденсатора является пробивное напряжение. Пробивное напряжение – это такая разность потенциалов между обкладками конденсатора, при которой происходит пробой диэлектрика. Эта величина зависит от толщины, свойств и формы диэлектрика, расположенного между обкладками конденсатора. ru.solverbook.com Плоский конденсатор – физическое упрощение, взявшее начало из ранних исследований электричества, представляющее собой конструкцию, где обкладки носят форму плоскостей и в любой точке параллельны. Люди ищут формулы, описывающие ёмкость плоского конденсатора. Читайте ниже любопытные и малоизвестные факты, сухие математические знаки также важны. Первым определил ёмкость плоского конденсатора Вольта. В его распоряжении ещё не было величины — разница потенциалов, именуемая напряжением, но интуитивно учёный правильно объяснил суть явления. Величину количества зарядов трактовал как объем электрического флюида атмосферы – не совсем правильно, но похоже на правду. Согласно озвученному мировоззрению ёмкость плоского конденсатора находится как отношение объёма накопленного электрического флюида к разнице атмосферных потенциалов: С = q/U. Формула применима к любому конденсатору, вне зависимости от конструкции. Признана универсальной. Специально для плоских конденсаторов разработана формула ёмкости, выраженная через свойства материала диэлектрика и геометрические размеры: В этой формуле через S обозначена площадь обкладок, вычисляемая через произведение сторон, а d – показывает расстояние между обкладками. Прочие символы – электрическая постоянная (8,854 пФ/м) и диэлектрическая проницаемость материала диэлектрика. Электролитические конденсаторы обладают столь большой ёмкостью по понятной причине: проводящий раствор отделен от металла крайне тонким слоем оксида. Следовательно, d оказывается минимальным. Единственный минус — электролитические конденсаторы полярные, их нельзя подключать в цепи переменного тока. С этой целью на аноде или катоде обозначены значками плюса или минуса. Плоские конденсаторы сегодня редко встречаются, это преимущественно плёночные микроскопические технологии, где указанный род поверхностей считается доминирующим. Все пассивные и активные элементы образуются через трафарет, образуя вид плёнок. Плоские индуктивности, резисторы и конденсаторы наносятся в виде токопроводящих паст. От материала диэлектрика зависит ёмкость, у каждого собственная структура. Считается, что аморфное вещество состоит из неориентированных диполей, упруго укреплённых на своих местах. При приложении внешнего электрического поля они обратимо ориентируются вдоль силовых линий, ослабляя напряжённость. В результате заряд накапливается, пока процесс не прекратится. По мере выхода энергии из обкладок диполи возвращаются на места, делая возможным новый рабочий цикл. Так функционирует плоский электрический конденсатор. Конденсатор для уроков Первым начал исследовать накопление заряда великий Алессандро Вольта. В докладе Королевскому научному обществу за 1782 год впервые озвучил слово конденсатор. В понимании Вольты электрофорус, представляющий две параллельные обкладки, выкачивал из эфира электрический флюид. В давнее время все познания сводились к мнению учёных, будто атмосфера Земли содержит нечто, не определяемое приборами. Присутствовали простейшие электроскопы, способные определить знак заряда и его наличие, не дававшие представления о количестве. Учёные просто натирали мехом поверхность тела и подносили для исследования в область влияния прибора. Гильберт показал, что электрические и магнитные взаимодействия ослабевают с расстоянием. Учёные примерно знали, что делать, но исследования не продвигались. Гипотеза об атмосферном электричестве высказана Бенджамином Франклином. Он активно исследовал молнии и пришёл к выводу, что это проявления прежней единой силы. Запуская воздушного змея в небо, он соединял игрушку шёлковой нитью с землёй и наблюдал дуговой разряд. Это опасные опыты, и Бенджамин многократно рисковал собственной жизнью ради развития науки. Шёлковая нить проводит статический заряд — это доказал Стивен Грей, первый собравший в 1732 году электрическую цепь. Уже через 20 лет (1752 год) Бенджамин Франклин предложил конструкцию первого громоотвода, осуществлявшего молниезащиты близлежащих построек. Только вдуматься! – прежде любой ожидал, что дом сгорит от случайного удара. Бенджамин Франклин предложил один вид заряда называть положительным (стеклянный), а второй отрицательным (смоляной). Так физики оказались введены в заблуждение относительно истинного направления движения электронов. Но откуда возьмётся иное мнение, когда в 1802 году на примере опытов россиянина Петрова увидели, что на аноде образуется ямка? Следовательно, положительные частицы переносили заряд на катод, но в действительности это оказались ионы воздушной плазмы. К началу исследования Вольтой электрических явлений уже известны статические заряды и факт наличия у них двух знаков. Люди упорно считали, что «флюид» берётся из воздуха. На эту мысль натолкнули опыты с натиранием янтаря шерстью, не воспроизводимые под водой. Следовательно, логичным стало предположить, что электричество может происходить исключительно из атмосферы Земли, что, конечно же, неверно. К примеру, многие растворы, исследованные Хампфри Дэви, проводят электрический ток. Причина, следовательно, иная – при натирании янтаря под водой силы трения снижались в десятки и сотни раз, а заряд рассеивался по объёму жидкости. Следовательно, процесс лишь оказывался неэффективным. Сегодня каждый добытчик знает, что нефть электризуется трением о трубы без воздуха. Следовательно, атмосфера для «флюида» не считается обязательным компонентом. Столь систематизированные, но в корне неверные толкования не остановили Вольту на исследовательском пути. Он упорно изучал электрофорус, как совершенный генератор того времени. Вторым был серный шар Отто фон Герике, изобретённый на век раньше (1663 год). Его конструкция мало менялась, но после открытий Стивена Грея заряд начали снимать при помощи проводников. К примеру, в электрофорной машине применяются металлические гребёнки-нейтрализаторы. Долгое время учёные раскачивались. Электрофорная машина 1880 года вправе считаться первым мощным генератором разряда, позволявшим получить дугу, но истинной силы электроны достигли в генераторе Ван де Граафа (1929 год), где разница потенциалов составила единицы мегавольта. Для сравнения — грозовое облако, согласно данным Википедии, обнаруживает потенциал относительно Земли в единицы гигавольт (на три порядка больше, чем в человеческой машине). Суммируя сказанное, с определённой долей уверенности скажем, что природные процессы используют в качестве принципа действия электризацию трением, влиянием и прочие виды, а мощный циклон считается самым большим из известных плоских конденсаторов. Молния показывает, что случается, когда диэлектрик (атмосфера) не выдерживает приложенной разницы потенциалов и пробивается. В точности аналогичное происходит в плоском конденсаторе, созданном человеком, если вольтаж оказывается непомерным. Пробой твёрдого диэлектрика необратим, а возникающая электрическая дуга часто служит причиной расплавления обкладок и выхода изделия из строя. Итак, Вольта взялся за исследование модели природных процессов. Первый электрофорус появился в 1762 году сконструированный Йоханом Карлом Вильке. По-настоящему популярным прибор становится после докладов Вольты Королевскому научному обществу (середина 70-х годов XVIII века). Вольта дал прибору нынешнее название. Вид электрофоруса Электрофорус способен накапливать электростатический заряд, образованный трением резины куском шерсти. Состоит из двух плоских, параллельных друг другу обкладок: Принцип действия плоского конденсатора уже понятен. Оператор трёт резину шерстью, оставляя на ней отрицательный заряд. Сверху кладётся кусок металла. Из-за значительной шероховатости поверхностей они не соприкасаются, но находятся на расстоянии друг от друга. В результате металл электризуется влиянием. Электроны отталкиваются поверхностным зарядом резины и уходят на внешнюю плоскость, где оператор их снимает через заземлитель лёгким кратковременным прикосновением. Низ металлической обкладки остаётся заряженным положительно. При расстыковке двух поверхностей этот эффект сохраняется, в материале наблюдается дефицит электронов. И заметно искру, если дотронуться до металлической обкладки. Этот опыт допускается на единственном заряде резины проделывать сотни раз, её поверхностное статическое сопротивление крайне велико. Это не даёт заряду растекаться. Демонстрируя описанный опыт, Вольта привлёк внимание научного мира, но исследования не двигались вперёд, если не считать открытий Шарля Кулона. В 1800 году Алессандро даёт толчок развитию изысканий в области электричества, изобретя знаменитый гальванический источник питания. Электрофорус представляет собой первый из сконструированных плоских конденсаторов. Его обкладки способны хранить только статический заряд, иначе наэлектризовать резину невозможно. Поверхность чрезвычайно долго хранит электроны. Вольта даже предлагал снимать их пламенем свечи через ионизированный воздух или ультрафиолетовым излучением Солнца. Сегодня каждый школьник знает, что явление проделывается водой. Правда, электрофорус потом потребуется высушить. В современном мире нижней обкладкой служит тефлоновое покрытие или пластик. Они хорошо набирают статический заряд. Диэлектриком становится воздух. Чтобы перейти к конструкции современного конденсатора, нужно обе обкладки сделать металлическими. Тогда при возникновении на одной заряда электризация распространится на вторую, и если другой контакт заземлён, накопленная энергия хранится определённое время. Конструкция в деталях Запас электронов напрямую зависит от материала диэлектриков. К примеру, среди современных конденсаторов встречаются: В эти названия заложен материал диэлектрика. От состава зависит напрямую ёмкость, способная увеличиваться многократно. Роль диэлектриков объяснялась выше, их параметры определяются непосредственно строением вещества. Однако многие материалы, обладающие высокими характеристиками, использовать не удаётся по причине их непригодности. К примеру, вода характеризуется высокой диэлектрической проницаемостью. vashtehnik.ru Электроемкость конденсатора – физическая величина, характеризующая процесс заряда проводников, разделенных слоем диэлектрика. Используется многочисленными математическими расчетами, маркируется на корпусе изделия. Электроемкость конденсатора принято выражать через запасаемый заряд q при приложенном напряжении U подобным образом: C = q/U. Происхождение формулы — загадка. Известно только: из теоремы Гаусса по напряженности электрического поля найдем электроемкость конденсатора. Кто провел расчет, нигде не говорится. Физическая величина фарад изначально в системе СГС отсутствовала, в 1861 году ввела специальная комиссия, сформированная физиками. По отдельным сведениям, впервые электроемкость конденсатора определил введший термины в обиход. Подразумеваем Алессандро Вольту. Поздние 70-е (XVIII века) ученый уделил исследованиям вопроса, установил: электроемкость можно выразить через накапливаемый заряд, приложенное к электродам напряжение. Вдобавок удаётся часто встретить формулу электроемкости плоского конденсатора: Авторы избегают судить, кто занимался расчетами выражения. Рассуждая логически, мало кого интересовала электроемкость плоского конденсатора до появления на свет изобретения Полака. Лейденские банки по-другому распределяют заряд. Рассуждения приводят к началу XX века. Возможно, вопросом занимались Тесла, Герц. С меньшей вероятностью – Попов. Фамилии названы по критериям заинтересованности переменным током. Тесла изучал вопросы безопасности электричества, передачи на расстояние, конструировал двигатели. Герц и Попов исследовали антенны, заведомо настраиваются на некую длину волны, которую проще получить, применяя колебательный контур. Следовательно, ученые обязаны иметь представление об электроемкости конденсатора, катушках индуктивности. Джеймс Максвелл, лорд Кельвин, Вильгельм Вебер много внимания уделяли совершенствованию единых систем измерения физических величин. Вероятно, кто-то приложил руку к исследованию конденсаторов. Ясно одно – в мировой истории естественных наук масса белых пятен, когда дело касается русскоязычных источников. Портал ВашТехник одним из первых начнёт публиковать новейшие исследования в области правильного понимания произошедших событий. Нетерпеливым читателям докладываем: Алессандро Вольта ввел собственно термин емкости. Неизвестно точно, употреблял ли кто раньше, но в своей работе итальянский ученый, называя электрофорус конденсатором, одновременно применяет к нему термин емкости. Как сосуду, куда можно «налить» заряд из емкости. Конденсатором зовет за схожесть процесса с осаждением паров: понемногу наберем произвольное количество электричества. По большому счету, это верно. Исторически первым конденсатором считают лейденскую банку. Поныне ходят споры, кто изобрел прибор, поскольку оба ученых, увлеченных событиями, избегали ведения аккуратных записей. Бесспорно одно – электроемкость прибора измерить было нельзя, отсутствовало соответствующее понятие «электроемкость конденсатора». Скрин печатного варианта трактата Вольты, 1782 год Придумавший термин бессилен произнести слово раньше, нежели Алессандро Вольта в 1782 году, докладывая Королевскому Научному обществу изыскания в области электростатики, чтобы понять, откуда берется электричество. Известно, в течение следующих пяти лет Луиджи Гальвани откроет «животное электричество», приведшее Вольту прямиком к созданию первого элемента питания. Докладывая обществу, молодой ученый лишен упомянутых знаний, светило пытается понять, откуда появляется заряд. Рассуждает приблизительно так: «К настоящему времени немало свидетельств существования атмосферного электричества. Люди бессильны найти следы присутствия. Вероятно, означает: созданные электроскопы слишком слабы, неспособны уловить столь тонкую материю. Следовательно, требуется найти способ забрать из воздуха флюиды». Выполняя сказанное, Алессандро Вольта предлагает приспособление, называемое электрофорусом (не путать с электрофорной машиной). Прибор захватывает флюиды атмосферного проводника (воздуха). Принцип служения Вольте напоминает процесс конденсации: собирает электричество. Запад электрофорус называет генератором емкостного типа. Указанное выше позволяет полагать: подобное определение прилепилось благодаря написанному Английскому Королевскому обществу Вольтой. Устройство придумано другим человеком – шведским физиком Джоном Кларком Вилке. Случилось двумя десятилетиями ранее – 1762 год. Ныне считается, популярность прибору придал Вольта, называя любимца вечным генератором электричества. Тоже по сути правильно, тереть резину можно тысячелетиями. Больше «конденсатор» напоминает (см. рис.) здоровенную печать. Сверху, помимо основной центральной ручки, стоит боковая – снятия отрицательного потенциала. Видим три слоя: Внешний вид электрофоруса Начав работы, нужно убрать «печать», натереть резину шерстью. Затем гладкий диск ставится обратно. Площадь соприкосновения с резиной невелика из-за присутствующих шероховатостей, положительный заряд приобретается нескоро. Нужно выждать. Оператор на короткий миг заземляет крышку боковой ручкой, снимая отрицательный заряд, снизу остается положительный. Прикасаясь одной рукой к металлу, можно слышать хорошо различимый треск. Резина после поднятия крышки несет избыток электронов, позволяющий повторить опыт несколько раз (верится с трудом, некоторые источники говорят о сотне повторений). Разнимая тела, резким движением потянув изолирующую рукоятку, оператор получает статическое электричество. Изобретение революционное, примечательно, появилось в считанные годы после отмены закона охоты на ведьм. По заявлению Вольты, круг резины делается по возможности тонким, в пределах 50-й доли дюйма. Удается получить наилучший результат. Лист металла фактически становится пластиной. В противном случае долго придётся ждать наполнения объема проводника. В простонародье «конденсатор» называют резиновым пирогом. Пирогом, покрытым металлической начинкой. Действительно ли электрофорус является неисчерпаемым источником энергии? В идеальных условиях, хотя верится с трудом. Отрицательный заряд резины поляризует металлическую пластину, создавая некий потенциал. Вытесненные на внешнюю поверхность электроны снимаются прикосновением заземлителя. Остается разнять составные части электрофоруса. Уничтожив положительный заряд прикосновением, услышав звук проскочившей искры, можно заново начинать опыт. Электрофорус действительно напоминает конденсатор. После снятия лишнего отрицательного заряда превращается фактически в упомянутый прибор. Долго храниться конденсатор не может, поскольку электроны с резины понемногу будут стекать на металл. Устройство разрядится. Фактически резина, металл отделены друг от друга воздухом, служащим диэлектриком. Вместо резины используем различные полимеры, например, Тефлон. Осталось заметить: во времена Вольты не знали методов избавления резины от статического заряда. «Обкладка» конденсатора могла долгое время хранить груз электронов. Вольта предлагает для разрядки поместить образец под солнечные лучи, либо поводить рядом горящей свечой. Через ионизированное пламя электроны покидают конденсатор. Сегодня понятно, достаточно вымыть резину, чтобы следов не осталось статического напряжения. Для работы потребуется вновь высушить. Считается, что Феликс Савари обнаружил колебания резонансного контура. Разряжая лейденскую банку через витую нить меди, наблюдал беспорядочное снование стрелки компаса. 1826 год, когда Англия, Франция, Германия, частично Италия лихорадочно исследовали новое явление, привнесенное в научный мир Эрстедом. Историю создания лейденской банки можно прочитать в соответствующем обзоре. Следует сказать, никто не пытался толком понять, какова электроемкость конденсатора. Не нужно по очевидным соображениям: лейденскую банку преимущественно использовали научные круги, решая специфические задачи. Опыт Феликса Савари надолго остался без внимания… В 1842 году колебательным контуром, электроемкостью конденсатора занялся наш старый знакомый, сэр Джозеф Генри, изобретатель электромагнитного реле, любитель телеграфа. Изложил письменно после опробования заметок Савари практикой: «Аномалия, остающаяся столь долго без объяснения, которая на первый взгляд представляется существующей наперекор нашей теории электричества и магнетизма, после тщательного изучения мною отнесена к доселе неизведанным явлениям. Разряд происходит странно (вразрез теории Франклина), ощущение, что, выходя из банки, флюид начинает странствовать взад-вперед. Увиденное принуждает признать: процесс начинается нормальным образом, затем происходит несколько смен направлений, каждый раз амплитуда становится меньше, пока движения затухнут вовсе. Судя по всему, феномен сегодня не может быть объяснен, физики встречались с ним (Савари), но оказались бессильны». Очевидно, ученого совершенно не интересует электроемкость конденсатора – мысли поглощены аномалией, которую хотелось бы разведать. Пятью годами позже, ознакомившийся с отчетом Генри физик Гельмгольц на встрече Физического общества Берлина, говорит: «Проводя электролиз, заметил необычные колебания. Такое ощущение, процесс колебаний продолжается, пока само vis viva не исчезнет навсегда, поглощенное суммарным сопротивлением цепи. Создается впечатление, по контуру текут два тока противоположных направлений, верх берет то один, то другой». Конец спорам положил знаменитый Вильям Томсон, нареченный лорд Кельвин. Математически исследовав процесс, заявил: в цепи очевидно присутствуют две вещи: электроемкость конденсатора и индуктивность свернутой медной проволоки. Работа On Transient Electric Currents стала классической. Хотя лорд Томсон зовет индуктивность электродинамической емкостью, смысл формулы однозначный. Ученый первым заявил: энергия передается меж конденсатором и катушкой индуктивности, постепенно затухая на активном сопротивлении цепи. Формула, приведенная на рисунке, дана в современных величинах, обозначения стандартные. С – электроемкость конденсатора, L – индуктивность катушки, q – величина заряда, I – ток цепи. Прочие символы относятся к операциям дифференцирования. Термин индуктивность введен намного позже – в 1886 году Оливером Хэвисайдом. Формула резонансной частоты, зависящей от электроемкости конденсатора и индуктивности катушки, выведена Джеймсом Максвеллом в 1868 году. vashtehnik.ru Одна из характеристик конденсатора называется емкость. Способность проводника и окружающей его среды накапливать электрическое поле называется электрической емкостью. где Q - величина электрического заряда в кулонах [Кл]; Δφ - разность потенциалов между обкладками конденсатора или разность потенциалов между проводником и средой в вольтах [В]. Так же емкость плоского конденсатора можно рассчитать по формуле: Где ε0 = 8,85 *10-12- относительная диэлектрическая проницаемость; Где ε - диэлектрическая проницаемость среды (диэлектрика) между обкладками; S - площадь обкладки конденсатора; d - расстояние между обкладками конденсатора. Где ε0 = 8,85 *10-12- относительная диэлектрическая проницаемость; Где ε - диэлектрическая проницаемость среды (диэлектрика) между проводниками; L - длина проводника; R1 - внутренний радиус провода; R2 - внешний радиус оплетки. www.kurstoe.ru
"Радиолюбитель", №3, март, 1925 год, стр. 63-64
С. И. Шапошников Известно, что существуют некоторые приборы, в которых можно накапливать или собирать электричество.
Такие приборы называются конденсаторами.
Возьмем несколько различных конденсаторов и присоединим их параллельно, например, к батарее в 80 вольт напряжением. Обкладки конденсаторов сейчас же получат заряды от полюсов батареи и зарядятся до того же напряжения, что и у батареи.
Отсоединяя теперь поочередно конденсаторы, не касаясь их контактов руками, будем касаться ими до зажимов чувствительного прибора. При этом мы заметим следующее: в момент присоединения конденсатора к прибору проскочит искорка, сопровождаемая более или менее громким треском, и прибор даст мгновенное отклонение стрелки 1). Так как эти отклонения будут различны, мы заключаем, что заряды разных конденсаторов, полученные от одной и той же батареи, будут различны, т.-е. одни конденсаторы получат большее количество электричества, другие — меньшее.
Электроемкостью, или, как говорят чаще, емкостью конденсатора, называется способность его воспринимать большее или меньшее количество электричества.
Для измерения емкостей установлена единица, т.-е. определенная емкость, называемая фарадой.
Емкостью в 1 фараду обладает такой конденсатор, который, будучи заряжен до напряжения в один вольт, при разряде даст ток, средняя величина которого будет равна одному амперу, при длительности прохождения тока в одну секунду.
Фарада — емкость весьма большая, почему ее разделили на миллион частей, называя такую единицу микрофарадой.
Но для целей радиотехники часто и микрофарада является слишком большой. Поэтому чаще пользуются третьей единицей, называемой сантиметром.
Микрофарада равна девятистам тысячам сантиметров.
Деля число сантиметров на 900.000, мы превратим емкость, выраженную в сантиметрах, в микрофарады. А разделив число микрофарад на 1.000.000, мы выразим ту же емкость в фарадах.
Простейший конденсатор состоит из двух пластин любого металла, разделенных одна от другой слоем любого непроводника или изолятора, или жке, как иначе его называют, диэлектрика.
Рис. 1. Параллельное соединение конденсаторов. Пусть мы имеем два совершенно одинаковых конденсатора с одинаковой емкостью — С1 и С2. Соединим их параллельно к батарее Б (рис. 1). Очевидно, что емкость такой соединенной группы будет вдвое больше, чем емкость одного конденсатора, так как два конденсатора, при заряде, получат две порции электричества.
Что у нас изменилось, когда мы присоединили второй конденсатор? Диэлектрик остался прежний, толщина его тоже.
Изменилась величина пластин, или, как их называют, обкладок — вдвое. Во столько же раз изменилась и емкость системы. Поэтому, если взять такой же диэлектрик, как у двух первых конденсаторов, но обкладки его увеличить по площади вдвое, то мы получим один конденсатор, но с емкостью вдвое большей.
Итак: емкость конденсатора зависит от величины обкладок. Чем площадь обкладок меньше, тем меньше емкость конденсатора. Чем площадь обкладок больше, тем больше емкость конденсатора.
Рис. 2. Последовательное соединение конденсаторов. Теперь соединим два одинаковых конденсатора последовательно, как показано на рис. 2-a. Измерение показывает, что емкость такой группы стала вдвое меньше, чем у каждого конденсатора в отдельности. Что же у нас изменилось?
Будем сближать оба конденсатора их внутренними обкладками. Оказывается, что от этого емкость группы изменяться не будет. Она будет оставаться все время вдвое меньшей, чем емкость одного конденсатора. То же будет и тогда, когда внутренние обкладки конденсаторов соединятся между собой, как это изображено на рис. 2-б. И, наконец, то же самое будет, если мы выдернем внутренние обкладки, как это показано на рис. 2-в. Теперь нам ясно. что у нас изменилось: толщина диэлектрика. Она увеличилась вдвое, поэтому емкость уменьшилась вдвое.
Итак: емкость конденсатора уменьшается с увеличением толщины диэлектрика и, наоборот, увеличивается с уменьшением толщины диэлектрика, при условии, что площадь обкладок остается прежней.
Теперь возьмем конденсатор, у которого диэлектрик — воздух. Такой воздушный конденсатор имеет некоторую емкость. Вставим в промежуток между обкладками его диэлектрик из парафиновой бумаги такой же толщины, какой был слой воздуха. Измерение доказывает, что емкость парафинового конденсатора увеличилась в 2,2 раза. Если парафин заменить стеклом такой же толщины, емкость увеличится в 5—6 раз против емкости воздушного конденсатора.
Следовательно, емкость конденсатора зависит от химических свойств диэлектрика.
Величину, показывающую, во сколько раз увеличилась емкость воздушного конденсатора при замене воздуха каким-либо диэлектриком называют диэлектрической постоянной этого диэлектрика.
Диэлектрическую постоянную будем обозначать буквой К.
Все вышеприведенные рассуждения можно свести в формулу, по которой легко производить расчет емкости разных конденсаторов.
В этой формуле буквой С обозначается, как принято, емкость; К — диэлектрическая постоянная; S — площадь одной обкладки, выраженная в квадратных сантиметрах, и d — толщина диэлектрика, выраженная в сантиметрах (длины): π — число, равное 3,14.
Для лучшего усвоения приведем
Пример 1. Конденсатор стеклянный. Толщина стекла 3 мм. Обкладок две, каждая 15 см. длины и 10 см ширины.
По таблице № 1 диэлектрическая постоянная для стекла K = от 4 до 8; примем за среднее K = 6. Площадь обкладки S = 15 × 10 = 150 кв. см.; толщина стекла d = 3 мм., что переводим в сантиметры и получим: d = 0,3 см. По формуле получим:
Пример 3. Стеклянная лейденская банка (см. рис. 3). Внутренний диаметр D = 5 см., высота обкладок h = 10 см; толщина стекла d = 2 мм. Так как наружная обкладка больше внутренней, то мы и привели внутренние размеры банки, так как при неравных по площади обкладках надо измерить меньшую из них.
Рис. 3. Лейденская банка. Попрежнему: K = 6; d = 0,2 см. Площадь дна определяется по формуле, по которой рассчитывается сечение проводников (см. стр. 17).
Площадь цилиндрической части обкладки будет:
S = π · d · h = 3,14 · 5 · 10 = 157 кв. см. Площадь всей внутренней обкладки будет: 19,6 + 157 = 176,6 кв. см.
Пример 3. Конденсатор парафиновый. Число пластин 10. Размер станиолевых листочков 3 × 9 см.
Рис. 4. Как определяется площадь пластины. Для определениия толщины листка парафиновой бумаги, разрежем один листок на части, зажмём их между двумя досочками и измерим, сколько листочков приходится на 1 мм. Предположим 13. Тогда толщина диэлектрика будет ¹/13 мм, что, превратив в сантиметры, получим ¹/130 см. K — для парафина по табл. № 1 будет = 2,2. За площадь одного листа станиоля надо принять ту часть его, которая перекрывается следующим листком (см. рис. 4). Следовательно, длина его будет, напр., 6 см. Площадь одного листка будет 3 × 6 = 18 кв. см. Если бы листков было 2, то площадь обкладки равнялась бы 18 кв. см. Если листков взять 3 (см. рис. 4), то листок второй дает с первым площадь 18 кв. см., но он же дает такую же площадь и с третьим, следовательно, при 3 листках площадь будет вдвое больше и т. д. При десяти листках площадь будет в 9 раз больше. Следовательно, S = 9 . 18 = 162 кв. см., откуда:
Для подсчета емкости конденсатора, состоящего из нескольких пластин, можно воспользоваться и такой формулой.
где S1 — площадь одной пластины, а n — число пластин. В последнем примере S1 = 18 кв. см.; n = 10, следов., n — 1 = 10 — 1 = 9, тогда по форм. (2) имеем:
т.-е. такой же результат, как и раньше.
Разобранные три примера поясняют все случаи расчетов емкости различных типов конденсаторов.
Мы умеем рассчитать конденсатор. Это важно при постройке его, чтобы иметь представление каких размеров его строить для данной емкости.
Но мы видели, что стекло различных сортов имеет диэлектрическую постоянную от 4 до 8. То же бывает и с другими электриками. Значит, мы можем произвести ошибку из-за величины K. Но, кроме того, мы можем ошибиться и при определении толщины диэлектрика или размеров пластинок. Следовательно, нам надо проверить наш расчет, произведя измерение емкости конденсатора, к чему мы и перейдем, дав представление о том, как ведет себя конденсатор в разных электрических цепях.
1) Чтобы опыт был заметен, емкости д.б. достаточно большие, напр. микрофарады, а прибор — миллиамперметр.
(назад)
sergeyhry.narod.ru Итак, теория Гельмгольца находится в качественном согласии с рядом экспериментальных фактов. Именно поэтому при рассмотрении свойств двойного слоя часто прибегают к формуле плоского конденсатора. Вместе с тем теория Гельмгольца не охватывает всей совокупности экспериментальных фактов. Так, например, согласно этой [c.104] Итак, теория Гельмгольца находится в качественном согласии с рядом экспериментальных фактов. Именно поэтому при рассмотрении свойств двойного слоя часто прибегают к формуле плоского конденсатора. [c.108] Гельмгольц предположил,что двойной слой ведет себя как обыкновенный плоский конденсатор, так что его потенциал X, может быть определен из формулы для потенциала плоского конденса- [c.208] Обычно поверхностный потенциал не пытаются интерпретировать как потенциал одной поверхпости. Как правило, вместо этого рассматривают разность поверхностных потенциалов чистой подложки и подложки, покрытой пленкой. Эту разность АУ приписывают пленке и качественно рассматривают ее как аналог конденсатора. Разность потенциалов АУ между двумя проводящими пластинами, удаленными друг от друга на расстояние й и несущими заряд плотностью о, в соответствии с формулой, приписываемой Гельмгольцу, равна [c.99] В теории Гельмгольца не учитывается, что свойства двойного электрического слоя изменяются с концентрацией электролита и его температурой. Гуи (1910) и Чанман (1913) попытались устранить этот недостаток теории Гельмгольца и связать плотность заряда в двойном слое с составом раствора. Они отметили, что предполагаемое в теории конденсированного двойного слоя строго фиксированное расположением ионов в действительности невозможно, так как, помимо электростатических сил, возникающих между металлом и ионами, на последние должны действовать также силы теплового молекулярного движения. При наложении этих двух сил ионы в растворе должны распределяться относительно поверхности металла диффузно — с убывающей при удалении от нее объемной плотностью заряда подобно тому, как меняется с высотой плотность воздушной атмосферы. При таком строении двойного электрического слоя для выражения связи между потенциалом и плотностью заряда уже нельзя воспользоваться формулой плоского конденсатора. По закону электронейтральности можно написать, что [c.269] Это выражение аналогично формуле Гельмгольца для плоского конденсатора (см. разд. 1П-ЗБ), поэтому при малых потенциалах диффузный двойной слой можно рассматривать как электрический конденсатор с расстоянием между пластинами, равным 1/х. При больших потенциалах о резко увеличивается с ростом и емкость двойного слоя также возрастает. [c.165] Хотя Гельмгольц и прямо заявляет о диффузном характере двойного слоя, он все же использует в своих вычислениях модель плоского конденсатора. Теория распределения заряда потенциала в диффузном слое принадлежит Гуи. Распространенная фор-мула для вычисления толщины двойного слоя вытекает также из теории сильных электролитов Дебая — Гюккеля. Поэтому ее обычно называют формулой Дебая — Гюккеля. [c.159] В простейшей модели двойного электрического слоя, называемой моделью Гельмгольца, заряд +Q равномерно распределен по плоской поверхности площадью А и удален на расстояние от аналогичной плоскости с зарядом —Q, Записывая а = Q/A для поверхностной плотности заряда и используя формулу для плоского конденсатора, получим разность потенциалов двойного электрического слоя [c.41] Еще одним усложнением теории двойного слоя является выделение в слое Штерна так называемой внутренней плоскости Гельмгольца (здесь используется формула конденсатора Гельмгольца). Эта плоскость располагается на поверхности щтерновского слоя адсорбированных ионов и внешней плоскости Гельмгольца, проходящей через центры следующего слоя ионов, с которого начинается диффузный слой. Внутренняя и внешняя плоскости Гельмгольца, сокращенно обозначаемые как ШР и ОНР соответственно (рис. 1У-2), дальше рассматриваются в разд. 1У-9В. В серии статей Левина и др. [114] исследовано влияние дискретности заряда, приводящее к тому, что локальный потенциал Штерна, который определяет адсорбцию ионов, фактически не равен среднему потенциалу и отличается от последнего на величину потенциала самих ионов , что, в частности, приводит к взаимному отталкиванию адсорбированных ионов. Теория предсказывает, что при увеличении г1зо потенциал ОНР может проходить через максимум. Рассмотренный эффект действительно проявляется в электрокапиллярных явлениях (см. также упражнение 6). [c.171] Строение двойного электрического слоя. Основываясь на экспериментальных данных, полученных Квинке при изучении электрокинетических явлений, Г. Гельмгольц предложил первую модель двойного электрического слоя. Согласно воззрениям Гельмгольца, в дальнейшем развитым М. Смолуховским и Ж. Перреном, двойной электрический слой рассматривается как заряженный плоский конденсатор. На поверхности находится слой ионов, называемых потенциалобразующими, а на некотором расстоянии от нее в жидкой фазе находятся, удерживаемые силой электростатического притяжения, ионы противоположного знака, называемые противоионами. Модель Квинке — Гельмгольца предполагает, что расстояние между плотным слоем противоионов и слоем потенциалопределяющих ионов повсюду одинаково. По условию электронейтральности удельные поверхностные заряды (поверхностные плотности зарядов) обенх составляюш,их частей двойного электрического слоя должны быть равны по абсолютной величине д+=д . Скачок потенциала для модели Квинке — Гельмгольца рассчитывается по известной формуле для плоского конденсатора 9=СД >1, в которой С—емкость плоского конденсатора на единицу площади, причем С = еео- - (еео — [c.87] Теория Гельмгольца—Перрена. Согласно этой теории двойнЪй слой представляется как бы плоским конденсатором, одна обкладка которого связана непосредственно с поверхностью твердого тела (стенкой), а другая обкладка, несущая противоположный заряд, находится в жидкости на очень малом расстоянии от первой. Потенциал в таком двойном слое, равно как и потенциал в плоском конденсаторе, очевидно, должен падать весьма круто (по прямой), а значение поверхностного заряда а будет определяться известной из физики формулой [c.175] Модель двойного электрического слоя, отвечающая этим простейшим представлениям, приводит к двум возможным значениям -потенциала. Если предположить, что все заряды, находящиеся в растворе, способны перемещаться вместе с жидкостью или при движении твердого тела относительно жидкости не увлекаться вместе с ним, то С-потенциал по своей величине будет совпадать с дьм-потепциалом и его изменение с концентрацией электролита должно подчиняться формуле Нернста. Если же заряды, находящиеся в растворе, при относительном движении жидкости и твердого тела связаны только с последним и перемещаются вместе с ним, то -потенциал всегда будет равен нулю. Ни одно из этих следствий из теории Гельмгольца не согласуется ни с экспериментально установленным соотношением между (или е-) и -потенциалами, ни с опытной зависимостью -потенциала от концентрации. Однако равенство -потенциала нулю может реализоваться в очень концентрированных растворах электролитов или при определенном составе раствора, отвечающем изоэлектрической точке. Теория Гельмгольца не объясняет также изменения заряда поверхности металла при заданном значении е-потенциала, которое наблкадается при введении в раствор поверхностно-активных веществ. Вместе с тем теория конденсированного двойного слоя позволяет получить правильные значения емкости двойного слоя, а при использовании опытных величин емкостей — физически правдоподобную толщину двойного электрического слоя. Для двойного слоя, отвечающего по своим свойствам плоскому конденсатору, можно написать [c.268] По условию электронейтральности удельные поверхностные заряды (или поверхностные плотности зарядов) обеих составляющих частей двойного электрического слоя должны быть равны по абсолютной величине. Условие электронейтральности запишем так ц = —д , где 9+ и — плотности зарядов на обеих обкладках плоского конденсатора, каким по теории Квинке — Гельмгольца представляется двойной электрический слой. Скачок потенциала g в двойном электрическом слое можно рассчитать по известной формуле для плоского конденсатора соответствующая единице площади конденсатора и определяемая по формуле, С = —, где [c.96] chem21.infoЭлектроёмкость конденсатора. Формула конденсатора
Конденсаторы, теория и примеры задач
Определение конденсатора
![Rendered by QuickLaTeX.com \[C=\frac{q}{{\varphi}_1-{\varphi}_2}=\frac{q}{U} \qquad (1), \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-4ec30ecde4dccedc741fa82e62fdae74_l3.png)
 – разность потенциалов между обкладками.
– разность потенциалов между обкладками. Формулы емкости основных типов конденсаторов
 ), который находится между обкладками.
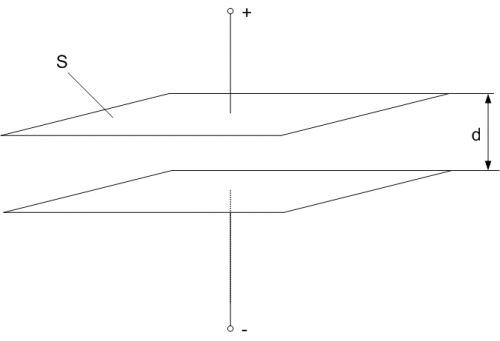
), который находится между обкладками.![Rendered by QuickLaTeX.com \[C=\frac{\varepsilon {\varepsilon}_0S}{d} \qquad (2), \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-47eb03ad4dcc2e2ab29910a945dce3a7_l3.png)
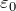 – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
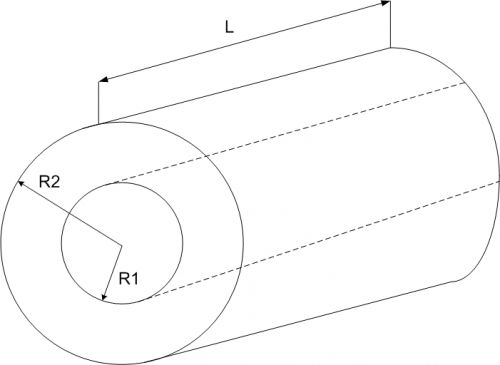
– электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.![Rendered by QuickLaTeX.com \[C=\frac{2\pi \varepsilon {\varepsilon}_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad (3), \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-85e8ec37d8a8d15b12c78f49dad2c86e_l3.png)
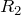 – радиус внешней обкладки;
– радиус внешней обкладки; 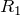 – радиус внутренней обкладки. По формуле (3) вычисляют емкость коаксиального кабеля.
– радиус внутренней обкладки. По формуле (3) вычисляют емкость коаксиального кабеля.![Rendered by QuickLaTeX.com \[C=\frac{4\pi \varepsilon {\varepsilon}_0R_1R_2}{R_2-R_1} \qquad (4), \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0cb607e6743bb5ee07697ecebba2dc67_l3.png)
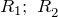 – радиусы обкладок конденсатора. В том случае, если
– радиусы обкладок конденсатора. В том случае, если 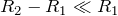 , то можно считать, что
, то можно считать, что 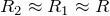 , тогда, мы имеем:
, тогда, мы имеем:![Rendered by QuickLaTeX.com \[C=\frac{4\pi \varepsilon {\varepsilon}_0R^2}{R_2-R_1} \qquad (5), \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bfb4594e374b24f1610d60dd51f83a0f_l3.png)
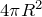 – площадь поверхности сферы, и если обозначить
– площадь поверхности сферы, и если обозначить 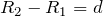 , то получим формулу для емкости плоского конденсатора. При малой величине зазора между обкладками сферического и цилиндрического конденсаторов (в сравнении с их радиусами), можно перейти к расчету емкости при помощи выражения для плоского конденсатора.
, то получим формулу для емкости плоского конденсатора. При малой величине зазора между обкладками сферического и цилиндрического конденсаторов (в сравнении с их радиусами), можно перейти к расчету емкости при помощи выражения для плоского конденсатора. ![Rendered by QuickLaTeX.com \[C=\frac{\pi \varepsilon {\varepsilon}_0l}{ln\left(\frac{d-R}{R}\right)} \qquad (6), \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b1d9a139c2beb81c74a5a784af1cc065_l3.png)
Примеры решения задач
Плоский конденсатор: формулы, особенности, конструкция
Формулы


Из истории
Самый большой в мире плоский конденсатор
Электрофорус
Конструкция плоского конденсатора
Электроёмкость конденсатора: формулы и история
Формулы

История
Термин конденсатор

Электрофорус

Лейденская банка
Идеальный конденсатор
Универсальная формула для нахождения емкости конденсатора
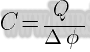 ,
,Как легко найти емкость плоского конденсатора
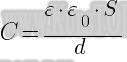 ,
,Емкость провода в оплётке
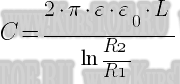 ,
,РАДИОЛЮБИТЕЛЬ, №3, 1925 год. Как рассчитать емкость конденсатора
Как рассчитать емкость конденсатора
Электроемкость
Расчет емкости
Таблица №1
Величины диэлектрической постоянной K
Диэлектрик
К
Воздух
1
Керосин.
2
Шеллак.
2
Каучук
2—2,7
Сера
2—4
Парафин
2,2
Парафиновое масло
Эбонит
2—3
Гуттаперча
2,4
Льняное масло
3,4
Слюда
4—8
Миканит
Стекло
Фарфор
4,5—5
Двойные цифры, напр. 4—8 для стекла, в каких пределах может изменяться диэлектрическая постоянная его, в зависимости от сорта.
C =
K · Sкв. см.
=
K · S
см. ........... (1)
4π · dсм.
12,56 d
примеры
C =
6 × 150
= 239 см. емкости.
12,56 × 0,3
S =
π · d2
=
π · d · d
=
3,14 · 5 · 5
= 19,6 кв. см.
4
4
4
Cбанки =
6 × 176,6
= 423 см.
12,56 × 0,2
C =
2,2 × 162
=
2,2 × 162 × 130
= 3.700 см.
12,56 × 1
C =
K · S1 × (n — 1)
........... (2)
12,56 · d
C =
2,2 × 18 × 9
= 3.700 см.
Гельмгольца формула конденсатора - Справочник химика 21
Теория Гельмгольца принимает, что положительные ионы находятся непосредственно на поверхности твердой фазы, а отрицательные ионы располагаются в слое раствора, прилегающем к этой поверхности на расстоянии 5, приблизительно равном радиусу иона. Образованный таким путем двойной слой можно рассматривать как плоский конденсатор, емкость которого определяется известной формулой (3) [c.206]
Первая теория строения двойного электрического слоя (Гельмгольц) рассматривала его в виде плоского конденсатора, одной обкладкой которого является заряженная поверхность электрода, а вторую образует слой противоположно заряженных ионов, расположенный в электролите. Расстояние между обкладками бц принимается равным радиусу ионов г,.. В таком случае емкость двойног электрического слоя может рассчитываться по формуле [c.101]
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''








Поделиться с друзьями: