В электротехнике часто встречается понятие ёмкости. При этом речь идёт не о ведре или другом сосуде, а об электрической ёмкости проводника, аккумулятора и конденсатора. Путать эти понятия нельзя. В этой статье мы разберемся, что такое электрическая ёмкость, от чего она зависит и в каких единицах измеряется. Для проводников электрической ёмкостью называется величина, которая характеризует способность тела накапливать электрический заряд. Это и есть её физический смысл. Обозначается латинской буквой C. Она равна отношению заряда к потенциалу, если это записать в виде формулы, то получается следующее: C=q/Ф Электроемкость любого предмета зависит от его формы и геометрических размеров. Если рассмотреть проводник в форме шара, в качестве примера, то формула для расчета её величины будет иметь вид: Эта формула справедлива для уединенного проводника. Если расположить рядом два проводника и разделить их диэлектриком, тогда получится конденсатор. Об этом немного позже, сейчас давайте разберемся, в чем измеряется электроемкость. Единица измерения электрической ёмкости — фарад. Если разложить её на составляющие согласно формуле то: 1 фарад =1 Кл/1 В Исторически сложилось так, что размерность этой единицы выбрана не совсем верно. Дело в том, что на практике приходится работать с величинами электроемкости: мили-, микро-, нано- и пикофарад. Что равняется долям фарада, а именно: 1 мФ = 10^(-3) Ф 1 мкФ = 10^(-6) Ф 1 нФ = 10^(-9) Ф 1 пФ = 10^(-12) Ф Конденсатор — это две пластины из проводящего материала, расположенные друг напротив друга, между которым находится слой диэлектрика. В заряженном состоянии обкладки имеют разные потенциалы: одна из них будет положительной, а вторая отрицательной. Электроемкость конденсатора зависит от величины заряда на его обкладках и разности потенциалов, напряжения между ними. Между пластинами возникает электростатическое поле, которое удерживает заряды на обкладках. Формула электрической емкости конденсатора в общем случае: C=q/U Если сказать простыми словами, то емкость конденсатора зависит от площади пластин и расстояния между ними, а также относительной диэлектрической проницаемости материала, расположенного между ними. Их различают по используемому диэлектрику: По форме обкладок: Так как формула площади фигуры зависит от её формы, то и формула ёмкости будет разной для каждого случая. Для плоского конденсатора: Для двух концентрических сфер с общим центром: Для цилиндрического конденсатора: Как и у других элементов электрической цепи и в этом случае есть два основных способа соединения конденсаторов: параллельное и последовательное. От этого зависит итоговая электрическая емкость полученной цепи. Расчёты ёмкости нескольких конденсаторов напоминают расчёты сопротивления резисторов в разном включении, только формулы для способов соединения расположены наоборот, то есть: Cобщ=C1+C2+C3 Cобщ=(1/С1)+ (1/С2)+ (1/С3) Важно! В параллельной схеме соединения напряжения на обкладках каждого элемента одинаковы. Это используют для получения больших значений электроемкости. В последовательном включении двух элементов напряжения на обкладках каждого из конденсаторов составляют по половине общего напряжения. Для трёх – трети и так далее. Основными характеристиками аккумуляторных батарей является: В данном случае для определения количественной характеристики времени работы или, говоря простым языком, чтобы рассчитать, на какое время работы прибора хватит аккумулятора, используют величину ёмкости. В аккумуляторных батареях для описания электрической ёмкости используют следующие размерности: Эти характеристики позволяют определить, сколько времени работы выдержит аккумулятор при конкретной нагрузке. Для определения электрическую емкость аккумулятора измеряют в кулонах (Кл). В свою очередь кулон равен количеству электричества, переданному аккумулятору при силе тока 1А за 1с. Тогда если перевести в часы, то при токе в 1А за 1 час передается 3600 Кл. Одним из способов измерения емкости аккумулятора является его разряд заведомо известным током, при этом вы должны замерить время разряда. Допустим, если аккумулятор разрядился до минимального уровня напряжения за 10 часов током в 5А – значит его емкость 50 А*ч Электроемкость – это важная величина в электронике и электротехнике. На практике конденсаторы применяются практически в каждой схеме электронного устройства. Например, в блоках питания – для сглаживания пульсаций, уменьшения влияния высоковольтных всплесков на силовые ключи. Во времязадающих цепях различных схем, а также в ШИМ-контроллерах для того, чтобы задать рабочую частоту. Аккумуляторы также применяются повсеместно. Вообще задачи накапливания энергии и сдвига фаз встречаются очень часто. Более подробно изучить вопрос поможет предоставленное видео: Кратко объяснение изложено в этом видео уроке: Теперь вы знаете, что такое электрическая емкость, в каких единицах происходит ее измерение и от чего зависит данная величина. Надеемся, предоставленная информация была для вас полезной и понятной! Материалы по теме: samelectrik.ru Ёмкость плоского конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд. Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников. Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин. Под зарядом конденсатора понимают заряд одной пластины. Так же есть: Энергия конденсатора: Ёмкость конденсатора : Ёмкость цилиндрического конденсатора : Емкость сферического конденсатора : В формуле мы использовали : xn--b1agsdjmeuf9e.xn--p1ai Ёмкость цилиндрического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд. Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2 (r2 > r1), один вставлен в другой, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками, так же пренебрегаем краевыми эффектами. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l. При наличии диэлектрика между обкладками разность потенциалов Подставим в формулу электроемкости конденсатора и у нас получится формула для цилиндрического конденсатора: Так же есть: Энергия цилиндрического конденсатора: Ёмкость конденсатора : Ёмкость плоского конденсатора : Емкость сферического конденсатора : В формуле мы использовали : xn--b1agsdjmeuf9e.xn--p1ai Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд. Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так: Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела: При малой величине зазора, то есть Так же есть: Энергия конденсатора: Ёмкость конденсатора : Ёмкость цилиндрического конденсатора : Емкость плоского конденсатора : В Формуле мы использовали : xn--b1agsdjmeuf9e.xn--p1ai Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком. Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками: . Используя определение емкости конденсатора, получаем: Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин. Сферический конденсатор представляет собой систему двух концентрических сфер с радиусамии. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно: . Для ёмкости сферического конденсатора получаем: . Это формула точная. Если , полученная формула переходит в выражение для ёмкости плоского конденсатора. Ёмкость цилиндрического конденсатора. Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной. Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем: .. Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора. Соединение конденсаторов. В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок). Ёмкость последовательного соединения конденсаторов. Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует: или . Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении). Для последовательно соединенных конденсаторов емкость вычисляется по формуле: . В случае одинаковых конденсаторов: . Ёмкость параллельного соединения конденсаторов. Заряд батареи равен сумме зарядов: , а напряжение . По определению емкости получаем: . Для параллельно соединенных конденсаторов:. В случае одинаковых конденсаторов: . Пример. Оценить емкость батареи (см. рисунок). . Ответ:. Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок). Для расчета ёмкости батареи получаем: , . Откуда: , так как, то. Лекция 7. Диэлектрики в электрическом поле. Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния. Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярнымиинеполярными.Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю. Поляризация. В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных» зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично. Под действием электрического поля диполи ориентируются преимущественно в направлении поля. Рассмотрим подробнее этот механизм (см. рисунок). Пара силисоздает вращательный момент равный, где- дипольный момент молекулы. Этот момент стремится ориентировать диполь вдоль поля. В ионных кристаллах под действием электрического поля все положительные ионы смещаются по полю, отрицательные – против поля. Отметим, что смещение зарядов очень малы даже по сравнению с размерами молекул. Это связано с тем, что напряженность внешнего электрического поля обычно много меньше напряженности внутренних электрических полей в молекулах. Отметим, что существуют диэлектрики, поляризованные даже при отсутствии внешнего поля (электреты, сегнетоэлектрики). Мы остановимся на рассмотрении только однородных диэлектриков, в которых отсутствует остаточная поляризация, а объемный и «связанный» заряд всегда равен нулю . studfiles.net При помощи онлайн калькулятора Вы сможете правильно рассчитать объем емкости типа: цилиндра, бочки, цистерны или объем жидкости в любой другой горизонтальной цилиндрической емкости. Определим количество жидкости в неполном баке цилиндрической формы Все параметры указываем в миллиметрах L — Высота бочки. H — Уровень жидкости. D — Диаметр бака. Наша программа в онлайн режиме выполнит расчет количества жидкости в емкости, определит площадь поверхностей, свободную и общую кубатуру. Как посчитать объем бочки Для тог, чтобы правильно рассчитать вместительность резервуара для определения количества жидкости и полезной кубатуры цилиндрической емкости, необходимо определить основные параметры бака. В нашем случае это горизонтальная цистерна. Определение главных параметров кубатуры резервуаров (к примеру, обычная бочка или цистерна) должен производиться, основываясь на геометрическом методе расчета вместительности цилиндров. В отличие от способов калибровки емкости, где подсчет объема выполняют в виде реальных измерений количества жидкости путем мерной линейки (согласно показаниям метрштока). V=S*L – формула расчета объема бака цилиндрической формы, где: L — длина тела. S — площадь поперечного сечения резервуара. Согласно полученным результатам создают калибровочные таблицы емкости, которые еще называются тарировочными, позволяют определить вес жидкости в баке по удельному весу и объему. Эти параметры будут зависеть от уровня наполнения цистерны, который можно измерять при помощи метрштока. Наш онлайн калькулятор предоставляет возможность выполнить расчет вместительности горизонтальных и вертикальных емкостей по геометрической формуле. Вы сможете узнать полезную вместительность резервуара более точно, если при этом правильно определите все главные параметры, которые указаны выше и участвуют в расчете. Как правильно определить основные данные Определяем длину L При помощи обычной рулетки, Вы сможете измерить длину L цилиндрического резервуара с неплоским дном. Для этого Вам необходимо замерить расстояние между пересекающими линиями днища с цилиндрическим телом емкости. В случае, когда горизонтальный бак с плоским дном, то для того, чтобы определить размер L, достаточно измерить длину резервуара по наружной стороне (от одного края бака до другого), и от полученного результата вычесть толщину дна. Определяем диаметр D Проще всего определить диаметр D бочки цилиндрической формы. Для этого достаточно при помощи рулетки замерять расстояние между двумя любыми крайними точками крышки или края. Если трудно правильно выполнить расчет диаметра емкости, то в этом случае можно использовать измерение длины окружности. Для этого при помощи обычной рулетки обхватываем по окружности весь резервуар. Для правильно расчета окружности делают два измерения в каждом сечении резервуара. Для этого поверхность, измеряемая должна быть чистой. Узнав усредненную длину окружности нашей емкости – Lокр, переходим к определению диаметра по следующей формуле: d=Lокр/3,14 Этот метод наиболее простой, так как зачастую измерение диаметра бака сопровождается рядом затруднений, связанных с нагромождением на поверхности различного вида оборудования. Важно! Измерения диаметра правильней всего выполнить в трех разных сечениях емкости, и после этого выполнить подсчет среднего значения. Так как зачастую, эти данные могут существенно отличаться. Усредненные значения после трех замеров позволяют минимизировать погрешность расчета объема резервуара цилиндрической формы. Как правило, используемые накопительные баки во время эксплуатации подвергаются деформации, могут терять прочность, уменьшаться в размерах, что ведет к уменьшению количества жидкости внутри. Определяем уровень H Чтобы определить уровень жидкости, в нашем случае это H, нам понадобиться метршток. При помощи этого измерительного элемента, который опускают на дно емкости, мы сможем точно определить параметр H. Но эти расчеты будут верны для резервуаров с плоским дном. В результате подсчета онлайн калькулятора мы получаем: o-builder.ru
Не знаю как Вам, а мне никогда не нравилось работать и вычислять ёмкости конденсаторов. Больше всего раздражало наличие в исходных данных, ёмкостей в разных номиналах, в пикофарадах, в нанофарадах, микрофарадах. Их приходилось переводить в Фарады, что влекло за собой глупейшие ошибки в расчетах.
Конденсатор - в принципе это любая конструкция, которая может сохранять накопленный электрический потенциал. Если же эта конструкция, не только хранит электроэнергию, но и генерирует её, то это уже источник электропитания и никак не конденсатор.
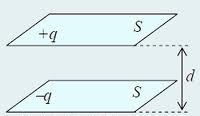
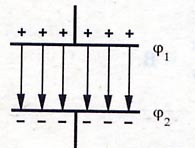
Конструкция конденсаторов может быть любой, но чаще всего в практике используется плоский конденсатор, состоящий из двух проводящих пластин, между которыми находится какой либо диэлектрик. Это связано с тем, что расчет ёмкости такого конденсатора ведется по известной формуле и простотой его создания. Свернув такой плоский конденсатор в рулон, мы получаем, что при фактическом скромном размере "рулона", там находится плоский конденсатор, длиной в десятки сантиметров и обладающий повышенной ёмкостью.
Емкости конденсаторов некоторых форм известны, и мы дальше их рассмотрим.
Но хотелось бы заметить, что на наш взгляд, потенциал развития конденсаторов до конца не завершен. Ведь форма конструкции какого либо конденсатора может быть любая, материалы из которого сделаны обкладки или диэлектрический слой тоже могут быть любыми в пределах таблицы Менделеева. Единственная сложность, это невозможность теоретически просчитать потенциальную ёмкость, новосозданного (другой конструкции) конденсатора. Это усложняет нахождение самой лучшей конструкции конденсатора.
Есть хорошая книга по рассмотрению электрической ёмкости различных фигур. Для любопытных рекомендую поискать на просторах Интернета: Расчет электрической ёмкости в авторстве Ю.Я.Иоселль 1981 года
Данный бот рассчитывает параметры типовых форм конденсаторов. Отличие от других калькуляторов, присутствующих в интернете, это возможность задавать параметры, которые Вам известны, для того что бы рассчитать остальные.
И последнее нововведение, которое вы можете использовать. Вам не обязательно придется переводить заданные данные в метры, фарады и т.д. Достаточно обозначить размерность данных.
Например, если ёмкость известна и равно 100 пикофарад, то боту можно так и написать c=100пикофарад или с=100пФ, бот сам переведет в Фарады.
Результат, тоже будет выдан оптимально визуальному восприятию пользователя.
Это стало возможно с созданием бота Система единиц измерения онлайн
Ёмкость такого сооружения определяется следующей формулой.
где ε0 = 8,85.10-12 Ф/м - абсолютная диэлектрическая проницаемость
Если же конденсатор состоит не из пары пластин, а каого то n-ого количества плоских пластин то ёмкость такого "слоёного" конденсатора составит
Еще интереснее выглядит формуа такого "слоёного" конденсатора, если в слоях находятся разные диэлектрики , разной толщины d
S- площадь одной из обкладок конденсатора ( предполагаем что другая обкладка имеет такую же площадь)
d- расстояние между обкладками
С- ёмкость конденсатора
Рассмотрим примеры
Задача: Ёмкость плоского конденсатора 350 нанофарад, расстояние между обкладками 1 миллиметр, и заполнено воздухом. Определить какова площадь обкладок?
Сообщаем боту что нам известно: C=350нФ, d=1мм. Так как у воздуха диэлектрическая проницаемость 1.00059 то e=1.00059. Поле площадь очистим, так именно его мы будем определять
Получаем вот такой ответ
d = 1 милиметр
e = 1.00059
C = 350 нанофарад
S = 39.524703024086 м2
Ответ, площадь обкладок конденсатора при таких значениях должна составлять почти 40 квадратных метров.
Цилиндрический конденсатор представляет в простейшем случае две трубки разного диаметра вложенных друг в друга. разделенных диэлетриком
Иногда может получится так, что ёмкость цилиндрического конденсатора станет отрицательной величиной. Ничего страшного, это лишь говорит о том что Вы перепутали радиусы внешней и внутренней оболочки местами. www.abakbot.ruЧто такое электрическая емкость и в чем она измеряется. Формула емкости
Электрическая емкость: определение, формулы, единицы измерения
Определение



Конденсаторы



Аккумуляторы и электроемкость
Ёмкость плоского конденсатора | Все формулы
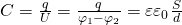

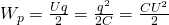
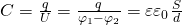

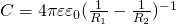
 — Электрическая ёмкость (ёмкость конденсатора)
— Электрическая ёмкость (ёмкость конденсатора) — Относительная диэлектрическая проницаемость
— Относительная диэлектрическая проницаемость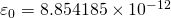 — Электрическая постоянная
— Электрическая постоянная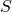 — Площадь одной обкладки
— Площадь одной обкладки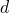 — Расстояние между обкладками
— Расстояние между обкладками — Напряжение на обкладках
— Напряжение на обкладках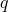 — Заряд конденсатора
— Заряд конденсатораЁмкость цилиндрического конденсатора | Все формулы

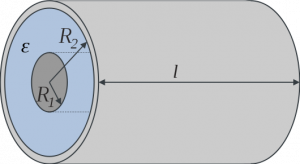
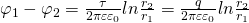

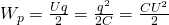
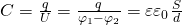
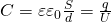
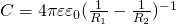
 — Ёмкость цилиндрического конденсатора
— Ёмкость цилиндрического конденсатора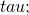 — Линейная плотность
— Линейная плотность — Относительная диэлектрическая проницаемость
— Относительная диэлектрическая проницаемость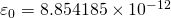 — Электрическая постоянная
— Электрическая постоянная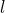 — Длина цилиндрического конденсатора
— Длина цилиндрического конденсатора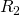 — Больший радиус (от центра, до края конденсатора)
— Больший радиус (от центра, до края конденсатора)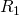 — Малый радиус (Его может и не быть — это пустота)
— Малый радиус (Его может и не быть — это пустота)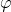 — Потенциал проводника
— Потенциал проводника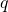 — Точечный заряд
— Точечный заряд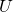 — Напряжение
— НапряжениеЁмкость сферического конденсатора | Все формулы
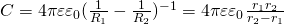


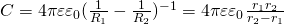
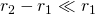 , а следовательно можно считать, что
, а следовательно можно считать, что 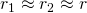 емкость сферического конденсатора будет равна
емкость сферического конденсатора будет равна  . Площадь сферы
. Площадь сферы 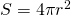 следовательно формула будет совпадать с формулой емкости плоского конденсатора
следовательно формула будет совпадать с формулой емкости плоского конденсатора 
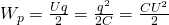
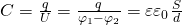

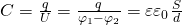 ;
; — Электроемкость сферического конденсатора
— Электроемкость сферического конденсатора — Относительная диэлектрическая проницаемость
— Относительная диэлектрическая проницаемость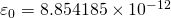 — Электрическая постоянная
— Электрическая постоянная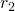 — Больший радиус (от центра, до края конденсатора)
— Больший радиус (от центра, до края конденсатора)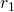 — Малый радиус (Его может и не быть — это пустота)
— Малый радиус (Его может и не быть — это пустота)Ёмкость плоского конденсатора.
Ёмкость сферического конденсатора.
Калькулятор расчета жидкости в бочке, цистерне, цилиндре
Инструкция для калькулятора расчета физических показателей круглой емкости

Расчет параметров конденсатора онлайн
Расчет параметров конденсатора онлайн
Плоский конденсатор. Параметры
Самая простая и самая распространенная конструкция конденсатора это два плоских проводника разделенных тонким слоем диэлектрика ( то есть материала не проводящего электрический ток). Полученные характеристики плоского конденсатора
Полученные характеристики плоского конденсатора
Цилиндрический КОНДЕНСАТОР
Полученные характеристики цилиндрического конденсатора
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: