Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами. В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость. Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения где ω – количество витков катушки, RM – сопротивление магнитной цепи, μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник, SM – площадь поперечного сечения сердечника, lM – длина средней магнитной силовой линии, Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %. Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле где ω – количество витков катушки, μ0 – магнитная постоянная, μ0 = 4π*10-7, μr – относительная магнитная проницаемость вещества, Se – эффективная площадь поперечного сечения сердечника, le – эффективный путь магнитной линии сердечника. Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников: С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1; С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3; где N – количество разнородных участков сердечника, lN – длина N – го участка сердечника, SN – площадь N – го участка сердечника. Тогда величины Se и le определятся из следующих выражений Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению где ω – количество витков катушки, μ0 – магнитная постоянная, μ0 = 4π*10-7, μr – относительная магнитная проницаемость вещества, С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника. Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое. Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них. Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях. Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника. Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют где he – эффективная высота сердечника, D1 – внешний диаметр сердечника, D2 – внутренний диаметр сердечника. Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей. Рассмотрим несколько случаев: а) прямоугольное поперечное сечение с острыми кромками б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs в) трапецеидальное поперечное сечение с острыми кромками г) трапецеидальное поперечное сечение со скруглёнными кромками Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000. Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины. Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность. Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника Неизвестные величины можно найти следующим образом Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150. Таким образом, расчётные параметры сердечника составят Таким образом коэффициент С1 и индуктивность L составят Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок. Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60. Параметры сердечника для расчёта составят Таким образом коэффициент С1 и индуктивность L составят На сегодня всё. Продолжение смотри в следующей статье. Теория это хорошо, но теория без практики - это просто сотрясание воздуха. Перейдя по ссылке всё это можно сделать своими руками Скажи спасибо автору нажми на кнопку социальной сети www.electronicsblog.ru Для того, чтобы поделиться созданным вами проектом, нужно скопировать ссылку и вставить её в блог, форум или другой сайт: Калькулятор позволяет найти оптимальную зависимость параметрического изменения индуктивности от тока, и рабочий режим возбуждающего генератора, для получения максимального КПД в замкнутой RL-цепи, где в качестве источника энергии выступает обратная ЭДС. L = LS‧M(I), где: M(I) = (1 + k11‧I + k12‧I2 + k13‧I3 + k14‧I4 )/(1 + k21‧I + k22‧I2 + k23‧I3 + k24‧I4) Все значения в данном калькуляторе — относительные. Для вычисления реальных значений необходимо знать намоточные данные катушки и параметры сердечника. gorchilin.com Расчет катушки индуктивности Расчет однослойной воздушной катушки индуктивности Расчет дросселя без сердечника Расчетная формула: Индуктивность в мкГн = R2 * N2 / ( 25.4*R + 22.9*L ) R = радиус катушки по центру провода (см) N = количество витков в катушке (может быть не целым числом) L = длина катушки (см) - возможна намотка не виток к витку, а с зазором. результат конечно приблизителен! Реклама недорогих радиодеталей почтой: А вот результаты измерения реальных катушек с помощью измерителя импеданса: Hewlett Packard 4192A LF Impedance Analyzer Вы можете проверить по этим таблицам результат расчета. Все катушки мотались медным эмалевым обмоточным проводом 0.6 мм. Максимальная добротность достигается при намотке с зазором между витками равными диаметру провода! Таблица для катушек: Радиус 0.36 см провод 0.6 мм Таблица для катушек: Радиус 0.29 см провод 0.6 мм proavr.narod.ru Рисунок 1 - Катушка Индуктивность - это коэффициент связывающий ток (силу тока) I протекающий по виткам катушки и её потокосцепление, математически это можно представить в виде формулы (1): Из (1) можно выразить индуктивность: В знаменателе формулы (3) длинна l.Подставим (3) в (2) и получим формулу для расчёта индуктивности, для данного случая: Так как сечение круглое и известен диаметр d то площадь можно найти по формуле: Диаметр берется средний.Подставим найденную площадь S; известные: число витков w, длину l, магнитную проницаемость материала сердечника, магнитную проницаемость вакуума в (4) и найдем индуктивность для нашего примера (рисунок 1): Если число слоёв катушки не велико (несколько слоёв) а диаметр провода мал по отношению к её размерам то можно воспользоваться формулой (4) и получить приближенный результат. Необходимо учитывать что форма катушки может быть такой что результат расчёта её индуктивности по формуле (4) может быть очень неточным. electe.blogspot.comЭлектротехника. Расчет катушки индуктивности без сердечника онлайн
Как рассчитать индуктивность катушек с замкнутыми сердечниками?
Особенности расчёта индуктивных элементов с сердечниками
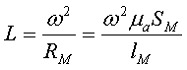
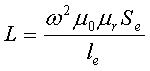
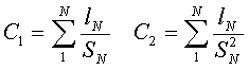

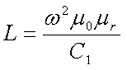
Расчёт катушки с тороидальным сердечником
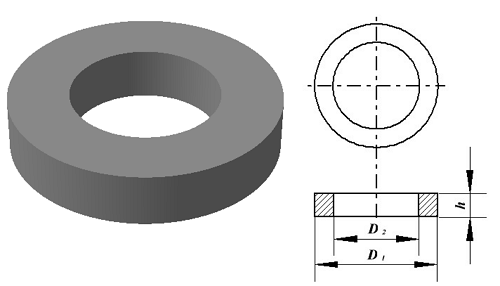 Тороидальный сердечник.
Тороидальный сердечник. 
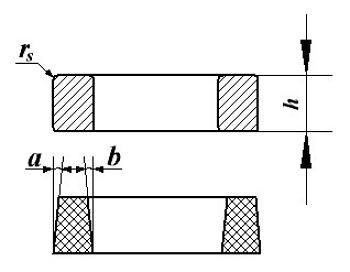 Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу). 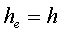


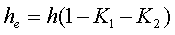
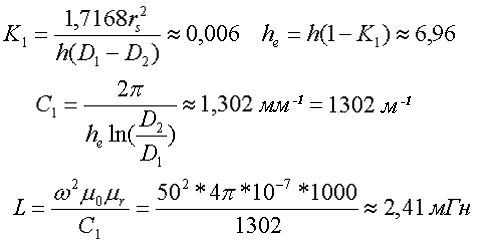
Расчёт катушки с П–образным сердечником прямоугольного сечения
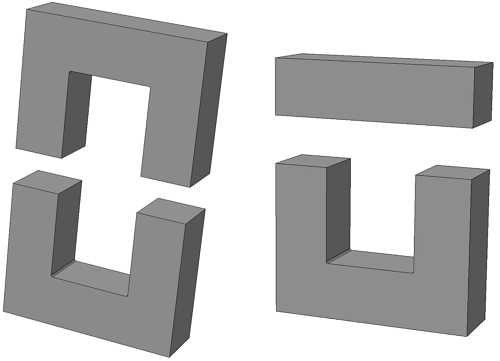 П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа). 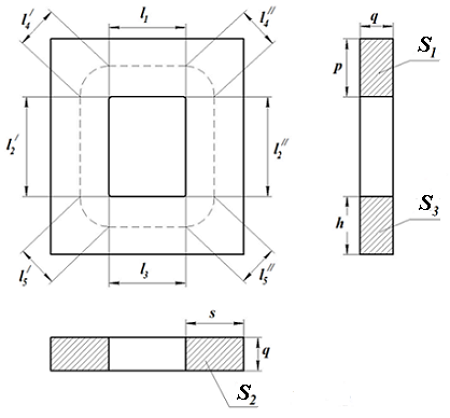 Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
Сечение П-образного прямоугольного сердечника. Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят 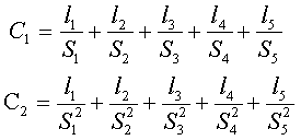
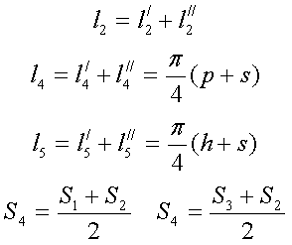
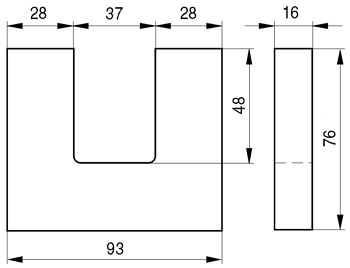 Сердечник Epcos U93/76/16.
Сердечник Epcos U93/76/16.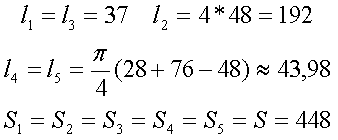

Расчёт катушки с П-образным сердечником круглого сечения
 П-образный сердечник с круговым сечением.
П-образный сердечник с круговым сечением.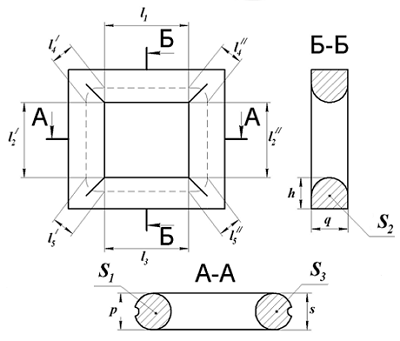 Сечение П-образного сердечника с круговым сечением.
Сечение П-образного сердечника с круговым сечением.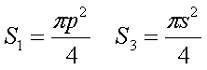
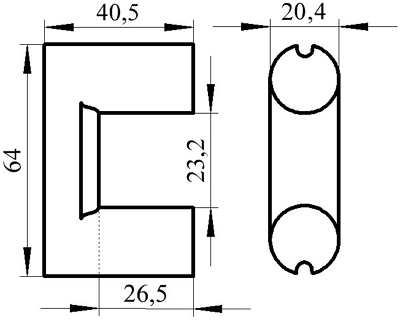 Сердечник типа SDMR 40 UY20.
Сердечник типа SDMR 40 UY20.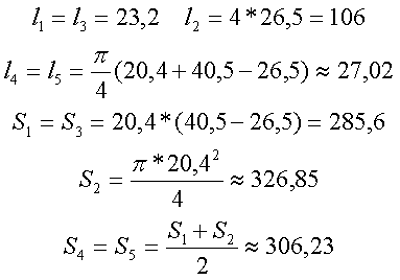
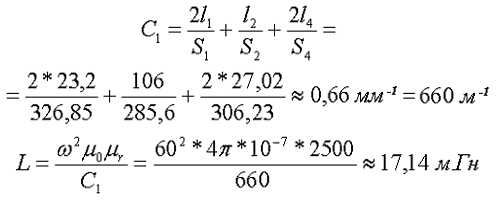
Свободная энергия обратной ЭДС в катушке индуктивности с сердечником. Онлайн калькулятор
Inductance Calculator
Сайт управляется системой uCoz Витков нГн(плотная намотка) Q-добротность на 13 МГц(плотная намотка) нГн(намотка с зазорами) Q-добротность на 13 МГц(намотка с зазорами) 3 77 407 66 440 4 122 325 102 560 5 177 340 - - 6 240 440 206 550 7 306 509 290 690 8 379 607 319 1300 9 470 1500 422 >1500 10 582 >1000 515 >1000 11 644 >1000 - >1000 12 656 >1000 545 >1000 13 745 >1000 612 >1000 14 789 >1000 658 >1000 Витков нГн(плотная намотка) Q-добротность на 13 МГц(плотная намотка) нГн(намотка с зазорами) Q-добротность на 13 МГц(намотка с зазорами) 4 92 540 79 - 5 131 370 120 530 6 175 340 155 500 7 220 300 184 640 8 272 370 234 560 9 315 470 267 770 10 363 650 313 1270 Электротехника: Расчёт индуктивности однослойной катушки.
На рисунке 1 представлена однослойная катушка: имеющая круглое сечение, не имеющая сердечника (магнитная проницаемость равна единице), длинной l=0.01м, диаметром d=0.01м, числом витков w=3:
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: