Потенциал уединенного проводника пропорционален сообщенному ему заряду, поэтому отношение заряда проводника к его потенциалу не зависит от заряда и является характеристикой данного проводника. Электроемкостью уединенного проводника называют величину, равную отношению заряда проводника к потенциалу этого проводника. . На практике применяются Электроемкость проводника не зависит от вещества, из которого он изготовлен, а зависит от его формы, размеров и диэлектрической проницаемости среды, в которой находится этот проводник. Используя формулу потенциала электрического поля, созданного равномерно заряженным шаром , для емкости шара получим . КОНДЕНСАТОРЫ Уединенные проводники обладают малой емкостью. На практике возникает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе значительные заряды. Конденсатором называют систему, состоящую из двух разделенных диэлектриком проводников, на которых могут накапливаться заряды противоположных знаков. Проводники, образующие конденсатор, называют обкладками. Чтобы внешние тела не влияли на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две близко расположенные пластины, два коаксиальных цилиндра и две концентрические сферы. Емкостью конденсатора называют величину, равную отношению заряда конденсатора к разности потенциалов (напряжению) между его обкладками =. ЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА Напряженность поля между обкладками плоского конденсатора . Для однородного поля справедливо соотношение . Следовательно, емкость плоского конденсатора (S – площадь обкладок, d – расстояние между обкладками). При параллельном соединении конденсаторов напряжения на каждом конденсаторе одинаковы и равны напряжению на клеммах батареи . Заряд батареи . Исходя из того, что , имеем , поэтому . При последовательном соединении конденсаторов , . Учитывая, что , имеем , поэтому при последовательном соединении конденсаторов . ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА При зарядке конденсатора совершается работа по перемещению электрических зарядов против сил электрического поля. При перемещении заряда совершается работа. Учитывая, что, получим. Следовательно, . По закону сохранения энергии эта работа равна энергии заряженного конденсатора, т.е. . Используя формулы и, получим и . Участок цепи, на котором не действуют сторонние силы, приводящие к возникновению ЭДС, называется однородным. Согласно закону Ома для однородного участка цепи постоянного тока: сила тока в однородном проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению данного проводника. . Опыты показывают, что сопротивление R проводника пропорционально его длине, обратно пропорционально площади его поперечного сечения и зависит от вещества, из которого изготовлен проводник. Для однородного проводника длиной l и неизменной площадью поперечного сечения S эту зависимость выражают формулой , где - коэффициент пропорциональности, называемый удельным электрическим сопротивлением. Удельное сопротивление равно сопротивлению проводника, изготовленного из данного вещества и имеющего единичную длину и единичную площадь поперечного сечения. Удельное сопротивление есть свойство проводника и зависит от его состояния. Сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений этих проводников. . Сопротивление цепи, состоящей из параллельно соединенных проводников можно определить из формулы studfiles.net Будем рассматривать уединенный проводник, т. е. проводник, значительно удаленный от других проводников, тел и зарядов. Его потенциал, как известно, прямо пропорционален заряду проводника. Из опыта известно, что разные проводники, будучи при этом одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать Величину (1) называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость уединенного проводника зависит от его размеров и формы, но не зависит от материала, формы и размеров полостей внутри проводника, а также его агрегатного состояния. Причиной этому есть то, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит ни от заряда проводника, ни от его потенциала. Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, у которого потенциал изменяется на 1 В при сообщении ему заряда 1 Кл. Согласно формуле потенциала точечного заряда, потенциал уединенного шара радиуса R, который находится в однородной среде с диэлектрической проницаемостью ε, равен Применяя формулу (1), получим, что емкость шара (2) Из этого следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус R=C/(4πε0)≈9•106 км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С≈0,7 мФ). Следовательно, фарад — довольно большая величина, поэтому на практике применяются дольные единицы - миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (2) следует также, что единица электрической постоянной ε0 — фарад на метр (Ф/м) (см. (78.3)). Как нам известно из формулы емкости уединенного проводника, для того чтобы проводник имел большую емкость, он должен иметь довольно большие размеры. На практике необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать большие по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов. Если к заряженному проводнику перемещать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, при этом наиболее близкими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, очевидно, ослабляют поле, которое создается зарядом Q, т. е. уменьшают потенциал проводника, что приводит, следуя из формулы зависимости емкости от потенциала С=Q/φ к повышению его электроемкости. Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создавается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические. Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостьюконденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками: (1) Найдем емкость плоского конденсатора, который состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если считать, что расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами на пластинах можно пренебречь и поле между обкладками считать однородным. Его можно найти используя формулу потенциала поля двух бесконечных параллельных разноименно заряженных плоскостей φ1-φ2=σd/ε0. Учитывая наличие диэлектрика между обкладками: (2) где ε — диэлектрическая проницаемость. Тогда из формулы (1), заменяя Q=σS, с учетом (2) найдем выражение для емкости плоского конденсатора: (3) Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r1 и r2(r2 > r1), один вставлен в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов (4) Подставив (4) в (1), найдем выражение для емкости цилиндрического конденсатора: (5) Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов (6) Подставив (6) в (1), получим Если d=r2—r1<<r1, то r2≈r1≈r и C=4πε0εr2/d. Так как 4πr2 — есть площадь сферической обкладки, то мы снова получим формулу (3). Значит, при малой величине зазора между обкладками конденсатора по сравнению с радиусом сферы выражения для емкости плоского и сферического конденсаторов совпадают. Этот вывод справедлив и для цилиндрического конденсатора: при малом зазоре между его цилиндрическими обкладками по сравнению с их радиусами в формуле (5) ln (r2/r1) можно разложить в ряд, делая приближение только членом первого порядка. В результате опять приходим к формуле (3). Из формул (3), (5) и (7) следует, что емкость конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости диэлектрика, который заполняет пространство между обкладками. Поэтому применение сегнетоэлектриков в качестве прослойки значительно увеличивает емкость конденсаторов. Конденсаторы также характеризуются пробивным напряжением — разностью потенциалов между обкладками конденсатора, при которой происходит пробой — электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение также зависит от формы обкладок, свойств диэлектрика и его толщины. Для увеличения емкости и изменения ее возможных значений конденсаторы соединяют в батареи, при этом применяется их параллельное и последовательное соединения. 1. Параллельное соединение конденсаторов (рис. 1). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна φA – φB. Если емкости отдельных конденсаторов С1, С2, ..., Сn, то, как видно из (1), их заряды есть .............. а заряд батареи конденсаторов Полная емкость батареи т. е. при параллельном соединении конденсаторов полная емкость равна сумме емкостей отдельных конденсаторов. Рис.1 2. Последовательное соединение конденсаторов (рис. 2). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи где для любого из рассматриваемых конденсаторов Δφi = Q/Сi. С другой стороны, откуда т. е. при последовательном соединении конденсаторов суммируются величины, которые обратны емкостям. Значит, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, которая используется в батарее. studfiles.net Электроемкость конденсатора - это его способность накапливать электрический заряд. Формула электроемкости следующая. C=q/U Измеряется эта величина в фарадах. Как правило, емкость элемента очень мала и измеряется в пикофарадах. В задачах часто спрашивается, как изменится электроемкость конденсатора, если увеличить заряд или напряжение. Это вопрос с подвохом. Проведем другую аналогию. Представьте, что речь идет про обычную банку, а не конденсатор. Например, у вас она трехлитровая. Аналогичный вопрос: что произойдет со вместимостью банки, если туда налить 4 литра воды? Разумеется, вода просто выльется, но при этом размеры банки никак не изменятся. То же самое с конденсаторами. Заряд и напряжение никак не влияют на емкость. Этот параметр зависит только от реальных физических размеров. Формула будет следующей Только эти параметры влияют на реальную электроемкость конденсатора. На любом конденсаторе есть маркировка с техническими параметрами. Разобраться несложно. Достаточно минимальных знаний по электричеству. Конденсаторы, так же как и сопротивления, можно подключать последовательно и параллельно. Кроме этого, в схемах бывают и смешанные соединения. Как видите, электроемкость конденсатора в обоих случаях считается по-разному. Это также относится к напряжению и заряду. По формулам видно, что электроемкость конденсатора, вернее, их совокупности в схеме, будет наибольшей при параллельном соединении. При последовательном общая емкость значительно уменьшается. При подключении последовательно заряд размещается равномерно. Он будет везде одинаков - как суммарный, так и на каждом конденсаторе. А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач. Напряжение считается наоборот. При последовательном соединении складываем, а при параллельном оно равно везде. Здесь приходится выбирать: если вам нужно больше напряжения, тогда жертвуем емкостью. Если емкость, то огромного напряжения не будет. Существует огромное количество конденсаторов. Они отличаются как по размеру, так и по форме. Разумеется, емкость вычисляется у всех по-разному. Электроемкость плоского конденсатора определяется проще всего. Эту формулу в основном все и помнят, в отличии от других. Здесь всё зависит от физических параметров и среды между пластинами. Здесь также большое значение имеет, какой диэлектрик или материал помещен внутрь. Так как деталь имеет размер сферы, ее емкость зависит от радиуса. В случае с цилиндрической формой, кроме среды внутри, значение имеют радиусы и длина цилиндра. Подумайте, как изменится электроемкость плоского конденсатора, если на нем будут повреждения? Существуют различные сбои, которые могут повлиять на работоспособность конденсаторов. Например, они рассыхаются или вздуваются. После этого они становятся непригодными для нормальной работы устройства, куда установлены. Рассмотрим примеры повреждений и выхода из строя конденсаторов. Вздуться могут все сразу. Иногда из строя выходят только несколько. Такое бывает, когда конденсаторы разных параметров или качества. Наглядный пример порчи (вздутие, разрыв и выход наружу содержимого). Если вы увидите вот такие ленты, это крайняя степень повреждения. Хуже и быть не может. Если вы заметите на устройстве (например на видеокарте в компьютере) такие вздутые конденсаторы, это повод задуматься о замене детали. Подобные проблемы можно устранить только заменой на аналогичную деталь. У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной. Менять конденсаторы нужно аккуратно, не повредив платы. Выпаивать нужно быстро, не допуская перегрева. Если вы не умеете этого делать, лучше отнесите деталь в ремонт. Основной причиной разрушения является перегрев, который возникает в случае старения или большого сопротивления в цепи. Рекомендуется не затягивать с ремонтом. Поскольку у поврежденных конденсаторов изменяется емкость, устройство, где они расположены, будет работать с отклонением от нормы. И со временем это может стать причиной выхода из строя. Если у вас на видеокарте вздулись конденсаторы, то их своевременная замена может исправить ситуацию. В противном случае может сгореть микросхема или что-то еще. В таком случае ремонт будет стоить очень дорого или вовсе окажется невозможным. Выше был приведен пример с банкой воды. Там говорилось, что если воды налить больше, то воды выльется. А теперь подумайте, куда могут "вылиться" электроны в конденсаторе? Ведь он запечатан полностью! Если вы подадите в цепи больше тока, чем тот, на который рассчитан конденсатор, то как только он зарядится, его излишек попытается выйти куда-то. А пространства свободного нет. Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет. Будьте аккуратны! www.syl.ru Так как у проводника ϕ = const , тоE перпендикулярен поверхно- сти проводника (силовые линии ортогональны эквипотенциальной поверхности проводника). Применим теорему Гаусса для любого объема внутри проводника: S∫En dS= ε 1ε0 V∫ρ dV= 0 . Отсюда следует, что ρ = 0 внутри проводника в равновесии. Таким образом, индуцированный или избыточный заряд в равновесии может находиться только на поверхности проводника. На рис. 43 показаны силовые линии электростатического поля при помещении в него проводника. + − Можно показать, что между зарядом − + проводника Q и его потенциаломϕ сущест- вует прямо пропорциональная зависимость: − + − + Q = Cϕ, гдеC– коэффициент пропорцио- − + − + − + + нальности, который называется электроем- − − костью уединенного проводника. Таким об- разом, величина C численно равна заряду, Рис. 43 который необходимо сообщить проводнику, чтобы его потенциал стал равен 1 В. Конденсатор – система двух разноименно заряженных равными по абсолютной величине зарядами проводников, таких, что поле, создаваемое ими, сосредоточено между ними. Эти проводники называют обкладками конденсатора. Рассмотрим систему, состоящую из двух параллельных разноименно заряженных пластин, расстояние между которыми d много меньше линейных размеров пластин (рис. 44). Такой конденсатор называется плоским конденсатором. Заряды на пластинах удовлетворяют условию Q1 = −Q2 , Q1 =Q2 =Q. Разность потенциалов между двумя произвольными точками на одной и другой пластинах выражается формулой 2' σ 2 σ Qd ϕ1 −ϕ2 =∫El dl =∫ dl + ∫0dl= d = . εε0 εε0 Sεε0 l 1 2' Следовательно, заряд конденсатора пропорционален разности потенциалов между обкладками конденсатора: Q = Ck (ϕ1 − ϕ2 ). studfiles.net Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная: называется емкостью конденсатора. Где q – величина заряда одной из обкладок конденсатора, а Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в где Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф). Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как: где Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как: где l – высота цилиндров; Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как: где ru.solverbook.com Любой уединенный проводник может накапливать заряд qпропорционально своему потенциалу φ:. С – это электроемкость проводника, численно равная величине заряда q, вызвавшей увеличение потенциала проводника φ на единицу. Единица измерения в СИ: . Электроемкость уединенного проводника изменяется в присутствии других проводников и диэлектриков. Устройства для накопления электрического заряда, неподверженное влиянию внешних тел, называют конденсаторами. Конденсатор представляет собой два проводника (обкладки), разделенных диэлектриком, на которых могут накапливаться заряда разных знаков. Электроемкость конденсатора определяется по формуле: и зависит только от параметров самого конденсатора – его формы, геометрических размеров и диэлектрической проницаемостидиэлектрика, находящегося между обкладками. Электроемкость плоского конденсатора:, где 0- электрическая постоянная вакуума,S- это площадь обкладок конденсатора,d- расстояние между обкладками. Электроемкость шарового конденсатора радиуса R: . Электроемкость сферического конденсатора: , где R1,R2– радиусы внутренней и внешней обкладок. Электроемкость цилиндрического конденсатора длиной l: , где R1,R2– радиусы внутренней и внешней обкладок. При последовательном соединении конденсаторов (рис.3.3, а) заряд системы , разность потенциалов, а общая емкость системы конденсаторов равна:. При параллельном соединении конденсаторов (рис.3.3, б) заряд системы , разность потенциалов, а общая емкость системы конденсаторов равна:. Конденсатор накапливает между своими обкладками электрическую энергию , которая выделяется в проводнике при разрядке конденсатора. Плотность энергии электрического поля напряженностью , созданного в среде с проницаемостью, равна:. Электрический ток – это упорядоченное движение заряженных частиц. За направление тока принимают направление движения положительно заряженных частиц (от «+» к «-»). Количественной характеристикой является сила тока I– это заряд, переносимый через рассматриваемую поверхность в единицу времени . Единица измерения в СИ: . Плотностью тока называется вектор , совпадающий с направлением электрического тока и численно равный отношению силы токаdIчерез малый элемент поверхности, расположенной нормально направлению тока, к площадиdSnэтого элемента:. Если направление и сила тока не меняются с течением времени, то ток называется постоянным. Для постоянного тока справедливо соотношение: . Кулоновские силы взаимодействия между зарядами неспособны поддерживать ток в замкнутой цепи. Для этого необходимо наличие сил неэлектростатического происхождения (сторонние силы), которые поддерживают на концах проводника постоянную разность потенциалов, совершая работу над движущимися по цепи зарядами. Физическая величина, равная работе сторонних сил Астнад единичным положительным зарядомq, называется электродвижущая сила (ЭДС):. Единица измерения ЭДС с СИ:. Величина, численно равная работе электростатических и сторонних сил, совершаемой при перемещении единичного положительного заряда на участке цепи 1-2, называется напряжением U1,2на этом участке цепи (): . Участок цепи, на котором не действуют сторонние силы, называется однородным. Для него был установлен закон (закон Ома): сила тока, текущего по однородному металлическому проводнику, пропорциональна напряжению U: , где , аR- сопротивление участка. Величина сопротивления проводника зависит от свойств металла, формы и размеров проводника , где l- длина проводника,S– площадь поперечного сечения, ρ – удельное электрическое сопротивление. Единица измерения в СИ:. Зависимость удельного сопротивления проводников от температуры: , где ρ и ρ0– удельные сопротивления при температуреt и 0ºС,- температурный коэффициент сопротивления. Закон Ома для неоднородного участка цепи (на котором действуют сторонние силы): . Если цепь замкнута, то φ1=φ2, и. При наличии в цепи нескольких проводников с разным сопротивлением R, общее сопротивление цепи рассчитывается с учетом их взаимного расположения. При последовательном соединении проводников (рис.3.4, а) сила тока во всех проводниках одинакова , разность потенциалов, а общее сопротивление:. При параллельном соединении проводников (рис. 3.4, б) сила тока в цепи будет находиться как сумма всех токов , разность потенциалов на каждом проводнике будет одинакова, а общее сопротивление: . Работа, совершаемая силами электростатического поля и сторонними силами по перемещению заряда в проводнике, находится как: . Мощность тока: . Мощность, выделяемая на однородном участке цепи: . Ток короткого замыкания:. Коэффициент полезного действия источника с сопротивлением r: . Количество теплоты, выделяемое в проводнике при прохождении через него электрического тока, определяется по закону Джоуля - Ленца: . studfiles.net Видеоурок 2: Емкость плоского конденсатора. Классификация конденсаторов Лекция: Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора Для определения понятия конденсатора, необходимо воспользоваться всеми знаниями по поводу проводников и диэлектриков, поскольку и те, и другие одновременно используются для изготовления конденсаторов. Во время изучения понятия конденсаторов будем использовать термин "уединенный конденсатор". Он значит, что данное проводящее тело находится вне поля действия других тел. Рассмотрим проводник, у которого имеется какой-то определенный потенциал "фи". Данный потенциал является пропорциональным к величине заряда проводника. Данный коэффициент принято обозначать 1/С. В данном случае величина, что находится в знаменателе, является электрической ёмкостью имеющегося проводника. Если рассматривать некоторый объемный шар в виде проводника, то его ёмкость можно определить по следующей формуле: Эпсилон нулевое - это электрическая постоянная. Судя из данной формулы, можно сделать вывод, что емкость сферического проводника зависит исключительно от внешнего диэлектрика, а также от радиуса сферы, то есть её размера. То есть, чем больше сфера, тем больше её емкость. Иными словами можно сказать, что ёмкость - это некая тара, которая вмещает в себя величину заряда. Итак, Ёмкость - это некая ФВ, позволяющая определить величину заряда, необходимую для изменения потенциала проводника на 1 В. Ёмкость измеряется в фарадах (Ф). Самым главным для нас сферическим проводником является Земля. Посчитать её емкость достаточно просто. Если принять радиус за 6400 км, а окружающую диэлектрическую среду мы знаем - это воздух, то получим: Самым простым примером для исследования конденсаторов являются плоские конденсаторы. Структура плоского конденсатора достаточно проста. Он состоит из двух металлических плоскостей (обкладок), которые параллельно расположены друг к другу, и располагаются на некотором расстоянии. Между данными пластинами имеется диэлектрик. Самым простым примером плоского конденсатора является тот, у которого в виде диэлектрика воздух, то есть Ɛ = 1. Обе обкладки имеют противоположный заряд -q, +q. Схематически конденсатор изображают следующим образом: Следует отметить, что поле в конденсаторе показывается линиями, выходящими из положительно заряженной пластины, и входящими в отрицательно заряженную пластину. Для определения его ёмкости следует воспользоваться следующей формулой: Как уже говорилось раньше, ёмкость зависит исключительно от геометрических размеров конденсатора, а также от диэлектрика между пластинами. cknow.ru36. Электроемкость уединенного проводника. Электроемкость уединенного шара. Электроемкость плоского конденсатора
6. Электроемкость. Конденсаторы. Емкость плоского конденсатора
7. Соединение конденсаторов. Энергия заряженного конденсатора
8. Закон Ома для однородного участка цепи. Сопротивление проводников
36. Электроемкость уединенного проводника. Электроемкость уединенного шара.
37. Конденсаторы. Электроемкость плоского конденсатора (вывод). Соединение конденсаторов.
Что такое электроемкость конденсатора? :: SYL.ru
Соединение конденсаторов
Виды конденсаторов
Электроемкость плоского конденсатора
Сферический конденсатор
Цилиндрический конденсатор
Повреждения в конденсаторах
Меры предосторожности
7.2. Электроемкость плоского конденсатора
Электроемкость конденсатора, теория и примеры
![Rendered by QuickLaTeX.com \[C=\frac{q}{U}=\frac{q}{{\varphi}_1-{\varphi}_2} \qquad (1) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-eb02c51776a8a3e24b9c5899a3f5df9b_l3.png)
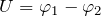 – разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
– разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора. раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью
раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью  . Значит емкость конденсатора с диэлектриком (C) в
. Значит емкость конденсатора с диэлектриком (C) в  раз больше, чем электроемкость воздушного конденсатора (
раз больше, чем электроемкость воздушного конденсатора (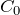 ):
):![Rendered by QuickLaTeX.com \[C=\varepsilon C_0 \qquad (2) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-929d46afde6c82a50b57be36cbd5f212_l3.png)
 – диэлектрическая проницаемость диэлектрика.
– диэлектрическая проницаемость диэлектрика.Электроемкость плоского конденсатора
![Rendered by QuickLaTeX.com \[C=\frac{\varepsilon {\varepsilon}_0S}{d} \qquad (3) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1bb3b9d5633a67217e93b838682e6374_l3.png)
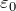 – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
– электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.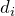 , соответствующая диэлектрическая проницаемость i-го слоя
, соответствующая диэлектрическая проницаемость i-го слоя 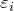 , равна:
, равна:![Rendered by QuickLaTeX.com \[C=\frac{{\varepsilon}_0S}{\sum^N_{i=1}{\frac{d_i}{{\varepsilon}_i}}} \qquad (4) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-600defe3ac03320da565bd86a0b5038b_l3.png)
Электрическая емкость цилиндрического конденсатора
![Rendered by QuickLaTeX.com \[C=\frac{2\pi \varepsilon {\varepsilon}_0l}{ln\left(\frac{R_2}{R_1}\right)} \qquad (5) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-92afa96d24e5898a1aff2be5a90c4c3a_l3.png)
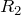 – радиус внешней обкладки;
– радиус внешней обкладки; 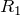 – радиус внутренней обкладки.
– радиус внутренней обкладки.Емкости сферического конденсатора
![Rendered by QuickLaTeX.com \[C=\frac{4\pi \varepsilon {\varepsilon}_0R_1R_2}{R_2-R_1} \qquad (6) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-95f67890417854cb46f40711f82f186a_l3.png)
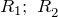 – радиусы обкладок конденсатора.
– радиусы обкладок конденсатора.Примеры решения задач
Электроемкость конденсатора
Постоянный электрический ток
3.1.9 Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Видеоурок 1: Емкость конденсатора - Физика в опытах и экспериментах
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''






Поделиться с друзьями: