ПРАКТИЧАСКАЯ РАБОТА №1 «Расчет эквивалентной емкости при смешанном соединении конденсаторов, а также распределения зарядов и напряжений» На рисунке 1 дана схема соединения конденсаторов. Значение емкостей конденсаторов и значение одного из напряжений или зарядов для своего варианта взять из таблицы 1. Вычислить эквивалентную емкость батареи конденсаторов; напряжение сети, напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей, а также потенциал заданной точки. Рисунок 1 Таблица 1 № вар. Емкость конденсатора, мкФ Напряжение, заряд Точка, потенциал которой следует вычислить С1 С2 С3 С4 С5 1 120 280 16 80 70 U=20 В Б 2 600 200 150 400 200 Q3=72∙10-4 Кл Б 3 24 12 2 16 14 U5=25 В А 4 30 20 12 20 16 Q4=4∙10-4 Кл Б 5 10 15 24 6 9 U1=15 В А 6 12 6 5 9 9 Q2=282∙10-6 Кл А 7 30 15 10 65 15 Q5=6∙10-4 Кл А 8 18 9 12 15 21 U2=84 В Б 9 140 60 6 30 18 U3=50 В А 10 150 50 37,5 30 20 Q1=3∙10-4 Кл Б 11 200 300 40 160 100 U=40 В Б 12 540 150 90 380 120 Q3=54∙10-4 Кл А 13 46 26 8 34 28 U5=45 В Б 14 60 45 25 40 30 Q4=8∙10-4 Кл А 15 30 25 46 20 18 U1=30 В Б 16 25 15 10 20 15 Q2=564∙10-6 Кл Б 17 60 30 45 120 25 Q5=15∙10-4 Кл Б 18 36 18 24 30 44 U2=160 В А 19 300 140 12 50 38 U3=100 В Б 20 280 100 70 65 45 Q1=6∙10-4 Кл А 21 60 150 9 40 25 U=10 В Б 22 300 100 70 200 90 Q3=36∙10-4 Кл А 23 14 6 4 8 10 U5=15 В А 24 90 60 25 40 26 Q4=12∙10-4 Кл Б 25 6 8 12 4 12 U1=7 В А 26 46 18 15 27 18 Q2=846∙10-6 Кл Б 27 90 45 30 190 65 Q5=18∙10-4 Кл А 28 560 35 25 45 20 U2=320 В А 29 400 240 15 35 100 U3=150 В А 30 390 150 200 90 180 Q1=9∙10-4 Кл Б ПРИМЕР На рисунке 2 приведена схема соединения конденсаторов. Определить эквивалентную емкость Сэкв батареи конденсаторов, общий заряд Q, напряжение сети U, напряжение и заряд на каждом конденсаторе, если дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; напряжение на пятом конденсаторе U5=30 В. Рисунок 2 Дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; U5=30 В Определить: U, Q, Сэкв, U1, U2, U3, U4, Q1. Решение: 1. Общая емкость последовательно соединенных конденсаторов С4 и С5: 2. Общая емкость параллельно соединенных конденсаторов С3 иС4,5: 3. Общая емкость последовательно соединенных конденсаторов С1, С2 и С3,4,5, которая и является эквивалентной емкостью батареи конденсаторов: 4. По заданному напряжению U5 и емкости конденсатора С5 определяем заряд, накапливаемый этим конденсатором: 5. Заряд конденсатора С4 Q4=Q5=Q4,5=180・10-6 Кл, т. к. конденсаторы С4 и С5 соединены последовательно. 6. Напряжение на четвертом конденсаторе: 7. Напряжение на третьем конденсаторе: 8. Заряд конденсатора С3: 9. Общий заряд батареи и заряды конденсаторов С1 и С2: 10. Напряжение на первом и втором конденсаторах: 11. Напряжение сети (напряжение последовательно соединенных конденсаторов С1, С2, С3,4,5): 12. Энергия электрического поля батареи: studfiles.net «Физика - 10 класс» «Электроёмкость» — последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22). Задача 1. Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C1 = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Р е ш е н и е. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С2 - C)U = (nC1 - C1)U = (п — 1)С1U = 10-8 Кл. Изменение энергии электрического поля Задача 2. Заряд конденсатора q = 3 • 10-8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона Р е ш е н и е. Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А — работа электрического поля конденсатора: Следовательно, Окончательно Задача 3. Четыре конденсатора ёмкостями С1 = С2 = = 1 мкФ, С3 = 3 мкФ, С4 = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов. Р е ш е н и е. Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С2,3 = С2 + С3, а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С1, С2,3, С4, найдём из соотношения 1/Cэкв = 1 /С1 + 1/С2,3 + 1 /С4, Сэкв = (4/7) • 10-6 Ф. Заряды на этих конденсаторах одинаковы: q1 = q2,3 = q4 = Сэкв = 8 • 10-5 Кл. Следовательно, заряд первого конденсатора q1 = 8 • 10-5 Кл, а разность потенциалов между его обкладками, или напряжение, U1 = q1/С1 = 80 В. Для четвёртого конденсатора аналогично имеем q4 = 8 • 10-5 Кл, U4 = q4/C4 = 40 В. Найдём напряжение на втором и третьем конденсаторах: U2 = U3 = q2,3/C2,3 = 20 В. Таким образом, на втором конденсаторе заряд q2 = C2U2 = 2 • 10-5 Кл, а на третьем конденсаторе q3 = C3U3 = 6 • 10-5 Кл. Отметим, что q2,3 = q2 + g3. Задача 4. Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны. Р е ш е н и е. Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов. В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φA ≠ φB в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и Сэкв определим по формуле 1/Сэкв = 1/2С1 + 1/2С2, откуда Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно, Эквивалентные конденсаторы с С'экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости: Задача 5. Энергия плоского воздушного конденсатора W1 = 2 • 10-7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если: 1) конденсатор отключён от источника питания; 2) конденсатор подключён к источнику питания. Р е ш е н и е. 1) Так как конденсатор отключён от источника питания, то его заряд q0 остаётся постоянным. Энергия конденсатора до заполнения его диэлектриком после заполнения где С2 = εС1. Тогда Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский Электростатика - Физика, учебник для 10 класса - Класс!ная физика Что такое электродинамика --- Электрический заряд и элементарные частицы. Закон сохранения заряд --- Закон Кулона. Единица электрического заряда --- Примеры решения задач по теме «Закон Кулона» --- Близкодействие и действие на расстоянии --- Электрическое поле --- Напряжённость электрического поля. Силовые линии --- Поле точечного заряда и заряженного шара. Принцип суперпозиции полей --- Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» --- Проводники в электростатическом поле --- Диэлектрики в электростатическом поле --- Потенциальная энергия заряженного тела в однородном электростатическом поле --- Потенциал электростатического поля и разность потенциалов --- Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности --- Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» --- Электроёмкость. Единицы электроёмкости. Конденсатор --- Энергия заряженного конденсатора. Применение конденсаторов --- Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора» Вверх class-fizika.ru Цель: закрепить знания методов расчета электрической емкости и зарядов конденсаторов при их смешанном соединении. Электрический конденсатор — это система из двух проводников (обкладок, пластин), разделенных диэлектриком. Конденсаторы обладают свойством накапливать на своих обкладках электрические заряды, равные по величине и противоположные по знаку. Электрический заряд q каждой из обкладок пропорционален напряжению U между ними: Величину С, равную отношению заряда одной из обкладок конденсатора к напряжению между ними, называют электрической емкостью конденсатора и выражают в фарадах (Ф). Емкость конденсатора зависит от геометрических размеров, формы, взаимного расположения и расстояния между обкладками, а также от свойств диэлектрика. Конденсаторы могут быть соединены последовательно, параллельно и смешанно (последовательно-параллельно). Последовательное соединение При таком на обкладках всех конденсаторов будут одинаковые по величине заряды: Напряжения на конденсаторах будут различны, так как они зависят от их емкостей: Общее напряжение: Общая, или эквивалентная, емкость Параллельное соединение При параллельном соединении напряжение на всех конденсаторах одинаковое. Заряды на обкладках отдельных конденсаторов при различной их емкости: Заряд, полученный всеми параллельно соединенными конденсаторами: Общая (эквивалентная) емкость: Задание 1. Определить эквивалентную емкость батареи конденсаторов, соединенных по схеме, при соответствующих положениях ключей. 2. Для случая, когда ключи К1, К2 и К3 разомкнуты, найти заряды на каждом конденсаторе и общий заряд схемы. Порядок выполнения расчета Задание 1 1. Для своих данных начертить исходную схему. 2. Рассчитать последовательное соединение С3-С7: 3. Рассчитать параллельное соединение С4-С5: 4. Рассчитать последовательное соединение С2-С45: 5. Найти эквивалентную емкость, рассчитав параллельное соединение С245-С37: Задание 2 1. Для своих данных начертить исходную схему. 2. Рассчитать заряды на каждом конденсаторе: 3. Рассчитать общий заряд схемы: 4. Проверка: viktakhram.wixsite.com Конденсаторы являются неотъемлемой частью электрических схем. В большинстве случаев оперируют такими понятиями, как емкость и рабочее напряжение. Эти параметры являются основополагающими. Конденсаторы различных типов В некоторых случаях для более полного понимания работы упомянутого элемента необходимо иметь представление, что означает энергия заряженного конденсатора, как она вычисляется и от чего зависит. Наиболее просто вести рассуждения применительно к плоскому конденсатору. В основе его конструкции лежат две металлических обкладки, разделенные тонким слоем диэлектрика. Плоский конденсатор Если подключить емкость к источнику напряжения, то нужно обратить внимание на следующее: Данные соображения позволяют сделать вывод, что формулу энергии заряженного конденсатора можно получить несколькими способами. Энергия заряженного плоского конденсатора наиболее просто определяется, исходя из работы по сближению обкладок. Рассмотрим силу притяжения единичного заряда одной из обкладок к противоположной: F=q0E. В данном выражении q0 – величина заряда, E – напряженность поля обкладки. Поскольку напряженность электрического поля определяется из выражения: E=q/(2ε0S), где: формулу силы притяжения можно записать как: F=q0 q/(2ε0S). Для всех зарядов сила взаимодействия между обкладками, соответственно, составляет: F=q2/(2ε0S). Работа по сближению пластин равняется произведению силы взаимодействия на пройденное расстояние. Таким образом, энергия заряженного конденсатора определяется выражением: W=A=Fd. Важно! В приведенном выражении должна быть разница в положениях пластин. Записывая только одну величину d, подразумеваем, что конечным результатом будет полное сближение, то есть d2=0. С учетом предыдущих выражений можно записать: W=d q2/(2ε0S). Известно, что емкость плоского конденсатора определяется из такого выражения: C=d/(ε0S). В результате энергия определяется как: W=q2/(2С). Полученное выражение неудобно тем, что вызывает определенные затруднения определения заряда на обкладках. К счастью, заряд, емкость и напряжение имеют строгую взаимосвязь: q = С U. Теперь выражение принимает полностью понятный вид: W=CU2/2. Полученное выражение справедливо для конденсаторов любых типов, не только плоских, и позволяет без затруднений в любой момент времени определять накопленную энергию. Емкость обозначается на корпусе и является величиной постоянной. В крайнем случае ее несложно измерять, используя специальные приборы. Напряжение измеряется вольтметром с необходимой точностью. К тому же очень просто зарядить конденсатор не полностью (меньшим напряжением), снизив, таким образом, запасенную энергию. В большинстве случаев применения емкостей в электрических цепях понятие энергии не употребляется. Особенно это относится к время,- и частотозадающим цепям, фильтрам. Но есть области, где необходимо использовать накопители энергии. Наиболее яркий пример –фотографические вспышки. В накопительном конденсаторе энергия источника питания накапливается сравнительно медленно – несколько секунд, но разряд происходит практически мгновенно через электроды импульсной лампы. Конденсатор, подобно аккумулятору, служит для накопления электрического заряда, но между этими элементами есть много различий. Емкость аккумулятора несравненно выше, чем у конденсатора, но последний способен отдать ее практически мгновенно. Лишь недавно, с появлением ионисторов, это различие несколько сгладилось. Ионистор Какова же ориентировочная величина энергии? Можно для примера вычислить ее для уже упомянутой фотовспышки. Пускай, напряжение питания составляет 300 В, а емкость накопительного конденсатора – 1000 мкФ. При полном заряде величина энергии составит 45 Дж. Это довольно большая величина. Прикосновение к выводам заряженного элемента может привести к несчастному случаю. Конденсатор фотовспышки Важно! Принудительный разряд путем закорачивания выводов металлическими предметами чреват выходом устройства из строя. Накопленная энергия конденсатора способна за долю секунды расплавить выводы внутри элемента и вывести его из строя. elquanta.ru · Фарада — очень крупная единица емкости, которая практически не применяется. Обычно пользуются более мелкими единицами емкости: микрофарадой (мкф) и пикофарадой (пф). · Фарада содержит миллион микрофарад: 1ф=106 мкф. Микрофарада содержит миллион пикофарад: 1 мкф=106 пф. · Емкость конденсатора зависит от площади его пластин. При одном и том же напряжении и одинаковом расстоянии между пластинами конденсатор, у которого пластины имеют большую площадь, заряжается большим количеством электричества и в связи с этим обладает большей емкостью, чем такой же конденсатор с тем же диэлектриком, но с пластинами малого размера. · Емкость конденсатора зависит от расстояния между его пластинами (от толщины диэлектрика). Конденсатор, у которого пластины находятся на большом расстоянии друг от друга, обладает меньшей емкостью, чем такой же конденсатор, пластины которого сближены. Это объясняется тем, что при малом расстоянии между пластинами взаимодействие их разноименных зарядов сильнее, а потому конденсатор накапливает большее количество электричества. · Емкость конденсатора зависит от свойств материала диэлектрика—от его диэлектрической проницаемости. Например, при равных размерах пластин и равном расстоянии между ними конденсатор, у которого диэлектриком является слюда, имеет примерно в шесть раз большую емкость, чем конденсатор с воздушным диэлектриком. При тех же условиях бумажный конденсатор имеет в 2,2 раза большую емкость, чем воздушный, но меньшую, чем слюдяной. · I Для вычисления емкости плоского конденсатора, имеющего две пластины, служит формула · · где С — емкость конденсатора, пф, · S — поверхность одной пластины, см2, · d — расстояние между пластинами, см, · — диэлектрическая проницаемость (см. табл. 1), · 0,09 — постоянный коэффициент, переводящий емкость в пикофарады. · Пример. Конденсатор имеет две пластины. Площадь каждой пластины составляет 15 см2. Между пластинами помещен диэлектрик — пропарафинированная бумага толщиной 0,02 см. Вычислить емкость этого конденсатора. · Решение. Из табл. 1 следует, что диэлектрическая проницаемость, пропарафинированной бумаги =2,2. · Емкость конденсатора · · § 10. ЗАРЯД И РАЗРЯД КОНДЕНСАТОРА · · Конденсатор накапливает электрические заряды — заряжается. Накопление зарядов происходит в том случае, если конденсатор подключить к источнику электрической энергии. · · Свободные электроны с отрицательного полюса батареи переместятся на левую пластину конденсатора и на ней появится избыток электронов — отрицательный заряд. · Таким образом, в проводах, соединяющих пластины конденсатора с батареей, будет протекать электрический ток. Если между конденсатором и батареей не включено большое сопротивление, то время заряда конденсатора очень мало и ток в проводах протекает кратковременно. · При заряде конденсатора энергия, сообщаемая батареей, переходит в энергию электрического поля, возникающего между пластинами конденсатора. · Процесс разряда конденсатора (см. рис. 6). Если ключ установить на контакт 2, пластины заряженного конденсатора окажутся соединенными между собой. При этом произойдет разряд конденсатора и исчезнет электрическое поле между его пластинами. · При разряде конденсатора избыточные электроны с левой пластины переместятся по проводам к правой пластине, где их недостает; когда количество электронов на пластинах конденсатора станет одинаковым, процесс разряда закончится и ток в проводах исчезнет. · Энергия электрического поля конденсатора при его разряде расходуется на работу, связанную с перемещением зарядов,— на создание электрического тока. · Время разряда конденсатора через провода, обладающие малым сопротивлением, также весьма мало. · Процесс заряда и разряда конденсатора широко используется в различных устройствах. · Наиболее широко распространены бумажные, слюдяные и электролитические конденсаторы постоянной ёмкости. · Бумажный конденсатор КБГ. Бумажный конденсатор (рис.7) представляет собой металлический корпус 1, в котором герметически закрыт пакет 2, состоящий из пластин, выполненных в виде алюминиевой фольги 2 и изолированных одна от другой тонкой бумагой 4, пропитанной изоляционным материалом (церезином, головаксом). Пластины конденсатора присоединяются к выводным лепесткам 3, изолированным от корпуса. · Слюдяной конденсатор КСО. Слюдяной конденсатор (рис. 7, б) состоит из двух пакетов металлических пластин и слюдяных прокладок. Между каждой парой пластин, принадлежащих разным пакетам, помещается тонкая прокладка из слюды. Собранные таким образом конденсаторы запрессовываются в пластмассу, из которой выходят наружу два лепестка по одному от каждого пакета пластин. Они служат для включения конденсатора в схему. · Электролитический конденсатор КЭ-2М. Электролитический конденсатор (рис. 7, в) представляет собой алюминиевый стакан 6, в котором помещаются две алюминиевые ленты, скатанные в рулон. Между лентами проложена фильтровальная бумага, пропитанная электролитом.. Одна алюминиевая лента соединяется с корпусом стакана, а вторая -—с контактом 7, укрепленным на его верхней крышке. При заряде конденсатора на поверхности алюминиевых лент, подключаемых к положительному полюсу источника тока, образуется пленка окиси алюминия, являющаяся диэлектриком. Так как эта пленка очень тонкая, то емкость электрических кондесаторов относительно велика. Электролитические конденсаторы изготовляют емкостью до 2000 мкф при рабочем напряжении до 500 в. · · Рис 7 Конденсаторы постоянной емкости: · а-бумажный КБГ, б-слюдяной КСО, в — электролитический КЭ-2М и его условное обозначение · · Рис 8 Конденсаторы переменной (а) и полупеременной (б) · емкости и их условное обозначение: · 1 — ротор, 2 — статор, 3 — гайка крепления · Конденсаторы переменной емкости. Конденсаторы, емкость которых можно изменять, называются конденсаторами переменной емкости (рис. 8, а). Такой конденсатор состоит из неподвижных пластин (статора) и подвижных пластин (ротора), укрепленных на оси. При плавном повороте оси подвижные пластины в большей или меньшей степени входят в промежутки между неподвижными пластинами, не касаясь их, и емкость конденсатора плавно увеличивается. Когда подвижные пластины полностью входят в промежутки между неподвижными пластинами, емкость конденсатора достигает наибольшей величины. · Разновидностью конденсатора переменной емкости является конденсатор полупеременной емкости (рис. 8, б). Такой конденсатор имеет неподвижную (статор) и подвижную (ротор) пластины. Основание пластин изготовлено из керамики, а на него нанесен слой серебра. · Ротор укреплен с помощью винта. Поворачивая винт, перемещают ротор и при этом изменяется емкость конденсатора в пределах 2—30 пф. · §11. СОЕДИНЕНИЯ КОНДЕНСАТОРОВ · · Если необходимо увеличить общую емкость конденсаторов, то их соединяют между собой параллельно (рис. 9, а). При этом способе соединения общая площадь пластин увеличивается по сравнению с площадью пластины каждого конденсатора. Общая емкость конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов и вычисляется по формуле · Собщ=С1 + С2+С3+ ••• (10) · Это можно подтвердить следующим образом. · fiziku5.ru «Электроёмкость» - последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22). Задача 1. Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C 1 = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля. Р е ш е н и е. Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq - (С 2 - C)U = (nC 1 - C 1)U = (п - 1)С 1 U = 10 -8 Кл. Задача 2. Заряд конденсатора q = 3 10 -8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона Р е ш е н и е. Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А - работа электрического поля конденсатора: Следовательно, Окончательно Задача 3. Четыре конденсатора ёмкостями С 1 = С 2 = = 1 мкФ, С 3 = 3 мкФ, С 4 = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов. Р е ш е н и е. Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С 2,3 = С 2 + С 3 , а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С 1 , С 2,3 , С 4 , найдём из соотношения 1/Cэкв = 1 /С 1 + 1/С 2,3 + 1 /С 4 , Сэкв = (4/7) 10 -6 Ф. Заряды на этих конденсаторах одинаковы: q 1 = q 2,3 = q 4 = Сэкв = 8 10 -5 Кл. Следовательно, заряд первого конденсатора q 1 = 8 10 -5 Кл, а разность потенциалов между его обкладками, или напряжение, U 1 = q 1 /С 1 = 80 В. Для четвёртого конденсатора аналогично имеем q 4 = 8 10 -5 Кл, U 4 = q 4 /C 4 = 40 В. Найдём напряжение на втором и третьем конденсаторах: U 2 = U 3 = q 2,3 /C 2,3 = 20 В. Таким образом, на втором конденсаторе заряд q 2 = C 2 U 2 = 2 10-5 Кл, а на третьем конденсаторе q 3 = C 3 U 3 = 6 10 -5 Кл. Отметим, что q 2,3 = q 2 + g 3 . Задача 4. Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны. Р е ш е н и е. Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов. В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φ A ≠ φ B в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и С экв определим по формуле 1/С экв = 1/2С 1 + 1/2С 2 , откуда Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, сле stroypoz.ruЗаряд и разряд конденсатора. Определить заряд и напряжение каждого конденсатора
Пр. 1. конденсаторы
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»





Устали? - Отдыхаем!


Практическая работа №1 Расчет смешанного соединения конденсаторов
Теоретические сведения
Формула расчета энергии конденсаторов, как зарядить плоский конденсатор
Определение понятия энергии
Вывод формулы
Для чего необходимо знать энергию
Видео
Оцените статью: Заряд и разряд конденсатора - fiziku5.ru

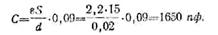
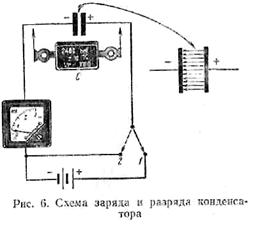 Процесс заряда конденсатора (рис. 6). При установке ключа на контакт 1 пластины конденсатора окажутся подключенными к батарее и на них появятся противоположные по знаку электрические заряды («+» и «—»). Произойдет заряд конденсатора и между его пластинами возникнет электрическое поле. При заряде конденсатора свободные электроны правой пластины переместятся по проводнику в направлении положительного полюса батареи и на этой пластине останется недостаточное количество электронов, в результате чего она приобретет, положительный заряд.
Процесс заряда конденсатора (рис. 6). При установке ключа на контакт 1 пластины конденсатора окажутся подключенными к батарее и на них появятся противоположные по знаку электрические заряды («+» и «—»). Произойдет заряд конденсатора и между его пластинами возникнет электрическое поле. При заряде конденсатора свободные электроны правой пластины переместятся по проводнику в направлении положительного полюса батареи и на этой пластине останется недостаточное количество электронов, в результате чего она приобретет, положительный заряд.
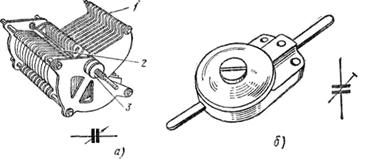
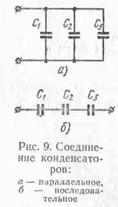 Соединенные параллельно конденсаторы находятся под одним и тем же напряжением, равным U вольт, а общий заряд этих конденсаторов равен q кулонов. При этом каждый конденсатор соответственно получает заряд q1, q2, q3, и т. д. Следовательно,
Соединенные параллельно конденсаторы находятся под одним и тем же напряжением, равным U вольт, а общий заряд этих конденсаторов равен q кулонов. При этом каждый конденсатор соответственно получает заряд q1, q2, q3, и т. д. Следовательно,Определить заряд и напряжение каждого конденсатора. Последовательное соединение конденсаторов
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''











Поделиться с друзьями: