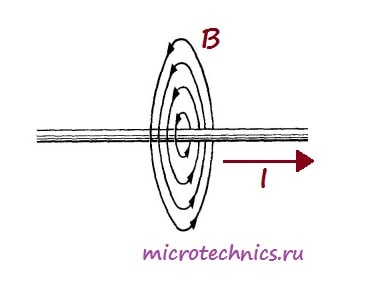
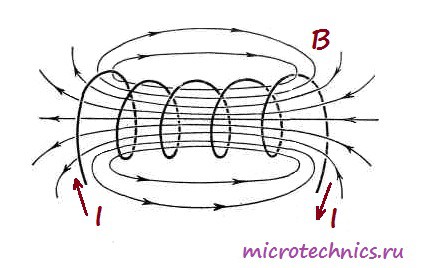
Словосочетание «катушка ниток» знакомо всем, но про катушку индуктивности слышали, думаю, не все. Вот что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь фиговинка, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции. Изоляция может быть из бесцветного лака, из проводной изоляции, и даже из матерчатой. Тут фишка такая, хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности сами, ни в коем случае не вздумайте брать обычный медный голый провод! Любая катушка индуктивности, как ни странно, обладает индуктивностью 🙂 Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется LC — метром. Что такое индуктивность? Давайте разбираться. Если через проводок прогнать электрический ток, то он вокруг себя создаст магнитное поле: где В — магнитное поле , I — сила тока. А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы электрический ток: И у нас получилась вот такая картина с магнитными силовыми линиями: Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, получается площадь цилиндра, тем больше будет магнитный поток (Ф). Так как по всей этой конструкции течет электрический ток, то значит в этот момент он обладает какой-то Силой тока (I). А коэффициент между магнитным потоком и силой тока называется индуктивностью, и вычисляется так: С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается — магнитное поле сжимается. Катушка индуктивности обладает также очень интересными свойствами. При подаче на катушку электрического тока постоянного напряжения, в катушке возникает напряжение, противоположное напряжению электрического тока и оно потом исчезает через несколько долей секунд. Это противоположное напряжение называется ЭлектроДвижущейСилой самоиндукции, или просто — ЭДС самоиндукции. Это ЭДС зависит от индуктивности катушки. Поэтому в момент подачи напруги на катушку Сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение,в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения, согласно Закон Ома: где I — сила тока в катушке, U — напряжение в катушке, R — сопротивление катушки. Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки постоянное. И второй прикол в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет приплюсовываться к напряжению, которое мы подали на катушку. Следовательно и ток будет в самом начале больше, а потом тихонько спадет до нуля. Время спада силы тока также зависит от индуктивности катушки. Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока резко возрастет в катушке и плавно убавиться до нуля. Короче говоря,сила тока в катушке мгновенно измениться не может. Это в электронике называют первым законом коммутации. Уфф, ну все, самое тяжелое позади :-). Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником. Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллиГенри. А вот катушки индуктивности с сердечником: В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра. Для катушек средней индуктивности используются ферритовые сердечники: Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но есть одно различие: у них имеется только одна первичная обмотка: От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль. Имеется ферритовый сердечник Начинаю вводить катушку в сердечник на самый край LC-метр показывает 21 микроГенри. Ввожу катушку на середину феррита 35 микроГенри. Уже лучше. Продолжаю вводить катушку на правый край феррита 20 микроГенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности: где 1 — это каркас катушки 2 — это витки катушки 3 — сердечник, у которого сверху пазик по маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки. Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки Индуктивность стала почти 50 микроГенри! А давайте-ка попробуем расправим витки по всему ферриту 13 микроГенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку». Убавим витки катушки в два раза. Было 24 витка, стало 12. Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность. Индуктивность меняется не прямолинейно виткам. Давайте поэкспериментируем с ферритовым кольцом. Замеряем индуктивность 15 микроГенри Отдалим витки катушки друг от друга Замеряем снова Хм, также 15 микроГенри. Делаем вывод: расстояние от витка до витка не играет никакой роли катушки индуктивности в тороидальном сердечнике. Мотанем побольше витков. Было 3 витка, стало 9. Замеряем Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам. Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки. Остальные факторы мы разобрали в опытах. Более подробно про формулы расчета здесь. Но лучше все таки изготовить катушку опытным путем с замером ее индуктивности на каждом этапе. На схемах катушки индуктивности обозначаются вот так: При последовательном соединении индуктивностей, их общая индуктивность равна сумме индуктивностей. А при параллельном соединении получаем вот так: При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неправильны. Не ставьте на одну железную оську два и более тороидальных катушек, это может привести к неправильным показаниям общей индуктивности. Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот. Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ сигналов). На низких частотах (НЧ частоты) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели: Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции более эффективны. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике. Катушка индуктивности играет в электронике очень большую роль, особенно в приемо-передающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока. Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке: www.ruselectronic.com Приветствую всех на нашем сайте! Мы продолжаем изучать электронику с самого начала, то есть с самых основ и темой сегодняшней статьи будет принцип работы и основные характеристики катушек индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы. Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку :), то есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас: Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле: А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку: В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле: Давайте разберемся, что за величину входят в это выражение: Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки. С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный 🙂 Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь: Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель? Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом: Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать. Напряжения на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока). Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи: После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает). Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки: На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока. Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток: Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так: Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока: Собственно, график нам и демонстрирует эту зависимость 🙂 Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения. Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂 Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: Где Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный ( Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение А следовательно: Построим на одном графике зависимости тока и напряжения в цепи от времени: Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности: При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода. Вот и с включением катушки в цепь переменного тока мы разобрались 🙂 На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому дальнейший разговор о катушках индуктивности мы будем вести в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте! microtechnics.ru Не так давно, мы с вами рассматривали, как ведет себя конденсатор в цепи постоянного и переменного тока. А в этой статье рассмотрим, как ведет себя катушка индуктивности, если на нее подать постоянный и переменный ток. Хочу вам напомнить, что постоянный ток — это ток, который течет всегда в одном направлении, а переменный ток — это ток, который меняет свое направление с какой-то частотой. Катушка индуктивности в цепи постоянного тока. Итак, для этого опыта нам понадобится блок питания, который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности. Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник: Намотать на него лакированного медного провода и зачистить выводы: Замеряем индуктивность нашей катушки с помощью LC метра: 132 микроГенри. Теперь собираем все это вот по такой схеме: где L — катушка индуктивности La — лампочка накаливания на напряжение 12 Вольт Bat — блок питания, с выставленным напряжением 12 Вольт Лампочка засветилась! Как вы помните, конденсатор у нас не пропускал постоянный электрический ток: Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам провод, из которого сделана катушка. Катушка индуктивности в цепи переменного тока. Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом. Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом. Собираем все это дело по такой схеме: Получилось как то так: Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора. Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе. Кто до сих пор не знает что такое осциллограф, можно прочитать про него здесь. Что такое цифровой осциллограф, можно прочитать здесь. Про автоматическое измерение параметров с помощью цифрового осцилла, читаем здесь. Кто уже читал и все знает, идем дальше. Для начала подаем сигнал с частотой в 1 КилоГерц. Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F (частота) =1 КилоГерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F=1 КилоГерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе. Увеличиваем частоту до 10 КилоГерц Амплитуда не уменьшилась. Сигнал какой есть, такой и остался. Увеличиваем до 100 КилоГерц Видели да? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду. Сдвиг фаз — это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз: Увеличиваем частоту до 200 КилоГерц На частоте 200 КилоГерц амплитуда упала вдвое, да и разность фаз стала больше. Увеличиваем частоту до 300 КилоГерц. Амплитуда желтого сигнала упала уже до 720 миллиВольт. Разность фаз стала еще больше. Увеличиваем частоту до 500 КилоГерц Амплитуда уменьшилась до 480 миллиВольт. Добавляем еще частоту до 1 МегаГерца Амплитуда желтого канала стала 280 миллиВольт. Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 МегаГерца Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить на осцилле в 5 раз. И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2. Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок: Так какой вывод можно сделать? С увеличением частоты сопротивление катушки растет, а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов. Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микроГенри. Итак, прогоняем все по тем же значениям частоты При частоте в 1 КилоГерц у нас значение почти не изменилось. 10 КилоГерц Здесь тоже ничего не изменилось. 100 КилоГерц Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонька сдвигаться. 200 КилоГерц Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты. 300 КилоГерц Сдвиг фаз стал больше и амплитуда просела еще больше 500 КилоГерц Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела. 1 МегаГерц Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉 2 МегаГерца, предел моего генератор частоты Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта. Обратите внимание на амплитуду в Вольтах на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом. Отсюда вывод напрашивается сам собой: При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается. С помощью нехитрых умозаключений, физиками была выведена формула: где ХL — сопротивление катушки, Ом П — постоянная и равна приблизительно 3,14 F — частота, Гц L — индуктивность В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда и мощность на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука. www.ruselectronic.com Катушка индуктивности —винтовая,спиральнаяили винтоспиральная катушка из свёрнутого изолированногопроводника, обладающая значительнойиндуктивностьюпри относительно малойёмкостии маломактивном сопротивлении. Такая система способна накапливать магнитнуюэнергиюпри протеканииэлектрического тока. Устройство обычно представляет собой винтовую,спиральнуюили винтоспиральную катушку из одножильного или многожильного изолированногопровода, намотанного на цилиндрический, тороидальный или прямоугольный каркас издиэлектрикаили плоскую спираль, волну или полоску печатного или другого проводника. Также бывают и бескаркасные катушки. Намотка может быть как однослойной (рядовая и с шагом), так и многослойная (рядовая, внавал, «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость. Для увеличения индуктивности применяют сердечники из ферромагнитныхматериалов: электротехнической стали,пермаллоя, карбонильного железа,ферритов. Также сердечники используют для изменения индуктивности катушек в небольших пределах. Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению. Катушка индуктивности обладает реактивным сопротивлением величина которого равна: , где— индуктивность катушки,—циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление. При протекании тока катушка запасает энергию, равную работе, которую необходимо совершить для установления текущего тока . Величина этой энергии равна При изменении тока в катушке возникает ЭДС самоиндукции, значение которой Индуктивность катушки пропорциональна линейным размерам катушки, магнитной проницаемостисердечника и квадрату числа витков намотки. Индуктивность катушки, намотанной натороидальномсердечнике где: μ0—магнитная постоянная μi—магнитная проницаемостьматериала сердечника (зависит от частоты) se— площадь сечения сердечника le— длина средней линии сердечника N— число витков При последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек. При параллельном соединении катушек общая индуктивность равна В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых сопротивление катушки не является чисто реактивным. Наличие паразитных эффектов ведёт к появлению потерь в катушке, оцениваемых сопротивлением потерь . Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране. Потери в проводах вызваны тремя причинами: Во-первых, провода обмотки обладают омическим (активным) сопротивлением. Во-вторых, сопротивление провода обмотки переменному току возрастает с ростом частоты, что обусловлено скин-эффектом, суть которого состоит в том, что ток протекает не по всему сечению проводника, а по кольцевой части поперечного сечения. В третьих, в проводах обмотки, свитой в спираль, проявляется эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токови магнитного поля к периферии провода, прилегающей к каркасу, в результате чего сечение, по которому протекает ток, принимает серповидный характер, что ведёт к дополнительному возрастанию сопротивления провода. Потери в диэлектрике обусловлены тем, что между соседними витками катушки существует паразитная ёмкость, что приводит к утечкам переменного тока между витками. Потери в экране обусловлены тем, что ток, протекающий по катушке, индуцирует ток в экране. С сопротивлениями потерь тесно связана другая характеристика — добротность. Добротность катушки индуктивности определяет отношение между активным и реактивным сопротивлениями катушки. Добротность равна Практически величина добротности лежит в пределах от 30 до 200. Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями, намоткой вида «универсаль», применением посеребрёного провода, применением многожильного провода вида «литцендрат». ТКИ — это параметр, характеризующий зависимость индуктивности катушки от температуры. Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки. Контурные катушки индуктивности Эти катушки используются совместно с конденсаторамидля получения резонансных контуров. Они должны иметь высокую стабильность, точность идобротность. Катушки связи Такие катушки применяются для обеспечения индуктивной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току цепи базыиколлектораи т. д. К таким катушкам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи. Вариометры Это катушки, индуктивность которых можно изменять в процессе эксплуатации для перестройки колебательных контуров. Они состоят из двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая располагается внутри первой и вращается (ротор). При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника. Дроссели Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Обычно включаются в цепях питания усилительных устройств. Предназначены для защиты источников питания от попадания в них высокочастотных сигналов. На низких частотах они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Сдвоенный дроссель Сдвоенные дроссели две намотанных встречно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукцииболее эффективны при тех же габаритных размерах. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике. Катушки индуктивности (совместно с конденсаторамии/илирезисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепейобратной связи,колебательных контурови т. п.. Катушки индуктивности используются в импульсных стабилизаторахкак элемент, накапливающий энергию и преобразующий уровни напряжения. Две и более индуктивно связанные катушки образуют трансформатор. Катушка индуктивности, питаемая импульсным током от транзисторного ключа, иногда применяется в качестве источника высокого напряжения небольшой мощности в слаботочных схемах, когда создание отдельного высокого питающего напряжения в блоке питания невозможно или экономически нецелесообразно. В этом случае на катушке из-засамоиндукциивозникают выбросы высокого напряжения, которые можно использовать в схеме, например, выпрямив и сгладив. Катушки используются также в качестве электромагнитов. Катушки применяются в качестве источника энергии для возбуждения индуктивно-связанной плазмы. Для радиосвязи — излучение и приём электромагнитных волн (магнитная антенна, кольцевая антенна). Для разогрева электропроводящих материалов в индукционных печах. Как датчикперемещения: изменение индуктивности катушки может изменяться в широких пределах перемещением (вытаскиванием) сердечника. Катушка индуктивности используется в индукционных датчиках магнитного поля. Индукционные магнитометрыбыли разработаны и широко использовались во временаВторой мировой войны.[3] studfiles.net Рис. 4.12. Условное обозначение катушки индуктивности. Рис. 4.13 если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения. Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн). Постоянная времени RС-цепи На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания. Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е, называется постоянной времени контура или цепи. Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения. Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени. Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах. Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени. Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени. Постоянная времени RL-цепи Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно E/R = 20 В/1 кОм = 20 мА. Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи. Рис. 4.16. Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности. Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв. Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω= 2πf, где f – частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода). Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω= 2πf. Это означает, что угол между этими векторами Рис. 4.18. Векторное представление синусоидального сигнала. Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ (или вектор ОВ отстает от вектора ОА) на угол θ. изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени. Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока. В этом видео рассказывается о катушке индуктивности: Устройство и принцип работы катушки индуктивности. Напряжение на катушке
Катушка индуктивности - Практическая электроника
Устройство и принцип работы катушки индуктивности.
Устройство и принцип работы катушки индуктивности.
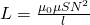
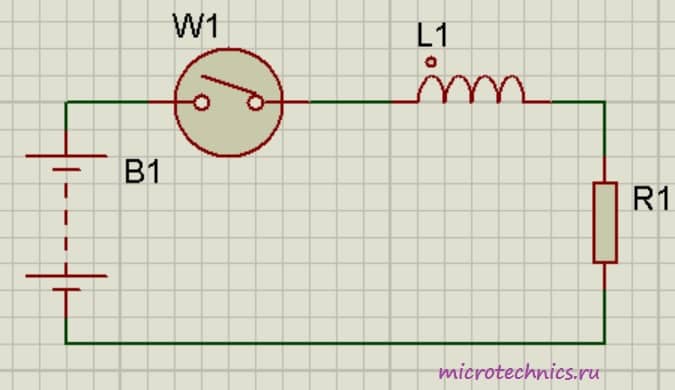
Катушка индуктивности в цепи постоянного тока.
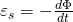
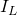будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
Катушка индуктивности в цепи переменного тока.
, 
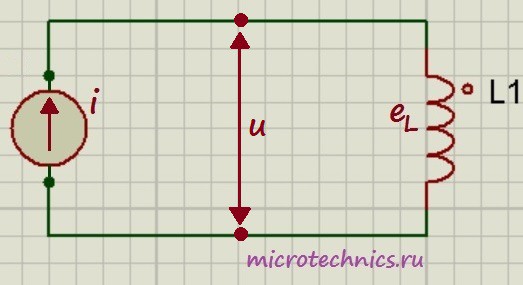
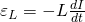
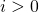, участок 3-4: 
, 
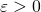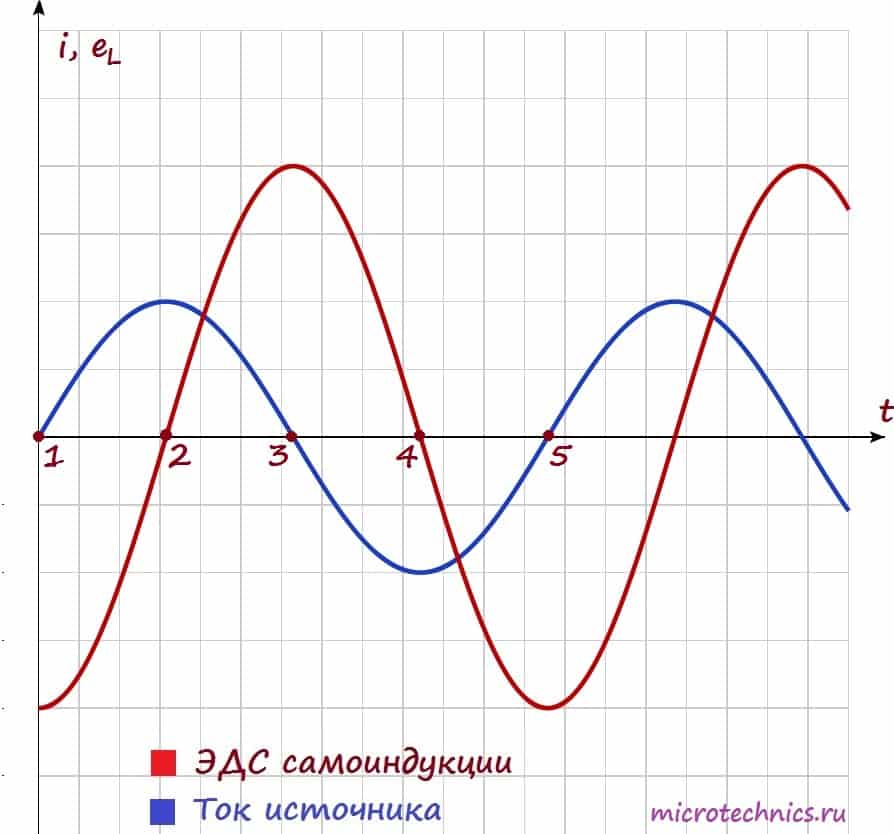
). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника). А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока). И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом: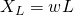
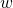– круговая частота: 
. 
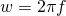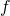– это частота переменного тока. 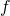= 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
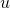? Здесь все на самом деле просто 🙂 По 2-му закону Кирхгофа: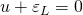
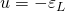
Катушка индуктивности в цепи постоянного и переменного тока
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
Катушка индуктивности
Устройство
Свойства катушки индуктивности
Характеристики катушки индуктивности
] Индуктивность
Основным параметром катушки индуктивности является её индуктивность, которая определяет, какой поток магнитного поля создаст катушка при протекании через неё тока силой 1 ампер. Типичные значения индуктивностей катушек от десятых долей мкГн до десятков Гн.
Индуктивность соленоида
Индуктивность торойда
Сопротивление потерь
Потери в проводах
Потери в диэлектрике
Потери в сердечнике
Потери в сердечнике складываются из потерь на вихревые токи, потерь на гистерезис и начальных потерь.
Потери в экране
Добротность
Температурный коэффициент индуктивности (ТКИ)
Разновидности катушек индуктивности
Применениекатушек индуктивности
Катушка индуктивности
Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,
Сопротивление по постоянному току
Векторное представление
Добавить комментарий
radiolubitel.net
Катушка индуктивности в цепи переменного тока
Если катушка индуктивности включена в цепь переменного тока, то в такой цепи, фаза тока всегда отстает от фазы напряжения. Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление, а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.
Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.
Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции
В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т. е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.
По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.
Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.
Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.
С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.
В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.
Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.
В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).
Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.
Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.
Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения. Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).
Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.
В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС, противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции, а скорость вагонетки — электрическому току. Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис. 1б), в точности соответствующие графикам рис.1а.
Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.
Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».
Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Для чего нужна катушка индуктивности
Стандартная конструкция катушки индуктивности состоит из изолированного провода с одной или несколькими жилами, намотанными в виде спирали на каркас из диэлектрика, имеющего прямоугольную, цилиндрическую или тороидальную форму. Иногда, конструкции катушек бывают бескаркасными. Наматывание провода производится в один или несколько слоев.
Для того, чтобы увеличить индуктивность, используются сердечники из ферромагнитов. Они же позволяют изменять индуктивность в определенных пределах. Не всем до конца понятно, для чего нужна катушка индуктивности. Ее используют в электрических цепях, как хороший проводник постоянного тока. Однако, при возникновении самоиндукции, возникает сопротивление, препятствующее прохождению переменного тока.
Разновидности катушек индуктивности
Существует несколько вариантов конструкций катушек индуктивности, свойства которых определяют и сферу их использования. Например, применение контурных катушек индуктивности вместе с конденсаторами, позволяют получать резонансные контуры. Они отличаются высокой стабильностью, качеством и точностью.
Катушки связи обеспечивают индуктивную связь отдельных цепей и каскадов. Таким образом, становится возможным деление базы и цепей по постоянному току. Здесь не требуется высокой точностью, поэтому, для этих катушек используется тонкий провод, наматываемый в две небольшие обмотки. Параметры данных приборов определяются в соответствии с индуктивностью и коэффициентом связи.
Некоторые катушки используются в качестве вариометров. Во время эксплуатации их индуктивность может изменяться, что позволяет успешно перестраивать колебательные контуры. Весь прибор включает в себя две последовательно соединенных катушки. Подвижная катушка вращается внутри неподвижной катушки, тем самым, создавая изменение индуктивности. Фактически, они являются статором и ротором. Если их положение изменится, то поменяется и значение самоиндукции. В результате, индуктивность прибора может измениться в 4-5 раз.
В виде дросселей используются те приборы, у которых при переменном токе отмечается высокое сопротивление, а при постоянном – очень низкое. Благодаря этому свойству, они используются в радиотехнических устройствах в качестве фильтрующих элементов. При частоте 50-60 герц для изготовления их сердечников применяется трансформаторная сталь. Если частота имеет более высокое значение, то сердечники изготавливаются из феррита или пермаллоя. Отдельные разновидности дросселей можно наблюдать в виде так называемых бочонков, подавляющих помехи на проводах.
Где применяются катушки индуктивности
Сфера применения каждого такого прибора, тесно связана с особенностями его конструкции. Поэтому нужно обязательно учитывать ее индивидуальные свойства и технические характеристики.
Совместно с резисторами или конденсаторами, катушки задействованы в различных цепях, имеющих частотно-зависимые свойства. Прежде всего, это фильтры, колебательные контуры, цепи обратной связи и прочее. Все виды этих приборов способствуют накоплению энергии, преобразованию уровней напряжения в импульсном стабилизаторе.
При индуктивной связи между собой двух и более катушек, происходит образование трансформатора. Эти приборы могут использоваться, как электромагниты, а также, как источник энергии, возбуждающий индуктивно связанную плазму.
Индуктивные катушки успешно используются в радиотехнике, в качестве излучателя и приемника в конструкциях кольцевых и магнитных антенн, работающих с электромагнитными волнами.
electric-220.ru
Поделиться с друзьями: