Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный[1]пробный заряд, помещенный в данную точку поля, к величине этого заряда : Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе). В каждой точке пространства в данный момент времени существует свое значение вектора (вообще говоря - разное[3] в разных точках пространства), таким образом, - это векторное поле. представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к. может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле[4], и законы, которым оно подчиняется, есть предмет электродинамики. Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон. Из сказанного выше ясно, что напряженность электрического поля - одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал). Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля. Полная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца: где q - электрический заряд частицы, - ее скорость, - вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ. Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, т.к. включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля. В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов - надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически - бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы. Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца, частными случаями ее применения итп. Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы. Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля: Здесь - плотность заряда, - плотность тока, - универсальные константы (уравнения здесь записаны в единицах СИ). Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла - так называемые "уравнения для вакуума" (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла - см. основную статью. Этих четырех уравнений вместе с пятым - уравнением силы Лоренца - в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют ее полные законы. Для решения конкретных реальных задач с их помощью необходимы еще уравнения движения "материальных частиц" (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом. Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности: Связь напряженности электрического поля с потенциалами в общем случае такова: где - скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции: В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до: Это выражение для связи электростатического поля с электростатическим потенциалом. Важным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел. Этим частным случаем занимается раздел электродинамики, называемый электростатикой. Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как или то есть электростатическое поле оказывается потенциальным полем. ( в этом случае - случае электростатики - принято называть электростатическим потенциалом). Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона: а в областях, свободных от заряженных частиц - к уравнению Лапласа: Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда). Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла: где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q - полный (суммарный) заряд внутри этой поверхности. Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости. Для точечного заряда в электростатике верен закона Кулона или Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: , имеем: откуда сразу получаем ответ для E. Ответ для получается тогда интегрированием E: Формулы и их вывод аналогичны, отличие от СИ лишь в константах. По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем: где каждое Подставив, получаем: Для непрерывного распределения аналогично: где V - область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, - радиус-вектор точки, для которой считаем , - радиус-вектор источника, пробегающий все точки области V при интегрировании, dV - элемент объема. Можно подставить x,y,z вместо , вместо , вместо dV. В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m). dic.academic.ru В пространстве вокруг электрически заряженного тела существует электрическое поле, представляющее собой один из видов материи. Электрическое поле обладает энергией, которая проявляется в виде сил, действующих на находящиеся в поле заряженные тела. Электрическое поле условно изображают в виде силовых линий, которые направлены в ту сторону, в которую двигалась бы в поле положительно заряженная частица. Напряженность поля. Электрическое поле действует на внесенный в него заряд q (рис. 4) с некоторой силой F. Следовательно, об интенсивности электрического поля можно судить по значению силы, с которой притягивается или отталкивается некоторый электрический заряд. В электротехнике интенсивность поля характеризуют напряженностью электрического поля Е, под которой понимают отношение силы F, действующей на заряженное тело в данной точке поля, к заряду q этого тела: E= F/q По мере удаления от заряженного тела силовые линии электрического поля располагаются реже, т. е. напряженность поля E уменьшается (рис. 3,а,б и в). Только в однородном электрическом поле (рис. 3,г) напряженность одинакова во всех его точках. Электрический потенциал. Электрическое поле обладает определенным запасом энергии, т. е. способностью совершать работу, которая может быть реализована, если внести в него какой-либо заряд. Этот заряд будет перемещаться по направлению силовых линий, совершая определенную работу. Для характеристики энергии, запасенной в каждой точке электрического поля, введено специальное понятие — электрический потенциал. Электрический потенциал φ поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля. За нулевой потенциал условно принимают потенциал, который имеет поверхность земли. Электрическое напряжение.Разные точки электрического поля обладают разными потенциалами. Обычно нас мало интересует абсолютная величина потенциалов отдельных точек электрического поля, важнее знать разность потенциалов φ1-φ2 между двумя точками поля А и Б (рис. 5). Разность потенциалов φ1 и φ2 двух точек поля характеризует собой работу, затрачиваемую силами поля на перемещение заряда из одной точки поля с большим потенциалом в другую - точку с меньшим потенциалом и носит название электрического напряжения. Электрическое напряжение обозначают буквой U. Единицей электрического напряжения служит Вольт (В). В веществе, помещенном в электрическое поле, возникает процесс направленного движения элементарных носителей электричества. Заряженными частицами являются электроны или ионы. Движение этих электрически заряженных частиц называется электрическим током. Единицей силы тока служит Ампер (А). Это такой ток, при котором через поперечное сечение проводника каждую секунду проходит количество электричества, равное 1 Кл. В формулах ток обозначают буквой I. В электротехнике широко применяют как постоянный, так и переменный ток. Постоянным называют ток, значение и направление которого в любой момент времени остаются неизменными (рис. 6, а). Токи, значение и направление которых не остаются постоянными, называют изменяющимися, или переменными. Свойство вещества проводить электрический ток под действием электрического поля называют электропроводностью. Электропроводность различных веществ зависит от концентрации свободных электрически заряженных частиц. Чем их больше, тем больше электропроводность данного вещества. Все вещества в зависимости от электропроводности делят на три группы: проводники, диэлектрики (изолирующие материалы) и полупроводники. Высокая электропроводность металлов объясняется электронной теорией строения атома, согласно которой атомы металлов имеют такое строение, при котором электроны на последней электронной орбите сравнительно слабо связаны с ядрами атомов. Поэтому они свободно перемещаются между атомами, переходя от одного к другому и заполняя пространство между ними. Эти электроны называются свободными. Если внести металлический проводник в электрическое поле, то свободные электроны под действием сил поля начнут перемещаться в сторону положительного полюса, создавая электрический ток. Таким образом, электрическим током в металлических проводниках называется упорядоченное (направленное) движение свободных электронов. studfiles.net Напряжённость электрического по́ля — векторная характеристика электрического поля в данной точке, равная отношению силы , действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q: По сути, задает само векторное поле, поскольку его величина и направление меняется в пространстве от точки к точке. Используя потенциал Вектор выражается как градиент потенциала, взятый с обратным знаком: . К примеру, для точечного заряда, исходя из закона Кулона . Так как эквипотенциальные поверхности являются в этом случае сферами, то производная по нормали есть производная по радиусу. Таким образом мы можем прийти к так называемому кулоновскому полю:; Используя теорему Остроградского — Гаусса Из формулы Остроградского-Гаусса вектор можно определить, зная плотность распределения зарядов. Согласно Формуле О-Г, а также используя уравнение Максвелла , легко получить: где qin — заряд, находящийся внутри замкнутой поверхности S, объемом V. В качестве поверхности интегрирования возьмем сферу (центральная симметрия), тогда И самоочевидно: Как и следовало ожидать, результаты полностью совпали. Рассуждения аналогичны, вся разница лишь в том, что изменяется вид потенциала , уравнение Максвелла и . В итоге, получаем в системе СГС: В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в Ньютонах на Кулон или в Вольтах на метр (В/м или V/m). Wikimedia Foundation. 2010. dic.academic.ru Главное свойство электрического поля – способность действовать на электрические заряды с некоторой силой, поэтому естественно охарактеризовать электрическое поле с помощью силы, действующей на точечный положительный заряд, внесенный в это поле. Напряженностью электрического поля в данной точке называют физическую величину, численно равную силе, действующей на единичный положительный заряд, помещенный в данную точку и имеющей направление этой силы: . (6.2) В частности, напряженность в любой точке поля, созданного точечным зарядом (как это следует из закона Кулона), равна . (6.3) Напряженность поля не зависит от величины пробного заряда, а определяется величиной и знаком заряда, создающего поле, и положением (координатой) выбранной точки поля. Напряженность поля определяет величину и направление силы, действующей на заряд, помещенный в данную точку поля: (6.4) Если поле создано двумя или несколькими зарядами, то электрическое поле каждого заряда (как утверждает опыт) не зависит друг от друга, и напряженность электрического поля, поэтому определяется как векторная сумма напряженностей полей, создаваемых отдельными зарядами (рис. 6.1). В этом состоит принцип суперпозиции полей: . (*) Для наглядного (графического) описания электрических полей используется понятие силовой линии поля. Силовой линией называют линию, проведенную в электрическом поле так (рис. 6.2), чтобы касательная в любой ее точке совпадала с направлением вектора напряженности. Силовой линии приписывают направление, совпадающее с направлением вектора напряженности в каждой ее точке. Так как каждой точке поля соответствует вполне определенный вектор напряженности поля, то силовые линии нигде не пересекаются. Условились при изображении электрических полей с помощью линий напряженности, число силовых линий, проходящих через единичную поверхность, перпендикулярную к силовым линиям в данной точке поля, выбирать равным напряженности поля Е в данной точке (в этом состоит правило графического изображения полей с помощью силовых линий). При таком условии картина силовых линий электрического поля позволяет наглядно судить как о направлении, так и о величине напряженности поля в каждой точке. Помимо напряженности электрическое поле характеризуется еще одной важной физической величиной – потенциалом. Рассмотрим перемещение заряда q в поле другого точечного заряда q0 из точки 1 в точку 2 (рис. 6.3). Работа силы F на элементарном перемещении dl определяется соотношением , (6.5) но , значит. Подставим сюда вместо силы ее значение из закона Кулона, получим: . (6.6) Для вычисления работы перемещения заряда из точки 1 в точку 2 по произвольному пути 1–2 проинтегрируем (6.6) в пределах от r1 до r2 , получим . (6.7) Из выражения (6.7) следует, что работа перемещения электрического заряда не зависит от формы пути, по которому перемещается заряд, а зависит только от начальной и конечной точек. Если заряд q, перемещаясь в электрическом поле, возвращается в исходную точку (r2 = r1), то работа перемещения заряда по замкнутому пути в электростатическом поле равна нулю. Поля, обладающие указанным свойством, называются потенциальными. Найдем отношение работы перемещения заряда к величине этого заряда: . (6.8) Эта величина не зависит от величины перемещаемого заряда и от пути, по которому он перемещается, и поэтому служит характеристикой поля, созданного зарядом q0 , и называется разностью потенциалов или электрическим напряжением. Разность потенциалов двух точек 1 и 2 электрического поля измеряется работой, совершаемой полем при перемещении единичного положительного заряда между этими точками. Следует подчеркнуть, что разность потенциалов имеет смысл характеристики поля потому, что работа перемещения заряда не зависит от формы пути. Действительно, если бы работа перемещения заряда зависела от пути, то при перемещении одного и того же заряда между теми же самыми точками поля, это отношение A / q не являлось бы однозначной характеристикой этих точек поля. Если выбрать какую-либо точку пространства в качестве начальной точки (точки отсчета), то любой точке можно сопоставить разность потенциалов относительно этой начальной точки. Для случая поля точечного заряда наиболее простое математическое выражение для потенциала получается, если в качестве начальной выбрать любую точку, удаленную на бесконечность. Тогда работа перемещения положительного заряда q из бесконечности в данную точку поля, созданного другим точечным зарядом q0 , будет равна . (6.9) Отношение работы перемещения положительного заряда из бесконечности в данную точку поля к величине этого заряда (работа по перемещению единичного заряда) называется потенциалом данной точки поля: . (6.10) Знак минус в этом выражении означает, что в данном случае работа совершается внешними силами против сил поля. Очевидно, что напряжение U между произвольными точками 1 и 2 электрического поля и потенциалы этих точек связаны простым соотношением . (6.11) Для поля точечного заряда . (6.12) Потенциал любой точки поля, созданного положительным зарядом – положителен и убывает до нуля по мере удаления от заряда. Напротив – потенциал поля, созданного отрицательным зарядом, – отрицательная величина и растет до нуля по мере удаления от заряда. Из выражения для потенциала (6.12) следует, что потенциал любой точки сферической поверхностиS c центром в точке расположения заряда одинаков (рис. 6.4). Такие поверхности называются поверхностями равного потенциала или эквипотенциальными поверхностями. Работу перемещения заряда можно выразить через разность потенциалов . (6.13) Отсюда следует, что работа перемещения заряда по эквипотенциальной поверхности равна нулю. Это значит, что сила, действующая на заряд, а следовательно, и вектор напряженности поля Е направлены перпендикулярно эквипотенциальной поверхности. Используя эквипотенциальные поверхности, можно также дать графическое изображение электрического поля. Результаты, полученные для поля точечного заряда, легко распространить на поля, созданные любым числом точечных зарядов, а так как любое заряженное тело можно представить как совокупность точечных зарядов, то и на поле, созданное любым заряженным телом. Поля точечных зарядов в соответствии с принципом суперпозиции, накладываясь друг на друга, не влияют друг на друга. Поэтому потенциал поля любого числа зарядов будет равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, т. е.: . (6.14) Таким образом, все вышеизложенное в отношении понятия потенциала справедливо и для поля, созданного заряженным телом любой формы, а величину потенциала, в принципе, можно вычислить по формуле (6.14). studfiles.net Напряженность поля (Е) - характеризует интенсивность электрического поля, т.е. его способность притягивать или отталкивать некоторый электрический заряд принятый за единицу. Электрический потенциал (φ) характеризует энергию, запасенную в каждой точке поля. Электрический потенциал поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля. За нулевой потенциал условно принят потенциал поверхности земли. Разность потенциалов двух точек поля характеризует собой работу, затрачиваемую силами поля на перемещение единичного положительного заряда из одной точки поля с большим потенциалом в другую точку с меньшим потенциалом, и называется электрическим напряжением (U)U=φ1- φ2 [В] Электрический ток и электропроводность вещества. Согласно электронной теории одни атомы могут терять электроны, другие же приобретать их, в результате чего превращаются в положительные и отрицательные ионы. Этот процесс называется ионизацией. Ионизация может возникнуть только при сообщении атому определенного количества энергии: в виде тепла, облучения и т.д. Электроны, потерявшие связь с атомами и перемещающиеся в пространстве между ними, называются свободными. Если в каком-либо теле накопятся электроны или ионы, то говорят, что в теле накопилось электричество или они несут электрический заряд. Единицей электрического заряда принято считать заряд электрона. В системе СИ количество электричества измеряют в кулонах 1Кл=6,29*1018 электронов. В веществе, помещенном в электрическое поле, под действием сил поля возникает процесс движения элементарных носителей электричества – ионов и электронов. Направленное движение электрически заряженных частиц под действием электрического поля называется электрическим током (I). За единицу силы тока принят ампер [A]: это такой ток, при котором через поперечное сечение проводника каждую секунду проходит 1 кулон электричества. Постоянным называется ток, значение и направление которого в любой момент времени остаются неизменными. Токи, значение и (или) направление которых не остаются постоянными, называются переменными. Свойство вещества проводить электрический ток под действием электрического поля называется электропроводностью. Электропроводность веществ зависит от концентрации свободных электрически заряженных частиц. Все вещества в зависимости от электропроводности делятся на проводники, полупроводники и диэлектрики. Существует два рода проводников, которые различаются физической природой протекания электрического тока. Это металлы – ток в них обусловлен движением свободных электронов (электронная проводимость) и электролиты – прохождение тока в них связано с движением ионов (ионная проводимость). Электрическое сопротивление и проводимость. При движении свободных электронов в проводнике они сталкиваются с ионами и атомами вещества, из которого сделан проводник и передают им часть своей энергии, которая выделяется в виде тепла, нагревающего проводник. Противодействие проводника прохождению электрического тока называется электрическим сопротивлением (R) [Ом]. Сопротивление прямолинейного проводника зависит не только от материала проводника, но и его длины и площади поперечного сечения. R= ρl/s; ρ [Ом/м/мм2] Электрическая цепь Электрическую цепь можно разделить на два участка: внутреннюю цепь (сам источник) и внешнюю цепь (линейные провода и приемники). Чертеж, на котором на котором изображены электрические цепи с помощью условных графических обозначений, называют электрической схемой (Рис.11). Во внешней цепи ток направлен от плюса к минусу, внутри источника наоборот. Такое перемещение зарядов внутри источника совершается благодаря э.д.с., которая возбуждается внутри источника. Э.д.с. поддерживает разность потенциалов на зажимах источника и определяет собой напряжение источника питания. Э.д.с. обозначается Е и численно, равна работе, которую необходимо затратить на перемещение единичного положительного заряда от одного зажима к другому. Направления тока, напряжения и э.д.с. на схемах изображают стрелками, за положительное направление тока принимают движение положительных зарядов, т.е. от плюса к минусу. Положительное направление напряжения и э.д.с. совпадает с направлением тока. Закон Ома для электрической цепи: сила тока в электрической цепи равна э.д.с. источника поделенного на полное сопротивление цепи, которое можно представить виде суммы сопротивления приемника и внутреннего сопротивления источника питания. I=E/R I=E/R+R0 Закон Омаможет быть применен не ко всей цепи, но к любому ее участку (например аб): сила тока на данном участке цепи равна напряжению, приложенному к участку, поделенному на сопротивление этого участка. I=U/R; U=IR; R=U/I Закон Ома применим только к линейным цепям. Способы соединения потребителей. При последовательном соединении (рис.12)по всем элементам цепи протекает один и тот же ток. E=IR1+IR2 = I(R1+R2)=IRЭ. Если последовательно включеноnрезисторов с одинаковыми сопротивлениями R, то RЭ=nR При параллельном соединении (рис.13) нескольких приемников ко всем резисторам приложено одинаковое напряжение I=U/R1+U/R2 =U/(1/R1+1/R2) Для двух резисторов При параллельном включении n одинаковых резисторов RЭ= R/n. При смешанном соединении резисторовэквивалентное сопротивление определяют методом преобразования. Понятие о магнитном поле При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю. Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Интенсивность магнитного поля, т.е. его способность производить работу определяется магнитной индукцией (В). Магнитный поток (Ф), проходящий через какую-либо поверхность, определяется общим числом м.с.л. пронизывающих эту поверхность Ф=BS, B=Ф/S, где S поперечное сечение магнитопровода. Магнитная индукция зависит не только от тока, возбуждающего магнитное поле, но и от среды, в которой оно существует. Влияние среды на магнитное поле характеризуется абсолютной магнитной проницаемостью среды µа (Гн/м) Относительная магнитная проницаемость µотн=µа/µ0, где µ0-магнитная проницаемость вакуума = 4π*10-7(Гн/м). Напряженность магнитного поля Н не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводника на интенсивность магнитного поля в данной точке. H=B/µа (А/м) cyberpedia.su Заряженное тело постоянно передает часть энергии, преобразуя ее в другое состояние, одной из частей которого является электрическое поле. Напряженность – основная составляющая, которая характеризует электрическую часть электромагнитного излучения. Его значение зависит от силы тока и выступает силовой характеристикой. Именно по этой причине высоковольтные провода размещают на большую высоту, чем проводку для меньшего тока. Вектор напряженности (E) — сила, действующая на бесконечно малый ток в рассматриваемой точке. Формула для определения параметра выглядит следующим образом: Где: Заряд, принимающий участие в исследовании, называется пробным. Он должен быть незначительным, чтобы не искажать результаты. При идеальных условиях в роли q выступает позитрон. Стоит отметить, что величина относительна, ее количественная характеристика и направление зависят от координат и при смещении изменится. Исходя из закона кулона сила, действующая на тело, равняется произведению потенциалов, деленному на квадрат расстояния между телами. F=q1*q2/r2 Из этого следует, что напряженность в данной точке пространства прямо пропорциональна потенциалу источника и обратно пропорциональна квадрату расстояния между ними. В общем, символическом случае уравнение записывается следующим образом: E=q/r2 Исходя из уравнения, единица измерения электрического поля – Вольт на метр. Это же обозначение принято системой СИ. Имея значение параметра, можно вычислить силу, которая будет действовать на тело в исследуемой точке, а зная силу — найти напряженность электрического поля. По формуле видно, что результат абсолютно не зависит от пробного заряда. Это необычно, так как данный параметр присутствует в первоначальном уравнении. Однако это логично, потому что источником является основной, а не пробный излучатель. В реальных условиях данный параметр имеет влияние на измеряемые характеристики и выдает искажение, что обуславливает использование позитрона для идеальных условий. Так как напряженность – векторная величина, кроме значения она имеет направление. Вектор направлен от основного источника к исследуемому, или от пробного заряда к основному. Это зависит от полярности. Если знаки одинаковые, то происходит отталкивание, вектор направлен к исследуемой точке. Если точки заряжены разнополярно, то источники притягиваются. В этом случае принято считать, что вектор силы направлен от положительного источника к отрицательному. В зависимости от контекста и применения в областях электростатики напряженность электрического поля [E] измеряется в двух единицах. Это могут быть вольт/метр или ньютон/кулон. Причиной такой путаницы представляется получение ее из разных условий, выведение единицы измерений из применяемых формул. В некоторых случаях одна из размерностей используется намерено для предотвращения применения формул, которые работают только для частных случаев. Понятие присутствует в фундаментальных электродинамических законах, поэтому величина является для термодинамики базовой. Источник может принимать различные формы. Описанные выше формулы помогают найти напряженность электрического поля точечного заряда, но источник может представлять собой и другие формы: Для точечного заряда нахождение напряженности выглядит следующим образом: E=k*q/r2, где k=9*109 При воздействии на тело нескольких источников напряженность в точке будет равняться векторной сумме потенциалов. При действии распределенного источника вычисляется действующим интегралом по всей области распределения. Характеристика может изменяться во времени в связи с изменением зарядов. Значение остается постоянным только для электростатического поля. Она является одной из основных силовых характеристик, поэтому для однородного поля направление вектора и величина q будут одинаковыми в любых координатах. Напряженность выступает одним из основных и ключевых характеристик в классической электродинамике. Ее значение, а также данные электрического заряда и магнитной индукции представляются основными характеристиками, зная которые можно определить параметры протекания практически всех электродинамических процессов. Она присутствуют и выполняет важную роль в таких фундаментальных понятиях, как формула силы Лоренца и уравнения Максвелла. Где: F-сила Лоуренца; Наряду со значением магнитной индукцией данный параметр является основной характеристикой электромагнитного поля, излучаемого зарядом. Исходя из этого, с точки зрения термодинамики напряженность – значительно более важное значение, чем сила тока или другие показатели. Данные законы выступают фундаментальными, на них строится вся термодинамика. Следует отметить, что закон Ампера и другие более ранние формулы являются приближенными или описывают частные случаи. Законы Максвелла и Лоренца универсальны. Понятие напряженности нашло широкое применение в электротехнике. Оно применяется для расчетов норм сигналов, вычисления устойчивости системы, определения влияния электрического излучения на окружающие источник элементы. Основной сферой, где понятие нашло широкое применение, является сотовая и спутниковая связь, телевышки и другие электромагнитные излучатели. Знание интенсивности излучения для данных устройств позволяют рассчитать такие параметры, как: Первый параметр крайне важен для тех, кто устанавливает спутниковое телевизионное вещание, а также мобильную связь. Второй дает возможность определить допустимые нормы по излучению, тем самым обезопасив пользователей от вредного влияния электроприборов. Применение данных свойств электромагнитного излучения не ограничивается связью. На этих базовых принципах построена выработка энергии, бытовая техника, отчасти производство механических изделий (например, окрашивание при помощи электромагнитных импульсов). Таким образом, понимание величины является важным и для производственного процесса. Интересные опыты, позволяющие увидеть картину силовых линий электрического поля: видео Читайте также: electroadvice.ru Напряженность поля (Е) - характеризует интенсивность электрического поля, т.е. его способность притягивать или отталкивать некоторый электрический заряд принятый за единицу. Электрический потенциал (φ) характеризует энергию, запасенную в каждой точке поля. Электрический потенциал поля в данной точке равен работе, которую могут совершить силы этого поля при перемещении единицы положительного заряда из этой точки за пределы поля. За нулевой потенциал условно принят потенциал поверхности земли. Разность потенциалов двух точек поля характеризует собой работу, затрачиваемую силами поля на перемещение единичного положительного заряда из одной точки поля с большим потенциалом в другую точку с меньшим потенциалом, и называется электрическим напряжением (U)U=φ1- φ2 [В] Электрический ток и электропроводность вещества. Согласно электронной теории одни атомы могут терять электроны, другие же приобретать их, в результате чего превращаются в положительные и отрицательные ионы. Этот процесс называется ионизацией. Ионизация может возникнуть только при сообщении атому определенного количества энергии: в виде тепла, облучения и т.д. Электроны, потерявшие связь с атомами и перемещающиеся в пространстве между ними, называются свободными. Если в каком-либо теле накопятся электроны или ионы, то говорят, что в теле накопилось электричество или они несут электрический заряд. Единицей электрического заряда принято считать заряд электрона. В системе СИ количество электричества измеряют в кулонах 1Кл=6,29*1018 электронов. В веществе, помещенном в электрическое поле, под действием сил поля возникает процесс движения элементарных носителей электричества – ионов и электронов. Направленное движение электрически заряженных частиц под действием электрического поля называется электрическим током (I). За единицу силы тока принят ампер [A]: это такой ток, при котором через поперечное сечение проводника каждую секунду проходит 1 кулон электричества. Постоянным называется ток, значение и направление которого в любой момент времени остаются неизменными. Токи, значение и (или) направление которых не остаются постоянными, называются переменными. Свойство вещества проводить электрический ток под действием электрического поля называется электропроводностью. Электропроводность веществ зависит от концентрации свободных электрически заряженных частиц. Все вещества в зависимости от электропроводности делятся на проводники, полупроводники и диэлектрики. Существует два рода проводников, которые различаются физической природой протекания электрического тока. Это металлы – ток в них обусловлен движением свободных электронов (электронная проводимость) и электролиты – прохождение тока в них связано с движением ионов (ионная проводимость). Электрическое сопротивление и проводимость. При движении свободных электронов в проводнике они сталкиваются с ионами и атомами вещества, из которого сделан проводник и передают им часть своей энергии, которая выделяется в виде тепла, нагревающего проводник. Противодействие проводника прохождению электрического тока называется электрическим сопротивлением (R) [Ом]. Сопротивление прямолинейного проводника зависит не только от материала проводника, но и его длины и площади поперечного сечения. R= ρl/s; ρ [Ом/м/мм2] Электрическая цепь Электрическую цепь можно разделить на два участка: внутреннюю цепь (сам источник) и внешнюю цепь (линейные провода и приемники). Чертеж, на котором на котором изображены электрические цепи с помощью условных графических обозначений, называют электрической схемой (Рис.11). Во внешней цепи ток направлен от плюса к минусу, внутри источника наоборот. Такое перемещение зарядов внутри источника совершается благодаря э.д.с., которая возбуждается внутри источника. Э.д.с. поддерживает разность потенциалов на зажимах источника и определяет собой напряжение источника питания. Э.д.с. обозначается Е и численно, равна работе, которую необходимо затратить на перемещение единичного положительного заряда от одного зажима к другому. Направления тока, напряжения и э.д.с. на схемах изображают стрелками, за положительное направление тока принимают движение положительных зарядов, т.е. от плюса к минусу. Положительное направление напряжения и э.д.с. совпадает с направлением тока. Закон Ома для электрической цепи: сила тока в электрической цепи равна э.д.с. источника поделенного на полное сопротивление цепи, которое можно представить виде суммы сопротивления приемника и внутреннего сопротивления источника питания. I=E/R I=E/R+R0 Закон Омаможет быть применен не ко всей цепи, но к любому ее участку (например аб): сила тока на данном участке цепи равна напряжению, приложенному к участку, поделенному на сопротивление этого участка. I=U/R; U=IR; R=U/I Закон Ома применим только к линейным цепям. Способы соединения потребителей. При последовательном соединении (рис.12)по всем элементам цепи протекает один и тот же ток. E=IR1+IR2 = I(R1+R2)=IRЭ. Если последовательно включеноnрезисторов с одинаковыми сопротивлениями R, то RЭ=nR При параллельном соединении (рис.13) нескольких приемников ко всем резисторам приложено одинаковое напряжение I=U/R1+U/R2 =U/(1/R1+1/R2) Для двух резисторов При параллельном включении n одинаковых резисторов RЭ= R/n. При смешанном соединении резисторовэквивалентное сопротивление определяют методом преобразования. Электрическое поле. Напряженность электрического поля, электрический потенциал и напряжение. Напряжение электрического поля это
Напряжённость электрического поля - это... Что такое Напряжённость электрического поля?
Напряжённость электрического поля в классической электродинамике
Сила, с которой действует электромагнитное поле на заряженные частицы
Уравнения Максвелла
«Материальные уравнения»
Связь с потенциалами
Электростатика
Теорема Гаусса
Напряжённость электрического поля точечного заряда
В единицах СИ
Для системы СГС
Напряженность электрического поля произвольного распределения зарядов
Системы единиц
Литература
Примечания
См. также
2. Электрическое поле. Напряженность поля, электрический потенциал и напряжение.
3. Электрический ток и электропроводность вещества.
Напряженность электрического поля - это... Что такое Напряженность электрического поля?
Напряжённость электрического поля точечного заряда
Для системы СИ
Для системы СГС
Системы единиц
См. также
Напряженность электрического поля
Потенциал электрического поля
Электрическое поле. Напряженность электрического поля, электрический потенциал и напряжение.

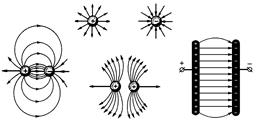 В пространстве вокруг заряженного тела существует электрическое поле, обладающее запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные частицы. Условно электрическое поле изображают в виде электрических силовых линий, которые показывают направление действия электрических сил, создаваемых полем (рис.10). Принято направлять силовые линии в ту сторону, в которую бы двигалась в поле положительно заряженная частица.
В пространстве вокруг заряженного тела существует электрическое поле, обладающее запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные частицы. Условно электрическое поле изображают в виде электрических силовых линий, которые показывают направление действия электрических сил, создаваемых полем (рис.10). Принято направлять силовые линии в ту сторону, в которую бы двигалась в поле положительно заряженная частица.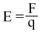 Численно напряженность поля определяется как отношение силы, действующей на заряженное тело, к заряду этого тела.
Численно напряженность поля определяется как отношение силы, действующей на заряженное тело, к заряду этого тела.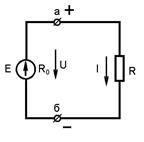 Электрическую цепь образуют источники электрической энергии (источники питания), ее приемники (электродвигатели, электронагревательные приборы, лампы) и соединительные провода, а также вспомогательное оборудование (для включения и выключения электроустановок), электроизмерительные приборы, защитные устройства.
Электрическую цепь образуют источники электрической энергии (источники питания), ее приемники (электродвигатели, электронагревательные приборы, лампы) и соединительные провода, а также вспомогательное оборудование (для включения и выключения электроустановок), электроизмерительные приборы, защитные устройства.
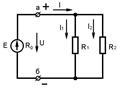
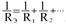 I=I1+I2+…
I=I1+I2+… I1:I2 =1/R1+1/R2
I1:I2 =1/R1+1/R2 формула, в чем измеряется, как найти.

Определение понятия и формула расчета



Единица измерения
Принцип суперпозиции

С точки зрения термодинамики


Практическое значение
Электрическое поле. Напряженность электрического поля, электрический потенциал и напряжение.

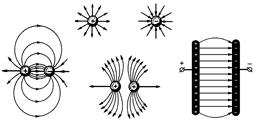 В пространстве вокруг заряженного тела существует электрическое поле, обладающее запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные частицы. Условно электрическое поле изображают в виде электрических силовых линий, которые показывают направление действия электрических сил, создаваемых полем (рис.10). Принято направлять силовые линии в ту сторону, в которую бы двигалась в поле положительно заряженная частица.
В пространстве вокруг заряженного тела существует электрическое поле, обладающее запасом электрической энергии, которая проявляется в виде электрических сил, действующих на находящиеся в поле заряженные частицы. Условно электрическое поле изображают в виде электрических силовых линий, которые показывают направление действия электрических сил, создаваемых полем (рис.10). Принято направлять силовые линии в ту сторону, в которую бы двигалась в поле положительно заряженная частица.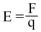 Численно напряженность поля определяется как отношение силы, действующей на заряженное тело, к заряду этого тела.
Численно напряженность поля определяется как отношение силы, действующей на заряженное тело, к заряду этого тела.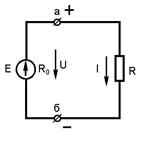 Электрическую цепь образуют источники электрической энергии (источники питания), ее приемники (электродвигатели, электронагревательные приборы, лампы) и соединительные провода, а также вспомогательное оборудование (для включения и выключения электроустановок), электроизмерительные приборы, защитные устройства.
Электрическую цепь образуют источники электрической энергии (источники питания), ее приемники (электродвигатели, электронагревательные приборы, лампы) и соединительные провода, а также вспомогательное оборудование (для включения и выключения электроустановок), электроизмерительные приборы, защитные устройства.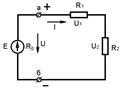

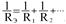 I=I1+I2+…
I=I1+I2+…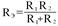 I1:I2 =1/R1+1/R2
I1:I2 =1/R1+1/R2
Похожие статьи:
poznayka.org








.jpg)


Поделиться с друзьями: