Формула напряжённости электрического поля. Напряжение через заряд

Напряженность поля точечного заряда | Объединение учителей Санкт-Петербурга

Напряженность поля точечного заряда.
Обозначим: q - заряд, создающий поле, q0 - заряд, помещенный в поле (внешний заряд). Закон Кулона: . Напряженность поля: . Тогда напряженность поля точечного заряда:
Теорема Гаусса. Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.
Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур.
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью.
Применения теоремы Гаусса.
1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности. А) Внутри сферы заряда нет . Е=0
Б) Снаружи сферы.
На поверхности сферы:
2. Напряженность поля шара заряженного по объему.
Введем понятие объемной плотности заряда: Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела. Объем шара произвольного радиуса . Обозначим q - заряд шара, q0 - заряд, находящийся внутри объема произвольного радиуса.
Тогда заряд сферы радиуса r , будет: Следовательно: . – напряженность поля внутри шара, равномерно заряженного по объему. Снаружи - см. 1.
3. Напряженность поля бесконечной заряженной плоскости.
Введем понятие поверхностной плотности заряда: . Тогда . Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S. Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости. 4. Напряженность поля плоского воздушного конденсатора. Из рисунка видим, что снаружи конденсатора поля пластин взаимно скомпенсированы, и общее поле равно нулю. Внутри конденсатора поля складываются. Используя вывод п.3 получаем: . Формула справедлива при условии, что расстояние между пластинами много меньше размеров самих пластин и вдали от краев пластин.

www.eduspb.com

Основные законы и формулы

ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Закон Кулона:

где F – сила взаимодействия двух точечных зарядов q1 и q2; r – расстояние между зарядами;  - диэлектрическая проницаемость среды; 0 - электрическая постоянная

Закон сохранения заряда:

где – алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.

Напряженность и потенциал электростатического поля:

; , или,

где – сила, действующая на точечный положительный зарядq0, помещенный в данную точку поля; П – потенциальная энергия заряда; А∞ - работа, затраченная на перемещение заряда q0 из данной точки поля в бесконечность.

Поток вектора напряженности электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле:

, или ,

где  – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; En – проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле:

Поток вектора напряженности через замкнутую поверхность –

(интегрирование ведется по всей поверхности).

Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –

где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.

Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –

Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:

внутри сферы (r R) Е=0;

на поверхности сферы (r=R) ;

вне сферы (r  R) .

Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой

В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет

где  - угол между векторами и.

Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –

где  - линейная плотность заряда.

Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):

Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –

где  - поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:

Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –

Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.

Электрическое смещение связано с напряженностьюэлектрического поля соотношением

которое справедливо только для изотропных диэлектриков.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:

Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:

Потенциал электрического поля в бесконечности условно принят равным нулю.

Потенциал электрического поля, создаваемый точечным зарядом q на

расстоянии r от заряда, –

Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:

внутри сферы (r  R) ;

на поверхности сферы (r = R) ;

вне сферы (r  R) .

Во всех формулах, приведенных для потенциала заряженной сферы,  есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.

Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов , создаваемых отдельными точечными зарядами:

Энергия W взаимодействия системы точечных зарядов определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой

где - потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд .

Потенциал связан с напряженностью электрического поля соотношением

В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

или в скалярной форме

В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –

где 1 и 2 – потенциалы точек двух эквипотенциальных поверхностей; d - расстояние между этими поверхностями вдоль электрической силовой линии.

Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал 1, в другую, имеющую потенциал 2, равна

, или ,

где E – проекция вектора на направление перемещения;- перемещение.

В случае однородного поля последняя формула принимает вид

где – перемещение; - угол между направлениями вектора и перемеще-ния.

Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.

Электрический момент диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению зарядана вектор, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.

Диполь называется точечным, если его плечо намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя ( r), см. рис. 1.

Рис. 1

Напряженность поля точечного диполя:

где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует;  - угол между радиус-вектором и плечомдиполя.

Напряженность поля точечного диполя в точке, лежащей на оси диполя

(=0), находится по формуле

;

в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , – по формуле

Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет

а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , –

=0.

Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.

Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –

, или ,

где  - угол между направлениями векторов и.

Электроемкость уединенного проводника или конденсатора –

где q – заряд, сообщенный проводнику; - изменение потенциала, вызванное этим зарядом.

Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –

Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.

Электроемкость плоского конденсатора:

где S – площадь каждой пластины конденсатора; d – расстояние между пластинами;  - диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной di и диэлектрической проницаемостью i каждый (слоистый конденсатор), составляет

Электроемкость сферического конденсатора (две концентрические сферы радиусом R1 и R2 , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:

Электроемкость последовательно соединенных конденсаторов составляет:

в общем случае –

где n – число конденсаторов;

в случае двух конденсаторов –

;

в случае n одинаковых конденсаторов с электроемкостью С1 каждый –

Электроемкость параллельно соединенных конденсаторов определяется следующим образом:

в общем случае –

С=С1+С2+…+Сn;

в случае двух конденсаторов –

С= С1+С2;

в случае n одинаковых конденсаторов с электроемкостью С1 каждый –

С=nС1.

Энергия заряженного проводника выражается через заряд q, потенциал  и электроемкость С проводника следующим образом:

Энергия заряженного конденсатора –

где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.

studfiles.net

Электрический заряд

Электрический заряд– физическая величина, характеризующая способность тел вступать в электромагнитные взаимодействия. Измеряется в Кулонах.

Элементарный электрический заряд– минимальный заряд, который имеют элементарные частицы (заряд протона и электрона).

e=Кл

Тело имеет заряд, значит имеет лишние или недостающий электроны. Такой заряд обозначаетсяq=ne. (он равен числу элементарных зарядов).

Наэлектризовать тело– создать избыток и недостаток электронов. Способы:электризация трениемиэлектризация соприкосновением.

Точечный заряд – заряд тела, которое можно принять за материальную точку.

Пробный заряд() – точечный, малый по величине заряд, обязательно положительный – используется для исследования электрического поля.

Закон сохранения заряда:в изолированной системе алгебраическая сумма зарядов всех тел сохраняется постоянной при любых взаимодействиях этих тел между собой.

Закон Кулона:силы взаимодействия двух точечных зарядов пропорциональны произведению этих зарядов, обратно пропорциональны квадрату расстояния между ними, зависят от свойств среды и направлены вдоль прямой, соединяющей их центры.

, гдеФ/м, Кл2/нм2– диэлектр. пост. вакуума

- относит. диэлектрическая проницаемость (>1)

- абсолютная диэлектрическая прониц. среды

Электрическое поле– материальная среда, через которую происходит взаимодействие электрических зарядов.

Свойства электрического поля:

Электрическое поле существует вокруг любого заряда. Если заряд неподвижен – поле электростатическое.
Электрическое поле действует на любой помещённый в него заряд согласно закону Кулона. Обнаружить электрическое поле можно только по его действию на другие заряды.
Электрическое поле существует в любой среде и распространяется с конечной скоростью: м/с.
Электрическое поле не имеет чётких границ. Действие его уменьшается при увеличении расстояния от заряда, его создающего.

Характеристики электрического поля:

Напряжённость(E) – векторная величина, равная силе, действующей на единичный пробный заряд, помещённый в данную точку.

Измеряется в Н/Кл.

Направление – такое же, как и у действующей силы.

Напряжённость не зависитни от силы, ни от величины пробного заряда.

Суперпозиция электрических полей: напряжённость поля, созданного несколькими зарядами, равна векторной сумме напряжённостей полей каждого заряда:

Графическиэлектронное поле изображают с помощью линий напряжённости.

Линия напряжённости– линия, касательная к которой в каждой точке совпадает с направлением вектора напряжённости.

Свойства линий напряжённости: они не пересекаются, через каждую точку можно провести лишь одну линию; они не замкнуты, выходят из положительного заряда и входят в отрицательный, либо рассеиваются в бесконечность.

Виды полей:

Однородное электрическое поле– поле, вектор напряжённости которого в каждой точке одинаков по модулю и направлению.

+ -

Неоднородное электрическое поле– поле, вектор напряжённости которого в каждой точке неодинаков по модулю и направлению.

Постоянное электрическое поле– вектор напряжённости не изменяется.
Непостоянное электрическое поле– вектор напряжённости изменяется.

Работа электрического поля по перемещению заряда.

, гдеF– сила,S– перемещение,- угол междуFиS.

Для однородного поля: сила постоянна.

Работа не зависит от формы траектории; работа по перемещению по замкнутой траектории равна нулю.

Для неоднородного поля:

Потенциал электрического поля– отношение работы, которое совершает поле, перемещая пробный электрический заряд в бесконечность, к величине этого заряда.

-потенциал– энергетическая характеристика поля. Измеряется в Вольтах

Разность потенциалов:

Если , то

, значит

-градиент потенциала.

Для однородного поля: разность потенциалов – напряжение:

. Измеряется в Вольтах, приборы – вольтметры.

Электроёмкость– способность тел накапливать электрический заряд; отношение заряда к потенциалу, которое для данного проводника всегда постоянно.

Не зависит от заряда и не зависит от потенциала. Но зависит от размеров и формы проводника; от диэлектрических свойств среды.

, гдеr– размер,- проницаемость среды вокруг тела.

Электроёмкость увеличивается, если рядом находятся любые тела – проводники или диэлектрики.

Конденсатор– устройство для накопления заряда. Электроёмкость:

Плоский конденсатор– две металлические пластины, между которыми находится диэлектрик. Электроёмкость плоского конденсатора:

, гдеS– площадь пластин,d– расстояние между пластинами.

Энергия заряженного конденсатораравна работе, которую совершает электрическое поле при переносе заряда с одной пластины на другую.

Перенос малого заряда , напряжение измениться на, совершится работа. Так как, а С =const,. Тогда. Интегрируем:

Энергия электрического поля:, гдеV=Sl– объём, занимаемый электрическим полем

Для неоднородного поля:.

Объёмная плотность электрического поля:. Измеряется в Дж/м3.

Электрический диполь– система, состоящая из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя -l).

Основная характеристика диполя – дипольный момент– вектор, равный произведению заряда на плечо диполя, направленный от отрицательного заряда к положительному. Обозначается. Измеряется в Кулон-метрах.

Диполь в однородном электрическом поле.

На каждый из зарядов диполя действуют силы: и. Эти силы противоположно направлены и создают момент пары сил – вращающий момент:, где

М – вращающий момент F– силы, действующие на диполь

d– плечо силl– плечо диполя

p– дипольный моментE– напряжённость

- угол междуpи Еq– заряд

Под действием вращающего момента, диполь повернётся и установится по направлению линий напряжённости. Векторы pи Е будут параллельны и однонаправлены.

Диполь в неоднородном электрическом поле.

Вращающий момент есть, значит диполь повернётся. Но силы будут неравны, и диполь будет двигаться туда, где сила больше.

-градиент напряжённости. Чем выше градиент напряжённости, тем выше боковая сила, которая стаскивает диполь. Диполь ориентируется вдоль силовых линий.

Собственное поле диполя.

Но . Тогда:

Пусть диполь находится в точке О, а его плечо мало. Тогда:

Формула получена с учётом:

Таким образом разность потенциалов зависит от синуса половинного угла, под которым видны точки диполя, и проекции дипольного момента на прямую, соединяющие эти точки.

Диэлектрики в электрическом поле.

Диэлектрик– вещество, не имеющее свободных зарядов, а значит и не проводящее электрический ток. Однако на самом же деле проводимость существует, но она ничтожно мала.

Классы диэлектриков:

с полярными молекулами (вода, нитробензол): молекулы не симметричны, центры масс положительных и отрицательных зарядов не совпадают, а значит, они обладают дипольным моментом даже в случае, когда электрического поля нет.
с неполярными молекулами (водород, кислород): молекулы симметричны, центры масс положительных и отрицательных зарядов совпадают, а значит, они не имеют дипольного момента при отсутствии электрического поля.
кристаллические (хлорид натрия): совокупность двух подрешёток, одна из которых заряжен положительно, а другая – отрицательно; в отсутствии электрического поля суммарный дипольный момент равен нулю.

Поляризация– процесс пространственного разделения зарядов, появления связанных зарядов на поверхности диэлектрика, что приводит к ослаблению поля внутри диэлектрика.

Способы поляризации:

1 способ – электрохимическая поляризация:

На электродах – движение к ним катионов и анионов, нейтрализация веществ; образуются области положительных и отрицательных зарядов. Ток постепенно уменьшается. Скорость установления механизма нейтрализации характеризуется временем релаксации – это время, в течение которого ЭДС поляризации увеличится от 0 до максимума от момента наложения поля. = 10-3-10-2с.

2 способ – ориентационная поляризация:

На поверхности диэлектрика образуются некомпенсированные полярные, т.е. происходит явление поляризации. Напряжённость внутри диэлектрика меньше внешней напряжённости. Время релаксации: = 10-13-10-7с. Частота 10 МГц.

3 способ – электронная поляризация:

Характерна для неполярных молекул, которые становятся диполями. Время релаксации: = 10-16-10-14с. Частота 108МГц.

4 способ – ионная поляризация:

Две решётки (NaиCl) смещаются относительно друг друга.

Время релаксации: =10-8-10-3с. Частота 1 КГц

5 способ – микроструктурная поляризация:

Характерен для биологических структур, когда чередуются заряженные и незаряженные слои. Происходит перераспределение ионов на полупроницаемых или непроницаемых для ионов перегородках.

Время релаксации: =10-8-10-3с. Частота 1 КГц

Числовые характеристики степени поляризации:

вектор поляризованности . Измеряется в Кл/л
относительная диэлектрическая проницаемость раз
Дисперсия – зависимость от частоты.

Электрический ток– это упорядоченное движение свободных зарядов в веществе или в вакууме.

Условия существования электрического тока:

наличие свободных зарядов
наличие электрического поля, т.е. сил, действующих на эти заряды

Сила тока– величина, равная заряду, который проходит через любое поперечное сечение проводника за единицу времени (1 секунду)

Измеряется в Амперах.

n– концентрация зарядов

q– величина заряда

S– площадь поперечного сечения проводника

- скорость направленного движения частиц.

Скорость движения заряженных частиц в электрическом поле небольшая – 7*10-5м/с, скорость распространения электрического поля 3*108м/с.

Плотность тока– величина заряда, проходящего за 1 секунду через сечение в 1 м2.

. Измеряется в А/м2.

- сила, действующая на ион со стороны эл поля равна силе трения

- подвижность ионов

- скорость направленного движения ионов =подвижность, напряжённость поля

Удельная проводимость электролита тем больше, чем больше концентрация ионов, их заряд и подвижность. При повышении температуры возрастает подвижность ионов и увеличивается электропроводность.

studfiles.net

Формула напряжённости электрического поля

$E = \frac{F}{q}$

Здесь – напряжённость электрического поля, 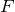– сила, действующая на заряд, – величина заряда.

Единица измерения напряжённости электрического поля – В/м (вольт на метр) или Н/Кл (ньютон на кулон).

Напряжённость – векторная величина, характеризующая интенсивность воздействия электрического поля на заряжённую частицу в конкретной точке. Напряжённость поля в различных точках вообще говоря различна, то есть электрическое поле – это векторное поле, направление векторов которого зависит от того, как было создано это поле. По указанной формуле можно рассчитать не только силу воздействия электрического поля на точечный заряд, но и силу воздействия этого поля на заряжённое тело, если распределение заряда в нём известно.

Примеры решения задач по теме «Напряжённость электрического поля»

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Электрический заряд

e=Кл

Точечный заряд – заряд тела, которое можно принять за материальную точку.

, гдеФ/м, Кл2/нм2– диэлектр. пост. вакуума

- относит. диэлектрическая проницаемость (>1)

- абсолютная диэлектрическая прониц. среды

Электрическое поле– материальная среда, через которую происходит взаимодействие электрических зарядов.

Свойства электрического поля:

Электрическое поле существует вокруг любого заряда. Если заряд неподвижен – поле электростатическое.
Электрическое поле действует на любой помещённый в него заряд согласно закону Кулона. Обнаружить электрическое поле можно только по его действию на другие заряды.
Электрическое поле существует в любой среде и распространяется с конечной скоростью: м/с.
Электрическое поле не имеет чётких границ. Действие его уменьшается при увеличении расстояния от заряда, его создающего.

Характеристики электрического поля:

Напряжённость(E) – векторная величина, равная силе, действующей на единичный пробный заряд, помещённый в данную точку.

Измеряется в Н/Кл.

Направление – такое же, как и у действующей силы.

Напряжённость не зависитни от силы, ни от величины пробного заряда.

Графическиэлектронное поле изображают с помощью линий напряжённости.

Виды полей:

Однородное электрическое поле– поле, вектор напряжённости которого в каждой точке одинаков по модулю и направлению.

+ -

Неоднородное электрическое поле– поле, вектор напряжённости которого в каждой точке неодинаков по модулю и направлению.

Постоянное электрическое поле– вектор напряжённости не изменяется.
Непостоянное электрическое поле– вектор напряжённости изменяется.

Работа электрического поля по перемещению заряда.

, гдеF– сила,S– перемещение,- угол междуFиS.

Для однородного поля: сила постоянна.

Работа не зависит от формы траектории; работа по перемещению по замкнутой траектории равна нулю.

Для неоднородного поля:

Потенциал электрического поля– отношение работы, которое совершает поле, перемещая пробный электрический заряд в бесконечность, к величине этого заряда.

-потенциал– энергетическая характеристика поля. Измеряется в Вольтах

Разность потенциалов:

Если , то

, значит

-градиент потенциала.

Для однородного поля: разность потенциалов – напряжение:

. Измеряется в Вольтах, приборы – вольтметры.

, гдеr– размер,- проницаемость среды вокруг тела.

Электроёмкость увеличивается, если рядом находятся любые тела – проводники или диэлектрики.

Конденсатор– устройство для накопления заряда. Электроёмкость:

, гдеS– площадь пластин,d– расстояние между пластинами.

Перенос малого заряда , напряжение измениться на, совершится работа. Так как, а С =const,. Тогда. Интегрируем:

Энергия электрического поля:, гдеV=Sl– объём, занимаемый электрическим полем

Для неоднородного поля:.

Объёмная плотность электрического поля:. Измеряется в Дж/м3.

Диполь в однородном электрическом поле.

М – вращающий момент F– силы, действующие на диполь

d– плечо силl– плечо диполя

p– дипольный моментE– напряжённость

- угол междуpи Еq– заряд

Диполь в неоднородном электрическом поле.

Собственное поле диполя.

Но . Тогда:

Пусть диполь находится в точке О, а его плечо мало. Тогда:

Формула получена с учётом:

Диэлектрики в электрическом поле.

Классы диэлектриков:

с полярными молекулами (вода, нитробензол): молекулы не симметричны, центры масс положительных и отрицательных зарядов не совпадают, а значит, они обладают дипольным моментом даже в случае, когда электрического поля нет.
с неполярными молекулами (водород, кислород): молекулы симметричны, центры масс положительных и отрицательных зарядов совпадают, а значит, они не имеют дипольного момента при отсутствии электрического поля.
кристаллические (хлорид натрия): совокупность двух подрешёток, одна из которых заряжен положительно, а другая – отрицательно; в отсутствии электрического поля суммарный дипольный момент равен нулю.

Способы поляризации:

1 способ – электрохимическая поляризация:

2 способ – ориентационная поляризация:

3 способ – электронная поляризация:

Характерна для неполярных молекул, которые становятся диполями. Время релаксации: = 10-16-10-14с. Частота 108МГц.

4 способ – ионная поляризация:

Две решётки (NaиCl) смещаются относительно друг друга.

Время релаксации: =10-8-10-3с. Частота 1 КГц

5 способ – микроструктурная поляризация:

Время релаксации: =10-8-10-3с. Частота 1 КГц

Числовые характеристики степени поляризации:

вектор поляризованности . Измеряется в Кл/л
относительная диэлектрическая проницаемость раз
Дисперсия – зависимость от частоты.

Электрический ток– это упорядоченное движение свободных зарядов в веществе или в вакууме.

Условия существования электрического тока:

наличие свободных зарядов
наличие электрического поля, т.е. сил, действующих на эти заряды

Измеряется в Амперах.

n– концентрация зарядов

q– величина заряда

S– площадь поперечного сечения проводника

- скорость направленного движения частиц.

Плотность тока– величина заряда, проходящего за 1 секунду через сечение в 1 м2.

. Измеряется в А/м2.

- сила, действующая на ион со стороны эл поля равна силе трения

- подвижность ионов

- скорость направленного движения ионов =подвижность, напряжённость поля

studfiles.net

Напряженность электрического поля

Электротехника: Основы

Напряженность электрического поля

Сила порождаемая электрическими зарядами

Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.

Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.

Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы. Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля. В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.

Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях. Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля. Пробный заряд имеет некоторое количество заряда и обозначается символом q.

При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы - или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.

Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как

Стандартные метрические единицы измерения напряженности электрического поля возникают из его определения. Таким образом напряженность электрического поля определяется как сила равная 1 Ньютону (Н) деленному на 1 Кулон (Кл). Напряженность электрического поля измеряется в Ньютон/Кулон или иначе Н/Кл. В системе СИ также измеряется в Вольт/метр. Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.

В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).

Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет. Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q - скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза. Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз. Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.

Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.

Более подробно о формуле напряженности электрического поля

Выше мы коснулись определения напряженности электрического поля в том, как она измеряется. Теперь мы попробуем исследовать более развернутое уравнение с переменными, чтобы яснее представить саму суть вычисления и измерения напряженности электрического поля. Из уравнения мы сможем увидеть, что именно влияет, а что нет. Для этого нам прежде всего потребуется вернутся к уравнению Закона Кулона.

Закон Кулона утверждает, что электрическая сила F между двумя зарядами прямо пропорциональна произведению количества этих зарядов и обратно пропорциональна квадрату расстояния между их центрами.

Если внести в уравнение Закона Кулона два наших заряда Q (источник) и q (пробный заряд), тогда мы получим следующую запись:

Если выражение для электрической силы F, как она определяется Законом Кулона подставить в уравнение для напряженности электрического поля E, которое приведено выше, тогда мы получим следующее уравнение:

Уравнение напряженности электрического поля

Обратите внимание, что пробный заряд q был сокращен, то есть убран как в числителе так и в знаменателе. Новая формула для напряженности электрического поля E выражает напряженность поля в терминах двух переменных, которые влияют на нее. Напряженность электрического поля зависит от количества исходного заряда Q и от расстоянии от этого заряда d до точки пространства, то есть геометрического места, в котором и определяется значение напряженности. Таким образом у нас появилась возможность характеризовать электрическое поле через его напряженность.

Закон обратных квадратов

Как и все формулы в физике, формулы для напряженности электрического поля могут быть использованы для алгебраического решения задач (проблем) физики. Точно также, как и любую другую формулу в ее алгебраической записи, можно исследовать и формулу напряженности электрического поля. Такое исследование способствует более глубокому пониманию сути физического явления и характеристик этого явления. Одна из особенностей формулы напряженности поля является то, что она иллюстрирует обратную квадратичную зависимость между напряженностью электрического поля и расстоянием до точки в пространстве от источника поля. Сила электрического поля, создаваемого в источнике заряде Q обратно пропорционально квадрату расстояния от источника. Иначе говорят, что искомая величина обратно пропорциональна квадрату.

Напряженность электрического поля зависит от геометрического места в пространстве, и ее величина уменьшается с увеличением расстояния. Так, например, если расстояние увеличится в 2 раза, то напряженность уменьшится в 4 раза (22), если расстояния между уменьшится в 2 раза, то напряженность электрического поля увеличится в 4 раза (22). Если же расстояние увеличивается в 3 раза, то напряженность электрического поля уменьшается в 9 раз (32). Если расстояние увеличивается в 4 раза, то напряженность электрического поля уменьшается в 16 (42).

Направление вектора напряженности электрического поля

Как упоминалось ранее, напряженность электрического поля является векторной величиной. В отличие от скалярной величиной, векторная величина является не полностью описанной, если не определено ее направление. Величина вектора электрического поля рассчитывается как величина силы на любой пробный заряд, расположенный в электрическом поле.

Сила, действующая на пробный заряд может быть направлена либо к источнику заряда или непосредственно от него. Точное направление силы зависит от знаков пробного заряд и источника заряда, имеют ли они тот же знак заряда (тогда происходит отталкивание) или же их знаки противоположные (происходит притяжение). Чтобы решить проблему направления вектора электрического поля, направлен он к источнику или от источника были приняты правила, которые используются всеми учеными мира. Согласно этим правилам направление вектора всегда от заряда с положительным знаком полярности. Это можно представить в виде силовых линий, которые выходят из зарядов положительных знаков и заходят в заряды отрицательных знаков.

Дата: 29.04.2015

Тег статьи: Электричество

Все теги раздела Электротехника:Электричество Закон Ома Электрический ток Электробезопасность Устройства Биоэлектричество Характеристики Физические величины Электролиз Электрические схемы Асинхронные двигатели

www.electricity-automation.com

Электрический заряд

e=Кл

Точечный заряд – заряд тела, которое можно принять за материальную точку.

, гдеФ/м, Кл2/нм2– диэлектр. пост. вакуума

- относит. диэлектрическая проницаемость (>1)

- абсолютная диэлектрическая прониц. среды

Электрическое поле– материальная среда, через которую происходит взаимодействие электрических зарядов.

Свойства электрического поля:

Электрическое поле существует вокруг любого заряда. Если заряд неподвижен – поле электростатическое.
Электрическое поле действует на любой помещённый в него заряд согласно закону Кулона. Обнаружить электрическое поле можно только по его действию на другие заряды.
Электрическое поле существует в любой среде и распространяется с конечной скоростью: м/с.
Электрическое поле не имеет чётких границ. Действие его уменьшается при увеличении расстояния от заряда, его создающего.

Характеристики электрического поля:

Напряжённость(E) – векторная величина, равная силе, действующей на единичный пробный заряд, помещённый в данную точку.

Измеряется в Н/Кл.

Направление – такое же, как и у действующей силы.

Напряжённость не зависитни от силы, ни от величины пробного заряда.

Графическиэлектронное поле изображают с помощью линий напряжённости.

Виды полей:

Однородное электрическое поле– поле, вектор напряжённости которого в каждой точке одинаков по модулю и направлению.

+ -

Неоднородное электрическое поле– поле, вектор напряжённости которого в каждой точке неодинаков по модулю и направлению.

Постоянное электрическое поле– вектор напряжённости не изменяется.
Непостоянное электрическое поле– вектор напряжённости изменяется.

Работа электрического поля по перемещению заряда.

, гдеF– сила,S– перемещение,- угол междуFиS.

Для однородного поля: сила постоянна.

Работа не зависит от формы траектории; работа по перемещению по замкнутой траектории равна нулю.

Для неоднородного поля:

Потенциал электрического поля– отношение работы, которое совершает поле, перемещая пробный электрический заряд в бесконечность, к величине этого заряда.

-потенциал– энергетическая характеристика поля. Измеряется в Вольтах

Разность потенциалов:

Если , то

, значит

-градиент потенциала.

Для однородного поля: разность потенциалов – напряжение:

. Измеряется в Вольтах, приборы – вольтметры.

, гдеr– размер,- проницаемость среды вокруг тела.

Электроёмкость увеличивается, если рядом находятся любые тела – проводники или диэлектрики.

Конденсатор– устройство для накопления заряда. Электроёмкость:

, гдеS– площадь пластин,d– расстояние между пластинами.

Перенос малого заряда , напряжение измениться на, совершится работа. Так как, а С =const,. Тогда. Интегрируем:

Энергия электрического поля:, гдеV=Sl– объём, занимаемый электрическим полем

Для неоднородного поля:.

Объёмная плотность электрического поля:. Измеряется в Дж/м3.

Диполь в однородном электрическом поле.

М – вращающий момент F– силы, действующие на диполь

d– плечо силl– плечо диполя

p– дипольный моментE– напряжённость

- угол междуpи Еq– заряд

Диполь в неоднородном электрическом поле.

Собственное поле диполя.

Но . Тогда:

Пусть диполь находится в точке О, а его плечо мало. Тогда:

Формула получена с учётом:

Диэлектрики в электрическом поле.

Классы диэлектриков:

с полярными молекулами (вода, нитробензол): молекулы не симметричны, центры масс положительных и отрицательных зарядов не совпадают, а значит, они обладают дипольным моментом даже в случае, когда электрического поля нет.
с неполярными молекулами (водород, кислород): молекулы симметричны, центры масс положительных и отрицательных зарядов совпадают, а значит, они не имеют дипольного момента при отсутствии электрического поля.
кристаллические (хлорид натрия): совокупность двух подрешёток, одна из которых заряжен положительно, а другая – отрицательно; в отсутствии электрического поля суммарный дипольный момент равен нулю.

Способы поляризации:

1 способ – электрохимическая поляризация:

2 способ – ориентационная поляризация:

3 способ – электронная поляризация:

Характерна для неполярных молекул, которые становятся диполями. Время релаксации: = 10-16-10-14с. Частота 108МГц.

4 способ – ионная поляризация:

Две решётки (NaиCl) смещаются относительно друг друга.

Время релаксации: =10-8-10-3с. Частота 1 КГц

5 способ – микроструктурная поляризация:

Время релаксации: =10-8-10-3с. Частота 1 КГц

Числовые характеристики степени поляризации: