ЛАБОРАТОРНАЯ РАБОТА № 6 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПОЛЕЗНОЙ МОЩНОСТИ, К.П.Д. ИСТОЧНИКА ТОКА И СИЛЫ ТОКА В ЦЕПИ ОТ НАГРУЗКИ Цель работы - исследование зависимости полезной мощности, к.п.д. источника тока и силы тока в цепи от нагрузки. Приборы и принадлежности: исследуемый источник тока, реостат, вольтметр, амперметр и ключ. Краткие сведения из теории При комнатной температуре (Т ≈ 300 К) электроны проводимости в металле можно рассматривать как классические частицы массой m и зарядом е, равномерно распределенные по объему проводника. Они находятся в постоянном хаотическом тепловом движении и взаимодействуют с атомами проводника только при столкновениях. Взаимодействием между электронами можно пренебречь. Движение электронов проводимости по объему проводника аналогично движению молекул газа, поэтому очень часто говорят, что электроны проводимости образуют в металле «электронный газ». Так как движение электронов проводимости при отсутствии внешних полей хаотично, средняя скорость теплового движения электронов < u > равна нулю. Однако после включения внешнего однородного электрического поля напряженностью Е на электроны проводимости действует сила F = — еЕ, которая одинакова для всех электронов. Под действием этой силы электроны получают дополнительную скорость υ в противоположном вектору Е направлении (см. рис. 6.1). Среднее время τ, в течение которого электрон проводимости движется в поле Е между двумя столкновениями с ионами проводника, называется временем свободного пробега. Рис. 6.1 Будем считать, что в результате столкновения с атомом металла электрон полностью теряет дополнительную скорость υ, которую он приобрел в электрическом поле. Из классической теории электропроводности металлов следует, что удельное сопротивление проводника можно вычислить по формуле , (6.1) где n — число электронов проводимости в единице объема. Рассмотрим движение электрона проводимости после столкновения с атомом решетки проводника. В начальный момент его дополнительная скорость υ равна нулю. Ускорение, с которым движется электрон в электрическом поле, равно a = E. Это значит, что за время свободного пробега дополнительная скорость электрона увеличится от 0 до величины υmax: υmax = Eτ, а его полная скорость составит u' = u + υmax. В результате столкновения с атомом решётки проводника электрон теряет дополнительную скорость υmax, увеличивая энергию колебаний атомов решетки. За время свободного пробега τ каждый электрон в среднем один раз сталкивается с атомами кристаллической решетки и передает им энергию: . Общее количество энергии, которое получат атомы решетки за время τ, будет равно: , где V — объем проводника. Иначе говоря, полная мощность Р, рассеиваемая в проводнике, вычисляется по формуле . Она равна энергии, которую получают атомы проводника от электронов проводимости в единицу времени. Выразим мощность Р, рассеиваемую во всем объеме проводника, используя формулу (6.1), в следующем виде: , где j – плотность тока (j = E – закон Ома в дифференциальной форме). Учитывая, что для цилиндрического проводника объем V = SL и падение напряжения U = EL, получим: (закон Джоуля - Ленца), где. Мощность, выделяемая в единице объема, вычисляется по формуле(закон Джоуля - Ленца в дифференциальной форме). Таким образом, в рамках классической теории электропроводности получен закон Джоуля - Ленца. На основании предыдущего рассмотрения движения электронов в проводнике можно сделать следующий вывод. В рамках классической теории выделение тепла в проводнике при протекании по нему электрического тока объясняется увеличением энергии колебаний атомов решетки проводника в результате столкновений с электронами проводимости, ускоренными в электрическом поле. Рассмотрим цепь, состоящую из источника тока с внутренним сопротивлением R0 и электродвижущей силой Э0 (см. рис. 6.2) и резистора с переменным сопротивлением R. Рис. 6.2 Сила тока в цепи . (6.2) Мощность, расходуемая во внешнем участке цепи, называется полезной мощностью источника тока, так как она может быть использована для практических целей. Она равна , (6.3) где U — падение напряжения на внешнем сопротивлении R. Полная мощность источника тока . Коэффициент полезного действия источника тока . (6.4) С учетом формулы (6.2) и того, что U = IR, выражения для полезной мощности и к.п.д. примут следующий вид: . (6.5) Исследование выражений (6.2) и (6.5) показывает, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального к.п.д. противоречивы (см. рис. 6.3). Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и к.п.д.: почти вся совершаемая источником работа идет на выделение тепла во внутреннем сопротивлении. Чтобы получить максимальную полезную мощность, следует взять нагрузку с сопротивлением, равным внутреннему сопротивлению источника, но величина к.п.д. при этом составит только 0,5. Любую полезную мощность, меньшую максимальной, можно получить при двух значениях сопротивления нагрузки. В практических целях для получения заданной полезной мощности в этом случае следует выбирать нагрузку с большим сопротивлением, так как к.п.д. при этом выше. Рис. 6.3 Описание экспериментальной установки Схема установки представлена на рис.6.2. В цепь источника постоянного тока включены реостат R, электроизмерительные приборы (амперметр А и вольтметр V) и ключ К. Порядок выполнения работы Собрать схему, изображенную на рис.6.2. Выбрать предел измерений по амперметру и записать в протокол наблюдений: а) предел измерений амперметра в амперах; б) число делений по шкале амперметра; в) класс точности амперметра; Повторить выбор предела измерений для вольтметра и записать в протокол наблюдений его параметры. Изменяя сопротивление реостата R, снять отсчеты по амперметру и вольтметру, соответствующие каждому положению движка реостата (всего 15 точек). Результаты занести в таблицу (см. табл. 6.1). Разомкнуть внешнюю цепь ключом К и измерить вольтметром электродвижущую силу источника Э0. Результат занести в протокол наблюдений. U I (эксп.) I (теор.), А R, Ом Р, Вт η дел. В дел. А Обработка и анализ результатов измерений Вычислить значения полезной мощности источника Р по формуле (6.3), к.п.д. источника тока η — (6.4) и сопротивления R — по формуле . Результаты вычислений занести в таблицу (табл. 6.1). Построить графики зависимостей P = P(R), η = η(R), I = I(R). Определить ошибки измерения силы тока ΔI и напряжения ΔU по формулам погрешности прямых измерений (с учетом класса точности приборов). Затем определить погрешности измерения сопротивления внешней цепи ΔR, полезной мощности ΔР и к.п.д. источника Δη, используя формулы Погрешности измерения силы тока, полезной мощности, к.п.д. и внешнего сопротивления отразить на графиках, построив на каждом прямоугольники ошибок для трех экспериментальных значений. Вычислить величину внутреннего сопротивления источника, используя формулу для нескольких (пяти — шести) значений пар величинU и I. При расчете не следует использовать результаты измерений, соответствующие малым токам, так как при этом величина Э0— U мала и ошибка определения R0 значительна. Усреднить полученные значения R0. Используя формулу (6.2), определить теоретические значения силы тока в цепи и на одном графике построить теоретические и экспериментальные зависимости силы тока I от внешнего сопротивления цепи R. Контрольные вопросы Каков механизм выделения тепла в проводнике при протекании по нему электрического тока? Привести формулировки закона Джоуля - Ленца в интегральной и дифференциальной формах. Сформулировать закон Ома для участка цепи, содержащего источник э.д.с., и для замкнутой цепи. При какой величине внешнего сопротивления цепи полезная мощность источника тока максимальна (вывести)? Библиогр.: [2] гл. VIII, § 8.5; гл. IX, §§ 9.2, 9.3; [6] гл. V, §§ 34, 35, 37, 38. studfiles.net ЗАВИСИМОСТЬ МОЩНОСТИ И КПД ИСТОЧНИКА ТОКА ОТ НАГРУЗКИ Приборы и принадлежности: лабораторная панель, два аккумулятора, миллиамперметр, вольтметр, переменные резисторы. Введение. Наиболее широко распространенными источниками постоянного тока являются гальванические элементы, аккумуляторы, выпрямители. Присоединим к источнику тока ту часть, которая нуждается в его электрической энергии (лампочка, радиоприемник, микрокалькулятор и т.п.). Эта часть электрической цепи называется общим словом – нагрузкой. Нагрузка обладает некоторым электрическим сопротивлением R и потребляет от источника ток силой I (рис.1). Нагрузка образует внешнюю часть электрической цепи. Но есть и внут-ренняя часть цепи – это фактически сам источник тока, он имеет электрическое сопротивлениеr, в нем протекает тот же ток I. Границей между внутренним и внешним участками цепи являются клеммы “+” и “–” источника тока, к которым присоединяется потребитель Рис.1 электрической энергии (нагрузка). На рисунке 1 источник тока охвачен штриховым контуром. Источник тока с электродвижущей силой Е создает в замкнутой цепи ток, сила которого определяется законом Ома: (1) При протекании тока по сопротивлениям R и r в них выделяется тепловая энергия, определяемая законом Джоуля-Ленца. Мощность во внешней части цепи Ре – внешняя мощность . (2) Эта мощность является полезной. Мощность во внутренней части Рi – внутренняя мощность. Она недоступна для использования и поэтому составляет потери мощности источника . (3) Полная мощность источника тока Р есть сумма этих двух слагаемых, (4) Как видно из определений (2,3,4), каждая из мощностей зависит и от протекающего тока и от сопротивления соответствующей части цепи. Рассмотрим эту зависимость по отдельности. Зависимость мощности Pe , Pi , P от тока нагрузки. С учетом закона Ома (1) полную мощность можно записать так: . (5) Таким образом, полная мощность источника прямо пропорциональна потребляемому току. Мощность, выделяющаяся на нагрузке (внешняя), есть . (6) Она равна нулю в двух случаях: 1) I = 0 и 2) E – Ir = 0. (7) Первое условие справедливо для разомкнутой цепи, когда R , второе соответствует так называемому короткому замыканию источника, когда сопротивление внешней цепи R = 0. При этом ток в цепи (см. формулу (1)) достигает наибольшего значения – тока короткого замыкания. (8) Рнб=EIкз=Е2/r. (9) Однако вся она выделяется внутри источника. Выясним, при каких условиях внешняя мощность становится макси-мальной. Зависимость мощности Pe от тока является (см. формулу (6)) параболической: . Положение максимума функции определим из условия: dPe/dI = 0, dPe/dI = E – 2Ir. Полезная мощность достигает максимального значения при токе (10) что составляет половину тока короткого замыкания (8), (см. рис. 2): (11) Внешняя мощность при этом токе составляет (12) т.е. максимальная внешняя мощность составляет четвертую часть наибольшей полной мощности источника. Мощность, выделяющаяся на внутреннем сопротивлении при токе Imax, определяется следующим образом: , (13) т.е. составляет тоже одну четверть наибольшей полной мощности источника тока. Заметим, что при токе Imax Pe = Pi . (14) Когда ток в цепи стремится к наибольшему значению Iкз, внутренняя мощность т.е. равна наибольшей мощности источника (9). Это означает, что вся мощность источника выделяется на его внутреннемсопротивлении, что, разумеется , вредно с точки зрения сохранности источника тока. Характерные точки графика зависимости Pe= Pe(I) показаны на рис. 2. Рис.2 Рис. 3 Эффективностьработы источника тока оценивается егокоэффициентом полезного действия. КПД есть отношение полезной мощности к полной мощности источника: = Pe/ P. Используя формулу (6), выражение для КПД можно записать следующим образом: . (15) Из формулы (1) видно, что E – Ir = IR есть напряжение U на внешнем сопротивлении. Следовательно, КПД = U/E . (16) Из выражения (15) также следует, что = (17) т.е. КПД источника зависит от тока в цепи и стремится к наибольшему значению, равному единице, при токе I 0 (рис.3). С увеличением силы тока КПД уменьшается по линейному закону и обращается в нуль при коротком замыкании, когда ток в цепи становится наибольшим Iкз = E/r . Из параболического характера зависимости внешней мощности от тока (6) следует, что одна и та же мощность на нагрузке Pe может быть получена при двух различных значениях тока в цепи. Из формулы (17) и из графика (рис.3) видно, что с целью получения от источника большего КПД предпочтительна работа при меньших токах нагрузки, там этот коэффициент выше. studfiles.net Будем считать, что в результате столкновения с атомом металла электрон полностью теряет дополнительную скорость v, которую он приобрел в электрическом поле. Из классической теории электропроводности металлов следует, что удельное сопротивление проводника можно вычислить по формуле где n – число электронов проводимости в единице объема. Рассмотрим движение электрона проводимости после столк- новения с атомом решетки проводника. В начальный момент его дополнительная скорость v равна нулю. Ускорение, с которым движется электрон в электрическом поле, равно a = − me E. Это значит, что за время свободного пробега дополнительная скорость электрона увеличится от нуля до величины vmax: vmax = − me Eτ, а его полная скорость составитu' = u + vmax. В результате столкновения с атомом решётки проводника электрон теряет дополнительную скорость vmax, увеличивая энергию колебаний атомов решетки. За время свободного пробегаτ каждый электрон в среднем один раз сталкивается с атомами кристаллической решетки и передает им энергию: w = mu'2 − mu 2 = mυ2max. 2 2 2 Общее количество энергии, которое получат атомы решетки за время τ, будет равно:Q = nwV , гдеV – объем проводника. Иначе говоря, полная мощность Р, рассеиваемая в проводнике, вычисляется по формуле P = Q = nVe2 E2 τ . τ 2m Она равна энергии, которую получают атомы проводника от электронов проводимости в единицу времени. Выразим мощность Р, рассеиваемую во всем объеме проводника, используя формулу (6.1) как P = ρ1 E2V=ρj2V, studfiles.net Цель работы: опытное определение ЭДС и внутреннего сопротивления источника тока. Изучение зависимости полезной, полной мощности и КПД источника тока от величины нагрузки. Теоретическое введение Электрический ток проводимости возникает под действием электрического поля. Носителями электрического тока в металлах являются свободные электроны. Основной характеристикой электрического тока является сила тока. Силой тока называется скалярная физическая величина, равная отношению заряда dq, переносимого через рассматриваемую поверхность (сечение проводника) за некоторый малый промежуток времени dt , к длительности этого промежутка: Для участка цепи экспериментально было установлено, что сила тока пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника (закон Ома): где U – напряжение на концах проводника, R – электрическое сопротивление. Для поддержания в цепи постоянного тока проводимости необходимо, чтобы на носители тока действовали, помимо кулоновских сил, еще какие-то иные, неэлектрические, силы, называемые сторонними силами. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных веществ, электрическими (но не электростатическими) полями, порожденными меняющимися во времени магнитными полями и т.д. Под действием создаваемого поля сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему на концах цепи поддерживается постоянная разность потенциалов и в цепи течет постоянный электрический ток. Сторонние силы можно охарактеризовать работой, которую они совершают над перемещающимися по цепи зарядами. Физическая величина, определяемая отношением работы, совершаемой сторонними силами по перемещению заряда вдоль цепи, к величине этого заряда, называется электродвижущей силой (ЭДС) Электрическая цепь состоит, как правило, из источника тока, подводящих проводов и потребителя тока или нагрузки. Ток в замкнутой цепи определяется по закону Ома: где r – внутреннее сопротивление источника тока, R – сопротивление внешней цепи, т.е. сопротивление подводящих проводов и нагрузки. Как правило, сопротивление подводящих проводов мало, и им часто пренебрегают. При прохождении тока по цепи совершается работа. Так как работа кулоновских сил по перемещению заряда по замкнутой цепи равна нулю (электростатическое поле потенциально), то работа по перемещению заряда dq по замкнутой цепи будет определяться только работой сторонних сил и будет равна, как следует из (8.3), Разделив работу dA на время dt, за которое она совершается, получим мощность, развиваемую источником тока: Подставив в эту формулу вместо тока I его значение из (8.4), получим для полной мощности, выделяемой во всей цепи, выражение В нагрузке выделяется только часть этой мощности: Здесь dAН – работа по переносу заряда на однородном участке цепи с разностью потенциалов Δφ=U=RI. Мощность РН назовем полезной мощностью. Остальная мощность расходуется в источнике тока и оказывается бесполезной. Отношение полезной мощности ко всей мощности P, развиваемой ЭДС в цепи, определяет коэффициент полезного действия (КПД) источника тока: Из этой формулы следует, что КПД будет тем больше, чем больше сопротивление нагрузки R по сравнению с сопротивлением источника r. Поэтому сопротивление источника тока стремятся сделать как можно меньшим. Мощность, развиваемая данным источником тока, зависит от сопротивления нагрузки R. Она максимальна при коротком замыкании (R®0, см. формулу (8.7)): но в этом случае вся мощность выделяется в самом источнике и оказывается совершенно бесполезной. С ростом сопротивления нагрузки R полная мощность убывает, стремясь к нулю при R ® ¥. Можно получить соотношение, при котором полезная мощность, отбираемая от данного источника тока, будет наибольшей. Для этого нужно выражение (8.8) по R и приравнять производную к нулю: Отсюда находим, что РН имеет максимум при R=r (другое решение R = ¥ соответствует минимуму РН). Следовательно, чтобы отобрать от данной ЭДС наибольшую полезную мощность, нужно взять сопротивление нагрузки, равное сопротивлению источника тока. КПД при этом, как следует из (8.9), равен 0.5. Экспериментальная часть Приборы и оборудование: источник тока, амперметр, вольтметр, реостат. cyberpedia.su Если магазин МСР-63,т.е. внешнее сопротивление, отключен от источника тока, то какую величину измеряет вольтметр, подключенный к источнику ? 5********************************************************************* Электродвижущую силу Напряжение на зажимах* Напряжение на внутреннем сопротивлении Силу тока ********************************************************************** Цифровой вольтметр имеет очень большое сопротивление. Можно ли считать, что при его подсоединении к зажимам источника вместо внешнего сопротивления, он покажет чему равна ЭДС ? 5********************************************************************** Да* Нет *********************************************************************** Формулы мощностей имеют вид : P2=I*I*Rвн , P1=I*U , P=I*E. Как они называются ? 5********************************************************************* Мощность потерь,полезная мощность, полная мощность* Полезная мощность, полная мощность, мощность потерь Полная мощность, мощность потерь, полезная мощность ********************************************************************** Какой вид имеют графики полной, полезной и мощности потерь в зависимости от тока ? 5********************************************************************** Паpаболический,линейный, параболический Линейный, параболический,паpаболический* Параболический, параболический, линейный ********************************************************************** При каком соотношении внешнего R и внутреннего Rвн сопротивлений во внешней цепи выделяется максимальная полезная мощность ? 5********************************************************************* R>Rвн R<Rвн R=Rвн* ********************************************************************** Какой вид имеет график зависимости КПД от тока ? 5********************************************************************** Линейный с отрицательным наклоном* Линейный с положительным наклоном Нелинейный *********************************************************************** Чему равен КПД, если полезная мощность максимальна ? 5*********************************************************************** 0% 50%* 100% 25% ********************************************************************** График напpяжения пересекает ось напряжений в точке 1 В и ось тока в точке 1 А.Чему равно внутреннее сопротивление Rвн источника тока ? 20*********************************************************************** 4 Ом 3 Ом 2 Ом 1 Ом* ********************************************************************** Полезная мощность максимальна при токе 0,5 А. Внутреннее сопротивление Rвн равно 1 Ом. Чему равна эта полезная мощность ? 20********************************************************************** 1 Вт 0,5 Вт 0,25 Вт* 0,75 Вт ********************************************************************** Полезная мощность максимальна при токе 0,5 А. Внутреннее сопротивление Rвн равно 1 Ом. Чему равно напряжение на зажимах ? 20********************************************************************** 1 В 0,5 В* 0,25 В 0,75 В 1,25 В ********************************************************************** Можно ли от источника тока отбирать энергию с КПД 100% ? 5********************************************************************* Да Нет* ********************************************************************** При максимуме полезной мощности полезная мощность равна 10******************************************************************** половине полной мощности* полной мощности половине потерь мощности внутри источника ********************************************************************** Каково по величине внутреннее сопротивление аккумулятора? 10******************************************************************** десятки Ом единицы Ом сотые доли Ом* ********************************************************************** Потеря мощности внутри источника равна 10******************************************************************** I^2 * R I^2 * r* E*I - I^2 * r ********************************************************************** Коэффициентом полезного действия источника называется отношение 10******************************************************************** полной мощности источника к его полезной мощности полезной мощности источника к потерям мощности внутри источника полезной мощности источника к его полной мощности* ********************************************************************** ЭДС батареи численно равна 10******************************************************************** работе по перемещению единицы заряда по всей цепи* работе по перемещению единицы заряда на внешнем участке цепи силе, действующей на единицу заряда ********************************************************************* Полезной мощностью является мощность, развиваемая источником во 10******************************************************************* внутренней цепи всей цепи внешней цепи* ********************************************************************* График зависимости U = f(I) для некоторой цепи представляет собой прямую, пересекающую ось U при значении 2.2 В , а ось I - при 10 A. Определить (в указанной последовательности): ЭДС источника, ток короткого замыкания, внутреннее сопротивление источника и внешнее сопротивление цепи - для получения максимальной полезной мощности. 15******************************************************************* 2.0 В; 10 A; 0.2 Om; 0.4 Om 0.22 В; 1 A; 2.2 Om; 0.22 Om 2.2 В; 10 A; 0.22 Om; 0.22 Om* ********************************************************************* Чтобы определить, является ли полезная мощность максимальной, при значении силы тока Iм = Е / 2*r , необходимо вычислить 15******************************************************************* первую производную от Р1 по I* вторую производную от Р2 по I вторую производную от Р1 по I ********************************************************************* Чему равна сила тока в цепи при "коротком замыкании" ? 10******************************************************************* E / R E / 2*r Е / r* ********************************************************************* Чему pавно максимальное значение полезной мощности для источника с ЭДС Е=4О В и внутpенним сопpотивлением r=5 Ом? 15******************************************************************** 2О Вт 80 Вт* 16О Вт 32О Вт ************************************************************************ Внутpеннее сопpотивление источника 2 Ом. Пpи каком значении внешнего сопpотивления R (Ом) полезная мощность будет pавна мощности потеpь? 1О********************************************************************** 0 1 2* 4 бесконечном *********************************************************************** Пpи каком токе вся энеpгия электp. тока в цепи идет на pазогpев источника? 5*********************************************************************** пpи I = 0 пpи I -> к бесконечности пpи I = Iк/2 пpи I = Iк* ************************************************************************* studfiles.net Лабораторная работа №10-Э ОПРЕДЕЛЕНИЕ УСЛОВИЙ ЭКОНОМИЧНОГО ИСПОЛЬЗОВАНИЯ ИСТОЧНИКА ТОКА Цель работы - экспериментальная проверка теоретических выводов о наиболее экономичном использовании энергии источника тока. Теоретический анализ проблемы. Экономичное использование источника тока предусматривает создание таких условий, при которых будут достаточно высокими, с одной стороны - полезная мощность, а с другой стороны - коэффициент полезного действия. Теоретический расчёт показывает, что совместить эти два требования практически не возможно, а можно только обеспечить оптимальное соотношение для этих двух параметров. Действительно, простой расчёт показывает, что мощность Ра, выделяемая источником тока с ЭДС e во внешней цепи, то есть полезная мощность, будет максимальной, если сопротивление R внешней нагрузки равно внутреннему сопротивлению r источника тока: Ра = I2R = e2 Максимальное значение полезной мощности равно: Раmax = Коэффициент полезного действия (КПД) по определению равен: h = где Р = I2(R+r) - полная мощность, выделяемая источником тока. При R=r КПД равен: h = 50%. Остальные 50% мощности выделяются внутри источника тока, что приводит к большим потерям энергии на бесполезный разогрев источника тока, перегреву его внутренних частей и выходу источника тока из строя. Понятно, что повышения КПД источников тока является важнейшим требованием при эксплуатации силовых электрических установок. Чем меньше внутреннее сопротивление источника тока, тем выше его КПД. Таким образом, при R > r полезная мощность по абсолютному значению хотя и уменьшается, но её доля в полной мощности, выделяемой источником тока, возрастает, что экономически оказывается более выгодным. Однако, повышение КПД ограничивается тем, что, например, уже при R=5r и h = 83%, полезная мощность составляет всего 55% от максимально возможного значения (при R=r). А в пределе при R ® ¥, хотя КПД h ® 1, что очень выгодно, но вся мощность при этом выделяется внутри источника тока, а полезная мощность Ра® 0, что, естественно, не допустимо. Таким образом, в каждой конкретной задаче по расчёту параметров электротехнических установок вопрос об оптимальном значении сопротивления полезной нагрузки решается с учётом того, что является приоритетным - повышение КПД установки или увеличение её полезной мощности. Описание методики эксперимента. В лабораторной работе экспериментально определяется зависимость полезной мощности и КПД источника тока от величины сопротивления внешней нагрузки: Ра(R) h(R). Схема лабораторной установки приведена на рис.1. В качестве источника тока используется либо аккумуляторная батарея, либо выпрямляющее устройство. Эти источники тока имеют очень малое внутреннее сопротивление, соизмеримое с сопротивлением соединительных проводов. Поэтому с целью уменьшения погрешности измерения внутреннее сопротивление источника тока искусственно увеличивают, присоединяя к нему последовательно эталонное сопротивление r¢, которое по существу и является внутренним сопротивлением источника. В качестве внешней нагрузки используется магазин сопротивлений М. Сила тока измеряется с помощью амперметра А. Изменяя сопротивление нагрузки R, измеряют силу тока I. По формуле: Ра = I2R. (3) рассчитывают полезную мощность источника тока и строят график зависимости Ра(R), по которому определяют внутреннее сопротивление r источника тока. Зная внутреннее сопротивление r по формуле: h = рассчитывают КПД источника тока и строят график зависимости h(R). Сравнение графиков Ра(R) и h(R) позволяет определить оптимальное значение внешней нагрузки, при котором КПД будет составлять не менее 70%, а полезная мощность будет достаточно высокой. Результаты измерений: R, Ом 200 300 400 500 600 700 I, мА 6,6 5,6 4,8 4,2 3,8 3,5 P, мВт 78,1 94,1 92,1 88,2 86,6 85,7 h,% 40 50 57 62 67 70 Из графика Ра(R) следует, что r=300 Ом. Вывод: При использовании источника тока с внутренним сопротивлением r=300 Ом, сопротивление внешней нагрузки R=700 Ом обеспечивает КПДh= 70% при том, что полезная мощность составляет 91,1% (85,7мВт / 94,1мВт = =0,911) от максимально возможного её значения. Лабораторная работа №10-Э ОПРЕДЕЛЕНИЕ УСЛОВИЙ ЭКОНОМИЧНОГО ИСПОЛЬЗОВАНИЯ ИСТОЧНИКА ТОКА Цель работы - экспериментальная проверка теоретических выводов о наиболее экономичном использовании энергии источника тока. Теоретический анализ проблемы. Экономичное использование источника тока предусматривает создание таких условий, при которых будут достаточно высокими, с одной стороны - полезная мощность, а с другой стороны - коэффициент полезного действия. Теоретический расчёт показывает, что совместить эти два требования практически не возможно, а можно только обеспечить оптимальное соотношение для этих двух параметров. Действительно, простой расчёт показывает, что мощность Ра, выделяемая источником тока с ЭДС e во внешней цепи, то есть полезная мощность, будет максимальной, если сопротивление R внешней нагрузки равно внутреннему сопротивлению r источника тока: Ра = I2R = e2 Максимальное значение полезной мощности равно: Раmax = Коэффициент полезного действия (КПД) по определению равен: h = где Р = I2(R+r) - полная мощность, выделяемая источником тока. При R=r КПД равен: h = 50%. Остальные 50% мощности выделяются внутри источника тока, что приводит к большим потерям энергии на бесполезный разогрев источника тока, перегреву его внутренних частей и выходу источника тока из строя. Понятно, что повышения КПД источников тока является важнейшим требованием при эксплуатации силовых электрических установок. Чем меньше внутреннее сопротивление источника тока, тем выше его КПД. Таким образом, при R > r полезная мощность по абсолютному значению хотя и уменьшается, но её доля в полной мощности, выделяемой источником тока, возрастает, что экономически оказывается более выгодным. Однако, повышение КПД ограничивается тем, что, например, уже при R=5r и h = 83%, полезная мощность составляет всего 55% от максимально возможного значения (при R=r). А в пределе при R ® ¥, хотя КПД h ® 1, что очень выгодно, но вся мощность при этом выделяется внутри источника тока, а полезная мощность Ра® 0, что, естественно, не допустимо. Таким образом, в каждой конкретной задаче по расчёту параметров электротехнических установок вопрос об оптимальном значении сопротивления полезной нагрузки решается с учётом того, что является приоритетным - повышение КПД установки или увеличение её полезной мощности. Описание методики эксперимента. В лабораторной работе экспериментально определяется зависимость полезной мощности и КПД источника тока от величины сопротивления внешней нагрузки: Ра(R) h(R). Схема лабораторной установки приведена на рис.1. В качестве источника тока используется либо аккумуляторная батарея, либо выпрямляющее устройство. Эти источники тока имеют очень малое внутреннее сопротивление, соизмеримое с сопротивлением соединительных проводов. Поэтому с целью уменьшения погрешности измерения внутреннее сопротивление источника тока искусственно увеличивают, присоединяя к нему последовательно эталонное сопротивление r¢, которое по существу и является внутренним сопротивлением источника. В качестве внешней нагрузки используется магазин сопротивлений М. Сила тока измеряется с помощью амперметра А. Изменяя сопротивление нагрузки R, измеряют силу тока I. По формуле: Ра = I2R. (3) рассчитывают полезную мощность источника тока и строят график зависимости Ра(R), по которому определяют внутреннее сопротивление r источника тока. Зная внутреннее сопротивление r по формуле: h = рассчитывают КПД источника тока и строят график зависимости h(R). Сравнение графиков Ра(R) и h(R) позволяет определить оптимальное значение внешней нагрузки, при котором КПД будет составлять не менее 70%, а полезная мощность будет достаточно высокой. Результаты измерений: R, Ом I, мА P, мВт h,% vunivere.ru Если магазин МСР-63,т.е. внешнее сопротивление, отключен от источника тока, то какую величину измеряет вольтметр, подключенный к источнику ? 5********************************************************************* Электродвижущую силу Напряжение на зажимах* Напряжение на внутреннем сопротивлении Силу тока ********************************************************************** Цифровой вольтметр имеет очень большое сопротивление. Можно ли счи- тать, что при его подсоединении к зажимам источника вместо внешнего сопротивления, он покажет чему равна ЭДС ? 5********************************************************************** Да* Нет *********************************************************************** Формулы мощностей имеют вид : P2=I*I*Rвн , P1=I*U , P=I*E. Как они называются ? 5********************************************************************* Мощность потерь,полезная мощность, полная мощность* Полезная мощность, полная мощность, мощность потерь Полная мощность, мощность потерь, полезная мощность ********************************************************************** Какой вид имеют графики полной, полезной и мощности потерь в зависи- мости от тока ? 5********************************************************************** Паpаболический,линейный, параболический Линейный, параболический,паpаболический* Параболический, параболический, линейный ********************************************************************** При каком соотношении внешнего R и внутреннего Rвн сопротивлений во внешней цепи выделяется максимальная полезная мощность ? 5********************************************************************* R>Rвн R<Rвн R=Rвн* ********************************************************************** Какой вид имеет график зависимости КПД от тока ? 5********************************************************************** Линейный с отрицательным наклоном* Линейный с положительным наклоном Нелинейный *********************************************************************** Чему равен КПД, если полезная мощность максимальна ? 5*********************************************************************** 0% 50%* 100% 25% ********************************************************************** График напpяжения пересекает ось напряжений в точке 1 В и ось тока в точке 1 А.Чему равно внутреннее сопротивление Rвн источника тока ? 20*********************************************************************** 4 Ом 3 Ом 2 Ом 1 Ом* ********************************************************************** Полезная мощность максимальна при токе 0,5 А. Внутреннее сопротивление Rвн равно 1 Ом. Чему равна эта полезная мощность ? 20********************************************************************** 1 Вт 0,5 Вт 0,25 Вт* 0,75 Вт ********************************************************************** Полезная мощность максимальна при токе 0,5 А. Внутреннее сопротивление Rвн равно 1 Ом. Чему равно напряжение на зажимах ? 20********************************************************************** 1 В 0,5 В* 0,25 В 0,75 В 1,25 В ********************************************************************** Можно ли от источника тока отбирать энергию с КПД 100% ? 5********************************************************************* Да Нет* ********************************************************************** При максимуме полезной мощности полезная мощность равна 10******************************************************************** половине полной мощности* полной мощности половине потерь мощности внутри источника ********************************************************************** Каково по величине внутреннее сопротивление аккумулятора? 10******************************************************************** десятки Ом единицы Ом сотые доли Ом* ********************************************************************** Потеря мощности внутри источника равна 10******************************************************************** I^2 * R I^2 * r* E*I - I^2 * r ********************************************************************** Коэффициентом полезного действия источника называется отношение 10******************************************************************** полной мощности источника к его полезной мощности полезной мощности источника к потерям мощности внутри источника полезной мощности источника к его полной мощности* ********************************************************************** ЭДС батареи численно равна 10******************************************************************** работе по перемещению единицы заряда по всей цепи* работе по перемещению единицы заряда на внешнем участке цепи силе, действующей на единицу заряда ********************************************************************* Полезной мощностью является мощность, развиваемая источником во 10******************************************************************* внутренней цепи всей цепи внешней цепи* ********************************************************************* График зависимости U = f(I) для некоторой цепи представляет собой прямую, пересекающую ось U при значении 2.2 В , а ось I - при 10 A. Определить (в указанной последовательности): ЭДС источника, ток ко- роткого замыкания, внутреннее сопротивление источника и внешнее со- противление цепи - для получения максимальной полезной мощности. 15******************************************************************* 2.0 В; 10 A; 0.2 Om; 0.4 Om 0.22 В; 1 A; 2.2 Om; 0.22 Om 2.2 В; 10 A; 0.22 Om; 0.22 Om* ********************************************************************* Чтобы определить, является ли полезная мощность максимальной, при значении силы тока Iм = Е / 2*r , необходимо вычислить 15******************************************************************* первую производную от Р1 по I* вторую производную от Р2 по I вторую производную от Р1 по I ********************************************************************* Чему равна сила тока в цепи при "коротком замыкании" ? 10******************************************************************* E / R E / 2*r Е / r* ********************************************************************* Чему pавно максимальное значение полезной мощности для источника с ЭДС Е=4О В и внутpенним сопpотивлением r=5 Ом? 15******************************************************************** 2О Вт 80 Вт* 16О Вт 32О Вт ************************************************************************ Внутpеннее сопpотивление источника 2 Ом. Пpи каком значении внешнего сопpотивления R (Ом) полезная мощность будет pавна мощности потеpь? 1О********************************************************************** 0 1 2* 4 бесконечном *********************************************************************** Пpи каком токе вся энеpгия электp. тока в цепи идет на pазогpев источника? 5*********************************************************************** пpи I = 0 пpи I -> к бесконечности пpи I = Iк/2 пpи I = Iк* ************************************************************************* studfiles.netИзучение зависимости мощности и КПД источника тока от величины нагрузки. При какой величине внешнего сопротивления цепи полезная мощность источника тока максимальна
ЛР6
Лабораторная работа № 312 Лабораторная работа №312
При этом токе полнаямощность становится наибольшей
ЛАБОРАТОРНАЯ РАБОТА № 6
Изучение зависимости мощности и КПД источника тока от величины нагрузки
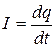 . (8.1)
. (8.1) , (8.2)
, (8.2)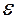 , действующей в замкнутой цепи или на ее участке. Следовательно, если работа сторонних сил по перемещению заряда dq по электрической цепи равна dАстор., то, по определению:
, действующей в замкнутой цепи или на ее участке. Следовательно, если работа сторонних сил по перемещению заряда dq по электрической цепи равна dАстор., то, по определению: . (8.3)
. (8.3)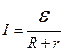 , (8.4)
, (8.4) . (8.5)
. (8.5) (8.6)
(8.6) . (8.7)
. (8.7)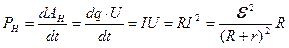 . (8.8)
. (8.8)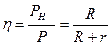 . (8.9)
. (8.9) , (8.10)
, (8.10) .
.Fizika_Kollokvium (Фомичев А.В) / Лабораторки / Лаб.№15
Определение условий экономичного использования источника тока (Раздел дисциплины "Электричество и магнетизм")
 ; Ра = Раmax при
; Ра = Раmax при  =0 или при R = r.
=0 или при R = r. . (1)
. (1) =
=  =
=  =
=  , (2)
, (2) 
 (4)
(4)  ; Ра = Раmax при
; Ра = Раmax при  =0 или при R = r.
=0 или при R = r. . (1)
. (1) =
=  =
=  =
=  , (2)
, (2) 
 (4)
(4) 
 Из графика Ра(R) следует, что r= … Ом.
Из графика Ра(R) следует, что r= … Ом.

 При использовании источника тока с внутренним сопротивлением r= … Ом, сопротивление внешней нагрузки R= … Ом обеспечивает КПДh= 70% при том, что полезная мощность составляет …% от максимально возможного её значения.
При использовании источника тока с внутренним сопротивлением r= … Ом, сопротивление внешней нагрузки R= … Ом обеспечивает КПДh= 70% при том, что полезная мощность составляет …% от максимально возможного её значения. 
26
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: