laborat / 3.3Электродвижущая сила источника. Эдс через мощность

17. Резонанс и частотные характеристики параллельного контура.

Синусоидальные ЭДС, напряжения и токи. Действующие и средние значения периодических ЭДС.

В линейной электрической цепи при действии ЭДС и (или) источника тока с одинаковым периодом T спустя некоторое время во всех участках цепи установятся периодические токи и напряжения с тем же периодом T. Величина, обратная периоду- циклическая частота Гц.

Периодические напряжения, токи ЭДС, являющиеся синусоидальнымифункциями от времени:, где e,u,i- мгновенные значения,=2pi/T-угловая частота,- начальная фаза.

О значениях периодических величин судят по их средним квадратическим значениям за период - действующимзначениям E, U, I.

-среднеезначение.

Источники ЭДС и тока. Мощности источников энергии.

Идеальный источник ЭДСпредставляет собой активный элемент с двумя выводами, напряжение на которых не зависит от тока, проходящего через источник. Работа, затрачиваемая сторонними силами на перемещение единицы положительного заряда от вывода «-» к выводу «+», называется ЭДС источника e(t). Внутреннее сопротивление такого источника 0.

Активная мощность, вырабатываемая источником ЭДС, определяется следующим образом P=UI=EI.

Идеальный источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его выводах. Предполагается, что внутреннее сопротивление такого источника бесконечно велико, поэтому параметры внешней цепи не влияют на ток источника.

Выражение законов Ома и Кирхгофа в комплексной форме.

При расчете токов в схеме с одним источником энергии, схема сворачивается к простой эквивалентной (Zэкв), затем определяется общий ток по закону Ома, токи в остальных ветвях найти по закону Кирхгофа или чужому сопротивлению. -закон Ома в комплексной форме.- чужое сопротивление.

Законы Кирхгофаприменяются для расчета цепей любой сложности. Алгоритм:

Определяется число ветвей с неизвестными токами.
Выбирается положительное направление токов в ветвях.
Определяются и обозначаются узлы в схеме. Для узлов записываетсяI закон Кирхгофа
Определяется число независимых контуров. (. Выбираются эти контуры и задается направление обхода. Для этих контуров записываетсяII закон Кирхгофа

Метод узловых напряжений. Частные случаи.

В методе узловых потенциаловсначала находятся неизвестные потенциалы узлов, затем по обобщенному закону Ома - искомые токи в ветвях.

В рассматриваемой ветви примем потенциал одного из узлов за 0. Запишем уравнения по I зак. Кирхг. для оставшихся узлов схемы. Выразим токи в ветвях согласно закону Ома (через проводимость и разность потенциалов). Полученные выражения подстав. в уравнения для I зак. В каноническом виде получим уравнения вида .

Алгоритм:

Определяется число узлов схемы. Потенциал одного принимается за 0.
Для узлов записываются уравнения. Вычисляются собственные и общие проводимости, узловые токи, потенциалы узлов.
Задаются положительными направлениями токов в ветвях. По обобщенному закону Ома вычисляются токи

Частные случаи:

Схемы с особыми ветвями

Если в цепи имеются ветви с идеальными источниками ЭДС и сопротивлениями этих ветвей можно пренебречь, то целесообразно принять в заданной схеме потенциал «конца» ветви с идеальным источником ЭДС за 0, тогда потенциал начала равен ЭДС. Ток в особой ветви определяется по закону Кирхгофа.

Схемы в двумя узлами

Потенциал одного из узлов принимается за 0, используется формула «двух узлов»

Синусоидальный ток в цепи с параллельным соединением участков.

Пусть к цепи с параллельным соединением элементов приложено напряжение . По первому закону Кирхгофа. При параллельном соединении на всех элементах напряжение одинаково,U=. По закону Ома находится ток в каждой ветви. Ток в резисторе совпадает по фазе с напряжением, в индуктивности – отстает на, ток в емкости – опережает на.

Применение законов Кирхгофа для расчета сложных цепей. Алгоритм метода.

Законы Кирхгофаприменяются для расчета цепей любой сложности. Алгоритм:

Определяется число ветвей с неизвестными токами.
Выбирается положительное направление токов в ветвях.
Определяются и обозначаются узлы в схеме. Для узлов записываетсяI закон Кирхгофа
Определяется число независимых контуров. (. Выбираются эти контуры и задается направление обхода. Для этих контуров записываетсяII закон Кирхгофа

Изображение синусоидальных функций времени векторами и комплексными числами.

Пусть некоторая величина u изменяется по синусоидальному закону . Возьмем прямоуг. сист. осей N0M. Расположим под угломотносительно горизонт. оси 0М вектор, длина которого в выбранном масштабе равна. Представим, что векторс моментаt=0 начинает вращаться вокруг начала координат 0 против ч.с. с постоянной угловой скоростью. В момент времени t вектор составит с осью 0М угол. Его проекция на ось NN' равна в выбранном масштабе мгновенному значению рассматриваемой величины u ().

Вектор – вектор, изображающий синусоидальную функцию времени, вектор величины u. Он соответствует комплексному числу, модуль которого равен, а аргумент – углу.- комплексная амплитуда. Ее можно записать в полярной, показательной, тригонометрической и алгебраической формах.

, где,.

Пусть задана полярная форма записи числа .. Если задана комплексная форма записи, то,.

Принцип наложения и основанный на нем метод расчета.

Принцип наложения позволяет расчленить сложную задачу на ряд более простых, в каждой рассматриваемой цепи действует только одна ЭДС или источник тока. Все остальные источники предполагаются отсутствующими: источники ЭДС должны быть замкнуты накоротко с сохранением в ветвях их внутренних сопротивлений, источники тока должны быть разомкнуты, но их внутренние проводимости сохраняются в соответствующих ветвях.

Алгоритм:

Определяется число источников энергии. Источники ЭДС замыкаются, источники тока-размыкаются.
Расчитываются каждые полученные схемы по отдельности.
Токи в ветвях исходной схемы равны алгебраическим суммам токов в частых схемах.

Преобразование электрических схем.

Преобразование источника ЭДС в источник тока и наоборот.

При заданных ,,, и наоборот,

Преобразование параллельного соединения ветвей с источниками ЭДС и тока.

Каждая группа параллельных ветвей заменяется одним источником с эквивалентным ЭДС и эквивалентным внутренним сопротивлением. ,

Преобразование треугольника в звезду и звезды в треугольник.

При известных сопротивлениях сторон треугольника, сопротивления лучей звезды находятся следующим образом:

По известным сопротивлениям лучей звезды сопротивления сторон треугольника находятся

Резонанс и частотные характеристики неразветвленной цепи.

Резонанс - такой режим пассивной цепи, содержащей катушки индуктивности и конденсаторы, при котором ее входное реактивное сопротивление или входная реактивная проводимость равны 0. При резонансе ток на входе цепи совпадает по фазе с напряжением (или =0).

Условие резонанса в последовательном контуре (резонанс напряжений) wL=1/wC. Значения, при которых наступает резонанс:.- резонансная частота.

Добротность контура показывает, во сколько раз напряжение на реактивных элементах при резонансе больше входного напряжения.

Условия передачи максимальной мощности источника энергии к приемнику.

Приемник получает от источника наибольшую активную мощность, когда его комплексное сопротивление является сопряженным с комплексным внутренним сопротивлением источника.

, при любом R мощность достигает наибольшей величины, когда. Тогда. Исследуем функцию P на экстремум, получим. При соблюдении этого условия приемник потребляет мощность Pmax=.

Метод эквивалентного генератора.

Ток в любой ветви mn линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником ЭДС, которая должна быть равна напряжению на выводах разомкнутой ветви mn, а внутреннее сопротивление источника должно равняться входному сопротивлению пассивной электрической цепи со стороны выводов m и n при разомкнутой ветви mn.

Ток в ветви mn ,– внутреннее сопротивление пассивного двухполюсника, полученное после того, как все ЭДС замкнуты накоротко, а источники тока разомкнуты.

Алгоритм:

Выделим ветвь mn, в которой определим ток , остальная часть схемы - активный двухполюсник.
В ветвь mn включим две равные и противоположно направленные ЭДС ,равно напряжению между выводами m и n при разомкнутой ветви mn. При этом токв ветви mn не изменится. По принципу наложения ток находится как алгебраическая сумма токов, создаваемых каждым источником. Но все источники внутри активного двухполюсника совместно сне вызовут тока. Поэтому ток в схеме с пассивным двухполюсником будет равен действительному току в ветви mn.

,относят к активному двухполюснику, тогда.,- ток в ветви mn при.

Применение метода контурных токов для расчета сложных цепей. Алгоритм метода.

Для расчета сложной цепи можно ограничиться совместным решением (уравнений, составленных по II закону Кирхгофа методом контурных токов.

Алгоритм:

Определяется число независимых контуров и задаются направления контурных токов (.
Для контурных токов составляется система уравнений по II закону Кирхгофа. Находятся токи.
Задаются направления токов в ветвях, находятся искомые токи по I закону Кирхгофа или анализу схемы.

Мощность цепи синусоидального тока.

Пусть напряжение и ток на входе пассивного двухполюсника изменяются по синусоидальному закону. Мгновенная мощность, производимая и отдаваемая источником ЭДС и потребляемая двухполюсником, равна скорости совершения работы в данный момент времени

Мгновенная мощность может быть + и -. Когда мгновенная мощность -, энергия не поступает в двухполюсник, возвращается от двухполюсника к источнику ЭДС.

Активная мощность- среднее значение мгновенной мощности за период

Полная мощностьравна произведению действующих значений напряжений и тока S=UI.

При расчете цепей синусоидального тока используется реактивная мощностьQ=UIsinϕ.

Комплексная мощность . Модуль комплексной формы равен полной мощности, а аргумент равен углу сдвига фаз между напряжением и током.

Комплексное, полное, активное, реактивное сопротивления цепи. Разность фаз напряжений и тока.

=.-комплексноесопротивление,z=U/I=Um/Im-полноесопротивление, равно модулю комплексного сопротивления,.

, -действительная (активная)часть,-мнимая (реактивная).

,,. Ток в резисторе совпадает по фазе с напряжением, в индуктивности – отстает на, ток в емкости – опережает на.

Элементы электрических цепей. Связи между напряжением и током в основных элементах цепи.

Резистивные элементыс сопротивлением R,r входят в схему для учета необратимого преобразования электромагнитной энергии в другие виды энергии и для учета энергии излучения. Напряжение на выводах резистора и ток в нем связаны законом Ома. Обратная величина называется проводимостью.

Индуктивный элементс индуктивностью L учитывает энергию магнитного поляи явление самоиндукции.

Конденсаторс емкостью C учитывает энергию магнитного поля

Резонанс это режим работы пассивной цепи с катушкой индук. и конденсат при котором ее входное реактивное сопротивл=0 Z=R+jXL-JXc=R+jwL+1/jwC=X=wL-1/wC

Условием резонанса при паралель. соед RLCтакже является отсутствие сдвига фаз между током и напряжением на зажимах цепи. Резонанса при паралельном соед. можно добится изменением либо частоты, либо индук. либо емкости. При резонансе реактивная проводимость цепи равна нулю и полная проводимость цепи достигает минимального значения поэтому ток в общей цепиI=UGТоки в катушке и конденсаторе могут превосходить, а иногда намного , суммарный ток в цепи, поэтому резонанс при паралельном соед. называютрезонансом токов.

Частотные хар-ки графики с страниц 308-309 синего учебника, авт. Демирчян

18. Трансформатор без стального сердечника. Схема, уравнения, векторные диаграммы.

"воздушный трансформатор" - транс. состоящий из 2-х или более индуктивн. связанных катушек, не запаянных на общий стержень. Такие трансформаторы применяются в устройствах автоматики, измерит. техники и связи, электрическая схема замещения такого транса имеет вид

Zн=Rн+-jXнZн=0Zн= бескон. (xx)

Для анализа схемы введем обозначения wL1=X1R2+Rн=R22wL2+Хн=Х22

Второй з. Кирх. для первич. и вторич. контура имеет вид I1*R+I1*jX1-I2*jwM=U

I2*R22+I2*X22-I1jwM=0

гальванически соед. две обмотки (---) режим работы транса при этом не изменится, для полученной схемы можем применить развязку индук. свзяи.

Идеальный транс-это транс в котором, при любых сопротивл. нагрузки, отношение первич и вторич. комплексных напряжений и отношений вторич и первич токов равны друг другу и равны пост. числу, назыв. коэффициентом трансформации, идеального транса n=U1/U2=I2/I1

Идеальн. транс. между нагрузкой и ист. энергии изменяет сопротив. нагрузки пропорционально квадрату коэф. трансформации, это св-во исп. для выравнивания сопротивл. ист. и нагрузки.

-предположим что I2=I1<0*

-отложим ток1

-обойдем вторичный контур трансформатора

-UR2совпадает по фазе с током

-URн совпадает

-UL2 опережает на п/2

из конца UL2 в начало координат проведем векторI1jXm

-получили вторичную диаграмму вторичного контура

напряжение взаимной индукции I1jXmопережает ток1 на угол п/2, переносим его в начало координат

Перейдем к векторной диаграмме первого контура

Ur1

UL1-опережает ток1 на п/2

Um1=I2jXmопережает ток2 на п/2

соеденим конец вектора I2jXmcначалом

19. Расчет симметричных режимов 3хфазной цепи

Симетр. звездаПредположим что в схеме известно Uф или Uл, сопротивление нагрузки. найти токи.

При симметричной нагрузке генератора 0 и нагрузки 01 имеют одинаковый потенциал, поэтому не нарушая работ схемы, можно их закоротить. В полученных 3-х схемах все оди-

накого но Uф отличается на 120* поэтому достаточно выделить одну фазу, и вычеслить ток, а токи в остальных фазах +-120*

где Ua=Uф<0* если дано линейное то сначала его нужно вычеслить фазноеUф=Uл/корень из 3, по закону Ома вычеслим токIa=Ua/Za, гдеZaфазное сопротивление. Линейные(фазные) токи найдем поворотом на 120*Iв=Ia<-120*Ic=Ia<+120*

Треугольник

Zав=Zвс=Zса=Zпри соединении треугольникомUф=Uл, при заданном числовом знач. и извест. фазным сопротивлениям, по з.Ома найдем ток в фазе АВIав=Uав/Zав=Uа<30*/Zав

остальные фазные токи найдем поворотом на 120* РАСПИСАТЬ САМОМУ. линейные токи можно определять по 1з.Кирхгофа (Iа=Iав-Iас) разность фазных токов. Но для симметричных цепей можно воспользоваться формулойIa=корень(3)*Iав<-30*, другие поворотом на 120* Векторная диаграмма для чисто активной фазной нагрузки (фазные токи строим совпадающими с напряжением

studfiles.net

Электродвижущая сила

«Физика - 10 класс»

Любой источник тока характеризуется электродвижущей силой, или сокращённо ЭДС. Так, на круглой батарейке для карманного фонарика написано: 1,5 В. Что это значит?

Если соединить проводником два разноимённо заряженных шарика, то заряды быстро нейтрализуют друг друга, потенциалы шариков станут одинаковыми, и электрическое поле исчезнет (рис. 15.9, а).

Сторонние силы.

Для того чтобы ток был постоянным, надо поддерживать постоянное напряжение между шариками. Для этого необходимо устройство (источник тока), которое перемещало бы заряды от одного шарика к другому в направлении, противоположном направлению сил, действующих на эти заряды со стороны электрического поля шариков. В таком устройстве на заряды, кроме электрических сил, должны действовать силы неэлектростатического происхождения (рис. 15.9, б). Одно лишь электрическое поле заряженных частиц (кулоновское поле) не способно поддерживать постоянный ток в цепи.

Любые силы, действующие на электрически заряженные частицы, за исключением сил электростатического происхождения (т. е. кулоновских), называют сторонними силами.

Вывод о необходимости сторонних сил для поддержания постоянного тока в цепи станет ещё очевиднее, если обратиться к закону сохранения энергии.

Электростатическое поле потенциально. Работа этого поля при перемещении в нём заряженных частиц по замкнутой электрической цепи равна нулю. Прохождение же тока по проводникам сопровождается выделением энергии — проводник нагревается. Следовательно, в цепи должен быть какой-то источник энергии, поставляющий её в цепь. В нём, помимо кулоновских сил, обязательно должны действовать сторонние, непотенциальные силы. Работа этих сил вдоль замкнутого контура должна быть отлична от нуля.

Именно в процессе совершения работы этими силами заряженные частицы приобретают внутри источника тока энергию и отдают её затем проводникам электрической цепи.

Сторонние силы приводят в движение заряженные частицы внутри всех источников тока: в генераторах на электростанциях, в гальванических элементах, аккумуляторах и т. д.

При замыкании цепи создаётся электрическое поле во всех проводниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны от положительно заряженного электрода к отрицательному), а во внешней цепи их приводит в движение электрическое поле (см. рис. 15.9, б).

Природа сторонних сил.

Природа сторонних сил может быть разнообразной. В генераторах электростанций сторонние силы — это силы, действующие со стороны магнитного поля на электроны в движущемся проводнике.

В гальваническом элементе, например в элементе Вольта, действуют химические силы.

Элемент Вольта состоит из цинкового и медного электродов, помещённых в раствор серной кислоты. Химические силы вызывают растворение цинка в кислоте. В раствор переходят положительно заряженные ионы цинка, а сам цинковый электрод при этом заряжается отрицательно. (Медь очень мало растворяется в серной кислоте.) Между цинковым и медным электродами появляется разность потенциалов, которая и обусловливает ток во внешней электрической цепи.

Электродвижущая сила.

Действие сторонних сил характеризуется важной физической величиной, называемой электродвижущей силой (сокращённо ЭДС).

Электродвижущая сила источника тока равна отношению работы сторонних сил при перемещении заряда по замкнутому контуру к абсолютной величине этого заряда:

Электродвижущую силу, как и напряжение, выражают в вольтах.

Разность потенциалов на клеммах батареи при разомкнутой цепи равна электродвижущей силе. ЭДС одного элемента батареи обычно 1—2 В.

Можно говорить также об электродвижущей силе и на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всём контуре, а только на данном участке.

Электродвижущая сила гальванического элемента есть величина, численно равная работе сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому.

Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории перемещения зарядов.

Источник: «Физика - 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы постоянного тока - Физика, учебник для 10 класса - Класс!ная физика

Электрический ток. Сила тока --- Закон Ома для участка цепи. Сопротивление --- Электрические цепи. Последовательное и параллельное соединения проводников --- Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» --- Работа и мощность постоянного тока --- Электродвижущая сила --- Закон Ома для полной цепи --- Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Устали? - Отдыхаем!

Вверх

class-fizika.ru

3.3Электродвижущая сила источника

Учреждение образования

«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ ИСТОЧНИКА ТОКА МЕТОДОМ КОМПЕНСАЦИИ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №3.3

по дисциплине

«ФИЗИКА»

для студентов всех специальностей

Минск 2006

ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДВИЖУЩЕЙ СИЛЫ ИСТОЧНИКА ТОКА МЕТОДОМ КОМПЕНСАЦИИ

ЦЕЛЬ РАБОТЫ

Определить ЭДС не менее трех неизвестных источников.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1. Набор источников тока.

2. Нормальный элемент.

3. Реохорд.

4. Гальванометр.

5. Переключатели.

ЭЛЕМЕНТЫ ТЕОРИИ

Условием движения электрических зарядов в проводнике является наличие в нем электрического поля, которое создается и поддерживается особыми устройствами, получившими название источников тока.

Основной величиной, характеризующей источник тока, является его электродвижущая сила. Электродвижущей силой источника (сокращенно ЭДС) называется скалярная физическая величина – количественная мера способности источника создавать на его зажимах (полюсах) разность потенциалов. Она равна работе сторонних сил по перемещению заряженной частицы с положительным единичным зарядом от одного полюса источника к другому, т.е.

. (1)

В СИ ЭДС измеряется в вольтах (В), т.е. в тех же единицах, что и напряжение.

Сторонние силы источника – это силы, которые осуществляют разделение зарядов в источнике и тем самым создают на его полюсах разность потенциалов. Эти силы могут иметь различную природу, но только не электрическую (отсюда и название).

Если электрическую цепь разделить на два участка – внешний, с сопротивлением R, и внутренний, с сопротивлением r, то ЭДС источника тока окажется равной сумме напряжений на внешнем и внутреннем участках цепи:

. (2)

По закону Ома напряжение на любом участке цепи определяется величиной протекающего тока и его сопротивлением:

Так как , следовательно

, (3)

т.е. напряжение на полюсах источника при замкнутой цепи зависит от соотношения сопротивлений внутреннего и внешнего участков цепи. Если , то приблизительно равно U. На этом основано приблизительное определение ЭДС при помощи вольтметра с большим сопротивлением, подключаемого к полюсам источника. Только в отсутствие тока в источнике его ЭДС будет равна напряжению на полюсах.

Величину ЭДС можно определить точно электростатическим или компенсационным методом. При измерении ЭДС электростатическим методом цепь остается разомкнутой, т.к. измерение разности потенциалов на полюсах источника проводится прибором, не потребляющим тока (электрометр, электростатический вольтметр). При измерении ЭДС компенсационным методом цепь источника замкнута, но необходимые отсчеты делаются в моменты отсутствия тока в источнике.

Компенсационный метод определения ЭДС

Сущность метода компенсации в измерении ЭДС заключается в подборе и определении напряжения на участке электростатической цепи, равного ЭДС исследуемого источника.

Схема электрической цепи для определения ЭДС методом компенсации изображена на рис.1.

Два источника ЭДС  и x включены навстречу друг другу. Сопротивления R1 и R2 выполнены в виде однородной проволоки, натягиваемой между точками А и В, а точка С определяется скользящим контактом (при необходимости очень высокой точности измерений R1 и R2 представляют собой магазины сопротивлений).

Выберем положительные направления токов, как показано на рис.1, и применим к рассматриваемой схеме правила Кирхгофа. Первое правило для точек А и С дает

(4)

Второе правило для контуров АBCA и АxСА приводит к уравнениям:

(5)

(6)

Эти уравнения вполне определяют все неизвестные токи. Однако мы ограничимся частным случаем и предположим, что сопротивления R1 и R2 подобраны таким образом, что ток Ixв цепи гальванометра G равен 0. В этом случае уравнения (4)-(6) принимают вид

Из двух последних уравнений находим

, (7)

где R – полное сопротивление струны, которое не зависит от положения скользящего контакта С.

Предположим теперь, что вместо источника с неизвестной ЭДС x мы включили в схему другой источник н с известной ЭДС и перемещением контакта С, а следовательно, изменением переменных сопротивлений, вновь добились компенсации (I1=0). Для этого вместо сопротивления rx потребовалось ввести сопротивление rн. Тогда

. (8)

Разделив почленно (7) на (8), получим

. (9)

Это равенство и лежит в основе сравнения ЭДС методом компенсации.

Отметим, что отношение сравниваемых ЭДС не зависит от внутренних сопротивлений источников и от других сопротивлений схемы, а определяется только отношением сопротивлений участка цепи, к которому поочередно подключают сравниваемые источники ЭДС. Не требуется знать и ЭДС вспомогательного источника , которая только должна быть достаточно постоянна во время измерения и больше обеих сравниваемых ЭДС и .

МЕТОДИКА ЭКСПЕРИМЕНТА И ОПИСАНИЕ УСТАНОВКИ

ЭДС гальванического элемента в данной работе определяется путем ее сравнения с ЭДС нормального элемента =1,00 В. Напряжение между электродами этого и подобных ему других нормальных элементов весьма постоянно. Поэтому они играют в электрической измерительной технике ту же роль, что и эталоны длины (метр) и массы (килограмм) при измерении механических величин.

Схема соединения приборов изображена на рис.2, где  - вспомогательный источник питания; АВ – струна реохорда со скользящим контактом С; и – нормальный и исследуемый элементы; G – гальванометр; П – двухполюсный переключатель; К – ключ, замыкающий цепь вспомогательного источника питания.

Решение равенства (9) относительно позволяет получить формулу для вычисления ЭДС исследуемого элемента

(10)

Струна АВ является однородным проводником постоянного сечения.

Сопротивления ее участков цепи R1иR1н (длиной lx и lн соответственно), входящих в (10), можно выразить как

R1 и R1н =.

Подставляя эти значения в (10) , окончательно получаем расчетную формулу для определения ЭДС исследуемого источника тока

. (11)

Как видим, в этой формуле отношение сопротивлений участков струны равно отношению их соответствующих длин.

Метод компенсации практически можно осуществить при следующих условиях:

ЭДС основного источника должна быть больше ЭДС как эталонного, так и исследуемого элементов;

2) цепь следует замыкать на малые промежутки времени, достаточные для фиксирования наличия или отсутствия тока в гальванометре.

Порядок выполнения работы

1. Собрать схему, изображенную на рис.2 (если она собрана, убедиться в ее соответствии рисунку).

2. Включить элемент в цепь гальванометра (тумблер П в верхнем положении). Перемещая контакт С, добиться компенсации этого элемента напряжением на участке струны АС, т.е. установления «0» на гальванометре. Измерить длину участка струны lн, при которой осуществляется компенсация.

3. Включить один из пяти неизвестных элементов в цепь гальванометра (тумблер П в нижнем положении). Перемещая контакт С, добиться компенсации этого элемента напряжением на участке струны АС, о чем свидетельствует установление «0» на гальванометре. Измерить длину участка струны lх, при которой осуществляется компенсация.

4. Рассчитать ЭДС неизвестного элемента по формуле (11).

5. Повторить измерения, указанные в пунктах 2-4 еще несколько раз для получения более точных результатов. Рассчитать среднее значение ЭДС и погрешность результата. Результаты измерений и расчетов записать в таблицу 1 с обязательным указанием размерности всех используемых величин.

Таблица 1

№ элемента	№ опыта (i)	lн	lх	xi	xср	\|xi\|	
	1
1	2
	3

6. Окончательный результат записать в виде , где s ‑ среднеквадратичное отклонение, вычисляемое по формуле:

где n – число измерений для одного элемента.

7. Повторить задания 2-7 для других элементов х. Составить для них аналогичные таблицы.

Контрольные вопросы

1. Дать определение электродвижущей силе источника. Какова ее размерность?

2. Какие силы вызывают разделение зарядов в источниках питания? Привести примеры.

3. Как можно определить значение ЭДС источника?

4. Какие методы позволяют рассчитать ЭДС источника с большой степенью точности? В чем их сходство?

5. В чем сущность метода компенсации?

Вывести расчетную формулу для определения ЭДС источника методом компенсации.

Литература

1. С.Г. Калашников. Электричество. М.: «Наука», 1977 г.

2. И.Е. Иродов. Основные законы электромагнетизма. М.: «Высшая школа», 1983 г.

studfiles.net

Мощность через эдс и сопротивление

Связь между токами и напряжениями в R , L , C . Источники ЭДС и тока. Линейные и нелинейные цепи. Законы Ома и Кирхгофа. Цепи синусоидального тока. Характеристики синусоидального тока (напряжения). Угол сдвига фаз. Действующее и среднее значение. Энергия в емкости и индуктивности. Цепь с последовательным соединением R , L , C . Активные, реактивные и полные сопротивления. Активная мощность. Обмен энергией в цепи переменного тока.

Термины и определения основных понятий

Источник электрического тока – источник электрической энергии, характеризующийся электрическим током в нем и внутренней проводимостью.

Источник электрического напряжения – источник электрической энергии, характеризующийся электродвижущей силой и внутренним электрическим сопротивлением.

Активная мощность – величина, равная среднеарифметическому значению мгновенной мощности двухполюсника за период.

Синусоидальный электрический ток – периодический электрический ток, являющийся синусоидальной функцией времени.

Фаза (синусоидального электрического) тока - аргумент синусоидального электрического тока, отсчитываемый от точки перехода значения тока через нуль к положительному значению.

Теоретический материал Связь между током и напряжением в элементах r, l, c

Сопротивление ,.

Численно разность потенциалов равна работе, совершаемой электрическим полем по перемещению единичного положительного заряда из точки 1 в точку 2.

Для напряжения также, как и для тока произвольно выбираем направление, обычно она совпадает с направлением тока (рис 2.1).

- закон Ома

Индуктивность

Согласно закону электромагнитной индукции изменение потокосцепления самоиндукции вызывает ЭДС самоиндукции.

Величина

называется напряжением на индуктивности. Направлениесовпадает с направлением тока (рис.2.2).

Емкость

При изменении на пластинах конденсатора изменяется электрический заряд и, следовательно, в цепи с ёмкостью появляется электрический ток.

Условное положительное направление напряжения на ёмкости совпадает с условным положительным направлением тока (рис.2.3).

Источники эдс и тока

При расчётах электрических цепей пользуются идеализированными источниками электрической энергии – источники ЭДС и тока.

Им приписывают следующие свойства:

Источник эдс

Упорядоченное перемещение носителей электрических зарядов от « - » к « + » внутри источника происходит за счёт присущих источнику сторонних сил. Величина, численно равная работе, совершаемой сторонними силами при перемещении единичного, положительного заряда от « - » к « + » называется ЭДС источника. Стрелка внутри источника указывает на возрастание потенциала (рис.2.4).

Идеальным источником ЭДС называется активный элемент с двумя выводами, напряжение на которых не зависит от величины тока, протекающего через источник. Внутреннее сопротивление источника ЭДС равно нулю.

ЭДС и напряжение на зажимах источника одинаковы.

;

При замыкании зажимов источника ЭДС ток теоретически должен быть бесконечно большим, и, следовательно, идеальный источник ЭДС можно рассматривать как источник бесконечной мощности.

Для обозначения реального источника ЭДС используется сопротивление, включённые последовательно с идеальным источником (рис.2.5). Оно ограничивает мощность, отдаваемую во внешнюю цепь.

;

ольт-амперная характеристика, построенная по уравнению (*), называется внешней (рис. 2.6).

Источник ЭДС

Рисунок 1 - Обозначение на схемах источника ЭДС (слева) и реального источника напряжения (справа)

Источник ЭДС (идеальный источник напряжения ) - двухполюсник , напряжение на зажимах которого постоянно (не зависит от тока в цепи). Напряжение может быть задано как константа, как функция времени, либо как внешнее управляющее воздействие.

В простейшем случае напряжение определено как константа, то есть напряжение источника ЭДС постоянно.

Реальные источники напряжения

Рисунок 2

Рисунок 3 - Нагрузочная характеристика

Идеальный источник напряжения (источник ЭДС) является физической абстракцией, то есть подобное устройство не может существовать. Если допустить существование такого устройства, то электрический ток I , протекающий через него, стремился бы к бесконечности при подключении нагрузки,сопротивление R H которой стремится к нулю. Но при этом получается, что мощность источника ЭДС также стремится к бесконечности, так как . Но это невозможно, по той причине, что мощность любого источника энергии конечна.

В реальности, любой источник напряжения обладает внутренним сопротивлением r , которое имеет обратную зависимость от мощности источника. То есть, чем больше мощность, тем меньше сопротивление (при заданном неизменном напряже

zgbox.ru

Сторонние силы и ЭДС

Для того, чтобы поддерживать ток достаточно длительное время, необходимо от конца проводника с меньшим потенциалом непрерывно отводить, а к другому концу – с большим потенциалом – подводить электрические заряды. Т.е. необходим круговорот зарядов. Поэтому в замкнутой цепи, наряду с нормальным движением зарядов, должны быть участки, на которых движение (положительных) зарядов происходит в направлении возрастания потенциала, т.е. против сил электрического поля (рис. 7.3).

Рис. 7.3

Перемещение заряда на этих участках возможно лишь с помощью сил неэлектрического происхождения (сторонних сил): химические процессы, диффузия носителей заряда, вихревые электрические поля. Аналогия: насос, качающий воду в водонапорную башню, действует за счет негравитационных сил (электромотор).

Сторонние силы можно характеризовать работой, которую они совершают над перемещающимися по замкнутой цепи или ее участку зарядами.

Величина, равная работе сторонних сил по перемещению единичного положительного заряда в цепи, называется электродвижущей силой (ЭДС), действующей в цепи:

(7.4.1)

Как видно из (7.4.1), размерность ЭДС совпадает с размерностью потенциала, т.е. измеряется в вольтах.

Стороннюю силу, действующую на заряд, можно представить в виде:

(7.4.2)

– напряженность поля сторонних сил.

Работа сторонних сил на участке 1 – 2:

тогда

(7.4.3)

Для замкнутой цепи:

(7.4.4)

Циркуляция вектора напряженности сторонних сил равна ЭДС, действующей в замкнутой цепи (алгебраической сумме ЭДС).

При этом необходимо помнить, что поле сторонних сил не является потенциальным, и к нему нельзя применять термин разность потенциалов или напряжение.

ens.tpu.ru

ЭДС и напряжение источника электрической энергии

Для того чтобы разобраться что такое электродвижущая сила источника электрической энергии, необходимо вспомнить, что представляет собой электрический ток и за счёт чего происходит его движение в электрической цепи.

ЭДС источника электрической энергии Известно, электрический ток движется в цепи за счёт разницы потенциалов. Для того чтобы движение тока не прекращалось, нужно непрерывно обеспечивать эту разницу потенциалов между полюсами источника напряжения, к которому подключена цепь.

Подобное явление можно сравнить с трубкой, которая соединена с двумя резервуарами с водой. Если в этих резервуарах будет разный уровень воды, то она непременно начнёт перетекать через трубку из одного сосуда в другой и наоборот; так если разница в уровне воды между сосудами будет постоянной, то и движение воды не прекратиться.

Данный пример помогает понять, что происходит в электрической цепи. Электрическая энергия, действующая внутри источника, постоянно поддерживает электрический ток. Таким образом, обеспечивается непрерывная работа.

Понятие «Электродвижущая сила»

В данном случае, электродвижущая сила (ЭДС) – это сила, которая поддерживает разницу потенциалов на разных полюсах источника энергии, она вызывает и поддерживает движение тока, а также преодолевает внутренне сопротивление проводника и т. д.

Ток может протекать по проводнику столь же долго, сколь существует разница потенциалов. Свободные электроны приходят в постоянное движение между телами, которые соединены в электрическую цепь.

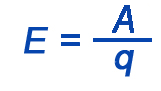Формула расчета ЭДС Электродвижущая сила – величина физическая, т. е., её можно измерить и использовать как одну из характеристик электрической цепи. В источниках постоянного, либо переменного тока ЭДС характеризует работу непотенциальных сил. Это работа сторонних или непотенциальных сил в замкнутом контуре, когда они перемещают одиночный электрический заряд вдоль всего контура.

Возникновение электродвижущей силы

Существует различные виды источников электрической энергии. Каждый из них можно охарактеризовать по-разному, у каждого вида свои принципиальные особенности. Эти особенности влияют на возникновение электродвижущей силы, причины данного явления весьма специфичны, т. е. зависят от вида источника.

В чём же главная суть различий? К примеру, если мы берём химические источники электрической энергии, такие как аккумуляторы, другие гальванические элементы, то электродвижущая сила становится результатом химической реакции. Если рассмотреть генераторы, то здесь причиной является электромагнитная индукция, а в различных термических элементах основой является тепловая энергия. От этого возникает электрический ток.

Измерение электродвижущей силы

Электродвижущая сила измеряется в вольтах, также как и напряжение. Эти величины связаны между собой. Однако ЭДС можно измерять на отдельном участке электрической цепи, тогда будут измеряться работы не всех сил, действующих на этом контуре, а только те, которые есть на отдельно взятом участке цепи.

Разность потенциалов, являющуюся причиной возникновения и прохождения тока по цепи, также можно назвать напряжением. Однако, если ЭДС – работа сторонних сил, которая совершается при перемещении единичного заряда, то она не может быть охарактеризована с помощью разницы потенциалов, т. е., напряжения, так как работа зависит от траектории движения заряда, эти силы непотенциальны. В этом различие таких понятий как напряжение и электродвижущая сила.

Данная особенность учитывается при измерении ЭДС и напряжения. В обоих случаях используют вольтметры. Для того чтобы измерить ЭДС нужно при разомкнутой внешней цепи подключить вольтметр к концам источника энергии. Если требуется измерить напряжение на выбранном участке электрической цепи, то вольтметр должен быть подключён параллельно к концам конкретного участка.

ЭДС и напряжение источника электрической энергии могут быть независимо от величины электрического тока в цепи; в разомкнутой цепи ток равен нулю. Однако если генератор или аккумулятор будут работать, то они возбуждают ЭДС, а значит, между концами возникает напряжение.

volt220.ru

ЭДС и конечное напряжение

Физика > ЭДС и конечное напряжение

Конечное напряжение (напряжение на выходе источника) основывается на электродвижущей силе и внутреннем сопротивлении.

Задача обучения

Переведите соотношение между ЭДС и конечным напряжением в формулу.

Основные пункты

Электродвижущая сила отображает разность потенциалов источника в момент, когда ток лишен движения.
Конечное напряжение – выход напряжения в устройстве, измеренное через клеммы.
Формула расчета: V = ЭДС - Ir.

Термины

Конечное напряжение – выход напряжения в устройстве, измеряемое на клеммах.
Электродвижущая сила (ЭДС) – напряжение, сформированное батареей или магнитной силой в соответствии с законом Фарадея.
Разность потенциалов – отличие в показателях потенциальной энергии между двумя точками в электрическом поле.

Если вы забудете выключить фары на машине, то со временем они потускнеют. Причина – разряд батареи. Почему же они просто не мигают при потере энергии? Постепенное затухание говорит о том, что конечное напряжение снижается по мере расхода заряда. Все дело в том, что у всех источников напряжения есть две главные части: источник электрической энергии и внутреннее сопротивление.

Электродвижущая сила

Все источники напряжения формируют разность потенциалов и могут отправлять ток при подключении к сопротивлению. Если брать небольшой масштаб, то из-за этого отличия создается электрическое поле, влияющее на заряды и вызывающее ток. Мы называем это отличие электродвижущей силой (ЭДС). Но не думайте, что перед нами «сила» в привычном понятии. Это особая разновидность разности потенциалов источника, когда ток лишен движения. Измеряется в вольтах.

ЭДС связана с источником разности потенциалов, но отличается от конечного напряжения при проходе тока. К примеру, напряжение на аккумуляторе будет меньшим, чем ЭДС. Если конечное напряжение можно вычислить без подачи тока, то оно приравнивается к ЭДС.

Конечное напряжение

Выход напряжения из устройства измеряется на клеммах и именуется конечным напряжением (V). Его вычисляют по формуле:

Любой источник напряжения обладает ЭДС, связанной с источником разности потенциалов. Также оно настраивается на сопротивление (r), связанное с конструкцией. Здесь видны выходные клеммы, по которым измеряют конечное напряжение (V). Так как V = ЭДС - Ir, конечное напряжение приравнивается к ЭДС, если ток отсутствует

V = ЭДС – Ir (r – внутреннее сопротивление, I – протекающий во время измерения ток).

I положителен, если ток течет от положительной клеммы. Чем больше ток, тем меньше конечное напряжение. Также конечное напряжение уменьшается при росте внутреннего сопротивления.

v-kosmose.com

Каталог товаров