Иметь представление о мощности при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия. Знать зависимости для определения мощности при поступательном и вращательном движениях, КПД. Уметь рассчитать мощность с учетом потерь на трение и сил инерции. Мощность Для характеристики работоспособности и быстроты совершения работы введено понятие мощности. Единицы измерения мощности: ватты, киловатты, Мощность при поступательном движении (рис. 16.1) Учитывая, что S/t = vcp, получим где F — модуль силы, действующей на тело; vср — средняя скорость движения тела. Средняя мощность при поступательном движении равна произведению модуля силы на среднюю скорость перемещения и на косинус угла между направлениями силы и скорости. Тело движется по дуге радиуса r из точки М1 в точку M2 Работа силы: где Мвр — вращающий момент. Учитывая, что где ωcp — средняя угловая скорость. Мощность силы при вращении равна произведению вращающего момента на среднюю угловую скорость. Если при выполнении работы усилие машины и скорость движения меняются, можно определить мощность в любой момент времени, зная значения усилия и скорости в данный момент. Коэффициент полезного действия Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений. Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу. Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом полезного действия (КПД): Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам: Затраченная мощность больше полезной на величину мощности, идущей на преодоление трения в звеньях машины, на утечки и тому подобные потери. Чем выше КПД, тем совершеннее машина. Примеры решения задач Решение 1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки. Полезная мощность определяется по формуле Р = Fv cos α. В данном случае α = 0; груз движется поступательно. 2. Скорость подъема груза 3. Необходимое усилие равно весу груза (равномерный подъем). 6. Полезная мощность Р = 3000 • 4 = 12 000 Вт. 7. Полная мощность. затрачиваемая мотором, Пример 2. Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления воды движению судна. КПД машины 0,4. Решение 1. Определяем полезную мощность, используемую на движение с заданной скоростью: 2. По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды: Fдв = Fcопр. 3. Скорость движения судна v = 36 * 1000/3600 = 10 м/с 4. Сила сопротивления воды Сила сопротивления воды движению судна Fcопр. = 48 кН Решение 1. Резание осуществляется за счет трения между точильным камнем и обрабатываемой деталью: Решение Как известно, где Ап.с. — полезная работа; Адв — работа движущих сил. В рассматриваемом примере полезная работа — работа силы тяжести Вычислим работу движущих сил, т. е. работу вращающего момента на выходном валу лебедки: Угол поворота барабана лебедки определяется по уравнению равномерного вращения: где Тогда Подставив в выражение работы движущих сил числовые значения вращающего момента М и угла поворота φ, получим: Коэффициент полезного действия наклонной плоскости составит Контрольные вопросы и задания 1. Запишите формулы для расчета работы при поступательном и вращательном движениях. 2. Вагон массой 1000 кг перемещают по горизонтальному пути на 5 м, коэффициент трения 0,15. Определите работу силы тяжести. 3. Колодочным тормозом останавливают барабан после отключения двигателя (рис. 16.6). Определите работу торможения за 3 оборота, если сила прижатия колодок к барабану 1 кН, коэффициент трения 0,3. 4. Натяжение ветвей ременной передачи S1 = 700 Н, S2 = 300 Н (рис. 16.7). Определите вращающий момент передачи. 5. Запишите формулы для расчета мощности при поступательном и вращательном движениях. 6. Определите мощность, необходимую для подъема груза весом 0,5 кН на высоту 10 м за 1 мин. 7. Определите общий КПД механизма, если при мощности двигателя 12,5 кВт и общей силе сопротивления движению 2 кН скорость движения 5 м/с. 8. Ответьте на вопросы тестового задания. Тема 1.14. Динамика. Работа и мощность ЛЕКЦИЯ 17 infopedia.su Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени. Среднее значение мощности — это работа, выполненная за единицу времени. Величина мощности прямо пропорциональна величине совершённой работы \(A\) и обратно пропорциональна времени \(t\), за которое работа была совершена. Мощность \(N\) определяют по формуле: N=At. Единицей измерения мощности в системе \(СИ\) является \(Ватт\) (русское обозначение — \(Вт\), международное — \(W\)). Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт. Пример: Мощность двигателя автомобиля равна примерно \(90 л.с. = 66240 Вт\). Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля \(F\) и скорость его движения (v). N=F⋅v Эту формулу получают, преобразуя основную формулу определения мощности. Ни одно устройство не способно использовать \(100\) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству. Пример: Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах \(40 — 45\) %. Таким образом, получается, что только около \(40\) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля. Если мы заправим в бак автомобиля \(20\) литров бензина, тогда только \(8\) литров будут расходоваться на перемещение автомобиля, а \(12\) литров сгорят без совершения полезной работы. Коэффициент полезного действия обозначается буквой греческого алфавита \(«эта»\) η, он является отношением полезной мощности \(N\) к полной или общей мощности Nполная. Для его определения используют формулу: η=NNполная. Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет. Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η=NNполная⋅100%. Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы \(A\) к общей или полной проделанной работе Aполная. В этом случае формула для определения коэффициента полезного действия будет выглядеть так: η=AAполная⋅100%. Коэффициент полезного действия всегда меньше \(1\), или \(100\) % (η < 1, или η < \(100\) %). Источники: E. Šilters, V. Regusts, A. Cābelis. «Fizika 10. klasei», Lielvārds, 2004, 256 lpp. (Э. Шилтерс, В. Регустс, А. Цабелис. «Физика для 10 класса», Lielvārds, 2004, 256 стр.) www.yaklass.ru В процессе перемещения зарядов внутри замкнутой цепи, источником тока совершается определенная работа. Она может быть полезной и полной. В первом случае источник тока перемещает заряды во внешней цепи, совершая при этом работу, а во втором случае – заряды перемещаются во всей цепи. В этом процессе большое значение имеет КПД источника тока, определяемого, как соотношение внешнего и полного сопротивления цепи. При равенстве внутреннего сопротивления источника и внешнего сопротивления нагрузки, половина всей мощности будет потеряна в самом источнике, а другая половина выделится на нагрузке. В этом случае коэффициент полезного действия составит 0,5 или 50%. Рассматриваемый коэффициент полезного действия в первую очередь связан с физическими величинами, характеризующими скорость преобразования или передачи электроэнергии. Среди них на первом месте находится мощность, измеряемая в ваттах. Для ее определения существует несколько формул: P = U x I = U2/R = I2 x R. В электрических цепях может быть различное значение напряжения и величина заряда, соответственно и выполняемая работа тоже отличается в каждом случае. Очень часто возникает необходимость оценить, с какой скоростью передается или преобразуется электроэнергия. Эта скорость представляет собой электрическую мощность, соответствующую выполненной работе за определенную единицу времени. В виде формулы данный параметр будет выглядеть следующим образом: P=A/∆t. Следовательно, работа отображается как произведение мощности и времени: A=P∙∆t. В качестве единицы измерения работы используется джоуль (Дж). Для того чтобы определить, насколько эффективно какое-либо устройство, машина электрическая цепь или другая аналогичная система, в отношении мощности и работы используется КПД – коэффициент полезного действия. Данная величина определяется как отношение полезно израсходованной энергии, к общему количеству энергии, поступившей в систему. Обозначается КПД символом η, а математически определяется в виде формулы: η = A/Q x 100% = [Дж]/[Дж] х 100% = [%], в которой А – работа выполненная потребителем, Q – энергия, отданная источником. В соответствии с законом сохранения энергии, значение КПД всегда равно или ниже единицы. Это означает, что полезная работа не может превышать количество энергии, затраченной на ее совершение. Таким образом, определяются потери мощности в какой-либо системе или устройстве, а также степень их полезности. Например, в проводниках потери мощности образуются, когда электрический ток частично превращается в тепловую энергию. Количество этих потерь зависит от сопротивления проводника, они не являются составной частью полезной работы. Существует разница, выраженная формулой ∆Q=A-Q, наглядно отображающей потери мощности. Здесь очень хорошо просматривается зависимость между ростом потерь мощности и сопротивлением проводника. Наиболее ярким примером служит лампа накаливания, КПД у которой не превышает 15%. Остальные 85% мощности превращаются в тепловое, то есть в инфракрасное излучение. Рассмотренный коэффициент полезного действия всей электрической цепи, позволяет лучше понять физическую суть КПД источника тока, формула которого также состоит из различных величин. В процессе перемещения электрических зарядов по замкнутой электрической цепи, источником тока выполняется определенная работа, которая различается как полезная и полная. Во время совершения полезной работы, источника тока перемещает заряды во внешней цепи. При полной работе, заряды, под действием источника тока, перемещаются уже по всей цепи. В виде формул они отображаются следующим образом: На основании этого, можно вывести формулы полезной и полной мощности источника тока: В результате, формула КПД источника тока приобретает следующий вид: Максимальная полезная мощность достигается при определенном значении сопротивления внешней цепи, в зависимости от характеристик источника тока и нагрузки. Однако, следует обратить внимание на несовместимость максимальной полезной мощности и максимального коэффициента полезного действия. Коэффициент полезного действия источника тока зависит от многих факторов, которые следует рассматривать в определенной последовательности. Для определения величины тока в электрической цепи, в соответствии с законом Ома, существует следующее уравнение: i = E/(R + r), в котором Е является электродвижущей силой источника тока, а r – его внутренним сопротивлением. Это постоянные величины, которые не зависят от переменного сопротивления R. С их помощью можно определить полезную мощность, потребляемую электрической цепью: Таким образом, значение мощности с использованием конечных переменных будет отображаться в следующем виде: W1 = (E2 x R)/(R + r). Поскольку сила тока представляет собой промежуточную переменную, то в этом случае функция W1(R) может быть проанализирована на экстремум. С этой целью нужно определить значение R, при котором величина первой производной полезной мощности, связанная с переменным сопротивлением (R) будет равной нулю: dW1/dR = E2 x [(R + r)2 – 2 x R x (R + r)] = E2 x (Ri + r) x (R + r – 2 x R) = E2(r – R) = 0 (R + r)4 (R + r)4 (R + r)3 Из данной формулы можно сделать вывод, что значение производной может быть нулевым лишь при одном условии: сопротивление приемника электроэнергии (R) от источника тока должно достичь величины внутреннего сопротивления самого источника (R => r). В этих условиях значение коэффициента полезного действия η будет определяться как соотношение полезной и полной мощности источника тока – W1/W2. Поскольку в максимальной точке полезной мощности сопротивление потребителя энергии источника тока будет таким же, как и внутреннее сопротивление самого источника тока, в этом случае КПД составит 0,5 или 50%. electric-220.ru ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ: I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока. Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R® Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим: R0 = r. (4) Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока. При этом сила тока в цепи равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна Следовательно, полная мощность, выделяемая во всей цепи , определится формулой КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен Из формулы (8) следует, что т.е. Р1 изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании. Зависимость мощностей Р1, Рполн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1. Рис.1. I0 E/r Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р1, достигает наибольшего значения, к.п.д. в этот момент равен 50%. Рис. 2. Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку Подключите соединительные провода. Для этого нажмите кнопку провода 4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой Таблица 1. Исходные параметры электрической цепи Номер варианта 1 2 3 4 5 6 7 8 Е, В 10,0 9,5 9,0 8,5 8,0 8,5 9,0 9,5 r, Ом 4,8 5,7 6,6 7,5 6,4 7,3 8,2 9,1 5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2. 6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2. 7. Вычислите по формулам (2), (7), (8), (9) Р1, Р2, Рполн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2. 8. Постройте на одном листе миллиметровой бумаге графики зависимости P1 = f(R), P2 = f(R), Pполн=f(R), h = f (R) и U = f(R). 9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов. Таблица 2. Результаты измерений и расчётов R, Ом 2,0 2,5 3,0 … 20 U, В I, А P1, Вт P2, ВТ Pполн, ВТ h itteach.ru Каждая машина потребляет большую мощность, чем отдает, поскольку в ней происходят потери мощности (за счет трения, сопротивления воздуха, нагревания и т.д.) Коэффициент полезного действия представляет собой отношение отдаваемой мощности к подводимой мощности. Если:η — Коэффициент полезного действия, КПДPотд — Отданная мощность, т.е. полезная или эффективная мощность, равная подведенной мощности минус мощность потерь,Pподв — подведенная мощность, называемая также номинальной, приводной или индикаторной мощностью \[ η = \frac[-1.3]{P_{подв}-P_{потерь}}{P_{подв}} = 1 - \frac[-1.3]{P_{потерь}}{P_{подв}} = \frac[-1.3]{P_{отд}}{P_{подв}} \] Часто бывает целесообразно определить КПД не как отношение мощностей, а как отношение работ, особенно в тех случаях, когда работа над телом совершается не одновременно с работой, производимой самим телом, и с другой скоростью (например, растяжение и сжатие пружины). Поэтому КПД определяют также следующим образом: \[ КПД = \frac{Полезная работа}{Общая работа} \] \[ η = \frac[-1.3]{P_{отд}}{P_{подв}} · 100% \] \[ η= \frac[-1.3]{W_{отд}}{W_{подв}} · 100% \] При многократном превращении или передаче энергии общий коэффициент полезного действия равен произведению КПД на всех ступенях преобразования энергии: \[ η_{общ} = η_1 · η_2 · η_3 … η_m \] www.fxyz.ru Рассмотрим элементарную электрическую цепь, содержащую
источник ЭДС с внутренним сопротивлением r, и внешним сопротивлением R (рис. 7.5). КПД всегда определяем как отношение полезной работы к
затраченной: Полезная работа – мощность, выделяемая на внешнем сопротивлении Rв
единицу времени. По закону Ома имеем: а тогда . Таким образом, имеем, что при но при этом ток в цепи
мал и полезная мощность мала. Вот парадокс – мы всегда стремимся к повышенному
КПД, а в данном случае нам это не приносит пользы. Найдем условия, при которых полезная мощность будет
максимальна. Для этого нужно, чтобы . В выражении (7.8.2) , , следовательно, должно быть равно нулю выражение в
квадратных скобках, т.е. r=R. При этом
условии выделяемая мощность максимальна, а КПД равен 50%. Вышесказанное утверждение хорошо
иллюстрируется рисунком 7.7. Как видно из рисунка максимальный
КПД получается в данной цепи при уменьшении мощности. Рис. 7.7 ens.tpu.ru Полезная мощность (Useful capacity) – мощность ( машины, оборудования, энергетического агрегата или иного технического устройства) отдаваемая устройством в определенной форме и для определенной цели; равна полной мощности за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы. Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003. полезная мощность — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] полезная мощность Мощность (машины, оборудования, энергетического агрегата или иного технического устройства)… … Справочник технического переводчика полезная мощность — 3.10 полезная мощность: Эффективная мощность в киловаттах, полученная на испытательном стенде на хвостовике коленчатого вала или измеренная методом по ГОСТ Р 41.85. Источник … Словарь-справочник терминов нормативно-технической документации полезная мощность — naudingoji galia statusas T sritis Standartizacija ir metrologija apibrėžtis Galia, susijusi su tam tikros sistemos, įrenginio, aparato ar įtaiso atliekamu naudingu darbu. atitikmenys: angl. net power; useful power vok. Abgabeleistung, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas полезная мощность — naudingoji galia statusas T sritis fizika atitikmenys: angl. net power; useful power vok. Abgabeleistung, f; Nutzabgabe, f; Nutzleistung, f rus. полезная мощность, f pranc. puissance utile, f … Fizikos terminų žodynas Полезная мощность — мощность, которую можно получить на валу двигателя; то же, что Эффективная мощность … Большая советская энциклопедия Полезная мощность — – мощность, отдаваемая устройством в определенной форме и для определенной цели. СТ МЭК 50(151) 78 … Коммерческая электроэнергетика. Словарь-справочник Полезная мощность — English: Output power Мощность, отдаваемая устройством в определенной форме и для определенной цели (по СТ МЭК 50(151) 78) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь полезная мощность насоса — Мощность, сообщаемая насосом подаваемой жидкой среде и определяемая зависимостью где Q подача насоса, м3/с; P давление насоса, Па; QM массовая подача насоса, кг/с; LП полезная удельная работа насоса, Дж/кг; NП полезная мощность насоса, Вт. [ГОСТ… … Справочник технического переводчика полезная мощность (в автотранспортной технике) — полезная мощность Мощность, выраженная в киловаттах, полученная на испытательном стенде на хвостовике коленчатого вала или его эквивалента и измеряемая в соответствии с методом измерения мощности, установленным в ГОСТ Р 41.24. [ГОСТ Р 41.49 2003] … Справочник технического переводчика полезная мощность в ваттах — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN watts out … Справочник технического переводчика economic_mathematics.academic.ruТема 1.14. Работа и мощность. Коэффициент полезного действия. Полезная мощность формула
Тема 1.14. Работа и мощность. Коэффициент полезного действия.
 Мощность — работа, выполненная в единицу времени:
Мощность — работа, выполненная в единицу времени:



 Мощность при вращении (рис. 16.2)
Мощность при вращении (рис. 16.2)

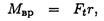
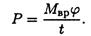
 получим
получим 


 Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.
Пример 1. Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.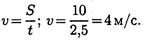

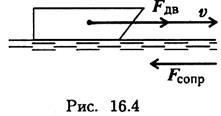


 Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.
Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.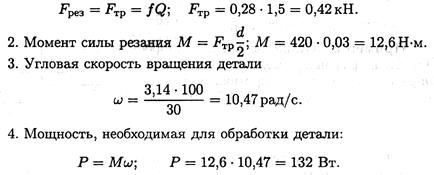
 Пример 4. Для того чтобы поднять волоком по наклонной плоскости на высоту H = 10 м станину массой т == 500 кг, воспользовались электрической лебедкой (рис. 1.64). Вращающий момент на выходном барабане лебедки М = 250 Н-м. Барабан равномерно вращается с частотой п = 30 об/мин. Для подъема станины лебедка работала в течение t = 2 мин. Определить коэффициент полезного действия наклонной плоскости.
Пример 4. Для того чтобы поднять волоком по наклонной плоскости на высоту H = 10 м станину массой т == 500 кг, воспользовались электрической лебедкой (рис. 1.64). Вращающий момент на выходном барабане лебедки М = 250 Н-м. Барабан равномерно вращается с частотой п = 30 об/мин. Для подъема станины лебедка работала в течение t = 2 мин. Определить коэффициент полезного действия наклонной плоскости.

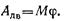



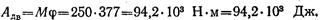



Мощность и коэффициент полезного действия — урок. Физика, 8 класс.
КПД источника тока: формулы
Содержание: КПД электрической цепи
Что такое КПД источника тока
Исследование мощности и КПД источника тока
Задачи на мощность тока и КПД
Исследование зависимости мощности и КПД источника тока от внешней нагрузки
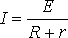 , (1)
, (1)МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ
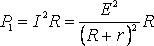 . (2)
. (2)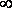 эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю:
эта мощность равна нулю. При всех других конечных значениях R мощность Р1> 0. Следовательно, функция Р1 имеет максимум. Значение R0, соответствующее максимальной мощности, можно получить, дифференцируя Р1 по R и приравнивая первую производную к нулю: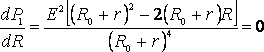 . (3)
. (3)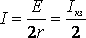 (5)
(5)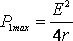 . (6)
. (6)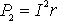 .
.  (7)
(7)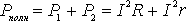 = I2(R+r) = IE (8)
= I2(R+r) = IE (8)КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
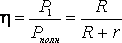 . (9)
. (9)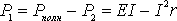 , (10)
, (10)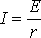 . Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид
. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид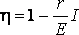 (11)
(11)

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

 э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.
э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с. в нижней части экрана) и амперметр (кнопка
в нижней части экрана) и амперметр (кнопка  там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр
там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр  , измеряющий напряжение на нагрузке.
, измеряющий напряжение на нагрузке. внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.
внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода. . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.
Вопросы и задания для самоконтроля
Коэффициент полезного действия КПД | Формулы и расчеты онлайн
Вычислить, найти коэффициент полезного действия, КПД, по формуле (5)
Общий коэффициент полезного действия, формула
Вычислить, найти общий коэффициент полезного действия, по формуле (6)
В помощь студенту
Коэффициент полезного действия КПД
стр. 471
КПД источника тока
(7.8.1)
.
(7.8.2) Полезная мощность - это... Что такое Полезная мощность?
Полезная мощность Смотреть что такое "Полезная мощность" в других словарях:
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: