Мощность в цепи постоянного тока определяется произведением напряжения на силу тока: P=U⋅I P=U⋅I . Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙Iхарактеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой: p=u⋅i p=u⋅i . Пусть напряжение на концах цепи меняется по гармоническому закону u=Um⋅cosωt u=Um⋅cosωt (с тем же успехом, разумеется, вместо u=Um⋅cosωt u=Um⋅cosωt можно было бы записать u=Um⋅sinωt u=Um⋅sinωt), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения: i=Im⋅cos(ωt+φc) i=Im⋅cos(ωt+φc) , где φc – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать: p=u⋅i=Um⋅Im⋅cosωt⋅cos(ωt+φc) p=u⋅i=Um⋅Im⋅cosωt⋅cos(ωt+φc) . При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период. Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов: cosα⋅cosβ=cos(α−β)+cos(α+β)2 cosα⋅cosβ=cos(α−β)+cos(α+β)2 . В рассматриваемом случае α = ω∙t и β = ω∙t + φc. Поэтому p=Um⋅Im2[cosφc+cos(2ωt+φc)]=Um⋅Im2cosφc+Um⋅Im2cos(2ωt+φc) p=Um⋅Im2[cosφc+cos(2ωt+φc)]=Um⋅Im2cosφc+Um⋅Im2cos(2ωt+φc) . Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени: P=Um⋅Im2cosφc P=Um⋅Im2cosφc . (10) При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно: P=Um⋅Im2=I2m⋅R2 P=Um⋅Im2=Im2⋅R2 . Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I2∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим P=I2m⋅R2=I2⋅R P=Im2⋅R2=I2⋅R или I2m2=I2 Im22=I2 . Действующим значением силы тока называют величину, в 2–√ 2 раз меньшую ее амплитудного значения: I=Im2√ I=Im2 . Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока. Аналогично можно доказать, что действующее значение переменного напряжения в 2–√ 2 раз меньше его амплитудного значения: U=Um2√ U=Um2 . Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать: P=Um2√⋅Im2√cosφc=U⋅Icosφc P=Um2⋅Im2cosφc=U⋅Icosφc . (10) Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле называется коэффициентом мощности. В случае, когда φc = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φc = - π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть. Рис. 10 Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит. При проектировании цепей переменного тока нужно добиваться, чтобы cos φc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов. Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85 Постоянный ток. Термин постоянный ток не совсем корректен: в действительности для постоянного тока неизменным является прежде всего значение напряжения (измеряется в Вольтах), а не значение тока (измеряется в Амперах), хотя значение тока также может быть неизменным. Путаница возникла в результате того, что термин ток употребляется для описания электрических процессов вообще. Поэтому термин постоянный ток следует понимать как постоянное напряжение. Далее будем использовать термин именно в этом смысле. Термин постоянный ток имеет несколько значений: · Питающее напряжение, величина которого не зависит от времени. Пример: устройство запитано от источника постоянного тока. В данном смысле использование термина постоянный ток (так же, как и переменный ток) подчёркивает «силовой» характер данного сигнала, то есть это электрический сигнал, передающий мощность, предназначенный для питания электрических устройств. В других смыслах используют более точные термины: напряжение, сигнал и т.п. · Постоянная составляющая сигнала. · Термин также может использоваться не в смысле напряжения, а в смысле частоты сигнала (для постоянного тока она нулевая). Пример: рабочий диапазон частот: от постоянного тока до 1 МГц Применение: Постоянный ток широко используется в технике: подавляющее большинство электронных схем в качестве питания используют постоянный ток. Переменный ток используется преимущественно для более удобной передачи от генератора до потребителя. Иногда в некоторых устройствах постоянный ток преобразуют в переменный ток преобразователями (инверторами). lektsia.com Мощность в цепи переменного тока. В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока. Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теориикомплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ(сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения. Единица измерения — ватт (W, Вт). Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ —угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью. Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии. studfiles.net Мгновенное значение мощности переменного тока равно произведению мгновенного значения напряжения на силу тока: , где и . Раскрыв , получим . Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что , , получим: где , поэтому среднее значение мощности будет равно: Такую же мощность развивает постоянный ток: . Величины и называются действующими (или эффективными) значениями тока и напряжения. Все амперметры и вольтметры градируются по действующим значениям тока и напряжения. Учитывая действующие значения тока и напряжения, выражение средней мощности (4.5.1) можно записать в виде: где множитель называется коэффициентом мощности. Формула (4.5.4) показывает, что мощность, выделяемая в цепи переменного тока, в общем случае, зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи отсутствует реактивное сопротивление Х, то и . Если цепь содержит только реактивное сопротивление (R = 0), то и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если имеет значение существенно меньше единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приводит либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить . Наименьшее допустимое значение для промышленных установок составляет примерно 0,85. В таблице 4.1 приведены сравнительные характеристики механических и электромагнитных колебаний. Таблица 4.1 Колебания механические электромагнитные Дифференциальное уравнение Дифференциальное уравнение Масса Индуктивность катушки Коэффициент жесткости Обратная величина емкости Смещение Заряд Скорость Сила тока Потенциальная энергия Энергия электрич. поля Кинетическая энергия Энергия магнитного поля Собств. частота пружинного маятника Собств. частота колебательного контура Период колебаний Период колеб. Формула Томсона Циклич. частота затухающих колебаний Циклич. частота затухающих колебаний Коэффициент затухания Коэффициент затухания Логарифмич. декремент затухания Логарифмич. декремент затухания Добротность пружинного маятника Добротность колебательного контура Резонансная частота Резонансная частота ens.tpu.ru Работа тока- это работа электрического поля по переносу электрических зарядов вдоль проводника;Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого работа совершалась. Применяя формулу закона Ома для участка цепи, можно записать несколько вариантов формулы для расчета работы тока: По закону сохранения энергии: работа равна изменению энергии участка цепи, поэтому выделяемая проводником энергияравна работе тока. В системе СИ: ЗАКОН ДЖОУЛЯ -ЛЕНЦА При прохождениии тока по проводнику проводник нагревается, и происходит теплообмен с окружающей средой, т.е. проводник отдает теплоту окружающим его телам. Количество теплоты, выделяемое проводником с током в окружающую среду, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику. По закону сохранения энергии количество теплоты, выделяемое проводником численно равно работе, которую совершает протекающий по проводнику ток за это же время. В системе СИ: [Q] = 1 Дж МОЩНОСТЬ ПОСТОЯННОГО ТОКА - отношение работы тока за время t к этому интервалу времени. В системе СИ: Первый закон Кирхгофа. Сколько тока втекает в узел, столько из него и вытекает. i2 + i3 = i1 + i4 Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным: 7. Расчет цепи методом эквивалентных структурных преобразований. Метод эквивалентных структурных преобразований. В основе различных методов преобразования электрических схем лежит понятие эквивалентности, согласно которому напряжения и токи в ветвях схемы, не затронутых преобразованием, остаются неизменными. Преобразования электрических схем применяются для упрощения расчетов. Рассмотрим наиболее типичные методы преобразования. Последовательное соединение элементов. При последовательном соединении элементов через них протекает один и тот же ток I (рис. 1.18). Согласно второму закону Кирхгофа, напряжение, приложенное ко всей цепи Для последовательного соединения сопротивлений r1,r2...rn (рис. 1.18) с учетом (1.6) будем иметь Ток в цепи с последовательным соединением элементов равен: а напряжение на n-ом элементе равно При последовательном соединении источников напряжения они заменяются одним эквивалентным источником с напряжением Uэкв, равным алгебраической сумме напряжений отдельных источников. Причем со знаком «+» берутся напряжения, совпадающие с напряжением эквивалентного источника, а со знаком «-» - несовпадающие (рис. 1.19). Параллельное соединение элементов. Соединение групп элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным (рис. 1.20). Согласно первому Кирхгофа, ток всей цепи I равен алгебраической сумме токов в параллельных ветвях, т.е. На основании этого уравнения с учетом (1.8) для параллельного соединения резистивных элементов получаем: где Токи и мощности параллельно соединенных ветвей при U=const (рис. 1.20) не зависят друг от друга и определяются по формулам: Мощность всей цепи равна : где rэ=1/gэ -эквивалентное сопротивление цепи. При увеличении числа параллельных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление соответственно уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность Р. Токи и мощности ранее включенных ветвей не изменяются. Рассмотрим частные случаи параллельного соединения резистивных элементов. а) параллельное соединение двух элементов б) параллельное соединение n ветвей с одинаковыми сопротивлениями infopedia.su Мощность в цепи постоянного и переменного тока. В цепи постоянного тока мощность потребляемая нагрузкой определяется по формуле: Опр. Среднюю за период мощность, потребляемую нагрузкой, для этого в начале найдём мгновенную мощность электрического тока в нагрузке. Нагрузка, потребляющая эл. энергию (мощность). Из ф. 2 видно, что мгновенная мощность содержит постоянную составляющую и переменную гармоническую составляющую удвоенной частоты. Найдём ср.мощность по ф. 1. Здесь U и I действующие значения тока и напряжения, а Внутри конденсатора протекает ток смещения сила которого численно равна: vunivere.ru Если напряжение в цепи переменного тока \(~U = U_0\sin wt,\) то мгновенное значение мощности переменного тока равно произведению мгновенных значений силы тока и напряжения \(~P = IU = I_0\sin \left( wt - \varphi\right)U_0\sin wt.\) Выполнив преобразование тригонометрической функции \(~\sin \left( wt - \varphi\right),\) получим Практический интерес представляет среднее по времени значение мощности. Если учесть, что \(~\mathcal h \sin^2 wt \mathcal i = \frac {1}2\) и \(~\mathcal h \sin wt \cos wt \mathcal i = 0,\) то среднее значение мощности за период будет равно где Id и Ud — действующие значения силы тока и напряжения. Множитель \(~\cos \varphi\) называют коэффициентом мощности. Последняя формула показывает, что мощность, выделяемая на участке цепи, состоящем из последовательно соединенных резистора, катушки и конденсатора переменного тока, зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Из рисунка 1 видно, что \(~\cos \varphi = \frac {U_{0R}}{U_0} = \frac {I_0 R}{I_0 Z} = \frac RZ.\) Рис. 1 Подставим в формулу средней мощности значение коэффициента мощности \(~\mathcal h P \mathcal i = \frac {I_d U_d R}{Z}.\) Но по закону Ома \(~I_d = \frac {U_d}{Z}.\) Следовательно, Таким образом, средняя мощность в цепи переменного тока равна средней мощности, выделяемой на активном сопротивлении R (см. Переменный ток). Это активная мощность, т.е. средняя мощность необратимых превращений в цепи переменного тока. Уменьшение \(~\cos \varphi \) приводит не только к неполному использованию мощности генератора электростанций (часть энергии возвращается в сеть — это реактивная мощность), но и к увеличению тепловых потерь в цепи (так как \(~ I = \frac {\mathcal h P \mathcal i}{U \cos \varphi},\) то \(~\Delta P = I^2 R = \frac {\mathcal h P^2 \mathcal i R}{U^2 \cos^2 \varphi}\)). Повышение коэффициента мощности электрических установок является важной народнохозяйственной задачей. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 408-409. www.physbook.ruРабота и мощность в цепи постоянного тока. Мощность в цепи
Мощность в цепи переменного тока

Мощность в цепи переменного тока
Активная мощность
Мощность, выделяемая в цепи переменного тока
, (4.5.1)
. (4.5.2)
, (4.5.4)
Работа и мощность в цепи постоянного тока.






 Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда. (1.27)
(1.27) (1.28)
(1.28)
 (1.29)
(1.29) (1.30)
(1.30) (1.31)
(1.31)
 (1.32)
(1.32) -эквивалентная проводимость.
-эквивалентная проводимость.
 (1.33)
(1.33) ,
,  (1.34)
(1.34)



 (1.36)
(1.36)Мощность в цепи постоянного и переменного тока
 (1). В цепи переменного тока мощность потребляемая нагрузкой имеет несколько значений.
(1). В цепи переменного тока мощность потребляемая нагрузкой имеет несколько значений.

 , где j – минимальная единица. Комплексное сопротивление
, где j – минимальная единица. Комплексное сопротивление  , его модуль называется полным сопротивлением нагрузки
, его модуль называется полным сопротивлением нагрузки  . В общем случае на комплексной нагрузке ток и напряжение имеют фазовый сдвиг
. В общем случае на комплексной нагрузке ток и напряжение имеют фазовый сдвиг  , где
, где  и
и 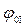 начальные фаза тока и напряжение на нагрузке. Математически уравнение мгновенных напряжения и тока:
начальные фаза тока и напряжение на нагрузке. Математически уравнение мгновенных напряжения и тока:  ;
;  , тогда мгновенное значение мощности найдется:
, тогда мгновенное значение мощности найдется: (2)
(2)
 (3)
(3) - коэффициент мощности нагрузки, определяющий способность нагрузки поглощать эл. энергию и превращать её в тепловую. Ф. 3 определяет активную мощность поглощаемой нагрузки. Реактивная мощность, проходящая через нагрузку определяется по формуле
- коэффициент мощности нагрузки, определяющий способность нагрузки поглощать эл. энергию и превращать её в тепловую. Ф. 3 определяет активную мощность поглощаемой нагрузки. Реактивная мощность, проходящая через нагрузку определяется по формуле  (4).
(4). Реактивная мощность нагрузкой не поглощается и возвращается в источник.
Реактивная мощность нагрузкой не поглощается и возвращается в источник. 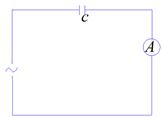
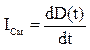 , где
, где  . Кроме реактивной мощности вводится понятие полной мощности нагрузки
. Кроме реактивной мощности вводится понятие полной мощности нагрузки  (5), где U и I действительное значение тока и напряжения
(5), где U и I действительное значение тока и напряжения 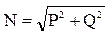 (6). Комплексная мощность нагрузки
(6). Комплексная мощность нагрузки  (7).
(7). Т. Мощность в цепи пер. тока — PhysBook
Мощность в цепи переменного тока

Литература
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: