Рассмотрим материальную точку М, к которой приложена сила F. Пусть точка переместилась из положения М0 в положение М1, пройдя путь s (рис. 1). Чтобы установить количественную меру воздействия силы F на пути s, разложим эту силу на составляющие N и R, направленные соответственно перпендикулярно направлению перемещения и вдоль него. Так как составляющая N (перпендикулярная перемещению) не может двигать точку или сопротивляться ее перемещению в направлении s, то действие силы F на пути s можно определить произведением Rs.
Эта величина называется работой и обозначается W.
Следовательно, W = Rs = Fs cos α, т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки. Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении.
Работа является скалярной величиной. Рассматривая работу силы, можно выделить три частных случая: сила направлена вдоль перемещения (α = 0˚), сила направлена в противоположном перемещению направлении (α = 180˚), и сила перпендикулярна перемещению (α = 90˚).
Исходя из величины косинуса угла α, можно сделать вывод, что в первом случае работа будет положительной, во втором – отрицательной, а в третьем случае (cos 90˚ = 0) работа силы равна нулю.
Так, например, при движении тела вниз работа силы тяжести будет положительной (вектор силы совпадает с перемещением), при подъеме тела вверх работа силы тяжести будет отрицательной, а при горизонтальном перемещении тела относительно поверхности Земли работа силы тяжести будет равна нулю. Силы, совершающие положительную работу, называются движущимися силами, силы, а совершающие отрицательную работу – силами сопротивления. Единицей работы принят джоуль (Дж):
1 Дж = сила×длина = ньютон×метр = 1 Нм. Джоуль – это работа силы в один ньютон на пути в один метр. *** На бесконечно малом участке ds криволинейный путь можно условно считать прямолинейным, а силу – постоянной.
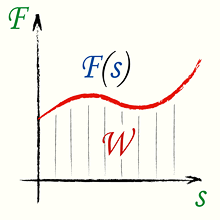
Тогда элементарная работа dW силы на пути ds равна dW = F ds cos (F,v). Работа на конечном перемещении равна сумме элементарных работ: W = ∫ F cos (F,v) ds. На рисунке 2а изображен график зависимости между пройденным расстоянием и F cos (F,v). Площадь заштрихованной полоски, которую при бесконечно малом перемещении ds можно принять за прямоугольник, равна элементарной работе на пути ds: dW = F cos (F,v) ds, а работа силы F на конечном пути s графически выражается площадью фигуры ОАВС, ограниченной осью абсцисс, двумя ординатами и кривой АВ, которая называется кривой сил. Если работа совпадает с направлением перемещения и возрастает от нуля пропорционально пути, то работа графически выражается площадью треугольника ОАВ (рис. 2 б), которая, как известно, может быть определена половиной произведения основания на высоту, т. е. половиной произведения силы на путь: W = Fs/2. *** Теорема: работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том же участке пути. Пусть к материальной точке М приложена система сил (F1, F2, F3,...Fn), равнодействующая которых равна FΣ (рис. 3). Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно, FΣ = F1 + F2 + F3 + .... + Fn. Спроецируем это векторное равенство на касательную к траектории, по которой движется материальная точка, тогда: FΣ cos γ = F1 cos α1 + F2 cos α2 + F3 cos α3 + .... + Fn cos αn. Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем полученное равенство в пределах какого-то конечного перемещения s: ∫ FΣ cos γ ds = ∫ F1 cos α1 ds + ∫ F2 cos α2 ds + ∫ F3 cos α3 ds + .... + ∫ Fn cos αn ds, что соответствует равенству: WΣ = W1 + W2 + W3 + ... + Wn или сокращенно: WΣ = ΣWFi Теорема доказана. *** Теорема: работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения. Пусть материальная точка М движется под действием силы тяжести G и за какой-то промежуток времени перемещается из положения М1 в положение М2, пройдя путь s (рис. 4).
На траектории точки М выделим бесконечно малый участок ds, который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна.
Из заштрихованного треугольника получим, что dy = ds cos α. Элементарная работа силы G на пути ds равна: dW = F ds cos α. Полная работа силы тяжести G на пути s равна W = ∫ Gds cos α = ∫ Gdy = G ∫ dy = Gh. Итак, работа силы тяжести равна произведению силы на вертикальное перемещение точки ее приложения: W = Gh; Теорема доказана. *** Задача: Однородный прямоугольный массив АВСD массой m = 4080 кг имеет размеры, указанные на рис. 5.
Определить работу, которую необходимо выполнить для опрокидывания массива вокруг ребра D. Решение.
Очевидно, что искомая работа будет равна работе сопротивления, совершаемой силой тяжести массива, при этом вертикальное перемещение центра тяжести массива при опрокидывании через ребро D является путем, который определяет величину работы силы тяжести. Для начала определим силу тяжести массива: G = mg = 4080×9,81 = 40 000 Н = 40 кН. Для определения вертикального перемещения h центра тяжести прямоугольного однородного массива (он находится в точке пересечения диагоналей прямоугольника), используем теорему Пифагора, исходя из которой: КО1 = ОD – КD = √(ОК2 + КD2) – КD = √(32 +42) - 4 = 1 м. На основании теоремы о работе силы тяжести определим искомую работу, необходимую для опрокидывания массива: W = G×КО1 = 40 000×1 = 40 000 Дж = 40 кДж. Задача решена. *** Представим себе диск, вращающийся вокруг неподвижной оси под действием постоянной силы F (рис. 6), точка приложения которой перемещается вместе с диском. Разложим силу F на три взаимно-перпендикулярные составляющие: F1 – окружная сила, F2 – осевая сила, F3 – радиальная сила. При повороте диска на бесконечно малый угол dφ сила F совершит элементарную работу, которая на основании теоремы о работе равнодействующей будет равна сумме работ составляющих. Очевидно, что работа составляющих F2 и F3 будет равна нулю, так как векторы этих сил перпендикулярны бесконечно малому перемещению ds точки приложения М, поэтому элементарная работа силы F равна работе ее составляющей F1: dW = F1ds = F1Rdφ. При повороте диска на конечный угол φ работа силы F равна W = ∫ F1Rdφ = F1R ∫ dφ = F1Rφ, где угол φ выражается в радианах. Так как моменты составляющих F2 и F3 относительно оси z равны нулю, то на основании теоремы Вариньона момент силы F относительно оси z равен: Мz(F) = F1R. Момент силы, приложенной к диску, относительно оси вращения называется вращающим моментом, и, согласно стандарту ИСО, обозначается буквой Т: Т = Мz(F), следовательно, W = Tφ. Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловое перемещение. *** Задача: рабочий вращает рукоятку лебедки силой F = 200 Н, перпендикулярной радиусу вращения.
Найти работу, затраченную в течение времени t = 25 секунд, если длина рукоятки r = 0,4 м, а ее угловая скорость ω = π/3 рад/с. Решение.
Прежде всего определим угловое перемещение φ рукоятки лебедки за 25 секунд: φ = ωt = (π/3)×25 = 26,18 рад. Далее воспользуемся формулой для определения работы силы при вращательном движении: W = Tφ = Frφ = 200×0,4×26,18 ≈ 2100 Дж ≈ 2,1 кДж. *** Работа, совершаемая какой-либо силой, может быть за различные промежутки времени, т. е. с разной скоростью. Чтобы охарактеризовать, насколько быстро совершается работа, в механике существует понятие мощности, которую обычно обозначают буквой P. Мощностью называется работа, совершаемая в единицу времени. Если работа совершается равномерно, то мощность определяют по формуле P = W/t. Если направление силы и направление перемещения совпадают, что эту формулу можно записать в иной форме: P = W/t = Fs/t или P = Fv. Мощность силы равна произведению модуля силы на скорость точки ее приложения. Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле: P = W/t = Tφ/t или P = Tω. Мощность силы, приложенной к равномерно вращающемуся телу, равна произведению вращающего момента на угловую скорость. Единицей измерения мощности является ватт (Вт): Ватт = работа/время = джоуль в секунду. *** Способность тела при переходе из одного состояния в другое совершать работу называется энергией. Энергия есть общая мера различных форм движения материи. В механике для передачи и преобразования энергии применяются различные механизмы и машины, назначение которых – выполнение заданных человеком полезных функций. При этом энергия, передаваемая механизмами, называется механической энергией, которая принципиально отличается от тепловой, электрической, электромагнитной, ядерной и других известных видов энергии. Виды механической энергии тела мы рассмотрим на следующей странице, а здесь лишь определимся с основными понятиями и определениями. При передаче или преобразовании энергии, а также при совершении работы, имеют место потери энергии, поскольку механизмы и машины, служащие для передачи или преобразования энергии преодолевают различные силы сопротивления (трения, сопротивления окружающей среды и т. п.). По этой причине часть энергии при передаче безвозвратно теряется и не может быть использована для выполнения полезной работы. Часть энергии, потерянная при ее передаче на преодоление сил сопротивления, учитывается при помощи коэффициента полезного действия механизма (машины), передающего эту энергию.
Коэффициент полезного действия (КПД) обозначается буквой η и определяется, как отношение полезной работы (или мощности) к затраченной: η = W2/W1 = P2/P1. Если коэффициент полезного действия учитывает только механические потери, то его называют механическим КПД. Очевидно, что КПД – всегда правильная дробь (иногда его выражают в процентах) и его значение не может быть больше единицы. Чем ближе значение КПД к единице (100 %), тем экономичнее работает машина. Если энергия или мощность передаются рядом последовательных механизмов, то суммарный КПД может быть определен, как произведение КПД всех механизмов: η = η1η2η3 ....ηn, где: η1, η2, η3, .... ηn– КПД каждого механизма в отдельности. *** Теоремы и законы динамики материальной точки k-a-t.ru нальности (∂f ∂ϕ)2 . Отсюда видно, что коэффициент инерции объекта зави- сит от выбора обобщенной координаты и может быть пересчитан. КЭ нестационарной голономной одностепенной системы имеет струк- туру квадратного полинома относительно обобщенной скорости q&, коэффи- циенты которой в общем случае зависят от q иt: 2T = aq&2 +2a1q& +2a0 , приa = a(q,t),a1 = a1 (q,t),a0 = a0 (q,t) (5.10) Размерность коэффициентов a,a0 ,a1 определяем по принципу Л.Эйлера: все слагаемые в выражениях должны иметь одинаковую размерность. Область пространства, в которой к материальному объекту приложена сила, называется векторным силовым полем. Эта область может быть трехмерной(например-шаровой),либо двумерной, либо представлять отрезок прямой или кривой линии. Обычно считают, что сила зависит только от координат (x,y,z) точки приложения силы, либо - от одной или двух координат, либо – постоянная по модулю и направлению. Допускаются также случаи, когда силы зависят и от скорости точки и от времени, т.е. сила задана в области пространства координат, скоростей, времени. Встречаются случаи, ко- гда сила зависит от ускорения. в мгновение t в системе отсчетаOxyz называется Мощностью силы F скаляр, равный скалярному произведению силы на скорость точки прило- F жения силы v в этой системе: м/c=Вт) (5.11) = = = + + = & + & + & P F v Fv cos(F,v ) Xvx Yvy Zvz Xx Yy Zz,(Н Согласно данному определению мощность силы есть положительный скаляр, если угол между силой и скоростью острый (в этом случае сила способствует движению, нарастанию кинетической энергии) и отрицательна, если угол тупой.(когда сила замедляет движение). Мощность силы равна нулю, если сила перпендикулярна к скорости точки приложения силы, или в случае, если точка приложения силы не имеет скорости. Мощности в двух системах отсчета различны в случае, если системы движутся одна относительно другой, поэтому следует указывать систему отсчета, в которой вычисляется мощность сил. Мощность сил трения, также как и других диссипативных сил, направленных против движения, отрицательна. Мощность силы сцепления колеса с дорогой (если нет проскальзывания колеса) равна нулю, поскольку точка приложения силы не имеет скорости. Рассмотрим случай, когда силы зависят только от положения точки при- ложения и мощность & P = Xx +Yy + Zz приводится к видуP =U , где & & & U (x,y,z) - функция положения точки приложения силы, т.е. – функция декартовых (или обобщенных) координат. В этом случае силуF(x,y,z) называютпотенциальной, а “силовую функцию”U с обратным знаком, называют 74 потенциальной энергией:П(x,y,z)= −U (x,y,z) . Область пространства, в ко- торой на тело действует потенциальная сила, называется потенциальным силовым полем. Под знаком производной можно добовлять любую константу, поэтому силовая функция и потенциальная энергия определяется с точностью до константы, определяющей уровень отсчета. В общем случае, потенциальную энергию можно определить как функциюП(q1,...,qn ) , получаемую путем преобразования мощности к виду: P = −П&(q1,...,qn ) , гдеqs – обобщен- ные координаты. Пусть тело произвольно движется в пространстве, т.е. оно перемещается вместе с полюсом O со скоростьюvO и вращается с угловой скоростьюω. Мощность пары сил, приложенной к твердому телу, не зависит от скорости полюса. Она равна скалярному произведению момента пары сил и угловой скорости. (5.12) P = M ω = Mω cos(M ,ω ) = M xωx+ M yωy+ M zωz, где M — момент пары сил,ω — угловая скорость твердого тела, которая, как известно, не зависит от выбора полюса. Мощность диссипативных пар сил отрицательна. Мощность пары сил не зависит от места приложения её к телу. Мощность пары сил трения в подшипнике отрицательная, поскольку момент трения и угловая скорость вращения противонаправлены. Мощность системы сил, приложенных к твердому телу, равна скалярному произведению главного вектора R системы на скорость любого полюса тела, сложенному со скалярным произведением главного моментаM 0 сил относительно этого полюса на угловую скорости тела: P = R vO+ M O ω при R = ∑Fi, MO= ∑ri×Fi. (5.13) Элементарной работой силы в выбранной системе координат Oxyz (неподвижной или подвижной) называется бесконечно малая величина, равная скалярному произведению силы на элементарное перемещение точки приложения силы в этой системе: (5.14) d ′A= F dr = Xdx +Ydy + Zdz = F |dr | cos(F,dr ), (Н м=Дж) Здесь через d΄A обозначена бесконечно малая работа, совершаемая силой за бесконечно малый интервал времени,dr - элементарное перемещение, сонаправленное со скоростью точки. Штрихом отмечено, чтоd΄A не всегда является полным дифференциалом от некоторой функции. Очевидно, что произведение Pdt равно элементарной работеd΄A: и наоборот, мощность равна отношению элементарной работы к элементар- ному времени: P=d΄A/dt. (5.16) 75 Мощность, умноженная на малый интервал времени ∆t, есть приближенное значение работы ∆A силы за этот интервал, мощность приближенно равна работе силы за 1 сек. Работой силы за конечный интервал времени [t1,t2] называется определенный интеграл от мощности по времени: t2 t2 (5.17) A12 = ∫Pdt= ∫ vdtпри v = r& = dr / dt. F t1 t1 Для расчета работы по данной общей формуле необходимо знать мощность как функцию времени или силу и скорость в виде функций только времени t. Но в некоторых частных случаях (случай потенциальной силы, случай постоянной силы трения при неизменном направлении движения) возможно вычисление работы без применения кинематических уравнений движения точки приложения силы, достаточно знать только начальное и конечное положение точки. Рассмотрим движение точки приложения силы по отношению к двум системам отсчета, движущимся одна относительно другой. Скорость точки в двух системах различна, поэтому и мощность силы будет различной. Таким образом, понятия мощность, работа, формулируется по отношению к конкретной системе отсчета, преимущественно – по отношению к ИСО или ПСО (инерционной или поступательной системам отсчета). Определение СилаF называетсяпотенциальной, а ее силовое поле - потенциальным силовым полем, если выполнены два условия: 1) Сила удовлетворяет одному из следующих условий: сила постоянна по величине и направлению F = const или зависит только от координат точки (всех трех или части) ее приложения, т.е.F = F(x,y,z). 2) Элементарная работа d′A силы есть полный дифференциал от некоторой функции координат, либо мощность силы в любой момент времени равна полной производной по времени от некоторой функцииΠ(x, y, z) (с выделенным знаком минус) : (5.18) ′ & d A = −dΠ(x,y,z) илиP = −Π(x,y,z). Функция П(x,y,z), получаемая посредством преобразования выражения элементарной работы, либо из выражения мощности, называетсяпо- тенциальной энергией потенциального силового поля в точке M(x, y, z). Тем самым векторному силовому полю силы F (x,y,z) сопоставляется математически более простое поле скалярной функции трех переменных П(x,y,z), либо - функции двух переменных П(x,y), либо - функции одной переменной П(x) Потенциальная энергия может быть представлена не только в декартовой системе координат, но также — в цилиндрической, сферической системах координат, в общем она является функцией некоторых обобщенных коорди- нат П(q1,q2,q3). 76 Поверхности, определенные уравнением П(q1,q2,q3)=C, где C - произвольно назначаемый постоянный параметр, называютсяэквипотенциальными поверхностями. Заметим, что под знаком дифференциала всегда можно прибавить или вычесть любую константу, так что функция П в формуле (5.18) определяется с точностью до константы. Константу произвольно назначают, например, полагают равной нулю, выбирая тем самым уровень отсчета семейства эквипотенциальных поверхностей. Мощность потенциальной силы равна взятой со знаком минус произ- водной по времени от потенциальной энергии P = −Π& . Подставим это выражение в определенный интеграл (5.17). Получим выражение работы потенциальной силы на конечном перемещении точки приложения силы, осуществленном за конечный промежуток времени: A12 = П(x1,y1,z1) – П(x2,y2,z2) = П1 – П2. (5.19) Таким образом, работа потенциальной силы при ее перемещении за ин- тервал [t1,t2] из точкиM1(x1,y1,z1) в точкуM2(x2,y2,z2) по любой траектории равна убыли потенциальной энергии на этом перемещении, т.е. равна разно- сти потенциальных энергий в первой и второй точках потенциального поля. Работа потенциальной силы не зависит от формы траектории, соединяющей две точки. В частности, работа потенциальной силы на любой замкнутой траектории равна нулю, а работа при переходе точки приложения силы с эквипотенциальной поверхности П=С1 на поверхность П=С2 равна разно- сти констант: А12=С1-С2. Частный случай В качестве начальной точкиM1(x1,y1,z1) возьмем любую точкуM(x,y,z) потенциального поля, а в качествеM2(x2,y2,z2) возьмем такую точку поляM(xO,yO,zO), в которой потенциальная энергия принята равной нулю. В этом случае формула (5.19) принимает вид П(x,y,z) =AMO =–AOM. (5.20) Получаем следующую физическую интерпретацию. Потенциальная энергия в любой точке M потенциального поля равна работе приложенной силы при перемещении ее точки приложения из положенияM по любой гладкой или негладкой траектории в такое положение, в котором потенциальная энергия принята равной нулю, а также равна взятой со знаком минус работе силы на перемещении в положениеM(x,y,z) из “нулевого” положения, в котором потенциальная энергия принята равной нулю. Пример 1 Найдем потенциальную энергию силы тяжестиG = −Gk , про- тивонаправленной с ортом k вертикальной осиOz системыOxyz. Методом элементарной работы получаем: d΄A =Gxdx +Gydy +Gzdz =–Gdz = –d(Gz) => П =Gz. Методом мощности получаем P =Gx x& +Gy y& +Gz z& = −Gz& = −(Gz) Π =Gz. Таким образом, потенциальная энергия силы тяжести равна произведению веса материальной точки на высоту расположения точки M над плоскостьюOxy, удовлетворяющей условиюz = 0. Здесь плоскостьOxy назначена 77 нулевой эквопотенциальной плоскостью. Потенциальная энергия силы тяжести отрицательна в точках, расположенных под плоскостью Oxy, приz < 0. На любых горизонтальных плоскостях данная потенциальная энергия одинакова во всех точках, т.е. горизонтальные плоскости являются эквипотенциальными поверхностями. Работа силы тяжести на перемещении с плоскости уровняz =z1 на плоскостьz =z2 определяется по формуле: A12 = П1 – П2 =G(z1 –z2) = ±Gh приh =|z1–z2|. Эта работа пропорциональна разности (убыли) уровней, она отрицательна, если первый уровень ниже, чем второй. Замечание. В случае если осьOz направлена вниз, получаем формулу с обратным знаком: П =–Gz. Пример 2. Потенциальная энергии силы упругости пружины. Силовое поле горизонтальной пружины имеет вид горизонтальной осиOx. Начало оси совместим со свободным концом недеформированной пружины,x — деформация растяжения пружины приx > 0, или сжатия пружины приx < 0. Упругая сила пружиныF = −cxi , гдеi — орт осиx. Она всегда направлена противоположно деформации. Методом мощности находим потенциальную энергию силы упругости P = Fx x= −c x x= −(c x 2 & , отсюда Π = cx 2 / 2 / 2) & & Вообразим, что пружина очень медленно растягивается внешней силой, медленно нарастающей от нуля до значения F вн = cxi . Считаем, что в каждый момент времени упругая сила пружины уравновешивает внешнию силу. Среднее значение величины силы F вн на интервале [0,x] равно:Fcр = cx / 2 . Упругая сила пружины, совершая при этом отрицательную работу по сопротивлению растягиванию, запасает в пружине положительную потенциальную энергию, равную Π = F x = cx2 / 2. ср Работа упругой силы на деформации = x2 − x1 равнаA12 = (x22 –x12)c/2. Очевидно, что A12 < 0 при x1 < x2 иA12 > 0 при x1 > x2 Пример 3. Сила тяготения Земли по закону "обратных квадратов": F =γm m/ r2 , = −γm mr /r3 , гдеr —радиус-векторматериальной точки в F 1 1 геоцентрической системе отсчета, γ = 6,672·10–11 (м3/(кг·с2) — постоянная тя- готения, r / r = e — ортрадиус-векторатела (материальной точки), проведенного из центра Земли,m1 = 6·1024 (кг)— масса Земли,m — масса тела, γm1 = 3986·1011 (м3/с2) - геоцентрическая гравитационная постоянная. Учитывая тождества r r = r2 , r dr = rdr находим , ′ γm1m γm1m γm1m γm1m d A = − r3 r dr = − r2 dr = d(− r ) Π(r) = − r . Отметим, что П(r)→0 приr→∞, следовательно, потенциальная энергия на бесконечности принята равной нулю. Пример 4. Работа постоянной по величине и направлению силы на F прямолинейном векторе перемещения s , образующим с силой угол α. Име- ем работу на перемещении [0, s]: 78 studfiles.net Слово «сила» настолько всеобъемлюще, что дать ему четкое понятие – задача практически невыполнимая. Разнообразие от силы мышц до силы разума не охватывает весь спектр вложенных в него понятий. Сила, рассмотренная как физическая величина, имеет четко определенное значение и определение. Формула силы задает математическую модель: зависимость силы от основных параметров. История исследования сил включает определение зависимости от параметров и экспериментальное доказательство зависимости. Сила – мера взаимодействия тел. Взаимное действие тел друг на друга полностью описывает процессы, связанные с изменением скорости или деформацией тел. За силу в 1 ньютон принята сила, под действием которой тело массой 1 кг изменяет свою скорость на 1 м за 1 секунду. Сила как векторная величина определяется: Описывая взаимодействие, обязательно указывают эти параметры. Виды природных взаимодействий: гравитационные, электромагнитные, сильные, слабые. Гравитационные силы (сила всемирного тяготения с ее разновидностью – силой тяжести) существуют благодаря влиянию гравитационных полей, окружающих любое тело, имеющее массу. Исследование полей гравитации не закончено до сих пор. Найти источник поля пока не представляется возможным. Больший ряд сил возникает вследствие электромагнитного взаимодействия атомов, из которых состоит вещество. При взаимодействии тела с Землей оно оказывает давление на поверхность. Сила давления, формула которой имеет вид: P = mg, определяется массой тела (m). Ускорение свободного падения (g) имеет различные значения на разных широтах Земли. Сила вертикального давления равна по модулю и противоположна по направлению силе упругости, возникающей в опоре. Формула силы при этом меняется в зависимости от движения тела. Действие тела на опору вследствие взаимодействия с Землей чаще именуют весом тела. Интересно, что величина веса тела зависит от ускорения движения в вертикальном направлении. В том случае, когда направление ускорения противоположно ускорению свободного падения, наблюдается увеличение веса. Если ускорение тела совпадает с направлением свободного падения, то вес тела уменьшается. К примеру, находясь в поднимающемся лифте, в начале подъема человек чувствует увеличение веса некоторое время. Утверждать, что его масса меняется, не приходится. При этом разделяем понятия «вес тела» и его «масса». При изменении формы тела (его деформации) появляется сила, которая стремится вернуть телу его первоначальную форму. Этой силе дали название "сила упругости". Возникает она вследствие электрического взаимодействия частиц, из которых состоит тело. Рассмотрим простейшую деформацию: растяжение и сжатие. Растяжение сопровождается увеличением линейных размеров тел, сжатие – их уменьшением. Величину, характеризующую эти процессы, называют удлинением тела. Обозначим ее "x". Формула силы упругости напрямую связана с удлинением. Каждое тело, подвергающееся деформации, имеет собственные геометрические и физические параметры. Зависимость упругого сопротивления деформации от свойств тела и материала, из которого оно изготовлено, определяется коэффициентом упругости, назовем его жесткостью (k). Математическая модель упругого взаимодействия описывается законом Гука. Сила, возникающая при деформации тела, направлена против направления смещения отдельных частей тела, прямо пропорциональна его удлинению: Знак «-» говорит о противоположности направления деформации и силы. В скалярной форме отрицательный знак отсутствует. Сила упругости, формула которой имеет следующий вид Fy = kx, используется только при упругих деформациях. Влияние магнитного поля на постоянный ток описывается законом Ампера. При этом сила, с которой магнитное поле действует на проводник с током, помещенный в него, называется силой Ампера. Взаимодействие магнитного поля с движущимся электрическим зарядом вызывает силовое проявление. Сила Ампера, формула которой имеет вид F = IBlsinα, зависит от магнитной индукции поля (В), длины активной части проводника (l), силы тока (I) в проводнике и угла между направлением тока и магнитной индукцией. Благодаря последней зависимости можно утверждать, что вектор действия магнитного поля может измениться при повороте проводника или изменении направления тока. Правило левой руки позволяет установить направление действия. Если левую руку расположить таким образом, чтобы вектор магнитной индукции входил в ладонь, четыре пальца были направлены по току в проводнике, то отогнутый на 90° большой палец покажет направление действия магнитного поля. Применение этому воздействию человечеством найдено, к примеру, в электродвигателях. Вращение ротора вызывается магнитным полем, созданным мощным электромагнитом. Формула силы позволяет судить о возможности изменения мощности двигателя. С увеличением силы тока или величины поля вращательный момент возрастает, что приводит к увеличению мощности двигателя. Взаимодействие магнитного поля с зарядом широко используется в масс-спектрографах при исследовании элементарных частиц. Действие поля при этом вызывает появление силы, названной силой Лоренца. При попадании в магнитное поле движущейся с некоторой скоростью заряженной частицы сила Лоренца, формула которой имеет вид F = vBqsinα, вызывает движение частицы по окружности. В этой математической модели v – модуль скорости частицы, электрический заряд которой – q, В – магнитная индукция поля, α – угол между направлениями скорости и магнитной индукции. Частица движется по окружности (либо дуге окружности), так как сила и скорость направлены под углом 90° друг к другу. Изменение направления линейной скорости вызывает появление ускорения. Правило левой руки, рассмотренное выше, имеет место и при изучении силы Лоренца: если левую руку расположить таким образом, чтобы вектор магнитной индукции входил в ладонь, четыре пальца, вытянутых в линию, были направлены по скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление действия силы. Взаимодействие магнитного поля и вещества используется в циклотронах. Проблемы, связанные с лабораторным изучением плазмы, не позволяют содержать ее в замкнутых сосудах. Высоко ионизированный газ может существовать только при высоких температурах. Удержать плазму в одном месте пространства можно посредством магнитных полей, закручивая газ в виде кольца. Управляемые термоядерные реакции можно изучать, также закручивая высокотемпературную плазму в шнур при помощи магнитных полей. Пример действия магнитного поля в естественных условиях на ионизированный газ – Полярное сияние. Это величественное зрелище наблюдается за полярным кругом на высоте 100 км над поверхностью земли. Загадочное красочное свечение газа пояснить смогли лишь в ХХ веке. Магнитное поле земли вблизи полюсов не может препятствовать проникновению солнечного ветра в атмосферу. Наиболее активное излучение, направленное вдоль линий магнитной индукции, вызывает ионизацию атмосферы. Исторически сложилось так, что основной величиной, характеризующей протекание тока в проводнике, называют силу тока. Интересно, что это понятие ничего общего с силой в физике не имеет. Сила тока, формула которой включает заряд, протекающий за единицу времени через поперечное сечение проводника, имеет вид: Фактически, сила тока – величина заряда. Единицей ее измерения является Ампер (А), в отличие от Н. Силовое воздействие на вещество сопровождается совершением работы. Работа силы – физическая величина, численно равная произведению силы на перемещение, пройденное под ее действием, и косинус угла между направлениями силы и перемещения. Искомая работа силы, формула которой имеет вид A = FScosα, включает величину силы. Действие тела сопровождается изменением скорости тела или деформацией, что говорит об одновременных изменениях энергии. Работа силы напрямую зависит от величины. fb.ru Работа - это скалярная величина, которая определяется по формуле Работу выполняет не тело, а сила! Под действием этой силы тело совершает перемещение. Обратите внимание, что у работы и энергии одинаковые единицы измерения. Это означает, что работа может переходить в энергию. Например, для того, чтобы тело поднять на некоторую высоту, тогда оно будет обладать потенциальной энергией, необходима сила, которая совершит эту работу. Работа силы по поднятию перейдет в потенциальную энергию. Правило определения работы по графику зависимости F(r): работа численно равна площади фигуры под графиком зависимости силы от перемещения. 1) Верно определяем направление силы, которая выполняет работу; 2) Изображаем вектор перемещения; 3) Переносим вектора в одну точку, получаем искомый угол. На рисунке на тело действуют сила тяжести (mg), реакция опоры (N), сила трения (Fтр) и сила натяжения веревки F, под воздействием которой тело совершает перемещение r. Работа силы тяжести Работа реакции опоры Работа силы трения Работа силы натяжения веревки Работу равнодействующей силы можно найти двумя способами: 1 способ - как сумму работ (с учетом знаков "+" или "-") всех действующих на тело сил, в нашем примере Для нахождения работы, совершенной силой упругости, необходимо учесть, что эта сила изменяется, так как зависит от удлинения пружины. Из закона Гука следует, что при увеличении абсолютного удлинения, сила увеличивается. Для расчета работы силы упругости при переходе пружины (тела) из недеформированного состояния в деформированное используют формулу Скалярная величина, которая характеризует быстроту выполнения работы (можно провести аналогию с ускорением, которое характеризует быстроту изменения скорости). Определяется по формуле КПД - это отношение полезной работы, совершенной машиной, ко всей затраченной работе (подведенной энергии) за то же время Коэффициент полезного действия выражается в процентах. Чем ближе это число к 100%, тем выше производительность машины. Не может быть КПД больше 100, так как невозможно выполнить больше работы, затратив меньше энергии. КПД наклонной плоскости - это отношение работы силы тяжести, к затраченной работе по перемещению вдоль наклонной плоскости. 1) Формулы и единицы измерения;2) Работу выполняет сила; 3) Уметь определять угол между векторами силы и перемещения Если работа силы при перемещении тела по замкнутому пути равна нулю, то такие силы называют консервативными или потенциальными. Работа силы трения при перемещении тела по замкнутому пути никогда не равна нулю. Сила трения в отличие от силы тяжести или силы упругости является неконсервативной или непотенциальной. Есть условия, при которых нельзя использовать формулу Значение работы некоторой силы зависит от выбора системы отсчета. fizmat.by Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу. Работа W есть произведение силы F на перемещение s. \[ W = F·s \] Работа — величина скалярная. Единица СИ работы \[ [W] = [F][s] = Ньютон·метр \] \[ [W] = Джоуль (дж) = Вт · с = кг · \frac[-1.2]{метр^2}{сек^2} \] Если сила F постоянна во времени и ее направление совпадает с направлением перемещения тела, то работа W находится по формуле. \[ W = F·s \] Здесь:W — совершенная работа (Джоуль),F — постоянная сила, совпадающая по направлению с перемещенем (Ньютон),s — перемещение тела (метр) Если сила и перемещение составляют между собой угол α 90º, то перемещение следует умножать на составляющую силы в направлении перемещения (или силу умножать на составляющую перемещения в направлении действия силы). В векторной форме \[ W = \vect{F}·\vect{s} \] \[ W = F·s·\cos(α) \] Здесь:α — угол между вектором силы и вектором перемещения, º Если сила не постоянна по величине и является функцией перемещения F = F(s), и направлена под углом α к перемещению, то работа есть интеграл от силы по перемещению. \[ W = \int\from{s_1}\to{s_2} \vect{F} d\vect{s} \] Площадь под кривой на графике зависимости F от s равна работе, произведенной данной силой www.fxyz.ruТехническая механика. Мощность силы формула
Работа и мощность силы - основные понятия и определения.
Работа, мощность, энергия
Работа постоянной силы на прямолинейном участке
Работа силы на криволинейном участке пути
Теорема о работе равнодействующей
Теорема о работе силы тяжести
Пример решения задачи по определению работы силы тяжести
Работа постоянной силы, приложенной к вращающемуся телу
Пример решения задачи
Мощность
Понятие об энергии и КПД
5.3. Мощность силы
5.4. Работа и потенциальная энергия
Формула силы. Сила - формула (физика)
Сила в физике
 Как физическая величина сила имеет единицу измерения (в системе СИ – Ньютон) и прибор для ее измерения – динамометр. Принцип действия силомера основан на сравнении силы, действующей на тело, с силой упругости пружины динамометра.
Как физическая величина сила имеет единицу измерения (в системе СИ – Ньютон) и прибор для ее измерения – динамометр. Принцип действия силомера основан на сравнении силы, действующей на тело, с силой упругости пружины динамометра.Сила давления
Изменение веса тела
Сила упругости

Взаимодействие магнитного поля с током

Траектории частиц

Проблемы плазмы

Явления, связанные с движением заряда
Определение работы силы
Работа равнодействующей силы, тяжести, трения, упругости. Мощность, коэффициент полезного действия. Примеры, формулы
Тестирование онлайн
Работа



Угол между вектором силы и перемещением









Работа равнодействующей силы
 2 способ - в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок
2 способ - в первую очередь найти равнодействующую силу, затем непосредственно ее работу, см. рисунок

Работа силы упругости


Мощность


Коэффициент полезного действия


Главное запомнить
 Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:
Если сила является переменной, если траектория движения является кривой линией. В этом случае путь разбивается на малые участки, для которых эти условия выполняются, и подсчитать элементарные работы на каждом из этих участков. Полная работа в этом случае равна алгебраической сумме элементарных работ:
Работа | Формулы и расчеты онлайн
Работа постоянной силы, формула
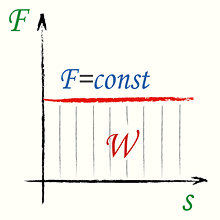
Вычислить, найти работу постоянной силы по формуле (4)
Работа постоянной силы, направленной под углом к перемещению, формула
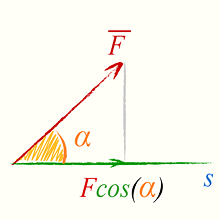
Вычислить, найти работу постоянной силы направленной под углом к перемещению по формуле (4)
Работа переменной силы, направленной под углом к перемещению, формула
В помощь студенту
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: