Потерями мощности называется мощность, потребляемая элементами сети при передаче энергии или просто при нахождении сети под напряжением. Они подразделяются на потери активной и реактивной мощности, на условно-постоянные и условно-переменные потери, а также на потери в линиях, трансформаторах и других элементах сети. Условно-переменными (нагрузочными) называются потери, которые возникают в продольных ветвях схем замещения элементов сети. Эти потери пропорциональны квадрату тока нагрузки, который сильно меняется во времени. Поэтому нагрузочные потери также подвержены большим изменениям. Условно-постоянными называются потери, возникающие в поперечных ветвях схем замещения. Эти потери приближенно можно считать пропорциональными квадрату напряжения. Они мало зависят от тока нагрузки и возникают даже при его отсутствии, то есть на холостом ходу. Поэтому их называют также потерями холостого хода. Поскольку напряжение в сети мало меняется во времени, то потери холостого хода остаются почти постоянными. Нагрузочные потери активной, реактивной и полной мощности в линии электропередачи пропорциональны квадрату передаваемой мощности , (19.1) , (19.2) . (19.3) где активное сопротивление линии, Ом; индуктивное сопротивление линии, Ом; передаваемая мощность, кВА; номинальное напряжение, кВ. К условно-постоянным потерям активной мощности в линиях относятся потери на коронный разряд, потери в изоляторах, а также диэлектрические потери в изоляции кабелей и воздушных линий с изолированными проводами. Условно-постоянные потери реактивной мощности в линиях – это потери в емкости. Поскольку емкость генерирует реактивную мощность, то они отрицательны и вместо них обычно используется обратная им по знаку величина зарядной мощности. Для линии в целом эта мощность равна , (19.4) где Uср.кв – среднеквадратичное напряжение в линии, которое при приближенных расчетах может быть принято равным номинальному напряжению, кВ. Суммарные потери полной мощности в линиях определяются по выражению , (19.5) где ΔРкор – потери мощности на коронный разряд, кВт. Нагрузочные потери мощности в двухобмоточных трансформаторах определяются аналогично потерям в линиях по выражениям , ,, (20.1) где активное сопротивление трансформатора, Ом; индуктивное сопротивление трансформатора, Ом; S – мощность, передаваемая через трансформаторную подстанцию, кВА; фактическое или номинальное напряжение на стороне высшего напряжения, кВ. Условно-постоянные потери мощности в трансформаторах – это потери холостого хода. Суммарные потери полной мощности в двухобмоточных трансформаторах равны , , (20.2) где активные потери холостого хода, кВт реактивные потери холостого хода, кВАр. Потери мощности можно также выразить через каталожные данные трансформаторов: . (20.3) где Sном – номинальная мощность трансформатора, МВА; Uв,ном – номинальное высшее напряжение трансформатора, кВ; Uк%. – напряжение короткого замыкания, %; ΔРкз – потери короткого замыкания, кВт; nт – число трансформаторов. studfiles.net Сечения проводов, выбранные по условию минимума расхода проводникового материала, не обеспечивают минимальных потерь мощности. Найдем сечения проводов, которые отвечают условию min. Для ЛЭП, приведенной на рис. 11.1, потери активной мощности рассчитываются по формуле: (11.2) Обозначим объем проводникового материала одной фазы на всей ЛЭП через V, на первом участке – V1. Тогда величины сечений участков будут равны: и . Подставим эти выражения в формулу (11.2) и получим: В этой формуле все величины известны, кроме V1. Для определения минимума потерь активной мощности необходимо взять частную производную по неизвестной величине и приравнять ее к нулю: Получим равенство: . Сократим полученное выражение на : . (11.3) Так как , а, то формулу (11.3) можно переписать следующим образом: . Выразим мощности участков через токи и номинальное напряжение ЛЭП: Отношение тока к сечение называется плотностью тока (А/мм2). Таким образом, получено условие, при выполнении которого при выборе сечений, потери активной мощности будут наименьшими: = const. Значение плотности тока определяется по допустимой доле потери напряжения в активных сопротивлениях: . Сечения на участках рассчитываются по токам участков: где Сечения проводов округляют до ближайших стандартных и проверяют по потере напряжения и нагреву. Если сечения не удовлетворяют допустимой потере напряжения, то увеличивают сечения на тех участках, величина потери напряжения на которых наибольшая. Выбор сечений по допустимой потере напряжения выполняется по следующему алгоритму: Задаются значением x0ср в указанных диапазонах его изменения. Вычисляют долю потери напряжения в реактивных сопротивлениях . Вычисляют допустимую потерю напряжения в именованных единицах: Вычисляют допустимую долю потерь напряжения в активных сопротивлениях . Рассчитывают сечение провода, исходя из заданного условия. 5.1 постоянство сечений на всех участках: F=…; 5.2 минимальный расход проводникового материала: kр = … → F=…; 5.3 минимальные потери активной мощности: = … →F=…. Сечения проводов округляют до ближайших стандартных и проверяют по потере напряжения (общая формула): Если сечения не удовлетворяют допустимой потере напряжения, то увеличивают сечения на тех участках, величина потери напряжения на которых наибольшая. Проверку повторяют. Окончательно выбранное сечение проверяют по нагреву: Определение сечения по допустимой потере напряжения применяют к линиям местных сетей, сечения которых не выбирают по экономической плотности тока. Выбор сечения по условиям минимального расхода проводникового материала (min) и минимальных потерь активной мощности (min) дают более экономичные результаты, чем при условии постоянства сечений на всех участках (F=const). Выбор сечения при условии min приводит к экономии капитальных вложений и постоянных эксплуатационных расходов (обслуживание и ремонт ЛЭП). Метод применяют для потребителей с малым числом использования максимальной нагрузки Тм и малых токовых нагрузках. Для потребителей с большими токовыми нагрузками и значительной величиной Тм лучше использовать метод выбора сечений из условия min. Это приводит к уменьшению переменных эксплуатационных расходов, связанных с потерями мощности (электроэнергии) в ЛЭП. Выбор сечения по экономической плотности тока учитывает оба фактора. Поэтому метод является основным. Если длина ЛЭП велика, то сечение, выбранное по экономической плотности тока jэк, может не обеспечить допустимую потерю напряжения. Это приводит к необходимости пересчета сечения. Поэтому нужно сначала определить плотность тока из условия допустимой потери напряжения . Эту плотность тока сравнивают с экономической. Сечение рассчитывают по плотности тока, величина которой меньше. Лекция № 12 Расчет режимов простых замкнутых сетей План. Расчет линий с двухстронним питанием. Частные случаи расчета простых замкнутых сетей. studfiles.net Для определения потерь мощности в линии электропередачи следует определить параметры схемы замещения. Рисунок 2 – «П»-образная схема замещения линии электропередачи Таблица 6 – Расчет параметров «П»-образной схемы замещения линии электропередачи Расчетный параметр Формула определения Активное сопротивление ЛЭП, , Ом , где– удельное активное сопротивление, Ом/км, принять из справочников;L– длина, км, принять из задания пункт 2.10; М – количество цепей линии, принять из задания пункт 2.9. Реактивное сопротивление ЛЭП, ,Ом , где– удельное реактивное сопротивление, Ом/км, принять из справочников. Реактивная емкостная проводимость ЛЭП, ,См , где– удельная емкостная проводимость, См/км, принять из справочников. Таблица 7 – Расчетные формулы потерь в элементах схемы замещения ЛЭП Расчетный параметр Формула определения Потери реактивной мощности в емкостной проводимости, кВАр Потери активной мощности, кВт Потери реактивной мощности, кВАр Мощность ИП с учетом потерь в ЛЭП, кВт Мощность ИП с учетом потерь в ЛЭП, кВАр РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. В режимах максимальных нагрузок и минимальных нагрузок напряжение на шинах источника питания определяется по выражению , кВ где - отклонение напряжения на шинах, смотри задание пункт 2.8. Падение напряжение до шин ВН трансформатора определяется как , кВ Уровень напряжения , кВ РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. Таблица 8 – Уровень напряжения на шинах потребителей приведенное к высокой стороне трансформатора Расчетный параметр Формула определения Падение напряжения до точки «1`», кВ Уровень напряжения в точке «1`», кВ Падение напряжения до точки «а», кВ Уровень напряжения в точке «а», кВ Падение напряжения до точки «2», кВ Уровень напряжения в точке «2»(шина СН), кВ Падение напряжения до точки «3», кВ Уровень напряжения в точке «3» (шина НН), кВ РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. Таблица 9 – Определение реального значения уровня напряжения на шинах потребителей Расчетный параметр Формула определения Номинальный коэффициент трансформации СН Номинальный коэффициент трансформации НН Реальный уровень напряжения на шине СН, кВ Реальный уровень напряжения на шине НН, кВ РАСЧЕТ ПРОИЗВЕСТИ НА ВСЕ РЕЖИМЫ. ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ ПРИВЕСТИ ТАБЛИЧНО. ПОКАЗАТЬ ЧИСЛЕННЫЙ РАСЧЕТ ОДНОГО ИЗ РЕЖИМОВ. studfiles.net Глава 5. Потери мощностии электроэнергии в электрических сетях 5.1. Потери мощности в линиях Потери активной мощности в линиях обусловлены активными сопротивлениями проводов и кабелей, а также потерями на корону в воздушных линиях и на токи утечки через изоляцию в кабельных линиях высоких напряжений. В трехфазной линии, где нагрузка задана в виде полного тока Если нагрузка задана в виде полной Как видно, величина потерь зависит от передаваемой мощности и уровня напряжения. Повышение уровня напряжения позволяет снизить потери активной мощности в сопротивлении линии. Однако следует заметить, что при повышении напряжения в сетях, непосредственно питающих электроприемники, в соответствии со статическими характеристиками нагрузки по напряжению (см.§ 4.5) может увеличиться мощность потребителей и значит передаваемая по линии мощность. Мощность, передаваемая по линии, включает активную и реактивную составляющие. Если единственным источником активной мощности являются генераторы электрических станций, то реактивная мощность вырабатывается различными устройствами. Причем некоторые из них (компенсирующие устройства) могут устанавливаться вблизи потребителей реактивной мощности. Рассмотрим линию (рис.5.1), по которой передается мощность Установим в конце линии, например, батарею конденсаторов мощностью Снижение потерь активной мощности составит Количественной характеристикой эффективности снижения потерь мощности от компенсации реактивной мощности служит экономический эквивалент реактивной мощности Он показывает, на сколько снижаются потери активной мощности при включении в узле нагрузки компенсирующего устройства величиной В воздушных линиях высокого напряжения имеют место потери активной мощности на корону, которые в линиях напряжением 330 кВ и выше определяют по выражению (4.10). Как отмечалось, величина удельных потерь на корону Зависимость усредненных потерь мощности на корону от напряжения имеет вид где U – напряжение, В. Таким образом, при повышении уровня напряжения потери активной мощности на корону увеличиваются, но одновременно уменьшаются потери активной мощности в сопротивлении линии. Для кабелей высокого напряжения потери активной мощности, вызванные токами утечки через изоляцию, можно рассчитать по их активной проводимости Наряду с потерями активной мощности в линиях электропередачи теряется и реактивная мощность. Эти потери обусловлены индуктивными сопротивлениями воздушных и кабельных линий . Если нагрузка линии задана током, то потери реактивной мощности можно найти по формуле Для нагрузки, заданной мощностью, потери реактивной мощности в линии равны Наряду с потреблением реактивной мощности линия, обладая емкостной проводимостью и соответствующей ей зарядной мощностью vunivere.ru Ранее рассматривались разомкнутые сети. Ниже будут рассматриваться замкнутые сети. Напомним, что в разомк- нутых сетях все узлы получают питание только по одной ветви, что видно из примеров неразветвленной разомкну- той сети (рис. 3.13, а) и разветвленной разомкнутой сети (рис. 3.13,б). В простых замкнутых сетях есть узлы, питающиеся по двум ветвям, но нет узлов, получающих питание более чем по двум ветвям, отсутствуют узлы, с которыми соединены три и более ветви (рис. 3.14, а, б). Простые замкнутые сети содержат только один контур. Х Рис. 3.13. Примеры простых разом- кнутых сетей: а — неразветвленной; б — разветвлен- нойРасчет сечений проводов из условия минимума потерь мощности в сети. Мощность потерь формула
18. Классификация потерь мощности в электрических сетях.
19. Потери мощности в линиях электропередачи.
20. Потери мощности в трансформаторах.
Расчет сечений проводов из условия минимума потерь мощности в сети
Этапы расчета при разных условиях
Сравнительная характеристика методов
Определение потерь мощности в лэп
Определение уровня напряжения на шинах понижающей подстанции
Выбор рабочих ответвлений понижающего трансформатора определение уровня напряжения на шинах сн и нн трансформатора
Потери мощности электроэнергии в электрических сетях
 или его активной
или его активной 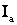 и реактивной
и реактивной  составляющих, потери активной мощности , расходуемые в активном сопротивлении
составляющих, потери активной мощности , расходуемые в активном сопротивлении  линии на нагрев проводников, определяют по формулам
линии на нагрев проводников, определяют по формулам . (5.1)
. (5.1) , активной
, активной  и реактивной
и реактивной  мощности, то те же потери можно найти по выражениям
мощности, то те же потери можно найти по выражениям . (5.2)
. (5.2) . Потери активной мощности в ней
. Потери активной мощности в ней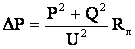 .
. . При этом передаваемая по линии реактивная мощность снизится до величины
. При этом передаваемая по линии реактивная мощность снизится до величины 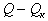 , а значит уменьшатся и потери активной мощности
, а значит уменьшатся и потери активной мощности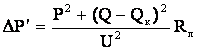 .
.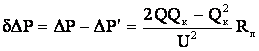 (5.3)
(5.3) (5.4)
(5.4)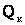 .
. во многом зависит от погодных условий и от напряжения.
во многом зависит от погодных условий и от напряжения. , (5.5)
, (5.5)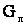
 . (5.6)
. (5.6)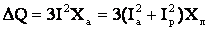 .
.  . (5.7)
. (5.7) , является источником реактивной мощности. Зарядная мощность линии, определяемая формулой (4.14), в некоторых случаях снижает реактивную мощность, передаваемую по линии, а значит и потери активной и реактивной мощности. Вместе с тем, в режимах наименьших нагрузок, когда имеет место избыток реактивной мощности, зарядная мощность может вызвать увеличение передаваемой по линии реактивной мощности и потерь мощности.
, является источником реактивной мощности. Зарядная мощность линии, определяемая формулой (4.14), в некоторых случаях снижает реактивную мощность, передаваемую по линии, а значит и потери активной и реактивной мощности. Вместе с тем, в режимах наименьших нагрузок, когда имеет место избыток реактивной мощности, зарядная мощность может вызвать увеличение передаваемой по линии реактивной мощности и потерь мощности.3.13. Распределение потоков мощности и напряжений в простых замкнутых сетях
а — треугольник; б — линия с двусторонним питанием; в — сложнозамкнутая сеть
является кольцевая сеть (рис. 3.14, а). Она содержит один замкнутый контур. В качестве источников питания могут служить или электростанции, или шины подстанций, в свою очередь связанные сетью с электростанциями системы. Кольцевая сеть на рис. 3.14, а может быть представлена в виде линии с двухсторонним питанием (рис. 3.14, б). Дей- ствительно, если источник питания в узле 1 мысленно раз- делить на два и представить в виде узлов 1 и 4, то из коль- цевой сети на рис. 3.14, а получим линию с двухсторонним питанием на рис. 3.14,б.
В сложной замкнутой сети есть узел, с которым соеди- нены три ветви или более (рис 3.14, в). Сложная замкну- тая сеть содержит два и более контуров.
К достоинствам замкнутых сетей следует отнести по- вышенную надежность электроснабжения потребителей, меньшие потери мощности, к недостаткам — сложность эксплуатации, удорожание за счет дополнительных линий. Расчеты замкнутых сетей сложнее, чем разомкнутых.
Распределение потоков мощности в простой замкнутой сети без учета потерь мощности. Представим простейшую замкнутую сеть в виде линии с двухсторонним питанием ( рис. 3.15, а) и рассмотрим различные случаи.
Рис. 3.15. Распределение потоков мощности в линии с двухсторонним питанием без учета потерь мощности:
а—схема замещения линии с четырьмя узлами; б—иллюстрация второго закона Кирхгофа; в—линия с п узлами; г, д—распределение Р и в однородной линии; е—линия с четырьмя узлами при ; ж, з—эквивалентное представление линии на рис, е; и—схема кольцевой сети 110 кВ
Заданы одинаковые напряжения по концам линии . Известны мощности нагрузки ,, сопротивления участков линии , где k. — узел начала участка линии; j — узел конца.
Принимаем следующие допущения:
а) пренебрегаем потерями мощности при опреде- лении потоков ;
б) предполагаем, что ток участка определяется по но- минальному напряжению:
;
в) используем расчетные мощности нагрузок под- станции.
При равенстве напряжений источников питания на ос- новании второго закона Кирхгофа можно записать (рис. 3.15,б)
.
Если заменим в последнем выражении все комплексные величины на сопряженные, то получим следующее урав- нение:
. (3.70)
Так как потери мощности не учитываются, первый за- кон Кирхгофа для узлов 2 и 3 можно записать так:
; (3.71)
. (3.72)
Подставив значения мощностей (3.71) и (3.72) в урав- нение (3.70), получим уравнение с одним неизвестным:
.
Отсюда находим значение потока мощности :
, (3.73)
где
.
Аналогично можно вывести формулу для определения потока мощности :
, (3.74)
где .
Значение потока мощности можно легко найти на основании первого закона Кирхгофа из (3.71).
Пример 3.9. Кольцевая сеть (рис. 3.15, и) напряжением 110 кВ свя- зывает электростанцию 1 с понижающими подстанциями 2, 3, имеющими расчетные нагрузки МВА и МВА. Марки проводов, длины линий указаны на рисунке. Со- противления их равны: Ом; Ом; Ом. Напряжение на шинах электростанции равно 117,7 кВ. Определим мощность, которая поступает с шин электростанции. Расчет проведем без учета потерь мощности.
Составим схему замещения сети в виде линии с двухсторонним пи- танием, разрезая кольцо в узле 1 (рис. 3.15,а). Определим по выраже- иям (3.73) и (3.74) приближенное потокораспределение в кольце с целью выявления точки потокораздела:
МВА;
МВА.
Проверим правильность определения потоков мощности на голов- ных линиях кольца по условию :
.
Значения и определены верно. Находим поток мощности в линии 23 по первому закону Кирхгофа для узла 2:
МВА.
Узел 3 — точка потокораздела активной и реактивной мощности. Мощность, поступающая с шин электростанции и определенная без уче- та потерь мощности, равна
МВА.
Рассмотрим линию с количеством узлов, равным п (рис. 3.15,в). Потоки мощности на головных участках оп- ределятся так:
, (3.75)
. (3.76)
Если известны токи нагрузок , то можно определить токи на головных участках линии аналогично (3.75), (3.76):
, (3.77)
. (3.78)
В однородной сети отношение активного и реактивного сопротивлений всех ветвей схемы замещения сети одина- ково:
, (3.79)
поэтому формулу (3.75) для однородной сети можно запи- сать в виде
или
. (3.75а)
Аналогично для однородной сети из (3.76) можно по- лучить следующее выражение:
. (3.76а)
В однородной сети, все участки которой выполнены про- водами (кабелями) одного сечения с удельными актив- ным и реактивным сопротивлениями , , распределение мощностей можно находить по длинам участков, посколь- ку сопротивление каждой ветви kj
.
При одинаковом сечении проводов вдоль всей линии формулы (3.76) и (3.77) принимают вид
(3.80)
где , , — длины участков линии между узлами со- ответственно k и п, 1 и k, 1 и n.
Выведенные формулы показывают, что в однородных сетях распределения активных и реактивных мощностей (токов) не зависят друг от друга. Нахождение распределе- ния Р и Q в таких сетях, упрощается. Рассчитываются как бы две независимые сети: одна — нагруженная только ак- тивными нагрузками (рис. 3.15, г) и вторая—реактивны- ми (рис. 3.15, д). Для каждой из них определяется распре- деление мощностей. По схеме на рис. 3.15, г определяется распределение активных мощностей, а по схеме на рис. 3.15, д—реактивных. Полные мощности на участках сети (рис. 3.15, в) находятся суммированием проходящих по ним активных и реактивных мощностей. Такой расчетный прием, называемый расщеплением сети (см. § 10.4), умень- шает трудоемкость расчета сети.
Следует обратить внимание на то, что равенство сече- ний проводов на всех участках сети не позволяет считать сеть однородной. Нужно, чтобы и удельные реактивные сопротивления линий на всех участках сети были также равными.
Сеть, один участок которой выполнен кабелем, а дру- гой — воздушной линией, даже при равных сечениях про- водов и жил кабелей и выполнении их из одного и того же металла не будет однородной. Неоднородной будет и воз- душная сеть, по всей длине которой подвешены одни и те же провода, но с неодинаковым среднегеометрическим рас- стоянием между ними на разных участках сети. В обоих случаях при равенстве удельных активных сопротивлений участков линии удельные реактивные сопротивления будут не равны.
Искусственными мерами сеть с неодинаковыми сечения- ми и расположением проводов на разных участках можно сделать однородной. Достигается это последовательным включением конденсатора на некоторых участках сети; со- противления конденсаторных батарей берутся такими, что- бы отношения активного и реактивного сопротивлений от- дельных участков сети стали одинаковыми. В результате можно в некоторых случаях снизить потери мощности и электроэнергии в сети и улучшить режим напряжения у потребителей (подробнее см. гл. 12).
Заданы различные напряжения по концам линии, на- пример (рис. 3.15, е). Известны мощности нагрузок , , сопротивления участков линии . Надо найти по- токи .
В соответствии с известным из теоретической электро- техники принципом наложения линию на рис. 3.15, е мож- но заменить двумя линиями на рис. 3.15, ж, з, а потоки мощности в исходной линии можно получить в результате наложения (суммирования) потоков в этих линиях. Пото- ки мощности в линии с равными напряжениями по концам на рис. 3.15, ж определяются выражениями (3.73), (3.74). В линии на рис. 3.15,з в направлении от источника пита- ния с большим напряжением к источнику с меньшим на- пряжением протекают сквозной уравнительный ток и уравнительная мощность :
(3.81)
Соответственно в результате наложения потоков, опре- деленных по выражениям (3.73), (3.74) и (3.81), определя- ются потоки мощности в линии с двухсторонним питанием на рис. 3.15, е:
; (3.82)
. (3.83)
Определение потерь мощности осуществляется так:
.
Расчет с учетом потерь мощности. Рассмотрим линию с двухсторонним питанием, к которой преобразуется прос- тая замкнутая сеть (рис. 3.16, а). Мощности ,,
Рис. 3.16. Распределение потоков мощности в замкнутой сети с учетом потерь мощности:
а—исходная сеть; б—представление исходной сети в виде двух линий; в—услов- ные обозначения для расчета потоков в линиях с учетом потерь мощности; г—на- правления потоков в случае несовпадения точек потокораздела активной и реак- тивной мощностей; д—разделение сети при несовпадающих точках потокораздела
определим сначала без учета потерь по выражениям (3.73), (3.74), (3,71). Предположим, что направления мощностей соответствуют точке потокораздела в узле 3, который от- мечен залитым треугольником. «Разрежем» линию в узле 3 (рис. 3.16, б) и рассчитаем потоки мощности в линиях 13 и 43', как это делалось для разомкнутых сетей.
На участке 23 потери активной мощности
;
потери реактивной мощности
,
потери полной мощности
.
Находим значение потока мощности в начале участ- ка 23 (рис, 3.16,в):
.
Далее расчет потоков мощности на участке 12 проводится как для разомкнутых сетей (1-й этап в § 3.6).
Может оказаться, что 1-й этап расчета кольцевой сети выявит две точки потокораздела: одну — для активной, а другую — для реактивной мощности. Такой случай ил- люстрируется на рис. 3.16, г, где узел 2—точка потоко- раздела для активной, а узел 3 — для реактивной мощ- ности.
В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии. Вычислим предварительно потери мощности на участке между точками потокораздела:
;
.
Если теперь принять, что в точке 2 включена нагрузка
,
а в точке 3 — нагрузка
.
где , , , определяются по (3.73), (3.74), а , —по (3.71), то при дальнейшем расчете можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на рис. 3.16, д.
Пример 3.10. Определим мощность, поступающую с шин электро- станции в сеть, рассмотренную в примере 3.9. Расчет проведем с учетом потерь мощности.
Мощности ,, (рис. 3.16, а) определены без учета потерь в примере 3.9. «Разрежем» линяю с двухсторонним питанием в узле 3 потокораздела, как на рис. 3.16,б. Нагрузки в узлах 3 и 3' равны МВА,МВА. Рассчитаем потоки мощности в линиях 23, 12 (рис. 3.16, в).
Мощность в конце линии 23 МВА. Потери мощности в линии 23
МВА.
Мощность в конце линии 12
МВА.
Потери мощности в линии 12
МВА.
Мощность в начале линии 12 .
МВА.
Рассчитаем потоки мощности в линии 43 (рис. 3.16,е). Мощность в конце линии 43 МВА. Потери мощности в ли- нии 43
МВА.
Мощность в начале линии 43
МВА.
Мощность, потребляемая с шин электростанции,
МВА.
Распределение напряжений в линии с двухсторонним питанием. Рассмотрим схему линии с двухсторонним пита- нием от источников 1 и 4 на рис. 3.17, а. Линия питает две
Рис. 3.17. Расчет напряжений в линии с двухсторонним питанием:
а—распределение потоков мощности; б—«разрезание» линии в точке потокораз- дела; в—отключение линии 34; г— отключение линии 12; д—линия с ответвлением
нагрузки —2 и 3. Раздел мощностей предположим в уз- ле 3.
Разрежем линию в узле 3 (рис. 3.17, б) Теперь можно определить напряжения или в двух разомкнутых се- тях, т. е. в линиях 13 и 43'. Если напряжение начала линии равно напряжению конца линии (), то . Если , то и .
Рассмотрим послеаварийные режимы линии. Наиболее тяжелые из них — выход из строя и отключение участков 12 или 34. Проанализируем каждый из режимов и опреде- лим наибольшую потерю напряжения . В послеаварий- ном режиме, когда отключен участок 43 (рис. 3.17, в), обо- значим наибольшую потерю напряжения . В после- аварийном режиме, когда отключен участок 12 (рис. 3.17, г), наибольшую потерю напряжения обозначим . Надо сравнить ии определить наи- большую потерю напряжения . Если линия с двух- сторонним питанием имеет ответвления (рис. 3.17, д), то определение наибольшей потери напряжения усложняется. Так, в нормальном режиме надо определить потери напря- жения ,,, сравнитьих и определить . Чтобы определить в послеаварийном режиме , надо рассмотреть аварийные отключения головных участков 12 и 43.
Пример 3.11. Определим напряжения в узлах 2, 3, а также для сети рис. 3.15, и, рассмотренной в примерах 3.9 и 3.10, используя потоки мощностей, определенные ранее без учета потерь мощности и при их учете.
Расчет напряжении и безучета потерь мощности, т. е. по по- токам мощности, найденным в примере 3.9, проведем также и без учета поперечной составляющей падения напряжения. При кВ потери напряжения и напряжения таковы:
кВ;
кВ;
кВ;
кВ;
кВ;
кВ.
Наибольшая потеря напряжения в нормальном режиме, определяе- мая без учета потерь мощности,
кВ.
Определим напряжения и с учетом потерь мощности, т. е. по потокам мощности, найденным в примере 3.10:
кВ
кВ;
кВ;
кВ;
кВ;
кВ;
кВ.
Таким образом, кВ.
Погрешность расчета наибольшей потери напряжения равна
кВ.
Рассмотрим послеаварийные режимы (рис. 3.17,в и г).
При отключении линии 43 мощность в линии 12 (рис. 3.17,в)
МВА.
Мощность в линии 23
МВА.
Определим потери напряжения в линиях 12, 23, напряжения в узлах 2,3 и :
кВ;
кВ;
кВ;
кВ;
кВ.
studfiles.net
5. Расчет потерь электрической энергии
В ЭЛЕМЕНТАХ СЕТИ
5.1. Потери электроэнергии в сети напряжением 10 кВ системы
одно- и двухстороннего питания
Потери электроэнергии в различных элементах сети пропорциональны квадрату тока (или мощности), протекающего через эти элементы, а также сопротивлению элементов. В линии, выполненной из проводов одинакового сечения по всей длине, потери электроэнергии, кВт·ч,
, (38)
где τi– время максимальных потерь электрической энергии для участка с номером i или условное время, в течение которого в линии, работающей с максимальной нагрузкой, выделяются те же потери энергии, как и при работе по действительному графику I(t) за год.
Учитывая, что время использования максимума активной нагрузки Тmaxзадано для всех потребителей одно и то же, в работе можно принять τi одинаковым для всех участков.
Время максимальных потерь можно найти по эмпирической формуле [1], ч:
. (39)
Потери электроэнергии в трансформаторах подстанций определяются потерями холостого хода и короткого замыкания по формуле, кВт·ч:
, (40)
где t – время, в течение которого трансформатор находится в работе (принять t равным 8760 ч).
Суммарные потери в сети 10 кВ для вариантов одно- и двухстороннего питания, кВт·ч,
. (41)
5.2. Мероприятия по снижению потерь мощности и электроэнергии
По своей физической сущности, с точки зрения производства, передачи и потребления, потери электроэнергии ничем не отличаются от энергии, полезно отпущенной потребителям. Основным экономическим показателем при оценке потерь является стоимость электроэнергии. Потери электроэнергии оказывают существенное отрицательное влияние на технико-экономические показатели сети, так как их стоимость включается и в приведенные затраты, и в годовые эксплуатационные расходы.
Необходимо отчетливо представлять, что любое техническое мероприятие, направленное на снижение потерь, требует затрат, и поэтому речь должна идти не о всемерном их снижении, а о достижении оптимального уровня потерь. Ведь увеличение стоимости сети почти всегда приводит к снижению потерь, и наоборот, в случае меньших капиталовложений потери растут. Проектирование сетей ведется обычно таким образом, чтобы обеспечить оптимальное соотношение между затратами на сеть и потерями электроэнергии. Однако со временем в связи с ростом нагрузок потери электроэнергии увеличиваются, и это соотношение не сохраняется. Отсюда вытекает необходимость контроля за потерями и расчета потерь как одного из важнейших показателей экономич-ности работы сети.
Все мероприятия по снижению потерь можно разбить на две группы: организационные и технические.
Организационные мероприятия не требуют существенных дополнительных затрат труда, материалов или денежных средств, например, повышение уровня напряжения путем его регулирования существующими средствами, сокращение сроков и повышение качества ремонта оборудования энергосистем, отключение на предприятиях в ночное время и праздничные дни большинства силовых трансформаторов, выравнивание годовых и суточных графиков нагрузок при том же электропотреблении и др.
Выравнивание графиков нагрузок направлено на упорядочение технологических процессов производства и повышение их ритмичности, приводит к существенному снижению потерь активной мощности и электроэнергии, а также к уменьшению суммарного максимума нагрузки энергосистемы. При этом уменьшается потребность в электростанциях.
Организационные мероприятия по снижению потерь бесспорны по своей целесообразности и не нуждаются в дополнительном обосновании.
На технические мероприятия требуются, как правило, существенные дополнительные затраты. Сводятся эти мероприятия к следующему: перевод сети на более высокое номинальное напряжение, применение проводов большей площади сечения (снижение сопротивления), замена перегруженных и недогруженных трансформаторов (также снижение сопротивления), установка компенсирующих устройств – так называемая компенсация реактивной мощности.
Целесообразность технических мероприятий по снижению потерь должна обосновываться соответствующими экономическими расчетами.
studfiles.net
5. ПОТЕРИ МОЩНОСТИ И ЭНЕРГИИ В ЭЛЕКТРИЧЕСКИХ СЕТЯХ
Режимные трудности усугубляются тем, что в настоящее время структура генерирующих мощностей меняется в сторону снижения маневренности, это связано с вводом в эксплуатацию крупных блоков. Для покрытия пиков нагрузки энергосистем приходится привлекать к переменным режимам работы блоки мощностью 200—300МВт на газомазуте, которые на это не рассчитаны. В отдельные дни электростанция мощностьюуст = 18 ГВт выдает до1,2—1,5ГВт.
Около 50 % времени в году блоки эксплуатируются при нагрузках 40 % от номинальной мощности. При такой эксплуатации оборудования блоков снижается их экономичность. Снижение нагрузки энергосистем в воскресные дни приводит к необходимости отключения части блоков (20—25раз в году), что в свою очередь повышает аварийность оборудования, так как велика вероятность отказа блока при пуске (до 0,4).
Исследования показали, что проблема покрытия графика нагрузки энергосистемы может быть решена только комплексно ––путем увеличения маневренности оборудования; сооружения пиковых электростанций; внедрения специальных блоков повышенной маневренности на газомазуте мощностью 500 МВт, использования газотурбинных станций; сооружения гидроаккумулирующих электростанций, введения режимных мероприятий, объединения энергосистем в единую ЭЭС РФ.
Контрольные вопросы
1.Каковы способы представления нагрузки как динамической характеристики?
2.Что такое типовые графики нагрузки? Какие графики используются в качестве типовых?
3.Каковы основные показатели графиков нагрузки? Разъяснить их смысл.
4.Как строится график нагрузки по продолжительности?
5.Назовите характерные показатели графиков нагрузок.
6.Как определяются показатели нагрузки узла сети по данным отдельных потребителей?
7.Как определяются показатели нагрузки системы по данным нагрузок подсистем?
8.Какие характерные зоны выделяют в графиках нагрузки?
Передача электроэнергии сопровождается потерями активной и реактивной мощности и энергии. Потерянная энергия расходуется на нагрев проводов ЛЭП, обмоток, корпуса и сердечников трансформаторов.
Потери активной мощности связаны с необходимостью установки дополнительной мощности генераторов и дополнительными расходами топлива, следовательно, дополнительными затратами на компенсацию потерь. Потери активной мощности в электрических сетях составляют от 2 до 6 % мощности нагрузок.
Потери реактивной мощности в элементах электрических сетей приводят к возрастанию потерь активной мощности, обусловливают установку дополнительных компенсирующих устройств, что также связано с дополнительными затратами. Потери реактивной мощности в электрических системах в несколько раз больше потерь активной мощности, это объясняется соотношением актив-
ных и реактивных сопротивлений элементов электрических систем ( | ). |
35 |
|
Величина потерь реактивной мощности в элементах электрических систем составляет от 6 до 12 % мощности нагрузок [5].
Уровень потерь как активной, так и реактивной мощности зависит от класса напряжения сети и уменьшается с увеличением класса напряжения [1, 3, 4].
5.1. Потери мощности в участке сети
Рассмотрим участок сети, схема замещения которого показана на рис. 5.1. Обозначения, принятые на рисунке, следующее: — сопротивление,
— проводимости схемы замещения, которые считаем заданными;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| — | поток |
|
|
| н |
|
| к |
|
|
|
|
|
|
|
| 3 |
|
|
| |||||
|
|
|
|
|
|
|
|
|
| мощности нагрузки, если | |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
| н |
|
| к |
|
|
| трехфазной |
|
| √ |
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
| в конце участка подключен потреби- | |||||||||||||||
|
|
| ∆ |
|
|
| |||||||||||||||||
|
|
| ш |
|
| ш | тель, имеющий индуктивный харак- | ||||||||||||||||
|
|
|
|
| |||||||||||||||||||
ш |
|
| ш |
| тер, то | 0 | . Аналогично для пото- | ||||||||||||||||
|
| ∆ ш |
|
| ∆ ш | ка |
|
|
| 3 |
| . | Везде | рас- | |||||||||
|
|
|
|
|
|
|
|
|
|
|
| мощности, | втекающей в | сеть | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
| сматриваются |
| линейные напряжения | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| √ |
|
|
|
|
|
|
|
| |||
|
| Рис. 5.1. Схема замещения сети | и фазные токи. Начало и конец уча- | ||||||||||||||||||||
|
| стка обозначены «н» и «к», |
| ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
| н | н | н | √ |
| ; | к | к | к |
|
| √ |
| . |
| (5.1) | ||||
|
| 3 |
|
| 3 |
| |||||||||||||||||
Здесь н ик ––соответственно потоки мощности в начале и конце сопротивления .
|
|
| ∆ ш | 3 ш |
| 1 | , |
|
|
| (5.2) | ||
|
|
|
|
|
|
| |||||||
с учетом того, что |
|
| ш |
|
|
| |||||||
|
|
|
| 1 |
|
|
| 1 |
| ||||
| ш | ш ш , ш | ш | ш | √ |
|
| , | ш | ш ш | √ |
| , |
получаем | 3 | 3 | |||||||||||
|
|
| ∆ ш |
|
|
|
| , |
|
|
|
|
|
где ∆ ш , = 1, 2 — потери мощности в шунтах схемы замещения.
Потери мощности в шунтах (5.2) не зависят от токов (потоков), передаваемых через участок сети, поэтому называются постоянными потерями.
На основании первого закона Кирхгофа для узлов 1 и 2 можно записать
| к | ∆ | ш ; | в | н | ∆ | ш . | (5.3) |
|
|
|
| |||||
Напротив, потери мощности |
|
| сопротивлении | пропорциональны | ||||
квадрату тока (потока), поэтому | они называются переменными потерями. Для | |||||||
| ∆ |
|
|
|
|
| ||
их определения используются следующие соотношения: |
| |||||||
∆ | 3 | 3 | 36 | 3 | ∆ |
| . | (5.4) |
Учитывая, что 3 | н ⁄ | к ⁄ | , имеем |
| ||
| ∆ | н |
| к |
| |
|
|
|
| . | (5.5) | |
Так как | ; |
|
| , a | , то выражение для | |
переменных потерь мощности может быть представлено в различных формах, например
к к н н
∆ ; ∆.
Следует обратить внимание, что потери мощности могут быть определены по данным как начала, так и конца участка — важно использовать напряжения и потоки мощности для одной и той же точки участка («к» или «н»).
Для связи потоков и потерь можно использовать следующие выражения:
н |
|
| к | ∆ |
| ; | ш |
|
| (5.6) | |||
|
|
|
|
|
|
|
| . |
| (5.7) | |||
|
|
|
|
|
|
| ш |
|
|
|
| ||
5.2. Потери мощности в | линии электропередачи |
| |||||||||||
∆ |
|
|
| ∆ |
|
|
| ∆ |
|
|
|
| |
Линия электропередачи имеет |
| схему | замещения, | как на | рис. 5.1, где | ||||||||
; |
|
| 2 |
|
|
|
| 2 . Тогда потери в шунтах ли- | |||||
нии, имеющих емкостный характер, | равны |
|
|
| ⁄ |
|
|
|
| ||||
| ⁄ |
|
|
|
|
|
|
| |||||
∆ ш |
|
|
|
|
|
|
|
|
| ∆ ш | ∆ ш . | (5.8) | |
|
| 2 |
|
|
| 2 |
| ||||||
Активные потери в шунтах ∆ ш определяются потерями на корону, а реактивная составляющая∆ ш определяется емкостной генерацией линии. Обычно для расчетов потери активной мощности на корону в ЛЭП принимают равными средним удельным потерям∆ кор.ср и определяют из справочников [5, табл.
7.7]. С учетом числа параллельных | линий и длины ЛЭП | ℓ | потери в шунтах | |||||||
1 |
|
|
|
| ||||||
1 |
|
|
| 2 | ∆ кор.max |
| ∆ кор.min |
| ||
∆ ш |
| ∆ кор.ср | ℓ |
| 2 | ℓ . | ||||
2 |
| |||||||||
Переменную составляющую потерь мощности можно определить по введенным ранее формулам (5.5).
Вприближенных расчетах, когда неизвестны точные значения напряжений
вузлах электрической сети, потери мощности можно определять по прибли-
женным (средним) значениям напряжений .
5.3. Потери мощности в трансформаторах
Схема замещения двухобмоточного трансформатора отличается от схемы замещения рис. 5.1 только тем, что = 0, поэтому введенные ранее выражения для вычисления потерь также справедливы для трансформаторов.
37
Для приближенных расчетов постоянную составляющую потерь в транс-
форматоре (потери в стали |
|
|
|
|
|
|
|
| ) можно считать равной потерям | ||||
холостого хода. При этом | предполагается, что напряжение на трансформаторе | ||||||||||||
∆ | ст | ∆ | ст |
| ∆ | ст |
|
|
|
| |||
примерно равно номинальному. |
|
|
|
|
|
|
|
|
|
| |||
Для подстанции с параллельными трансформаторами эквивалентные по- | |||||||||||||
тери | ∆ ш.э |
| ∆ ст.э |
| ∆ х.х |
| ∆ х.х |
|
| ||||
Если учитывать |
|
|
| . | (5.9) | ||||||||
|
|
|
|
| |||||||||
писать | отклонение напряжения от номинального, то следует за- | ||||||||||||
∆ ш.э | ∆ ст.э | ∆ х.х |
|
|
|
|
|
| |||||
|
|
|
| . |
| (5.10) | |||||||
|
|
|
|
| |||||||||
Переменная составляющая активных | потерь в | параллельно включенных | |||||||||||
|
| ном |
|
| |||||||||
трансформаторах (потери в меди) в соответствии с (5.4) может быть определена по формуле
|
|
|
|
|
|
|
|
|
| 3 |
|
| . |
|
|
|
|
|
| ||
Учитывая, что для | двухобмоточных трансформаторов |
| |||||||||||||||||||
|
|
|
|
|
| ∆ м.э |
|
|
|
| э |
|
|
|
|
|
|
| |||
| э | 1 |
| 1 | ∆ к.з | ном | , |
| а 3 |
|
|
|
| , | |||||||
|
|
|
|
|
|
|
|
|
| ||||||||||||
получаем |
|
|
|
|
|
| ном |
|
|
|
|
|
|
|
|
| |||||
|
| ∆ м.э |
| 1 | ∆ к.з |
|
|
|
|
|
| ном | . | (5.11) | |||||||
|
|
|
|
|
|
|
|
| |||||||||||||
Полагая в приближенных расчетах ном |
| ном | , имеем |
| |||||||||||||||||
|
|
|
| ∆ | 1 | ∆ к.з |
|
|
|
|
|
| |||||||||
|
|
|
|
| м.э |
|
|
| . | (5.12) | |||||||||||
|
|
|
|
|
| ном | |||||||||||||||
При определении потерь мощности в трехобмоточных трансформаторах и автотрансформаторах следует учитывать загрузку каждой из обмоток трансформаторов и потери короткого замыкания каждой из обмоток:
1 |
|
| в | 1 |
|
| с | 1 |
|
| н | , | (5.13) | |||
|
|
|
|
|
|
|
|
|
|
|
| |||||
∆ м.э | ∆ |
|
| ∆ |
|
| ∆ | |||||||||
кв.зном |
|
| кс.зном |
|
| кн.зном |
|
| ||||||||
где — число трансформаторов;в,с,н — потоки мощности по обмоткам высшего, среднего и низшего напряжения соответственно;∆ кв.з,∆ кс.з,∆ кн.з — потери короткого замыкания обмоток;ном — номинальная мощность трансформатора.
5.4. Потери энергии в элементах электрических сетей
Величина потерь электроэнергии зависит от потерь мощности и времени работы сети. Рассмотрим передачу мощности через трансформатор (рис. 5.2).
38
Если нагрузка участка сети остается посто- |
|
|
|
| ||||
янной в течение времени | , | то выделив- |
|
|
|
| ||
|
|
|
| |||||
шиеся потери энергии | ∆Эи | можно опреде- |
|
|
|
| ||
|
|
|
| |||||
|
|
|
| |||||
лить как произведение |
| : |
|
|
|
|
| |
| ∆ | . | (5.14) |
| Рис. 5.2. Схема участка сети | |||
|
| |||||||
случаях нагрузки потре- |
| |||||||
|
|
|
| |||||
В реальных∆Э | ∆ |
|
|
|
|
|
|
|
бителей не остаются постоянными, а меняются в соответствии с графиком нагрузки (рис. 5.3, а). Тогда переменная составляющая потерь активной мощно-
сти | для каждого момента времени определяется в зависимости от квад- | |
рата∆мощности нагрузки (потока через сопротивление | ): | |
|
|
|
| ∆ |
| 1 |
| . |
|
|
|
| |
,% |
|
| а |
| ,% |
| б | 2 |
|
| |||
|
|
|
|
|
| 100 |
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
| |
80 |
|
|
| 2 |
|
| 80 |
|
|
|
|
|
|
60 |
|
| max |
|
|
| 60 |
|
| max |
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| |||
40 |
|
|
|
| 1 |
|
|
|
|
| |||
|
|
|
| 40 |
|
|
|
|
| ||||
20 |
|
|
| max |
|
| 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
0 |
|
|
|
| , ч |
|
|
|
|
| , ч | ||
|
|
|
|
|
|
|
|
|
|
| |||
∆ ,% | 4 | 8 | 12 | 16 | 20 | 24 | 0 | 4 | 8 | 12 | 16 | 20 | 24 |
|
| в |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
80 |
|
|
| 2 |
|
|
|
|
|
|
|
|
|
60 |
| ∆ max |
|
|
|
|
|
|
|
|
|
| |
40 |
|
|
| 1 |
|
|
|
|
|
|
| ||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| t, ч |
| Рис. 5.3. График нагрузки: |
| |||
0 | 4 | 8 | 12 | 16 | 20 | 24 |
|
|
| ||||
| 1 – действительный; 2 – ступенчатая линеаризация | ||||||||||||
На рис. 5.3, а показан график нагрузки в процентах от | , на рис. 5.3, б | ||||
— график квадратичной нагрузки в процентах от | max, |
| 5.3, в — график | ||
потерь активной мощности в процентах от | . | на рисmax. | |||
| 5.3, б,в совпадает, если не учиты- | ||||
Заметим, что конфигурация графиков∆ max |
|
|
|
| |
вать изменение напряжения | при изменении нагрузки | . Площадь под кривой | |||
| за время | : |
|
|
|
∆ представляет собой потери энергии39 |
|
|
|
| |
studfiles.net













Поделиться с друзьями: