Когда конденсатор подключен к переменному синусоидальному напряжению, в нем возникает синусоидальный ток, опережающий напряжение на 90о(рис. 4.5.1). Рис. 4.5.1 Мгновенная мощность, потребляемая конденсатором (как и любой другой цепью) определяется как произведение напряжения и тока: p = ui График изменения этой мощности можно построить, перемножая попарно ординаты графиков u(t) иi(t), взятые в один и тот же момент времени. Полученная таким образом кривая (рис. 4.5.1) представляет собой синусоиду двойной частоты с амплитудой. QC = UCm ICm /2 = UC IC. Когда p>0, конденсатор заряжается, потребляя энергию и запасая ее в электрическом поле. Когдаp<0, он отдает ее другим элементам цепи, являясь источником энергии. ВеличинаQCявляется максимальной мощностью, потребляемой или отдаваемой конденсатором, и называетсяемкостной реактивной мощностью. Средняя (активная) мощность, потребляемая конденсатором, равна нулю. Выведите кривые тока и напряжения конденсатора на экран виртуального осциллографа, перенесите их на график и постройте кривую изменения мгновенных значений мощности перемножением мгновенных значений напряжения и тока. Соберите цепь согласно схеме (рис. 4.5.2), подсоедините к ней регулируемый источник синусоидального напряжения с параметрами: U = 5Bиf= 1 кГц. Рис. 4.5.2 Установите параметры развёртки осциллографа так, чтобы на экране было изображение примерно одного-двух периодов напряжения и тока. Включите блок «Приборы II», выберите из меню функции «Активная мощность» и «Реактивная мощность», подключите их кV1 иA1, запишите значения реактивной мощностиQCи убедитесь, что активная мощность близка к нулю. Занесите данные осциллографирования напряжения и тока конденсатора в табл. 4.5.1 соответственно указанным моментам времени. Выполните вычисления мгновенных значений мощности. Таблица 4.5.1 Время t, мс ТокiC, мА Напряжение uC, В p = uCiC, мВт 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 Рис. 4.5.3 По графику p(t) определите максимальное значение (реактивную мощность) и сравните ее с реактивной мощностью, измеренной варметром. По осциллограмме: QC= …… мВт; По варметру: QC= …… ВАр. studfiles.net В том случае, если обкладки заряженного конденсатора замыкают при помощи проводника, то в проводнике появляется электрический ток, и через некоторое время конденсатор разряжается. При прохождении тока по проводнику выделяется некоторое количество теплоты, следовательно, конденсатор, обладающий зарядом, имеет энергию. Определим энергию заряженного конденсатора. Будем считать, что конденсатор заряжают и этот процесс происходит очень медленно. Мгновенное значение напряжения между его обкладками обозначим как u. Так как процесс зарядки считаем квазистатическим, между обкладками увеличивается бесконечно медленно. Тогда потенциал каждой обкладки в каждый момент времени можно считать одинаковым в любом месте обкладки. При увеличении заряда обкладки на величину dq, совершается внешняя работа (работа источника) равная Используем формулу, которая связывает заряд, емкость и напряжение, получим: В том случае, если емкость не зависит от напряжения электрического поля, то работа Применяя формулу: выражение для энергии поля конденсатора можно преобразовать к виду: Именно благодаря своей способности запасать энергию, конденсаторы имеют большое значение в радиотехнике и электронике. Напряжение между обкладками плоского конденсатора может быть найдено как: где d — расстояние между пластинами конденсатора. Учитывая, что для плоского конденсатора емкость определена выражением: имеем: где ru.solverbook.com Если два заряда сообщить двум изолированным проводникам, то между ними возникнет так называемая разность потенциалов, которая зависит от величины этих зарядов и от геометрии проводников. В том случае, если заряды одинаковы по величине, но противоположны по своему знаку, можно ввести определение электрической емкости, из которой потом можно получить такое понятие, как энергия конденсатора. Электрическая емкость системы, состоящей из двух проводников, это отношение одного из зарядов к разности потенциалов между данными проводниками. Энергия конденсатора напрямую зависит от емкости. Можно определить с помощью расчетов это соотношение. Энергия конденсатора (формула) будет представлена цепочкой: W= (C*U*U)/2 = (q*q)/(2*C) = q*U/2 , где W- энергия конденсатора, С- емкость, U- разность потенциалов между двумя пластинками (напряжение), q- значение величины заряда. Значение величины электрической емкости зависит от размеров и формы данного проводника и от диэлектрика, который разделяет эти проводники. Систему, при которой электрическое поле сосредоточено (локализировано) только в некоторой области, называют конденсатором. Проводники, которые составляют это устройство, носят название обкладок. Это простейшая конструкция так называемого плоского конденсатора. Самый простое устройство – это две плоские пластины, обладающие способностью проводить электрический ток. Данные обкладки расположены параллельно на некотором (сравнительно маленьком) расстоянии друг от друга и разделены слоем определенного диэлектрика. Энергия поля конденсатора в таком случае будет локализирована в основном между пластинами. Однако возле краев обкладок и в некотором окружающем пространстве все же возникнет достаточно слабое излучение. Его называют в литературе полем рассеяния. В большинстве случаев принято пренебрегать им и полагать, что вся энергия конденсатора расположена полностью между обкладками. Но в некоторых случаях его все же учитывают (в основном это случаи использования микроемкостей или, наоборот, сверхъемкостей). Электрическая емкость (следовательно, энергия конденсатора) напрямую зависит от пластин. Если посмотреть на формулу C= E0*S/d, где C- ёмкость, E0- величина значения такого параметра, как диэлектрическая проницаемость (в данном случае вакуума) и d- значение расстояния между пластинами, то можно сделать определенный вывод, что емкость такого плоского конденсатора будет обратно пропорциональна величине значения расстояния между этими пластинами и прямо пропорциональна их площади. Если же пространство между обкладками заполнить каким-то определенным диэлектриком, то энергия конденсатора и его емкость увеличатся в E раз (E в данном случае - диэлектрическая проницаемость). Таким образом, теперь можно выразить и формулу потенциальной энергии, которая накапливается между двумя обкладками (пластинами) конденсатора: W=q*E*d. Однако гораздо проще выражать понятие "энергия конденсатора" через емкость: W=(C*U*U)/2. Формулы параллельного и последовательного соединения остаются верными при любом числе конденсаторов, соединенных в батарею. fb.ru Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками. В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах. Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид где — заряд, — потенциал проводника. Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (еёдиэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ): Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком —конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна: где S — площадь одной обкладки (подразумевается, что они равны), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная. Конденса́тор (от лат. condensare — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённыхдиэлектриком, толщина которого мала по сравнению с размерами обкладок. Виды конденсаторов: 1. по виду диэлектрика: воздушные, слюдяные, керамические, электролитические 2. по форме обкладок: плоские, сферические. 3. по величине емкости: постоянные, переменные (подстроечные). Электроемкость плоского конденсатора где S - площадь пластины (обкладки) конденсатора d - расстояние между пластинами eо - электрическая постоянная e - диэлектрическая проницаемость диэлектрика Включение конденсаторов в электрическую цепь параллельное последовательное ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА Конденсатор - это система заряженных тел и обладает энергией. Энергия любого конденсатора: где С - емкость конденсатора q - заряд конденсатора U - напряжение на обкладках конденсатора Энергия конденсатора равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или равна работе по разделению положительных и отрицательных зарядов , необходимой при зарядке конденсатора. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ КОНДЕНСАТОРА Энергия конденсатора приблизительно равна квадрату напряженности эл. поля внутри конденсатора. Плотность энергии эл. поля конденсатора: 13. studfiles.net С момента начала изучения электричества решить вопрос о его накоплении и сохранении удалось лишь в 1745 году Эвальду Юргену фон Клейсту и Питеру ван Мушенбруку. Созданное в голландском Лейдене устройство позволяло аккумулировать электрическую энергию и использовать ее при необходимости. Лейденская банка – прототип конденсатора. Ее использование в физических опытах продвинуло изучение электричества далеко вперед, позволило создать прототип электрического тока. Собирать электрический заряд и электроэнергию – основное назначение конденсатора. Обычно это система из двух изолированных проводников, расположенных как можно ближе друг к другу. Пространство между проводниками заполняют диэлектриком. Накапливаемый на проводниках заряд выбирают разноименным. Свойство разноименных зарядов притягиваться способствует большему его накоплению. Диэлектрику отводится двойственная роль: чем больше диэлектрическая проницаемость, тем больше электроемкость, заряды не могут преодолеть преграду и нейтрализоваться. Электроемкость – основная физическая величина, характеризующая возможность конденсатора накапливать заряд. Проводники называют обкладками, электрическое поле конденсатора сосредотачивается между ними. Энергия заряженного конденсатора, по всей видимости, должна зависеть от его емкости. Энергетический потенциал дает возможность применять (большая электроемкость) конденсаторы. Энергия заряженного конденсатора используется при необходимости применить кратковременный импульс тока. От каких величин зависит электроемкость? Процесс зарядки конденсатора начинается с подключения его обкладок к полюсам источника тока. Накапливаемый на одной обкладке заряд (величина которого q) принимается за заряд конденсатора. Электрическое поле, сосредоточенное между обкладками, имеет разность потенциалов U. Электроемкость (С) зависит от количества электричества, сосредоточенного на одном проводнике, и напряжения поля: С= q/U. Измеряется эта величина в Ф (фарадах). Емкость всей Земли не идет в сравнение с емкостью конденсатора, величина которого примерно с тетрадь. Накапливаемый мощный заряд может быть использован в технике. Однако накопить неограниченное количество электричества на обкладках нет возможности. При возрастании напряжения до максимального значения может произойти пробой конденсатора. Пластины нейтрализуются, что может привести к порче устройства. Энергия заряженного конденсатора при этом полностью идет на его нагревание. Нагревание конденсатора происходит из-за превращения энергии электрического поля во внутреннюю. Способность конденсатора совершать работу по перемещению заряда говорит о наличии достаточного запаса электроэнергии. Чтобы определить, как велика энергия заряженного конденсатора, рассмотрим процесс его разрядки. Под действием электрического поля напряжением U заряд величиной q перетекает с одной пластины на другую. По определению, работа поля равна произведению разности потенциалов на величину заряда: A=qU. Это соотношение справедливо лишь для постоянного значения напряжения, но в процессе разрядки на пластинах конденсатора происходит постепенное его уменьшение до нуля. Чтобы избежать неточностей, возьмем его среднее значение U/2. Из формулы электроемкости имеем: q=CU. Отсюда энергия заряженного конденсатора может быть определена по формуле: W = CU2/2. Видим, что ее величина тем больше, чем выше электроемкость и напряжение. Чтобы ответить на вопрос о том, чему равна энергия заряженного конденсатора, обратимся к их разновидностям. Поскольку энергия электрического поля, сосредоточенного внутри конденсатора, напрямую связана с его емкостью, а эксплуатация конденсаторов зависит от их конструктивных особенностей, используют различные типы накопителей. В зависимости от типа различают и иные конденсаторы. Энергия заряженного конденсатора зависит от свойств диэлектрика. Основной величиной называют диэлектрическую проницаемость. Электроемкость ей прямо пропорциональна. Рассмотрим простейшее устройство для собирания электрического заряда – плоский конденсатор. Это физическая система из двух параллельных пластин, между которыми находится слой диэлектрика. Форма пластин может быть и прямоугольной, и круглой. Если есть необходимость получать переменную емкость, то пластины принято брать в виде полудисков. Поворот одной обкладки относительно другой приводит к изменению площади пластин. Будем считать, что площадь одной пластины равна S, расстояние между пластинами примем равным d, диэлектрическая проницаемость наполнителя - ε. Электроемкость такой системы зависит только от геометрии конденсатора. С = εε0S/d. Видим, что емкость конденсатора прямо пропорциональна полной площади одной пластины и обратно пропорциональна расстоянию между ними. Коэффициент пропорциональности - электрическая постоянная ε0. Увеличение диэлектрической проницаемости диэлектрика позволят нарастить электроемкость. Уменьшение площади пластин позволяет получить подстроечные конденсаторы. Энергия электрического поля заряженного конденсатора зависит от его геометрических параметров. Используем формулу расчета: W = CU2/2. Определение энергии заряженного конденсатора плоской формы проводят по формуле: W = εε0S U2/(2d). Способность конденсаторов плавно собирать электрический заряд и достаточно быстро его отдавать используется в различных областях техники. Соединение с катушками индуктивности позволяет создавать колебательные контуры, фильтры токов, цепи обратной связи. Фотовспышки, электрошокеры, в которых происходит практически мгновенный разряд, используют способность конденсатора создать мощный импульс тока. Зарядка конденсатора происходит от источника постоянного тока. Сам конденсатор выступает как элемент, разрывающий цепь. Разряд в обратном направлении происходит через лампу малого омического сопротивления практически мгновенно. В электрошокере этим элементом служит тело человека. Способность долгое время сохранять накопленный заряд дает замечательную возможность использовать его в качестве накопителя информации или хранилища энергии. В радиотехнике это свойство широко используется. Заменить аккумулятор, к сожалению, конденсатор не в состоянии, поскольку имеет особенность разряжаться. Накопленная им энергия не превышает нескольких сотен джоулей. Аккумулятор может сохранять большой запас электроэнергии длительно и практически без потерь. fb.ru Конденсатор — это двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля. Список конденсаторов Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки). Изобрел первую конструкцию-прототип электрического конденсатора «лейденскую банку» в 1745 году, в Лейдене, немецкий каноник Эвальд Юрген фон Клейст и независимо от него голландский физик Питер ван Мушенбрук. Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения. При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью, собственной индуктивностью и сопротивлением потерь. Резонансная частота конденсатора равна: fр = 1/ (2∏ ∙ √Lс ∙ C). При f > fp конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f < fp, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной. Отечественные неполярные конденсаторы: На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1·106 пФ = 1·10−6 Ф) и пикофарадах, но нередко и в нанофарадах (1 нФ = 1·10−9 Ф). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 — 180». Основные параметры конденсаторов: Обозначение на схемах: Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др. По виду диэлектрика различают: Вакуумный конденсатор: Кроме того, конденсаторы различаются по возможности изменения своей ёмкости: Два бумажных электролитических конденсатора 1930 года: В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и другие конденсаторы. Серебрянный конденсатор для аудио. Также различают конденсаторы по форме обкладок: ldsound.ru Как любой проводник, несущий заряд, конденсатор имеет энергию, которую находят по формуле: где q – заряд конденсатора; C – емкость конденсатора; Механическую (пондемоторную) силу, с которой пластины плоского конденсатора взаимодействуют между собой можно найти, если использовать формулу (1). Допустим, что расстояние между пластинами конденсатора изменяют от x до При этом потенциальная энергия взаимодействия пластин уменьшается на: Тогда силу, которая выполняет работу можно представить как: Емкость плоского конденсатора равна: Значит, формулу энергии плоского конденсатора запишем как: Подставим в (4) выражение для энергии (6), получим: В выражении (7) минус показывает, что пластины конденсатора притягиваются друг к другу. Если вспомнить, что разность потенциалов между обкладками плоского конденсатора равна: где расстояние меду пластинами конденсатора мы обозначили d, и приняв во внимание, что для плоского конденсатора емкость определена выражением (5) тогда имеем: где ru.solverbook.comКонденсатор. Энергия заряженного конденсатора. Мощность конденсатора
4.5. Реактивная мощность конденсатора
4.5.1. Общие сведения
4.5.2. Экспериментальная часть Задание
Порядок выполнения эксперимента
Энергия конденсатора, теория и примеры
Определение и общие сведения о энергии конденсатора
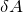 :
:![Rendered by QuickLaTeX.com \[\delta A=udq \qquad (1) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b8c47a81f7533dea59124620dfbd59f4_l3.png)
![Rendered by QuickLaTeX.com \[dq=Cdu\to \delta A=Cudu\ (2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-950def8bf3ab50cbe25138e8779321b8_l3.png)
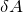 идет на увеличение энергии конденсатора (dW). Проинтегрируем выражение (2), учитывая, что напряжение изменяется от 0 до величины U, имеем:
идет на увеличение энергии конденсатора (dW). Проинтегрируем выражение (2), учитывая, что напряжение изменяется от 0 до величины U, имеем:![Rendered by QuickLaTeX.com \[W=A=C\int^U_0{udu}=\frac{CU^2}{2} \qquad (3) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9c6d20163b409da9176267a8ac8ad42b_l3.png)
![Rendered by QuickLaTeX.com \[q=CU \qquad (4) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-bd8c778807c42012fbcb2caf2baf5158_l3.png)
![Rendered by QuickLaTeX.com \[W=\frac{CU^2}{2}=\frac{qU}{2}=\frac{q^2}{2C} \qquad (5) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-84699b8b8866498e3b519196a72fc967_l3.png)
Энергия поля плоского конденсатора
![Rendered by QuickLaTeX.com \[U=Ed \qquad (6) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1a04f7a0216a59a7827936b4f003bcc4_l3.png)
![Rendered by QuickLaTeX.com \[C=\frac{\varepsilon {\varepsilon}_0S}{d} \qquad (7) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6b1b1baf1f89898f781da708150dab3f_l3.png)
![Rendered by QuickLaTeX.com \[W_p=\frac{\varepsilon {\varepsilon}_0E^2}{2}Sd=\frac{\varepsilon {\varepsilon}_0E^2}{2}V \qquad (8) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1d93ff9f6289fb978a48f3978416653e_l3.png)
 – объем конденсатора; E – напряженность электрического поля в конденсаторе. Объемная плотность энергии (w) может быть найдена как:
– объем конденсатора; E – напряженность электрического поля в конденсаторе. Объемная плотность энергии (w) может быть найдена как:![Rendered by QuickLaTeX.com \[w=\frac{W}{V}=\frac{\varepsilon \varepsilon_0E^2}{2}=\frac{ED}{2} \qquad (9) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3c3598b59325cda49aff218e6e9aa9da_l3.png)
Примеры решения задач
Энергия конденсатора и его емкость



12. Электроемкость. Конденсаторы. Энергия конденсатора. Соединение конденсаторов.
Конденсатор. Энергия заряженного конденсатора
Что такое конденсатор

Электроемкость

Величина энергии
Виды конденсаторов

Плоский конденсатор
Энергия плоского конденсатора
Использование конденсаторов

Конденсатор или аккумулятор

Конденсатор – ldsound.ru









Формула энергии конденсатора, Wp
![Rendered by QuickLaTeX.com \[ W_p=\frac{q\Delta \varphi }{2}=\frac{C{\left(\Delta \varphi \right)}^2}{2}=\frac{q^2}{2C}\ \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0d0a471cdcbe9e2138c913cdd83d6ba5_l3.png)
 – разность потенциалов между обкладками конденсатора.
– разность потенциалов между обкладками конденсатора. Связь энергии конденсатора и силы взаимодействия его пластин
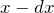 . В таком случае, сила изменяющая расстояние между пластинами выполняет работу, равную:
. В таком случае, сила изменяющая расстояние между пластинами выполняет работу, равную:![Rendered by QuickLaTeX.com \[dA=Fdx\ \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-21afedd09d3b85cd4b5a7432a4201f09_l3.png)
![Rendered by QuickLaTeX.com \[-dW_p=Fdx\ \qquad(3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-dce3670d82de5f5cc81a5ba66c0dfc2f_l3.png)
![Rendered by QuickLaTeX.com \[F=-\frac{dW_p}{dx} \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6080587c445c3cfde34923fbbece5609_l3.png)
![Rendered by QuickLaTeX.com \[C=\frac{\varepsilon {\varepsilon }_0S}{x} \qquad(5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3aed248de6812a0e6b710e7f51331b69_l3.png)
![Rendered by QuickLaTeX.com \[W_p=\frac{q^2}{2\varepsilon \varepsilon_0S}x \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe5460ff69582748fd806e2280210348_l3.png)
![Rendered by QuickLaTeX.com \[F=-\frac{q^2}{2\varepsilon {\varepsilon }_0S} \qquad(7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e70528d25d892bfda13c14c3fd36384a_l3.png)
Энергия электростатического поля плоского конденсатора
![Rendered by QuickLaTeX.com \[\Delta \varphi =Ed\ \qquad(8)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-711c072f98f0af4efe1c90bf92358cb3_l3.png)
![Rendered by QuickLaTeX.com \[W_p=\frac{\varepsilon {\varepsilon }_0E^2}{2}Sd=\frac{\varepsilon {\varepsilon }_0E^2}{2}V\ \qquad(9)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ed16f1b0c45b7f173d282a1938b0ac99_l3.png)
 – объем конденсатора; E – напряженность поля конденсатора. Формула (9) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля.
– объем конденсатора; E – напряженность поля конденсатора. Формула (9) связывает энергию конденсатора с зарядом на его обкладках и напряженностью поля. Примеры решения задач по теме «Энергия конденсатора»
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: