Для уменьшения значения входного (питающего) напряжения используют делитель напряжения на резисторах. В нём, выходное напряжение Uвых зависит от значения входного (питающего) напряжения Uвх и значения сопротивления резисторов. Делитель напряжения – наиболее часто применяемое соединение резисторов. Например, переменный резистор, используемый в качестве регулятора громкости Ваших компьютерных колонок, является делителем напряжения с изменяемыми сопротивлениями плеч, где он выполняет роль ограничителя амплитуды входного сигнала. Значение резистора R2 должно быть приблизительно на два порядка меньше (в 100 раз) сопротивления нагрузки подключаемой к выходу делителя. Если Вам не нужна высокая точность, то эту разницу можно снизить до 10 раз. Используя закон Ома, и пренебрегая малым током нагрузки, делитель напряжения можно описать соотношением: (8) Преобразовывая указанную формулу так, как нам удобно, можно определить:1. Выходное напряжение Uвых по известным значениям входного напряжения Uвх и сопротивлений резисторов R1, R2 : (9) Пример: Необходимо определить выходное напряжение Uвых делителя при известных напряжении источника тока Uвх = 50 В, и значениях R1 = 10 кОм и R2 = 500 Ом. Решение: По формуле вычисляем Uвых = 50 * 500 / (10000 + 500) = 2,38 В. 2. Входное напряжение делителя Uвх , по известным значениям выходного напряжения Uвых и сопротивлений резисторов R1, R2 : (10) Пример: Необходимо определить входное напряжение Uвх делителя при необходимых выходном напряжении Uвых = 4 В, и значениях R1 = 15 кОм и R2 = 3 кОм. Решение: По формуле вычисляем Uвх = 4 * (15000 + 3000) / 3000 = 24 В. 3. Значение R1 по известным значениям входного напряжения Uвх , выходного напряжения Uвых и сопротивления резистора R2 : (11) Пример: С помощью делителя напряжения необходимо получить на нагрузке сопротивлением 50 кОм напряжение Uвых = 10 В от источника напряжением Uвх = 50 В. Решение: Сопротивление резистора R2 должно быть в 100 раз меньше сопротивления нагрузки 50 кОм (см. правило 2). Выполняем это условие: R2 = 500 Ом. По формуле вычисляем R1 = 50 * 500 / 10 – 500 = 2000 Ом = 2 кОм Не забывайте, что сам делитель потребляет ток от источника тока, в соответствии с законом Ома (формула 1): Iдел = Uвх / (R1 + R2) = 50/(2000+500) = 0,02 А (20 мА). Определим рассеиваемую мощность резисторов по формуле (3): Для резистора R1 : P = 0,02 * 0,02 * 2000 = 0,8 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт; Для резистора R2 : P = 0,02 * 0,02 * 500 = 0,2 Вт; по правилу (1) выбираем резистор мощностью P = 0,5 Вт. 4. Значение R1 и R2 по известным значениям входного напряжения Uвх , выходного напряжения Uвых и входного (общего) сопротивления делителя Rобщ , где Rобщ = R1 + R2 : (12) (13) Пример: Определить значения R1 и R2 делителя напряжения, если их сумма R1+R2 = 1кОм, при входном напряжении источника Uвх = 50 В и напряжении на выходе Uвых = 20 В. Решение: По формуле (4) вычисляем R2 = 20 * 1000 / 50 = 400 Ом; По формуле (5) вычисляем R1 = 1000 — 400 = 600 Ом; Не забывайте, что сам делитель потребляет ток от источника тока, в соответствии с законом Ома (формула 1): Iдел = Uвх / (R1 + R2) = 50/(600+400) = 0,05 А (50 мА). Определим рассеиваемую мощность резисторов по формуле (3): Для резистора R1 : P = 0,05 * 0,05 * 600 = 1,5 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт; Для резистора R2 : P = 0,05 * 0,05 * 400 = 1 Вт; по правилу (1) выбираем резистор мощностью P = 2 Вт. Напрашивается законный вопрос: Если есть делитель, значит должен быть и коэффициент деления? Конечно! Но он Вам пригодится лишь тогда, когда вы будете иметь дело с другими элементами, например трансформатором, а не резисторами. В качестве R2 делителя напряжения может применяться сама нагрузка с её внутренним сопротивлением. В таком случае, R2 указанное в формуле, приравняйте к сопротивлению нагрузки Rн, и используйте те же формулы, которые применимы к двум независимым резисторам. Тогда, правило (2) не используется. В следующей статье рассмотрим делитель тока. meanders.ru Здравствуйте, мы продолжаем изучать Arduino! Напомню, что в прошлый раз мы сделали простейший светофор на Arduino, а в этот раз я расскажу о делителях напряжения — о том, как они работают, как их рассчитывать и как их можно использоваться для создания измерительного прибора или какого-либо датчика. Название говорит само за себя — делитель напряжения позволяет имея одно напряжение на входе цепи — разделить его на части. Как он работает? Очень просто! Чтобы собрать делитель напряжения нам понадобиться: Делитель напряжения Взгляните на схему. Допустим, между точками А и С приложено напряжение Up. Согласно второму закону Кирхгофа, вытекающего из закона сохранения энергии и «баланса мощностей» в данной цепи возникнет ток. Второй закон Кирхгофа говорит, что сумма падений напряжения на каждом элементе цепи равно сумме ЭДС в этой цепи. Выразим отсюда ток, протекающий в нашей цепи. Идём дальше! Зная ток, протекающий через резисторы, мы в два счёта находим падения напряжения на этих элементах. Напишу формулу для расчёта падения напряжения на резисторе R1: Аналогично напишите сами для резистора R2 (полезно для понимания). Подсказка: ответ будет тот же, но решение иным. Как мы видим, на первом резисторе падает половина напряжения и вторая половина на втором резисторе. Отсюда следует, что в точке В мы имеем половину напряжения Up, что можно выразить также двумя способами. Первый способ — взять потенциал в точке C (Uc) и прибавить к нему падение напряжения UR2 на резисторе R2. Тут мы полагаем, что потенциал точки С нулевой, а точки А соответствует нашей ЭДС цепи. Второй способ: взять потенциал в точке А и вычесть из него падение напряжения UR1 на резисторе R1 Поскольку резисторы у нас одинаковые, то и результат мы получаем одинаковый — половина ЭДС. Но что будет, если взять резистор R2 = 2R1 = R? Расписываем по аналогии с самого начала и получаем R в правой части сократятся и мы получим потенциал в точке В равный 2/3 от ЭДС. Делители напряжения часто используют для создания измеряющих приборов на основе резисторов, изменяющих своё сопротивление при изменении какого-то одного внешнего параметра. Например, температуры (термистор) или света (фото резистор — в турникетах в метро). Также, можно просто понизить напряжение, например, если вам надо измерить напряжение в цепи +12 В с помощью АЦП микроконтроллера, который может измерять лишь в диапазоне от 0 до +5В. Собираете делитель, так чтобы при максимально возможном напряжении в цепи, в его средней точке напряжение не превышало максимально возможного для АЦП. Однако, стоит помнить, о низкой эффективности такого преобразователя напряжений! Использовать делитель для понижения напряжения в целях питания какого-либо устройства не стОит! Делители применяются там, где нужны очень маленькие токи — например для цифровых входов, работающих на напряжении, а не на токе. Ну вот и всё! В этом посте мы научились собирать и рассчитывать делитель напряжения, а также немного узнали об их применении. В следующем посте мы перейдём от теории к практике и соберём измеритель температуры. Если у вас есть какие-либо вопросы, что-то осталось непонятным или хотите узнать по подробнее, то пишите в комментариях к данному посту. Удачи! zhitenev.ru Что такое делитель напряжения. Схема делитель напряжения
Делитель напряжения | Meanders.ru - практическая электроника
Так как, сопротивление нагрузки влияет на выходное напряжение Uвых делителя, для обеспечения точности делителя напряжения, необходимо выполнять правило (2): Всё о делителях напряжения — Блог Ильи Житенёва (БЖ)
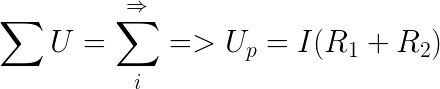
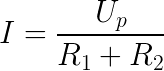

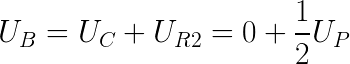
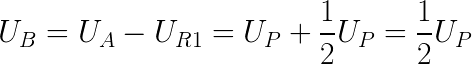
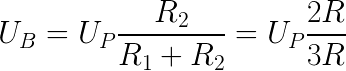
3. Делители тока | 5. Схемы делителей и законы Кирхгофа | Часть1
3. Делители тока
Делители тока
Давайте проанализируем простую параллельную цепь и определим силу тока на каждом из ее резисторов:

Как вы уже знаете, напряжение на всех компонентах параллельной цепи одинаково. Исходя из этого можно заполнить верхнюю строчку рассмотренной ранее таблицы:

Теперь, используя закон Ома (I = U/R), мы можем рассчитать силу тока на каждом резисторе (в каждой ветви):

Один из принципов параллельных цепей гласит, что общая сила тока в таких цепях равна сумме отдельных токов. Поэтому, суммируя 6 мА, 2мА и 3мА, мы можем заполнить ячейку общей силы тока в нашей таблице:

И наконец, вычислим общее сопротивление нашей цепи. Сделать это можно при помощи закона Ома (R = U/I), или при помощи формулы параллельного соединения резисторов. В обоих случаях мы получим одинаковый ответ:

Из данной таблицы видно, что сила тока через каждый резистор связана с его сопротивлением (учитывая равенство напряжений на всех резисторах). Причем взаимосвязь эта обратнопропорциональна. К примеру, сила тока через резистор R1 вдвое больше, чем через резистор R3, хотя сопротивление последнего в два раза превышает сопротивление первого.
Если мы изменим напряжение питания этой схемы, то обнаружим, что пропорциональность соотношений не изменится:

Несмотря на то, что напряжение источника питания изменилось, ток через резистор R1 по-прежнему в два раза превышает ток через резистор R3. Таким образом, пропорциональность между токами различных ветвей цепи является исключительно функцией сопротивления.
Кроме того, токи отдельных ветвей цепи составляют фиксированные пропорции от ее общей силы тока. Несмотря на четырехкратное увеличение напряжения источника питания, соотношение между током любой ветви и общим током осталось неизменным:

Благодаря способности делить общий ток на пропорциональные части, параллельные цепи часто называют делителями тока. Поэкспериментировав немного с математикой, мы можем вывести формулу для расчета отдельных токов цепи, имея данные о сопротивлениях резисторов, общем сопротивлении цепи и общей силе тока:

Отношение общего сопротивления к отдельным сопротивлениям имеет ту же пропорцию, что и отношение отдельных токов к общей силе тока цепи. Полученная выше формула называется формулой делителя тока, с ее помощью легче определять токи отдельных ветвей параллельной цепи, если известна общая сила тока.
Давайте повторно рассчитаем токи каждой из ветвей нашей параллельной цепи, используя только что полученную формулу делителя тока (будем считать, что общая сила тока и общее сопротивление нам известны):

Если сравнить формулы делителя напряжения и делителя тока, то можно увидеть, что они удивительно похожи друг на друга. Однако, в формуле делителя напряжения Rn (отдельное сопротивление) делится на Rобщ., а в формуле делителя тока - наоборот, Rобщ. делится на Rn:

Именно из-за отношения сопротивлений очень легко перепутать эти формулы. В целях избежания путаницы вы должны знать, что отношение сопротивлений в обоих уравнениях должно быть меньше единицы (в конце концов это уравнения делителей, а не умножителей!). Если отношение будет больше единицы, значит вы перепутали уравнения. Зная, что общее сопротивление последовательной цепи (делитель напряжения) всегда больше любого из ее отдельных сопротивлений, Rобщ. мы должны поставить в знаменатель отношения, а Rn - в числитель (только в этом случае отношение будет меньше единицы). И наоборот, зная что общее сопротивление параллельной цепи (делитель тока) всегда меньше любого из ее отдельных сопротивлений, Rобщ. мы должны поставить в числитель отношения, а Rn - в знаменатель.
Схемы делителей токов, как и делителей напряжений, нашли применение в электрических цепях измерительных приборов, где часть измеряемого тока необходимо пропустить через чувствительный прибор:

www.radiomexanik.spb.ru
Резистивный делитель напряжения. Расчет делителя напряжения на резисторах
При проектировании электрических цепей возникают случаи, когда необходимо уменьшить величину напряжения (разделить его на несколько частей) и только часть подавать на нагрузку. Для этих целей используют делители напряжения. Они основаны на втором законе Кирхгофа.
Самая простая схема - резистивный делитель напряжения. Последовательно с источником напряжения подключаются два сопротивления R1 и R2.
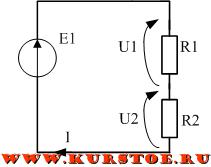
При последовательном подключении сопротивлений через них протекает одинаковый ток I.
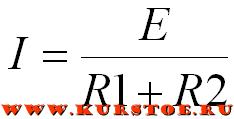
В результате, согласно закону Ома, напряжения на резисторах делится пропорционально их номиналу.


Подключаем нагрузку параллельно к R1 или к R2. В результате на нагрузке будет напряжение равное UR2.
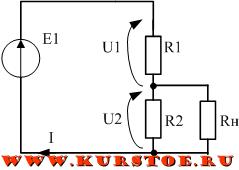
Примеры применения делителя напряжения
- Как делитель напряжения. Представьте, что у Вас есть лампочка, которая может работать только от 6 вольт и есть батарейка на 9 вольт. В этом случае при подключении лампочки к батарейке, лампочка сгорит. Для того, чтобы лампочка работала в номинальном режиме, напряжение 9 В необходимо разделить на 6 и 3 вольта. Данную задачу выполняют простейшие делители напряжения на резисторах.
- Датчик параметр - напряжение. Сопротивление резистивных элементов зависит от многих параметров, например температура. Помещаем одно из сопротивлений в среду с изменяющейся температурой. В результате при изменении температуры будет изменяться сопротивление одного из делителей напряжения. Изменяется ток через делитель. Согласно закону Ома входное напряжение перераспределяется между двумя сопротивлениями.
- Усилитель напряжения. Делитель напряжения может использоваться для усиления входного напряжения. Это возможно, если динамическое сопротивление одного из элементов делителя отрицательное, например на участке вольт-амперной характеристики туннельного диода.
Ограничения при использовании резистивных делителей напряжения
- Номинал сопротивлений делителя напряжения на резисторах должен быть в 100 - 1000 раз меньше, чем номинальное сопротивление нагрузки, подключаемой к делителю. В противном случае сопротивление нагрузки уменьшит величину разделенного делителем напряжения.
- Малые значения сопротивлений, являющихся делителем напряжения, приводят к большим потерям активной мощности. Через делитель протекают большие токи. Необходимо подбирать сопротивления, чтобы они не перегорали и могли рассеять такую величину отдаваемой энергии в окружающую среду.
- Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы, индукционные печи.
- Снижение КПД схемы за счет потерь на активных элементах делителя напряжения.
- Для получения точных результатов в делителе напряжения необходимо использовать прецизионные (высокоточные) сопротивления.
www.kurstoe.ru
Делитель напряжения
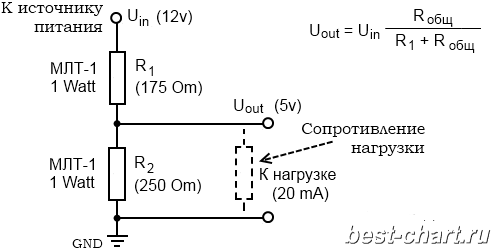
Делитель напряжения применяют с целью получения части напряжения, для отдельных компонентов схемы, используя всего один источник питания.
Принципиальная схема делителя напряжения до элементарного проста и состоит всего из двух резисторов. Главным в ее сборке остается правильный расчет сопротивления резисторов, необходимый для получения конкретного напряжения, и мощности, проходящей через них.
К примеру, для делителя напряжения возьмем сопротивлением исходя из расчетов:
Расчет резисторов для делителя напряжения происходит с конца схемы, а именно имеем изначальные данные: Нагрузка устройства (части компонентов на схеме), для которого рассчитываем делитель напряжения (I) – 20 mA; необходимо получить ток (Uout) – 5 v.
R2 = Uout / I = 5 v / 0.02A = 250 Om;
Зная сопротивление резистора R2, можем найти сопротивление резистора R1:
R1 = Uin / I – R2 = 12 v / 0.02A – 250 Om = 350 Om;
Расчет делителя напряжения окончен, но не все на практике так хорошо, как в теории. Так как нагрузка на выходе делителя напряжения имеет свое сопротивление, расчет необходимо производить с поправкой на это.
Помним, что нагрузка у нас составляет 20 mA, исходя из этого, по закону Ома, рассчитываем сопротивление нагрузки:
Rнагр = U / I = 5 v / 0.02 A = 250 Om;
Как видно, данный расчет мы уже производили выше для резистора R2 делителя напряжения.
В данном случае нагрузка служит параллельным сопротивлением резистору R2, и все расчеты следует поправить, иначе мы потеряем почти 2v:
Rобщ(Rнагр и R2) = Rнагр *R2 / (Rнагр +R2) = 250 * 250 / 250 + 250 = 125 Om;
Uout = Uin( Rобщ / (R1 + Rобщ ) ) = 12 v ( 125 Om / ( 350 Om + 125 Om) ) = 3,16 v;
Исходя из этого, сопротивление резистора R1 необходимо рассчитывать по формуле:
R1 = Uin / Uout * Rобщ – Rобщ = 12 v / 5 v * 125 Om – 125 Om = 175 Om;
Делаем проверку:
Uout = Uin( Rобщ / (R1 + Rобщ ) ) = 12 v ( 125 Om / ( 175 Om + 125 Om) ) = 5 v;
Расчет резисторов необходимых для нашего делителя напряжения закончен, осталось выяснить тип резистора, способный выдержать нагрузку. Рассчитываем мощность, проходящую через резистор делителя напряжения:
P = Uin2 / R1 = 12 v * 12 v / 175 Om ≈ 0,823 Watt;
Делаем вывод, что нам подойдут резисторы, например МЛТ-1 – мощностью не менее 1 Watt.
Применять такого типа делители напряжения можно, только если подключаемая нагрузка потребляет от долей до нескольких десятков миллиампер тока. Данный делитель напряжения никак нельзя использовать для питания мощных приборов, таких как ламп, двигателей и т.д.
Также в качестве эксперимента можно произвести масштабируемость сопротивлений делителя напряжения. Но помните, что чем меньше сопротивление в резисторах делителя напряжения, тем больше на них нагрузка и больше расход энергии.
Делители напряжения удачно подходят для преобразования сигнала с датчиков на основе резисторов. Такие резисторы как фоторезисторы, терморезисторы, тензорезисторы и т.д. способны изменять свое сопротивление в ходе воздействия на них окружающей среды. Подключение такого сенсора к выходу делителя напряжения или вместо одного из резисторов R1 и R2 и вольтметра к точке Uout можно снимать показания.
Страницы:
best-chart.ru
Что такое делитель напряжения
Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.
Что такое делитель напряжения? Формулировка проста – это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.
Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно параллельное и последовательное соединение потребителей. Как известно, при последовательном способе включения сила тока равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два – это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.
Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2. Ток при этом равен (последовательное соединение). Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Чему же равен ток при данных условиях? Обобщая уравнения, получаем:
I = U / (R1+R2).
Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):
U exit = U * R2 / (R1+R2).
Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.
Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин – это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.
Значение сопротивления подключенной нагрузки не должно быть меньше, чем электрическое сопротивление схемы самого делителя, в противном случае всю систему потребуется пересчитывать. В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее падение напряжения, а заниженные будут перегреваться, затрачивая энергию на нагрев.
Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).
fb.ru
Шаг 3. Что такое делитель напряжения?
В самом простом случае делитель напряжения представляет собой два последовательно соединенных резистора (могут быть и конденсаторы - такой делитель будет работать для переменного напряжения). Казалось бы, что тут такого. Но изюминка в том, что можно с его помощью "разделить" напряжение, и получить на выходе напряжение, которое меньше входного. На сколько меньше? Это зависит от трех переменных: напряжения поданного на вход делителя и резисторов R1-R2. Если тебе лень разбираться, можно просто пользоваться формулой выше. А мы пойдём дальше.
Чтобы понять как возможно такое "разделение" напряжения следует вспомнить правила Кирхгофа и что такое падение напряжения на элементе цепи.
Падение напряжения
Это вообще просто. Напряжением же называется разность потенциалов. UR1 =φ1 - φ2. Так вот если измерить напряжение, к примеру, до резистора R1 и после него, то после R1 напряжение будет меньше — оно "упало" (закон Ома!). Поэтому напряжение, измеренное на выводах какого-либо компонента схемы и называют падением напряжения.
Правила Киргофа
Их всего два. Во-первых, в узлах цепи сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Таким образом токи в узлах не теряются — сколько вошло, столько же вышло.
Во-вторых, сумма ЭДС замкнутой цепи равняется сумме падений напряжений вдоль этой цепи. Звучит замудрённо. Для схемы на картинке выше второе правило Кирхгофа будет выполняться так: Uвх = UR1+UR2, — т.е. напряжение никуда просто так не исчезает. Оно "падает" на компонентах цепи и сумма "падений" напряжения будет равна исходному значению напряжения. В нашем случае Uвх.
Вывод формулы
Как я уже говорил, можно просто пользоваться формулой на картинке выше. Она работает. Но тебе же этого мало? Хочется понять почему так?
По первому правилу Кирхгофа следует что через R1, R2 будет протекать один и тот же ток I. Тогда по второму правилу Кирхгофа:
Uвх = UR1+UR2 = I*R1 + I*R2 = I*(R1 + R2). Выразим ток и получим: I = Uвх / (R1 + R2).Пользуясь законом Ома: UR2 = Uвых = I*R2 = Uвх / (R1 + R2) * R2
Всё просто!
Где применять?
Хочется того или нет, делители напряжения используются повсеместно. Но чаще всего специально думать о них не приходиться, кроме тех случаев, когда нужен делитель с определенным коэффициентом деления. Кстати, всем известные переменные резисторы могут использоваться как делители напряжения.
Открою секрет. Есть ещё делители тока. Простейший делитель тока — это два резистора, соединенных параллельно.
mp16.ru










Поделиться с друзьями: