3.3 Соединение звездой. Трехпроводная система трехфазного тока. Трехфазное соединение по схеме звезда образуется если

Соединение фаз потребителей электроэнергии в звезду

Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:

Из схемы видно, что фазные напряжения приемника Ua, Ub, Uc не равны линейным напряжениям Uab, Ubc, Uca. Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:

Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.

Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:

Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.

Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.

Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:

Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:

Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода IN. В случае отсутствия нейтрального провода справедливо будет выражение:

Симметричная нагрузка при соединении приемников звездой

Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:

Условие симметричности также может быть выражено через комплексные сопротивления Za = Zb = Zc.

Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.

В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:

Так как в четырехпроводной цепи Ua = Ub = Uc = Uл /  , то при симметричной нагрузке:

Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше. Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен IN = Ia + Ib + Ic = 0.

Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.

Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.

Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:

Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:

Пример

К трехфазной электрической цепи с линейным напряжением Uл = Uab = Ubc = Uca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление rф = 10 Ом и индуктивное сопротивление хф = 10 Ом, которые соединены последовательно. Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.

Решение

Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.

Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:

Активная, реактивная и полная мощности  приемника, а также любой фазы будут равны:

Векторная диаграмма для данной системы приводилась выше.

Несимметричная нагрузка при соединении приемников звездой

Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: ra = rb = rc, xa = xb ≠ xc. В общем случае  считают, что несимметричная нагрузка возникает при отключении одной из фаз.

Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.

В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.

Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.

Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.

Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:

Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:

Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.

Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).

Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:

Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.

Пример

В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы Uном = 127 В, Рном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.

Решение

Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:

Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:

Для определения тока в нейтральном проводе IN решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:

Где комплексные значения фазных сопротивлений будут равны Za = 8,05 Ом, Zb = 16,1 Ом, Zс = 32,2 Ом.

Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:

elenergi.ru

3.3. Расчет трехфазных цепей при соединении звездой

Для расчета токов должна быть задана схема цепи, значение и тип сопротивлений, напряжение источника энергии. Расчеты обычно проводят для комплексных значений.

Симметричная нагрузка в схеме соединением «звезда – звезда» с нулевым проводом представлена на рис. 4.8.

Рис. 4.8.

Если нулевой провод в схеме симметричного приемника () обладает весьма малым сопротивлением (Z0 = 0), то потенциал точки О/ практически равен потенциалу точки О, и точки сливаются в одну. В схеме образуются три обособленных контура, комплексные значения токов в каждом из которых определяются как в однофазной цепи ; ;

где ĖА, ĖВ, ĖС – фазные напряжения на зажимах генератора.

По первому закону Кирхгофа ток в нулевом проводе 4-х проводной системы равен геометрической сумме фазных токов .

В общем случае комплексное напряжение между нулевыми точками 0 – 0` при наличии нейтрального провода

.

При равномерной симметричной нагрузке ток I0=0, и нулевой провод может быть изъят из схемы без изменения ее режима работы. Для 3-х проводной системы, т.е. не содержащей нейтральный провод (ZN = ∞) слагаемое 1/ ZNв знаменателе будет отсутствовать.

При определении напряжения фаз приемника если не учитывать сопротивления источника, то можно заменить на

Переходя к действующим значениям величин в случае, когда нагрузки во всех фазах равны и имеют активный характер ,

где − значение линейного напряжения, токи соответственно принимают значения,,.

Общая мощность трехфазной цепи с активной нагрузкой равна

.

4.4. Несимметричная нагрузка при соединении звездой

При несимметричной нагрузке и отсутствии нулевого провода между нулевыми точками генератора О и приемника О/ появляется напряжение , в результате чего фазные напряжения приемника оказываются различными. Расчетные соотношениемежду фазными и линейными напряжениями при этом нарушается. Для определения напряжения между нулевыми точками, а также фазных напряжений приемника предположим, что в электрической цепи имеется нейтральный (нулевой) провод, сопротивление которого. Тогда напряжение между нулевыми точками источника и приемника

,

где g A, g B, g C, g N – проводимости фазных и нулевого проводов,

т

Рис. 3. 9. 3.10.

.е. для несимметричной системы при определении в знаменателе учитывается проводимость нейтрального провода gN..

На рис. 4.9. приведена векторная диаграмма без нейтрального провода, на которой ,,− векторы фазных напряжений источника, а,,− векторы линейных напряжений источника, а также линейных напряжений приемника. Для построения вектора напряжения и векторов фазных напряжений приемника ,,используем их значения, полученные выше.

Рис. 4.9.

Связь между фазными и линейными векторами ,,и,,, определяем выражениями ,,.

Векторная диаграмма построена для активной несимметричной нагрузки фаз ().

При изменении величины фазных активных сопротивлений напряжение может изменяться в широких пределах. В соответствии с этим точкаN на диаграмме может занимать различные положения, а фазовые напряжения приемника могут отличаться друг от друга весьма существенно.

Рассмотрим, частный случай несимметричной нагрузки, когда . Поскольку, то и, получим,и. ТочкаN на диаграмме переместится в точку С, напряжение возрастет до фазного напряжения источника, а напряжения ,− до линейных напряжений.

Рис. 4.10.

При изменении фазных напряжений происходит изменение фазных токов и мощностей − «перекос фаз».

Если при несимметричной нагрузке нулевые точки источника и приемника соединить нулевым проводом, то поскольку сопротивление нулевого провода мало, (и), то фазные напряжения приемника получаются одинаковыми и сдвинутыми по фазе относительно друг друга на угол. Включение нулевого провода приводит к соответствующим изменениям векторной диаграммы электрической цепи. Так, если электрической цепи без нулевого провода соответствует векторная диаграмма, изображенная на рис.3.9. сплошной линией, то той же цепи при включении нулевого провода соответствует диаграмма, изображенная на том же рисунке пунктиром.

Вектор построен в соответствии с выражением. .

При наличии нулевого провода в схемах с несимметричной нагрузкой, так же как и в случае с симметричной нагрузкой остается в силе соотношение

.

На основании изложенного можно сделать вывод, что нулевой провод необходим для того, чтобы при несимметричной нагрузке выравнивать фазные напряжения приемника, т.е. получать во всех фазах приемника одинаковые напряжения, равные .

Фазные токи, углы сдвига фаз между фазовыми напряжениями и токами, а также фазные мощности при несимметричной нагрузке в цепи с нулевым проводом будут в общем случае различными. Они могут быть определены по следующим формулам: ,,.

Углы сдвига фаз между фазными токами и напряжениями зависят от величины и характера сопротивлений фаз приемника и равны

, ,.

Мощности для фазы «А» равны

Активная и реактивная мощности трехфазного приемника при соединении звездой ,.

Если кроме фазных токов требуется найти ток в нулевом проводе, то задачу следует решать в комплексной форме. При этом необходимо прежде всего выразить в комплексной форме то ,,

Ток в нулевом проводе можно определить также по векторной диаграмме, не прибегая к решению задачи в комплексной форме.

studfiles.net

27. Трехфазные цепи переменного тока. Соединение приемников звездой и треугольником. Основные определения

   Трехфазная  цепь  является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.

   Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.

     Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.

     Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.

       Соответственно                 

     На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы - последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу.       Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.

2. Соединение в звезду. Схема, определения

     Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.

Рис. 6.1

     Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N' называют нейтральным (нулевым) проводом.      Напряжения  между началами фаз  или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.        Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах - линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.

Iл = Iф.

ZN - сопротивление нейтрального провода.

     Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений

     (7.1)

     На рис. 6.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.

Рис. 6.2

       Из векторной диаграммы видно, что

       При симметричной системе ЭДС источника линейное напряжение больше фазного  в √3 раз.

Uл = √3 Uф

 

studfiles.net

4.3. Трехфазные цепи при соединении приемников звездой

Соединение звездой при симметричной нагрузке. При соединении приемников звездой концы фаз приемника соединены в общий узел N'. При этом концы всех фаз генератора соединены в общий узел N, а начала фаз — с нагрузкой — звездой сопротивлений.

Если узлы N и N' соединить проводом, называемым нейтральным, с сопротивлением ZN, то получим четырехпроводную цепь (рис. 4.7, а). Сопротивления проводов, связывающих источник с нагрузкой, можно учесть в сопротивлениях нагрузки Za,Zb,Zc.

Так как при соединении звездой фазы генератора соединены последовательно с фазами нагрузки, линейные токи одновременно являются и фазными токами как в фазах генератора, так и в фазах нагрузки:

(4.8)

За условные положительные направления линейных токов IА, IВ, IС принимают направления от источника к нагрузке, а за положительное направление тока в нейтральном проводе - от нагрузки к источнику.

Согласно первому закону Кирхгофа, ток в нейтральном проводе

(4.9)

При симметричной нагрузке поэтому токи в фазах приемника равны по значению и сдвинуты по фазе на один и тот же угол относительно соответствующих напряжений, т. е. φA = φB = φC = φ. Векторная диаграмма напряжений и токов для симметрич­ной нагрузки представлена на рис. 4.7, б. Из диаграммы видно, что ток в нейтральном проводе равен нулю (IN = 0), так как . Таким образом, если нагрузка равномерная, то необходимость в нейтраль­ном проводе отпадает. Трехфазная цепь без нейтрального провода яв­ляется трехпроводной.

Рассмотрим четырехпроводную цепь (рис. 4.7, а) более подробно. Найдем для этой цепи напряжение между нейтральными точками N и N', или смещение нейтрали, по методу двух узлов:

(4.10)

где - комплексы проводимостей фаз приемника;YN= 1/ZN -комплекс проводимости нейтрального провода. Так как при симметрич­ной нагрузке Ya = Yb = Yc, то (4.10) можно переписать в виде

(4.11)

При симметричной системе напряжений имеем

а значит, согласно (4.11), UNN =0. Так как ток в нейтральном проводе то при симметричной нагрузкеIN = 0. Следовательно, еще раз можно подчеркнуть, что при симметрич­ной нагрузке напряжение между нейтральными точками N и N' и ток в нейтральном проводе равны нулю.

Согласно второму закону Кирхгофа, для контуров (см. рис. 4.7, а) NAaN'N, NBbN'N, NCcN'N находим

(4.12) Так как при симметричной нагрузке UN’N =0, то из (4.12) следует, что

Итак, зная фазные напряжения и сопротивления нагрузки, находим токи в каждой фазе приемника:

(4-13)

Так как при симметричной нагрузке токи в фазах приемника равны, то достаточно определить ток только в одной из фаз трехфазной цепи.

Соединение звездой при несимметричной нагрузке. При несимметрич­ной нагрузке сопротивления приемника не одинаковы, т. е. Za ≠ Zb ≠ Zc. Для несимметричных нагрузок применяют четырехпроводные цепи, так как между точками N и N' появляется напряжение UN’N и напряжения на фазах нагрузки различны. При этом нарушается соотношение между фазными и линейными напряжениями причем на одних фазах нагрузки напряжение становится большим, а на других — меньшим, чем

Наличие нейтрального провода в цепи с несимметричной нагрузкой позволяет выравнивать напряжение на фазах приемника и поддержи­вать их неизменными, равными фазным напряжениям источника Uл /, т. е. нейтральный провод обеспечивает симметрию фазных напряжений приемника. Иначе говоря, при наличии нейтрального провода, когда ZN = 0, даже при несимметричной нагрузке фазные напря­жения приемника равны друг другу и соблюдается соотношение между фазными и линейными напряжениями .

Если нагрузка несимметрична (Za ≠ Zb ≠ Zc) и нейтральный провод имеет конечное сопротивление ZN, то напряжение UN’N между нейтраль­ными точками N' и N определяется по формуле (4.10), а напряжения на фазах нагрузки — по формулам (4.12). Тогда токи в схеме рис. 4.7, а

Если напряжения источника UA, UB, UC образуют симметричную систему, то при отсутствии нейтрального провода и при UN'N ≠ 0 напря­жения на фазе нагрузки Ua, Ub и Uc несимметричны, что видно из век­торной топографической диаграммы, приведенной на рис. 4.8. Особен­ностью этой диаграммы является то, что каждой точке электрической цепи А, В, С, N и N' соответствует определенная точка на диаграмме.

При этом расположение этих точек на диаграмме должно быть таким, чтобы отрезок, соединяющий любые точки на диаграмме, по длине и фазе определял напряжение между соответствующими точками цепи.

Напряжения на фазах нагрузки тем больше отличаются друг от друга, чем больше напряжение UN'N. Из выражения (4.10) и из топографи­ческой диаграммы (рис. 4.8) следует, что напряжение между нейтраль­ными точками UN'N будет изменяться при изменении нагрузки в любой фазе, при этом с изменением UN'N будет изменяться напряжение всех фаз приемника.

Чтобы напряжения на фазах нагрузки были одинаковыми, необхо­димо иметь UN'N= 0, что может быть получено двумя способами. Во-первых, выравниванием нагрузки в фазах приемника, когда YA = YB = YC = = Yф, а значит, согласно (4.10),

так как

Во-вторых, если имеется нейтральный провод с сопротивлением ZN’N = 0 (или YN’N = ∞ ), то напряжение UN'N, согласно (4.10), также при­нимает нулевое значение независимо от нагрузки фаз. Для этого случая построена векторная диаграмма (рис. 4.9). При обрыве нейтрального провода (ZN = ∞) и несимметричной на­грузке напряжение UN'N станет максималь­ным.

В фазах нагрузки могут возникнуть перенапряжения, поэтому в нейтральный провод плавкий предохранитель не ставят. Приемники электрической энергии мож­но подразделить на трехфазные и одно­фазные. К числу трехфазных относятся трехфазные электрические двигатели, имею­щие симметричные обмотки и обеспечиваю­щие равномерную нагрузку фаз. Такие электродвигатели включают в трехфаз­ную цепь звездой без нейтрального провода Однофазные приемники, к которым относятся электрические лампы, нагревательные приборы и ряд других приемников, всегда подключают к четырехпроводной цепи. Эти приемники подключаются на фазное напряжение, которое в раз меньше линейного напряжения сети.

Пример 4.1. К трехфазной линии напряжением Uл=380 В подключен несимметричный трехфазный приемник, соединенный звездой с нейтральным проводом (рис. а)). Активные и реактивные сопротивления фаз приемника соответственно равны: Ra = 19 Ом, Xa = 0 Ом, Rb= 8 Ом, Хb = 6 Ом, Rс = 24 Ом, Хc = 18 Ом. Сопротивлениями проводов можно пренебречь. Определить ток в фазах приемника, в линейных проводах и в нейтральном проводе.

а)

Рисунок к примеру 4.1.

Решение. Токи в линейных проводах и фазах приемника одинаковы и рассчитываются по закону Ома:

-

Фазное напряжение

Комплексные фазные напряжения:

Комплексные сопротивления фаз:

Токи в фазах приемника и проводах линии:

Ток в нейтральном проводе

Для построения топографической диаграммы напряжений выберем масштаб напряжений. В выбранном масштабе строим топографическую диаграмму напряжений. При построении векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на разные углы сдвига фаз: φа =0 — нагрузка чисто активная (Х=0), φb = 36°52' — нагрузка активно-индуктивная, φc = - 36052'— нагрузка активно-емкостная.

Действующее значение тока в нейтральном проводе равно 16,14 А, а его начальная фаза ψN= 2010. На диаграмме (рис. б) строим векто­ры токов

б)

Рисунок к примеру 4.1.

с учетом углов сдвига фаз. Вектор тока в нейтральном прово­де можно построить двумя способами: или как сумму векторов или непосредственно отложить вектор IN в соответствии с расчетными данными.

Пример 4.2. К трехпроводной трехфазной сети с линейным напряже­нием Uл=220 В подключен приемник, фазы которого соединены звез­дой, (рис.а)). Заданы сопротивления Rа = 10 Ом, Rb = 5 Ом, Хb = 9,66 Ом, Хс = 10 Ом. Определить токи в ветвях, построить совмещенную топографическую диаграмму напряжений и векторную диаграмму токов.

а)

Рисунок к примеру 4.2.

Решение. Фазные напряжения источника образуют симметричную систему

Комплексные сопротивления фаз приемника:

их комплексные подводимости

Смещение нейтрали

б)

Рисунок к примеру 4.2.

Фазные напряжения приемника:

Фазные токи и токи в линии:

Для построения векторных диаграмм выбираем масштабы напря­жения и тока. Строим симметричную топографическую диаграмму на­пряжений генератора ( рис. б)) и вектор смещения нейтрали UnN= 84e j205° В. Векторы, соединяющие точку n и точки а, b, с, соот­ветственно будут векторами фазных напряжений приемника Ua, Ub, Uc. Из точки n строим векторы токов Ia, Ib, Iс учетом сдвига фаз относи­тельно напряжений φa= 0°, φb= 60°, φc= — 90°.

Топографическая диаграмма напряжений показывает, что из-за смещения нейтрали симметрия фазных напряжений приемника наруша­ется: Ua= 206 В вместо Uф = 127 В; Uc = 145,6 В; Ub=75,5 В.

studfiles.net

3.3 Соединение звездой. Трехпроводная система трехфазного тока.

В четырехпроводной системе трехфазного тока, включенной по схеме звезда, при симметричной нагрузке ток в нейтральном проводе равен нулю. Следовательно, в этом случае от нейтрального провода можно отказаться, и четырехпроводная система при этом превращается в трехпроводную систему трехфазного тока (рис. 3.7.)

Рис. 3.7 Трехпроводная трехфазная система «звезда».

Топографическая векторная диаграмма, токов и напряжений в трехпроводной системе «звезда» при симметричной нагрузке аналогична соответствующей диаграмме четырехпроводной системы (рис. 3.6.а).

При несимметричной нагрузке в трехфазной системе действующие значения токов IА, IВ, IC не будут равны между собой, однако, в соответствии с первым законом Кирхгофа, их геометрическая сумма должна быть равна нулю. Поэтому токи в этом случае не будут представлять собой симметричную трехфазную систему. Следовательно, изменятся и фазные напряжения на нагрузке, т.е. симметричные фазные напряжения станут несимметричными, их действующие значения не будут равны между собой, а сдвиги фаз между ними будут отличаться от 1200. Между нулевыми точками генератора N и нагрузки n появится напряжение UNn, называемое напряжением смещения.

Топографическая векторная диаграмма трехпроводной системы «звезда» при несимметричной активной нагрузке представлена ни рис. 3.8.

Рис.3.8. Топографическая векторная диаграмма трехпроводной трехфазной системы «звезда» при несимметричной активной нагрузке

Анализ векторной диаграммы позволяет сделать следующие выводы:

Напряжения между линейными проводами остаются равными по величине (UAB= UBC= UCA) и взаимно сдвинутыми по фазе на 120о как при симметричной, так и при несимметричной нагрузке фаз. Фазные же напряжения в трехпроводной сети одинаковы по величине только в случае симметричной нагрузки фаз. При нарушении симметричности нагрузки напряжения между линейными проводами и нулевой точкой, т.е. фазные напряжения потребителей UА, UВ и UCбудут неодинаковы. Поэтому соотношение UЛ=Uф в трехпроводной сети справедливо только при симметричной нагрузке фаз.

Электрические сети выполняются трехпроводными только для питания таких потребителей, которые обеспечивают симметричную нагрузку фаз (например, электрические двигатели).

3.4. Соединение по схеме «треугольник».

Если конец первой фазы трехфазного генератора соединить с началом второй, конец второй фазы с началом третьей, конец третьей фазы с началом первой, то получится соединение треугольником. По такому принципу могут быть соединены и сопротивления нагрузки. Одноименные вершины фаз генератора и фаз нагрузки соединяются между собой линейными проводами (рис. 3.9)

По сопротивлениям нагрузки проходят фазные токи IAB, IBC и IСА, а по линейным проводам линейные IA, IB и IC. Принятые положительные направления фазных и линейных токов обозначены стрелками. Напряжения, приложенные к сопротивлениям нагрузки ZAB, ZBC и ZСА называются фазными напряжениями.

Таким образом, при соединении потребителей трехфазного тока треугольником фазные напряжения равны линейным Uф= UЛ

Рис.3.9 Система трехфазного тока при соединении треугольником.

По первому закону Кирхгофа для узловых точек А, В, и С имеем

iA = iAB – iCA

iB = iBC – iAB (3.4)

iC= iCA – iBC

В действующих значениях токов система (3.4) справедлива в векторной форме:

A = AB – CA

B = BC – AB (3.5)

C= CA – BC

Из системы уравнений (3.5) следует:

1. Каждый линейный ток в трехфазной цепи при соединении треугольником равен геометрической разности двух прилегающих к узловой точке фазных токов;

2. При любых значениях фазных токов геометрическая сумма линейных токов равна нулю, как при симметричной, так и при несимметричной нагрузке.

На основании системы уравнений (3.5) построим векторную диаграмму фазных и линейных токов при соединении треугольником при симметричной нагрузке (рис. 3.10).

Рис. 3.10. Векторная диаграмма трехпроводной системы «треугольник» при симметричной нагрузке.

Из треугольника OEМ найдем связь между фазными и линейными токами, применив рассуждения, аналогичные рассмотренным для напряжений при соединении звездой (см. раздел 3.2), получаем

IЛ = 2 Iф cos300 =.

Таким образом, при симметричной нагрузке системы, соединенной в треугольник, линейные токи больше фазных в раз, а линейные напряжения равны фазным.

Соединение треугольником применяется только для питания потребителей, обеспечивающих симметричную нагрузку.

studfiles.net

Соединение фаз генератора и приемника звездой

При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Za, Zb, Zc) также соединяют в одну точку n. Такое соединение называется соединение звезда.

Рис. 3.6

Провода A−a, B−b и C−c, соединяющие начала фаз генератора и приемника, называются линейными, провод N−n, соединяющий точку N генератора с точкой n приемника, – нейтральным.

Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной.

В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (UA, UB, UC у источника; Ua, Ub, Uc у приемника). Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (UA=Ua, UB=Ub, UC=Uc). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз.

Линейное напряжение (UЛ) – напряжение между линейными проводами или между одноименными выводами разных фаз (UAB, UBC, UCA). Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).

По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи:

При соединении в звезду фазные и линейные токи равны

(3.5)

IФ=IЛ.

Ток, протекающий в нейтральном проводе, обозначают IN.

По первому закону Кирхгофа для нейтральной точки n (N) имеем в комплексной форме

(3.6)

İN=İA+İB+İC.

Рис. 3.7

В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа.

(3.7)

ÚAB=ÚA−ÚB; ÚBC=ÚB−ÚC; ÚCA=ÚC−ÚA.

Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: UAB, UBC,UCA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение UЛ), и опережают, соответственно, векторы фазных напряжений UA, UB, UC, (UФ) на угол 30°.

Действующие значения линейных напряжений можно определить графи-чески по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений:

UЛ=2UФcos30°

или

(3.8)

UЛ=UФ.

Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями:

UЛ=660В;UФ=380В; UЛ=380В;UФ=220В; UЛ=220В;UФ=127В.

Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи.

Классификация приемников в трехфазной цепи

Приемники, включаемые в трехфазную цепь, могут быть либо однофазными, либо трехфазными. К однофазным приемникам относятся электрические лампы накаливания и другие осветительные приборы, различные бытовые приборы, однофазные двигатели и т.д. К трехфазным приемникам относятся трехфазные асинхронные двигатели и индукционные печи. Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:

(3.9)

Za = Zb = Zc = Zejφ.

Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.

Четырехпроводная цепь

Для расчета трехфазной цепи применимы все методы, используемые для расчета линейных цепей. Обычно сопротивления проводов и внутреннее сопротивление генератора меньше сопротивлений приемников, поэтому для упрощения расчетов таких цепей (если не требуется большая точность) сопротивления проводов можно не учитывать (ZЛ = 0, ZN = 0). Тогда фазные напряжения приемника Ua, Ub и Ucбудут равны соответственно фазным напряжениям источника электрической энергии(генератора или вторичной обмотки трансформатора), т.е. Ua = UA; Ub = UB; Uc = UC. Если полные комплексные сопротивления фаз приемника равны Za = Zb = Zc, то токи в каждой фазе можно определить по формулам

(3.10)

İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.

В соответствии с первым законом Кирхгофа ток в нейтральном проводе

(3.11)

İN = İa + İb + İc = İA + İB + İC.

Симметричная нагрузка приемника

При симметричной системе напряжений и симметричной нагрузке, когда Za = Zb = Zc, т.е. когда Ra = Rb = Rc = Rф и Xa = Xb = Xc = Xф, фазные токи равны по значению и углы сдвига фаз одинаковы

(3.12)

Ia = Ib = Ic = Iф = Uф / Zф,

(3.13)

φa = φb = φc = φ = arctg (Xф/Rф).

Построив векторную диаграмму токов для симметричного приемника (рис. 3.8), легко установить, что геометрическая сумма трех векторов тока равна нулю: İa + İb + İc = 0. Следовательно, в случае симметричной нагрузки ток в нейтральном проводе IN = 0, поэтому необходимость в нейтральном проводе отпадает.

Рис. 3.8

Несимметричная нагрузка приемника

При симметричной системе напряжений и несимметричной нагрузке, когда Za ≠ Zb ≠ Zc и φa ≠ φb ≠ φc токи в фазах потребителя различны и определяются по закону Ома

İa = Úa / Za; İb = Úb / Zb; İc = Úc / Zc.

Ток в нейтральном проводе İN равен геометрической сумме фазных токов

İN = İa + İb + İc.

Напряжения будут Ua = UA; Ub = UB; Uc = UC, UФ = UЛ / , благодаря нейтральному проводу при ZN = 0.

Следовательно, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.

Поэтому в четырехпроводную сеть включают однофазные несимметричные нагрузки, например, электрические лампы накаливания. Режим работы каждой фазы нагрузки, находящейся под неизменным фазным напряжением генератора, не будет зависеть от режима работы других фаз.

Векторная диаграмма при несимметричной нагрузке приведена на рис. 3.9

Рис. 3.9

Трехпроводная электрическая цепь

Схема соединения источника и приемника звездой без нейтрального провода приведена на рис. 3.10.

Рис. 3.10

При симметричной нагрузке, когда Za = Zb = Zc = Zφ, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, UnN = 0.

Соотношение между фазными и линейными напряжениями приемника также равно , т.е. UФ = UЛ / , а токи в фазах определяются по тем же формулам (3.12, 3.13), что и для четырехпроводной цепи. В случае симметричного приемника достаточно определить ток только в одной из фаз. Сдвиг фаз между током и соответствующим напряжением φ = arctg (X / R).

При несимметричной нагрузке Za ≠ Zb ≠ Zc между нейтральными точками приемника и источника электроэнергии возникает напряжение смещения нейтрали UnN.

Для определения напряжения смещения нейтрали можно воспользоваться формулой межузлового напряжения, так как схема рис 3.10 представляет собой схему с двумя узлами,

(3.14)

,

где: Ya = 1 / Za; Yb = 1 / Zb; Yc = 1 / Zc – комплексы проводимостей фаз нагрузки.

Очевидно, что теперь напряжения на фазах приемника будут отличаться друг от друга. Из второго закона Кирхгофа следует, что

(3.15)

Úa = ÚA - ÚnN; Úb = ÚB - ÚnN; Úc = ÚC - ÚnN.

Зная фазные напряжения приемника, можно определить фазные токи:

(3.16)

İa = Úa / Za = Ya Úa; İb = Úb / Zb = Yb Úb; İc = Úc / Zc = Yc Úc.

Векторы фазных напряжений можно определить графически, построив векторную (топографическую) диаграмму фазных напряжений источника питания и UnN (рис. 3.11).

При изменении величины (или характера) фазных сопротивлений напряжение смещений нейтрали UnN может изменяться в широких пределах. При этом нейтральная точка приемника n на диаграмме может занимать разные положения, а фазные напряжения приемника Úa, Úb и Úc могут отличаться друг от друга весьма существенно.

Таким образом, при симметричной нагрузке нейтральный провод можно удалить и это не повлияет на фазные напряжения приемника. При несимметричной нагрузке и отсутствии нейтрального провода фазные напряжения нагрузки уже не связаны жестко с фазными напряжениями генератора, так как на нагрузку воздействуют только линейные напряжения генератора. Несимметричная нагрузка в таких условиях вызывает несимметрию ее фазных напряжений Úa, Úb, Úc и смещение ее нейтральной точки n из центра треугольника напряжений (смещение нейтрали).

Рис. 3.11

Направление смещения нейтрали зависит от последовательности фаз системы и характера нагрузки.

Поэтому нейтральный провод необходим для того, чтобы:

• выравнивать фазные напряжения приемника при несимметричной нагрузке;

• подключать к трехфазной цепи однофазные приемники с номинальным напряжением в раз меньше номинального линейного напряжения сети.

Следует иметь в виду, что в цепь нейтрального провода нельзя ставить предохранитель, так как перегорание предохранителя приведет к разрыву нейтрального провода и появлению значительных перенапряжений на фазах нагрузки.

studfiles.net

Соединение в звезду. Схема, определения

Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.

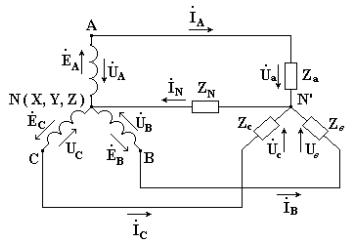
Рис. 7.1

Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N' называют нейтральным (нулевым) проводом. Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями. Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах - линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.

Iл = Iф.

ZN - сопротивление нейтрального провода.

Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений

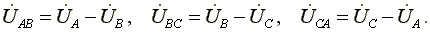(7.1)

На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.

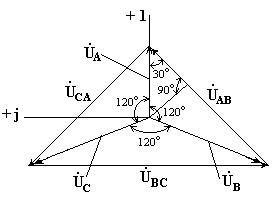
Рис. 7.2

Из векторной диаграммы видно, что

При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.

Uл = √3 Uф

Частные случаи.

1. Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению ZA = ZB = ZC = R.

В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.

2. Нагрузка несимметричная, RA < RB = RC, но сопротивление нейтрального провода равно нулю: ZN = 0.

Фазные напряжения нагрузки и генератора одинаковы

 

 

 

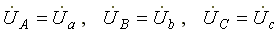
Рис. 7.6

Фазные токи определяются по формулам

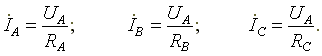
Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.

На рис. 7.6 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.

3. Нагрузка несимметричная, RA < RB = RC, нейтральный провод отсутствует,

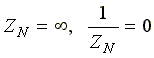
В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:

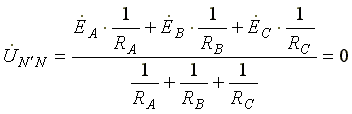
Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора. Из-за напряжения смещения нейтрали фазные напряжения нагрузки становятся неодинаковыми. Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.

 

7.3. Соединение в треугольник. Схема, определения

Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке. На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.

Uл = Uф

IA, IB, IC - линейные токи;

Iab, Ibc, Ica- фазные токи.

Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.

 

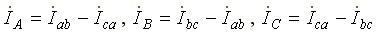
Рис. 7.3

Линейный ток равен геометрической разности соответствующих фазных токов. На рис. 7.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.

Рис. 7.4

Из векторной диаграммы видно, что

,

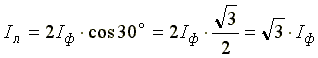Iл = √3 Iфпри симметричной нагрузке.

Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме "звезда". Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.

Похожие статьи:

poznayka.org

---

• 
  Вольер для двух собак своими руками схемы и чертежи
• 
  Схемы элементы
• 
  Обозначение на схеме коммутатора
• 
  Определить эквивалентную емкость батареи конденсаторов соединенных по схеме
• 
  Схемы включения реле
• 
  Схемы теплых полов
• 
  Опс на схеме обозначение
• 
  Разработка схем электрических принципиальных
• 
  Как выбрать флюс для пайки микросхем
• 
  Терморезистор на схеме
• 
  Треугольник и звезда схемы