Переменный электрический ток. Закон Ома. Переме́нный ток, AC (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению. Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону. В устройствах-потребителях постоянного тока переменный ток часто преобразуется выпрямителями для получения постоянного тока. Закон ома для переменного тока в общем случае имеет такой же вид, как и для постоянного. То есть при увеличении напряжения в цепи ток также в ней будет увеличиваться. Отличием же является то, что в цепи переменного тока сопротивление ему оказывают такие элементы как катушка индуктивности и емкость. Учитывая этот факт, запишем закон ома для переменного тока. Формула 1 — закон ома для переменного тока где z это полное сопротивление цепи. Формула 2 — полное сопротивление цепи В общем случае полное сопротивление цепи переменного тока будет состоять из активного емкостного и индуктивного сопротивления. Проще говоря, ток в цепи переменного тока, зависит не только от активного омического сопротивление, но и от величины емкости и индуктивности. Рисунок 1 — цепь, содержащая омическое индуктивное и емкостное сопротивление Если, например, в цепь постоянного тока включить конденсатор то тока в цепи не будет, так как конденсатор на постоянном токе является разрывом цепи. Если же в цепи постоянного тока появится индуктивность, то ток не изменится. Строго говоря, изменится, так как катушка будет обладать омическим сопротивлением. Но изменение будет ничтожным. Если же конденсатор и катушку включить в цепи переменного тока, то они будут оказывать сопротивление току пропорционально величине ёмкости и индуктивности соответственно. Кроме этого в цепи буде наблюдаться сдвиг фаз между напряжением и током. В общем случае ток в конденсаторе опережает напряжение на 90 градусов. В индуктивности же отстает на 90 градусов. Емкостное сопротивление зависит от величины емкости и частоты переменного тока. Эта зависимость обратно пропорциональна, то есть с увеличением частоты и ёмкости сопротивление будет уменьшаться. Формула 3 — емкостное сопротивление Индуктивное сопротивление прямо пропорционально частоте и индуктивности. Чем больше индуктивность и частота, тем больше сопротивление переменному току будет оказывать данная катушка. studfiles.net Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой щ и амплитудой Um, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im. Установим связь между амплитудами колебаний силы тока и напряжения В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения: Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону: Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на р/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на р/2. Поэтому уравнение (1) можно записать так: где URm, UCm и ULm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке. Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм. При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения URm, совпадает по направлению с вектором, изображающим амплитуду силы тока ImКолебания напряжения на конденсаторе отстают по фазе на р/2 от колебаний силы тока, поэтому вектор UCmотстает от вектора Im на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на р/2, поэтому вектор ULmопережает вектор Im на угол 90° (рис. 9). На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов Rm, Cm,Lmвращающихся с одинаковой угловой скоростью щ против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений uR, uC, и uLна отдельных элементах цепи, т.е. сумме проекций векторов URm, UCm и ULmна горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов: Из рисунка 9 видно, что амплитуда напряжений на всей цепи равна: Или Отсюда Введя обозначение для полного сопротивления цепи переменного тока: выразим связь между амплитудными значениями силы тока и напряжения в цепи переменного тока следующим образом: Это выражение называют законом Ома для цепи переменного тока. Из векторной диаграммы, приведенной на рисунке 9, видно, что фаза колебаний полного напряжения равна щ∙t + ц. Поэтому мгновенное значение полного напряжения определяется формулой: Начальную фазу ц можно найти из векторной диаграммы: Величина cos ц играет важную роль при вычислении мощности в электрической цепи переменного тока. Мощность в цепи переменного тока Мощность в цепи постоянного тока определяется произведением напряжения на силу тока: Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой: Пусть напряжение на концах цепи меняется по гармоническому закону: При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период. Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов: Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени: При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно: Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I2∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим: Действующим значением силы тока называют величину, в √2 раз меньшую ее амплитудного значения: Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока. Аналогично можно доказать, что действующее значение переменного напряжения в √2 раз меньше его амплитудного значения: Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать: Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз цc между напряжением и током. Множитель cos цc в формуле называется коэффициентом мощности. В случае, когда цc = ± р/2, энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при цc = – р/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть. Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит. При проектировании цепей переменного тока нужно добиваться, чтобы cos цc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов. Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos цc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos цc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos цc < 0,85. studfiles.net Определение 1 Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом: Рисунок 1. Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим: где $U$ -- напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно: где коэффициент $R$ -- называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла. Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$. Рисунок 2. Мы можем использовать следующие соотношения: Если $I(t)$ определена уравнением (1), то заряд выражен как: где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно: Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $\frac{\pi }{2}.$ Амплитуда напряжения на емкости равна: Величину $X_C=\frac{1}{\omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=\infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока. Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$. Рисунок 3. Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид: По условию $R=0. \mathcal E$ самоиндукции можно выразить как: Из выражений (8), (9) следует, что: Амплитуда напряжения в данном случае равна: где $X_L-\ $индуктивное сопротивление (кажущееся сопротивление индуктивности). Определение 2 Выражение вида: где называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям. Пример 1 Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $\nu$. Решение: Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова. Амплитудное значение силы тока выражается «законом Ома для переменного тока»: оно связано с действующим значением силы тока как: В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу: Подставим в формулу (1.2) формулы (1.1) и (1.3), получим: где $\omega =2\pi \nu .$ Ответ: $I=\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$ Пример 2 Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$). Решение: Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой: Напряжение на активном сопротивлении ($U_R$) равно: Напряжение на конденсаторе ($U_C$) определяется как: Ответ: $U_L=2\pi \nu L\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},\ U_R=\frac{UR}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}},U_C=\frac{1}{C2\pi \nu }\frac{U}{\sqrt{R^2+{\left(2\pi \nu L-\frac{1}{2\pi \nu C}\right)}^2}}.$ spravochnick.ru В § 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности: Эти соотношения во виду напоминают закон Ома для участка цепи неизменного тока, но только сейчас в их входят не значения неизменных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений. Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из частей R, L и C. Физические величины R, и ωL именуются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки. При протекании переменного тока по участку цепи электрическое поле совершает работу, и в цепи выделяется джоулево тепло. Моментальная мощность в цепи переменного тока равна произведению моментальных значений тока и напряжения: p = J · u. Практический энтузиазм представляет среднее за период переменного тока значение мощности Тут I0 и U0 – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг меж током и напряжением. Черта значит символ усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0: Для того, чтоб это выражение по виду совпадало с формулой для мощности неизменного тока, вводятся понятия действующих либо действенных значений силы тока и напряжения: Средняя мощность переменного тока на участке цепи, содержащем резистор, равна Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг меж током и напряжением Потому Аналогично можно показать, что PL = 0. Таким макаром, мощность в цепи переменного тока выделяется лишь на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю. Разглядим сейчас электронную цепь, состоящую из поочередно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех поочередно соединенных участках цепи протекает один и тот же ток. Меж напряжением наружного источника e(t) и током J(t) появляется фазовый сдвиг на некий угол φ. Потому можно записать Такая запись моментальных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 5.3.2). Средняя мощность, развиваемая источником переменного тока, равна Как видно из векторной диаграммы, UR = 0 · cos φ, потому Как следует, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает изготовленный ранее вывод. В § 2.3 было выведено соотношение меж амплитудами тока I0 и напряжения 0 для поочередной RLC-цепи: Величину именуют полным сопротивлением цепи переменного тока. Формулу, выражающую связь меж амплитудными значениями тока и напряжения в цепи, можно записать в виде Это соотношение именуют законом Ома для цепи переменного тока. Формулы (*), приведенные сначала этого параграфа, выражают личные случаи закона Ома (**). Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи в почти всех случаях комфортно использовать приятный способ векторных диаграмм. Разглядим в качестве примера параллельный RLC-контур, присоединенный к наружному источнику переменного тока (рис. 5.4.1). При построении векторной диаграммы следует учитывать, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению наружного источника. Токи, текущие в различных ветвях цепи, отличаются не только лишь по значениям амплитуд, да и по фазовым сдвигам относительно приложенного напряжения. Потому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей неизменного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 5.4.2. Из диаграммы следует: Потому полное сопротивление параллельного RLC-контура выражается соотношением При параллельном резонансе (ω2 = 1 / LC) полное сопротивление цепи воспринимает наибольшее значение, равное активному сопротивлению резистора: Фазовый сдвиг φ меж током и напряжением при параллельном резонансе равен нулю. homework.net.ua В 2.3 были выведены соотношения, связывающие амплитуды переменных токов и напряжений на резисторе, конденсаторе и катушке индуктивности: Эти соотношения во виду напоминают закон Ома для участка цепи постоянного тока, но только теперь в них входят не значения постоянных токов и напряжений на участке цепи, а амплитудные значения переменных токов и напряжений. Соотношения (*) выражают закон Ома для участка цепи переменного тока, содержащего один из элементов R, L и C. Физические величины R, При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J · u. Практический интерес представляет среднее за период переменного тока значение мощности Здесь I0 и U0 – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0: Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения: Средняя мощность переменного тока на участке цепи, содержащем резистор, равна Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением Аналогично можно показать, что PL = 0. Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю. Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать J (t) = I0 cos ωt; e (t) = Такая запись мгновенных значений тока и напряжения соответствует построениям на векторной диаграмме (рис. 2.3.2). Средняя мощность, развиваемая источником переменного тока, равна Как видно из векторной диаграммы, UR = В 2.3 было выведено соотношение между амплитудами тока I0 и напряжения Величину называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде ZI0 = (**) Это соотношение называют законом Ома для цепи переменного тока. Формулы (*), приведенные в начале этого параграфа, выражают частные случаи закона Ома (**). Понятие полного сопротивления играет важную роль при расчетах цепей переменного тока. Для определения полного сопротивления цепи во многих случаях удобно использовать наглядный метод векторных диаграмм. Рассмотрим в качестве примера параллельный RLC-контур, подключенный к внешнему источнику переменного тока (рис. 2.4.1). Рисунок 2.4.1. Параллельный RLC-контур При построении векторной диаграммы следует учесть, что при параллельном соединении напряжение на всех элементах R, C и L одно и то же и равно напряжению внешнего источника. Токи, текущие в разных ветвях цепи, отличаются не только по значениям амплитуд, но и по фазовым сдвигам относительно приложенного напряжения. Поэтому полное сопротивление цепи нельзя вычислить по законам параллельного соединения цепей постоянного тока. Векторная диаграмма для параллельного RLC-контура изображена на рис. 2.4.2. Рисунок 2.4.2. Векторная диаграмма для параллельного RLC-контура Из диаграммы следует: Поэтому полное сопротивление параллельного RLC-контура выражается соотношением При параллельном резонансе (ω2 = 1 / LC) полное сопротивление цепи принимает максимальное значение, равное активному сопротивлению резистора: Фазовый сдвиг φ между током и напряжением при параллельном резонансе равен нулю. questions-physics.ru После того как в 1831 г. Фарадеем было открыто явление электромагнитной индукции, электротехника начала свой стремительный марш из лабораторий ученых в промышленность. Появляются первые генераторы постоянного, а затем и переменного тока. Важным преимуществом последних явилось то, что переменный ток можно было передавать потребителю с меньшими потерями. Цепи переменного электрического тока имеют ряд особенностей, и, естественно, предполагали, что математический расчет их должен быть не таким, как расчет цепей постоянного тока. Однако Гельмгольц в работе «О процессе протекания индукционных токов...» показал, что закон Ома можно применять и для расчета электрических цепей переменного тока. Используя закон Ома для участка цепи, можно рассчитать сопротивление участков, содержащих различные элементы — индуктивность и емкость. Рассмотрим простейший способ расчета электрических цепей переменного тока. Пусть генератор переменного тока создает в цепи ЭДС где Если значения емкости С и индуктивности L исследуемого участка цепи переменного тока пренебрежимо малы, то, используя закон Ома, найдем напряжение на участке цепи, сопротивление которого r : где Если индуктивность исследуемого участка пренебрежимо мала (L ≈ 0), а значением емкости пренебречь нельзя, то результаты расчета будут несколько иными. Зная, что мгновенное значение силы тока определяется выражением можно найти количество электричества, протекающее за время t через поперечное сечение исследуемого участка: Подставляя в это выражение значение переменного тока, получим: или после интегрирования: Постоянная интегрирования имеет смысл заряда, которым обладает конденсатор до включения его в цепь. Если в цепь включают незаряженный конденсатор, то можно считать С0 = 0 и тогда Так как емкость конденсатора выражается формулой то напряжение на концах участка цепи, содержащего емкость, определим по формуле: Сравнивая формулы для силы тока и напряжения, замечаем, что на участке цепи, содержащем емкость, значение напряжения отстает от значения силы тока по фазе на π/2, то есть сила тока достигает максимума в тот момент, когда напряжение на исследуемом участке обращается в нуль. Амплитудное значение напряжения для указанного случая определяется выражением Снова используя закон Ома для участка цепи, получим формулу, позволяющую вычислить емкостное сопротивление участка: Приведем расчет участка цепи переменного тока, содержащего индуктивность; значение емкости этого участка учитывать не будем вследствие его малости. Зная, что при изменении тока в катушке индуктивности в ней возникает ЭДС самоиндукции, запишем для этого случая закон Ома: Пренебрегая активным сопротивлением исследуемого участка (r = 0) и учитывая, что ЭДС самоиндукции определяется по закону получим: Для тока, изменяющегося синусоидально, найдем: или Сравнивая выражения для тока и напряжения, видим, что напряжение на концах участка цепи, содержащего индуктивность, опережает ток в нем по фазе на π/2. Амплитудное значение напряжения для этого случая определим по формуле: Используя закон Ома, найдем формулу для расчета индуктивного сопротивления участка цепи: Расчет участка цепи переменного тока, содержащего активное сопротивление, индуктивность и емкость, проведенный с привлечением метода векторных диаграмм, дает для амплитудного значения напряжения на концах этого участка следующее выражение: Сопротивление этого участка определяется формулой где R — полное сопротивление исследуемого участка цепи, r — активное сопротивление этого участка, Максимального значения переменный ток достигает при условии т. е. при значении частоты переменного тока что соответствует периоду колебаний Если частота переменного тока, вырабатываемая генератором, достигнет частоты собственных колебаний тока в некотором контуре, подключенном к генератору, то в контуре будет наблюдаться резкое возрастание амплитуды колебаний, т. е. резонанс. Приведенные рассуждения показывают плодотворность приложения закона Ома к расчету цепей переменного тока. Использование закона Ома для цепей переменного тока дает возможность вскрыть механизм электрического сопротивления основных элементов цепи — емкости и индуктивности. Это имеет большое значение в практике, так как неправильный расчет цепи может привести к резонансу силы тока или напряжения и вызвать повреждение приборов, включенных в эту цепь. Расчеты цепей переменного тока позволяют добиться такого изменения индуктивности и емкости цепи, чтобы разность фаз между силой тока и напряжением была наименьшей. Это влечет за собой повышение мощности переменного тока. С таким же успехом применяют закон Ома для расчета цепей, питающихся от генератора, ЭДС которого изменяется по какому-либо другому периодическому закону. vestishki.ru Рассмотрим следующую цепь. картинка К источнику переменного напряжения последовательно подключены катушка индуктивности, активное сопротивление и конденсатор. В источнике тока напряжение поддерживается согласно гармоническому закону. u = Um*sin(ω*t). При отдельном подключении каждого из этих элементов амплитуды силы тока определялись по следующим формулам: Im = Um/R, Im = Um/(ω*L) = Um/ XL, Im = Um*C*ω = Um/Xc. Амплитуды напряжений на этих элементах будут вычисляться по формулам: Um = Im*R, Um = Im/(C*ω), Um = Im* ω*L. В цепи постоянного тока падение напряжения на всей цепи будет равняться сумме падений напряжений на каждом её участке. Если же попробовать сделать так же и здесь, то получим разные значения. Тут дело в том, что напряжения на разных участках цепи сдвинуты по фазе относительно друг друга. Поэтому чтобы их складывать, необходимо учитывать этот факт. Самый простой способ это сделать - это использовать векторные диаграммы. Сила тока одинакова во все цепи, следовательно, построение начнем с неё. Нарисуем её в виде вектора направленного вверх.Напряжение на активном сопротивлении совпадает по фазе с силой тока, следовательно, его рисуем сонаправленным с вектором силы тока. Модуль вектора равен Um = Im*R. Колебание напряжения на катушке опережает колебания силы тока на pi/2. Вектор этого напряжения поворачиваем относительно вектора силы тока, на указанный угол. Модуль вектора равен Um = Im* ω*L. Колебание напряжения на конденсаторе отстает по фазе на pi/2 от колебания силы тока. Этот вектор рисуем на указанный угол. Если в прошлый раз направление положительного угла взяли против часовой стрелки, то значит этот вектор необходимо нарисовать вправо. Модуль вектора равен Um = Im/(C*ω). Получится следующий рисунок. картинка Теперь эти вектора надо сложить. Складывая эти вектора, получим результирующий вектор Um картинка По теореме Пифагора вектор Um будет равен: Um = Im*√(R^2 +(ω*L – 1/(C*ω))^2). Отсюда находим выражение для амплитуды колебания силы тока: Im = Um/√(R^2 +(ω*L – 1/(C*ω))^2). Это выражение будет описывать закон Ома для цепи с переменным током. Величина √(R^2 +(ω*L – 1/(C*ω))^2) = Z будет называться полным сопротивлением цепи. Все неприличные комментарии будут удаляться. www.nado5.ru5. Закон Ома для электрической цепи переменного тока. Закон ома для цепи переменного тока
Переменный электрический ток. Закон Ома
5. Закон Ома для электрической цепи переменного тока
Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока
Активное сопротивление
Ёмкостное сопротивление
Индуктивное сопротивление
Закон Ома для цепей переменного тока
Закон Ома для цепи переменного тока. Мощность. – HomeWork.net.ua
(*) J(t) = I0 cos ωt; e(t) = 0 cos (ωt + φ). ZI0 = 0. (**) 1 Набросок 5.4.1. Параллельный RLC-контур. 2 Набросок 5.4.2. Векторная диаграмма для параллельного RLC-контура. Закон Ома для цепи переменного тока. Мощность
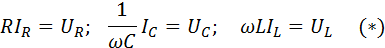
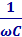 и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
и ωL называются активным сопротивлением резистора, емкостным сопротивлением конденсатора и индуктивным сопротивлением катушки.
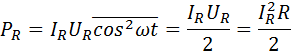
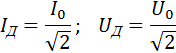
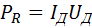
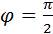 . Поэтому
. Поэтому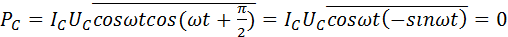
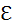 0 cos (ωt + φ).
0 cos (ωt + φ).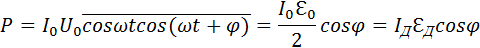
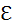 0 · cos φ, поэтому
0 · cos φ, поэтому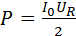 . Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.
. Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе, что подтверждает сделанный ранее вывод.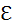 0 для последовательной RLC-цепи:
0 для последовательной RLC-цепи: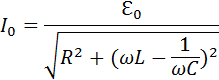
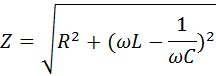
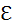 0.
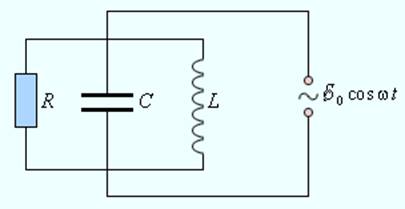
0.
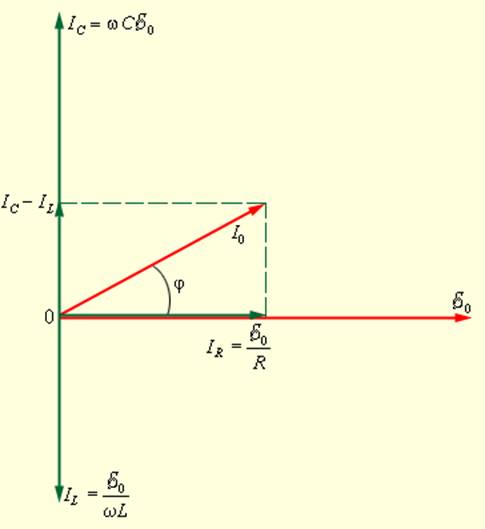
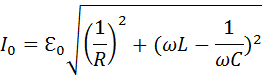
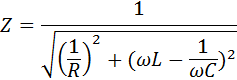
Закон Ома для переменного тока
, которая изменяется по синусоидальному закону:
— амплитудное значение ЭДС; ω — циклическая частота. В этом случае и сила тока, возбуждаемого во внешней части цепи, будет изменяться по такому же закону:
— амплитудное значение напряжения. Из полученного следует, что если на некотором участке цепи практически отсутствуют индуктивность и емкость, то переменный ток и напряжение на концах этого участка совпадают по фазе.
— его реактивное сопротивление.
Закон Ома для переменного тока: примеры выражений и формулы
Нужна помощь в учебе?
Предыдущая тема: Индуктивное сопротивление: ЭДС самоиндукции и формулы Следующая тема:   Открытие электромагнитной индукции: магнитный поток
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''











Поделиться с друзьями: