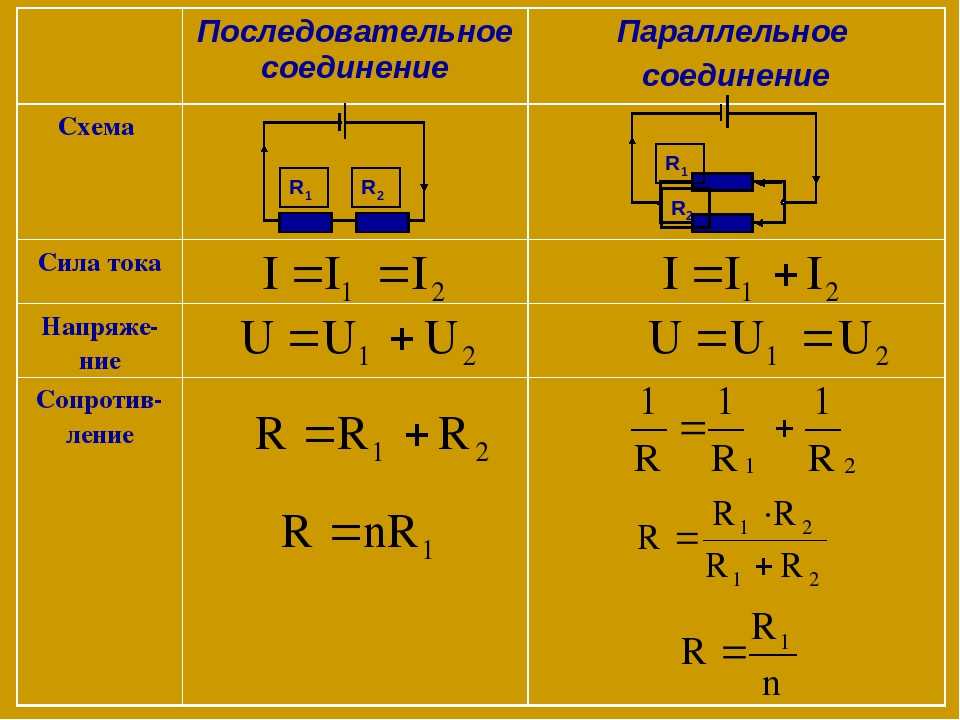
Содержание
Последовательное соединение резисторов. Схема соединения и примеры расчета
Главная » Справочник » Последовательное соединение резисторов. Схема соединения и примеры расчета
Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.
Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:
R = R1 + R2 + R3
То есть, в нашем случае общее сопротивление цепи будет равно:
R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм
Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.
Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.
Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).
Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Подробнее
Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:
Используя закон Ома для участка цепи, напряжение на отдельных резисторов может быть вычислена следующим образом:
В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.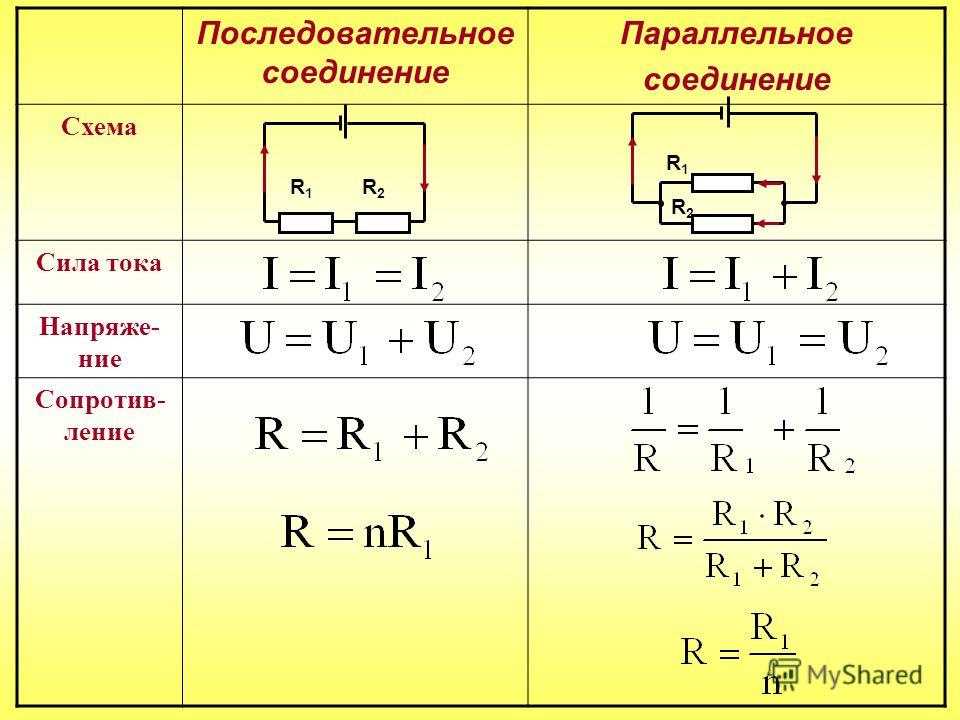
В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
Необходимо рассчитать падение напряжения на выводах «А» и «В»:
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
Подробнее
Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления
Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов.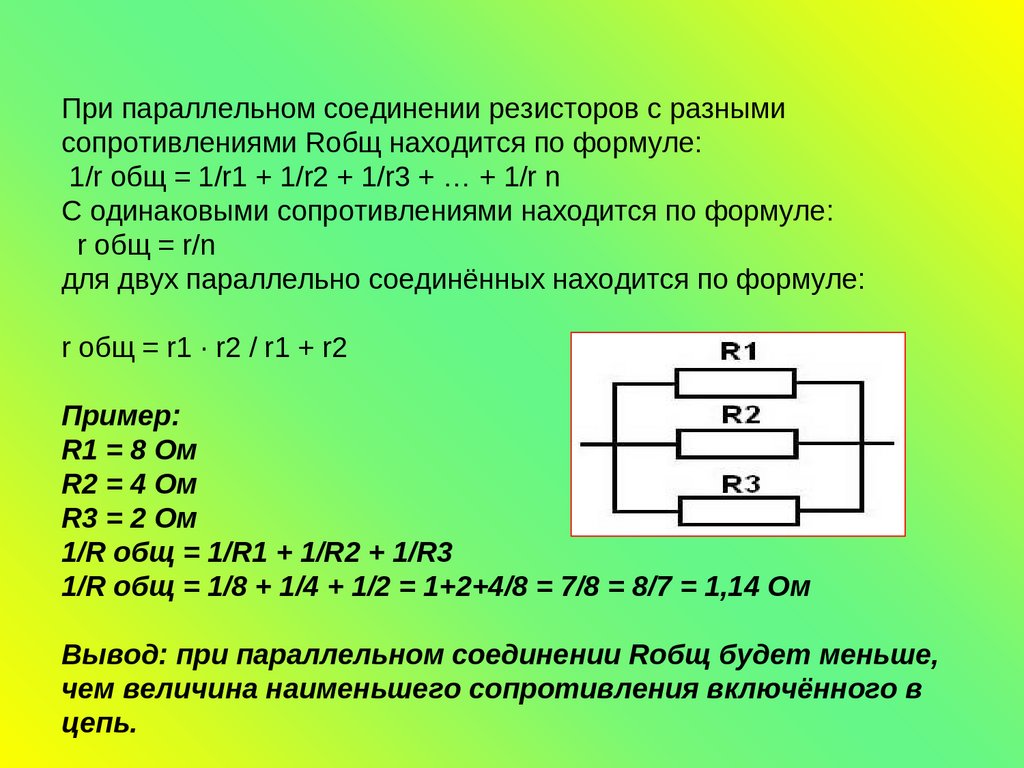 Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.
Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.
- Последовательное соединение
- Параллельное подключение
- Смешанный вариант
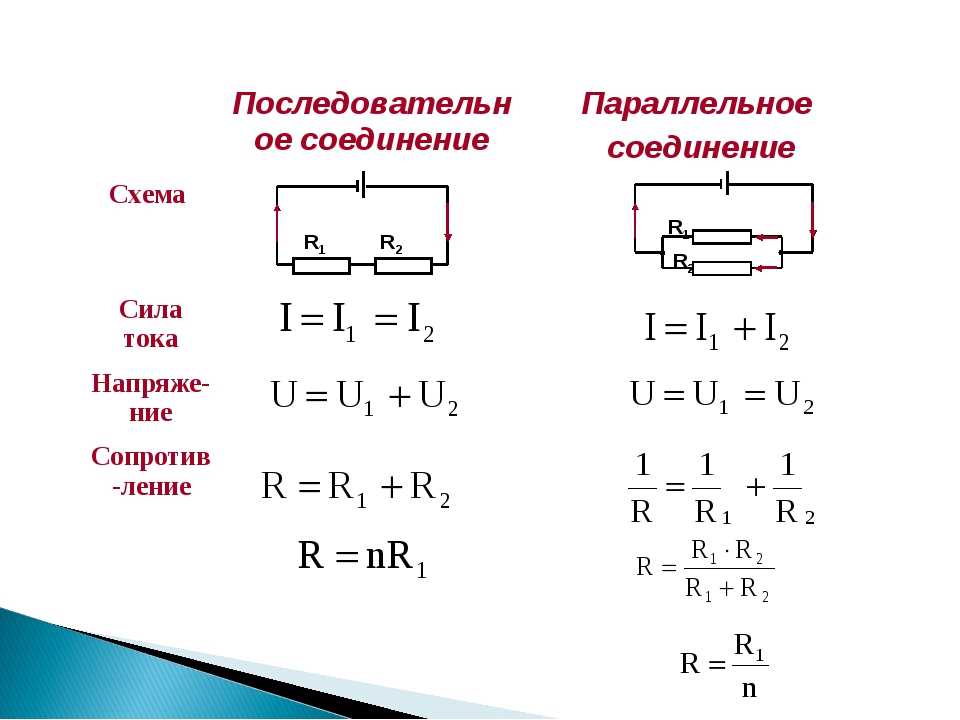
Последовательное соединение
Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.
От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:
- R общее — это сумма всех сопротивлений;
- R1 — первый резистор;
- R2 — второй компонент;
- Rn — последняя составляющая в цепи.

Параллельное подключение
Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой. Сами компоненты при этом расположены на одинаковом расстоянии друг от друга, а их количество не ограничено. По каждой составляющей электричество протекает отдельно, выбирая один из нескольких путей.
Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.
В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2).
Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.
Смешанный вариант
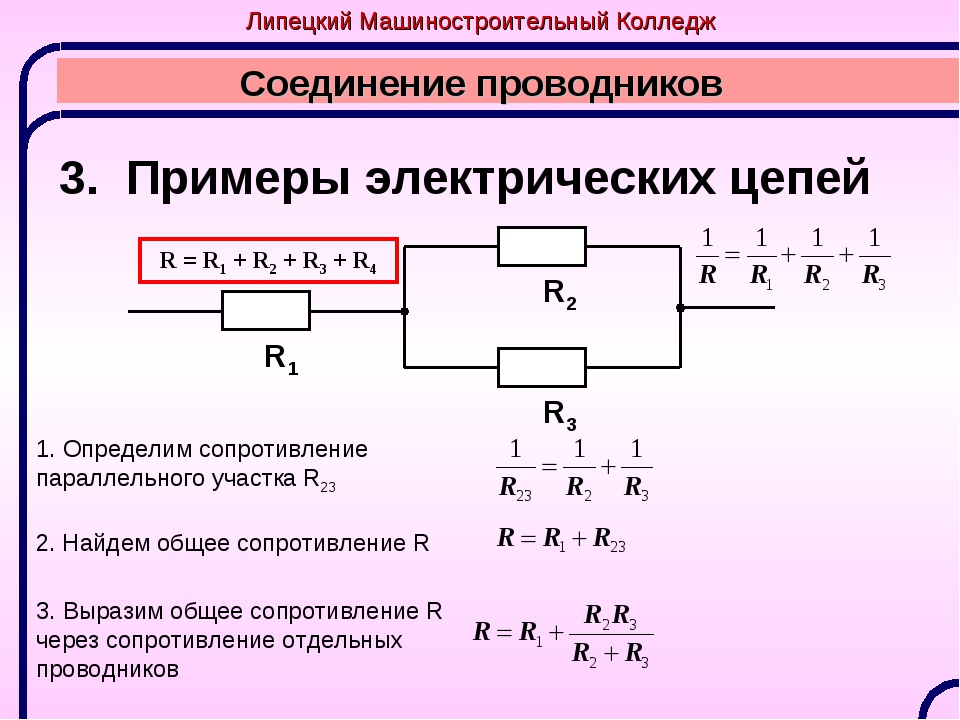
В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений. В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.
Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:
- в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
- после этого высчитывают противостояние на последовательно подключённых участках схемы;
- наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
- рассчитывают сопротивление в новой схеме по одной из двух формул.

Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.
Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.
В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.
Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.
На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.
Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.
Резисторы в параллельной формуле с решенными примерами
Когда резисторы используются в электронных схемах, они могут использоваться в различных конфигурациях. Определив способ организации резисторов, мы можем рассчитать сопротивление цепи или ее части.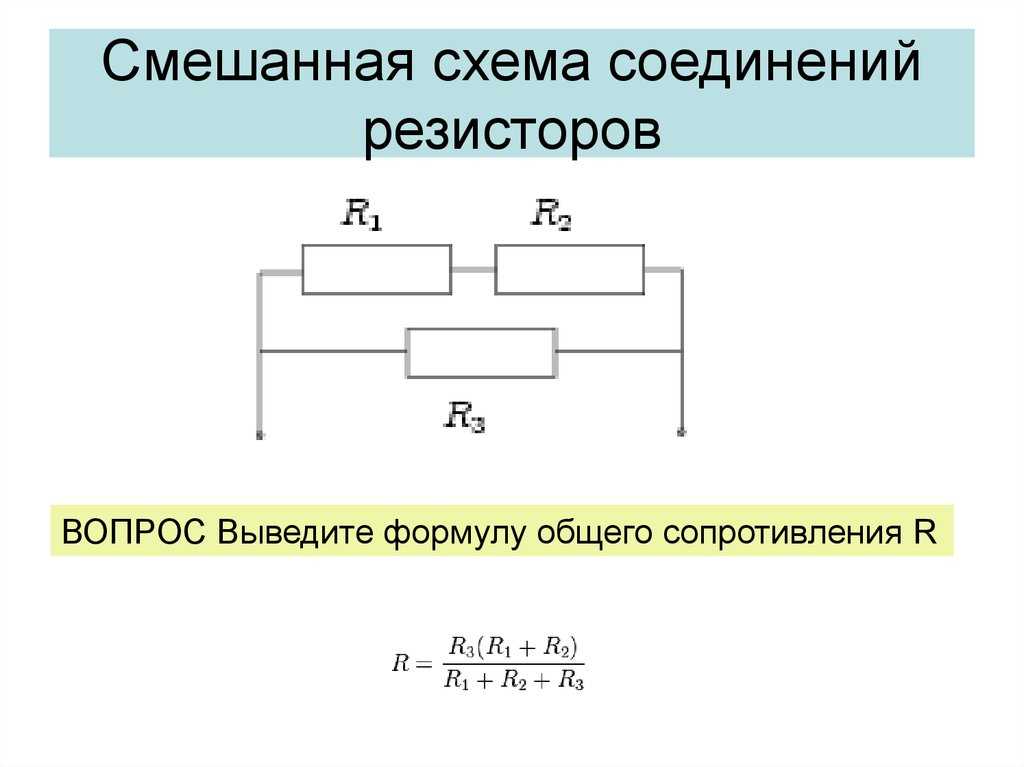
Когда два или более резистора соединены параллельно друг с другом в цепи таким образом, что оба вывода одного резистора соединены с каждым выводом другого резистора или резисторов, называются резисторами, включенными параллельно. Параллельная цепь имеет другое название — делитель тока. Это может позволить току цепи в параллельной сети резисторов проходить более чем по одному каналу, поскольку для него существует несколько путей. Следовательно, ток по всем ветвям параллельной сети неодинаков. С другой стороны, падение напряжения на всех резисторах в параллельной резистивной сети является постоянным.
Рассчитав эквивалентное сопротивление цепи, мы можем получить полное сопротивление параллельной цепи. Обратная величина эквивалентного сопротивления равна сумме обратных величин отдельных сопротивлений, соединенных параллельно, — это то, что представляет формула.
Символ Req используется для обозначения эквивалентного сопротивления. Ом (Ом)0014 Т -3 ].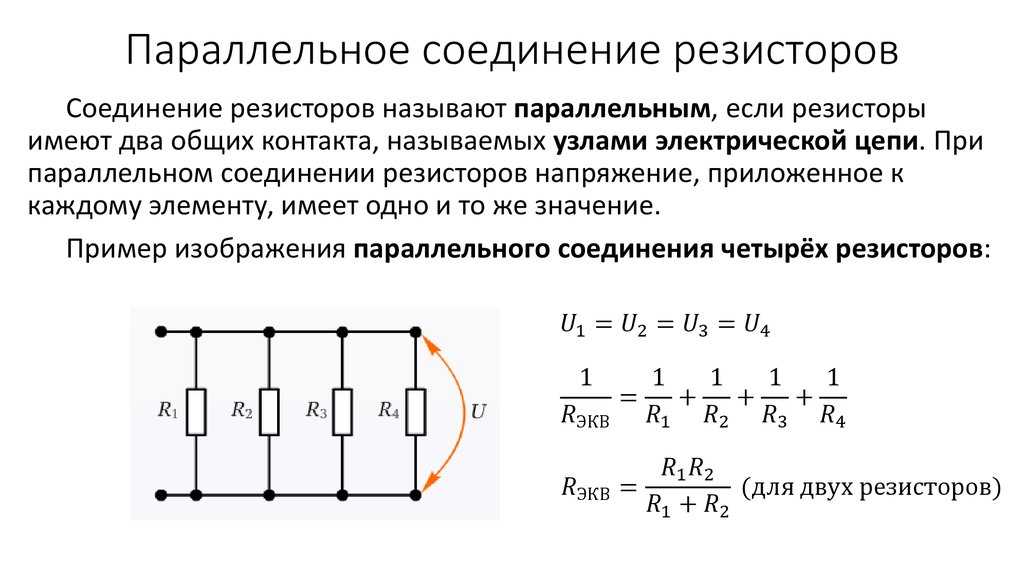
1/R Уравнение = 1/R 1 + 1/R 2 + 1/R 3 + …… + 1/R N
Где
R EQ EQ EQ означает эквивалентное сопротивление,
R 1 означает сопротивление первого резистора,
R 2 означает сопротивление второго резистора,
R 3 означает сопротивление третьего резистора и так далее.
Примеры резисторов в параллельном соединении формула
1) Когда три сопротивления 5 Ом, 2 Ом и 7 Ом соединены параллельно, рассчитайте эквивалентное сопротивление.
Решение:
Мы имеем,
R 1 = 5 ω
R 2 = 2 ω
R 3 = 7 ω
.
1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
1/R экв.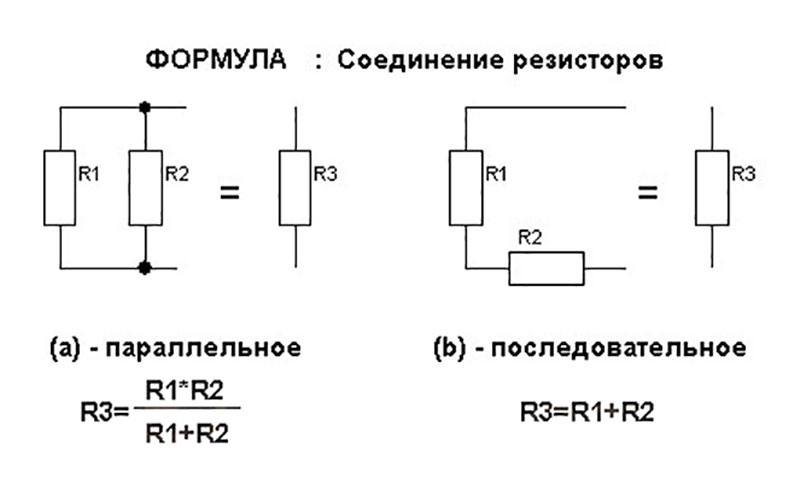 + 1/51 + 1/510003
+ 1/51 + 1/510003
1/R eq = 1/1,2
R eq = 1,2 Ом
.
Решение:
Дано
R 1 = 2 ω
R 2 = 1 Ом
R 3 = 3 ω
Получив форма, мы будем 1/R экв. = 1/R 1 + 1/R 2 + 1/R 3
= 1/2 + 1/1 + 1/3
= 1/0,55
R Уравнение = 0,55 ω
Формула натяжения
Сила, действующая на длину гибкого участка, такого как веревка, трос или цепь, называется силой формулы натяжения.
Сила, притягиваемая и передаваемая в осевом направлении с помощью веревки, троса, цепи или другого подобного одномерного непрерывного объекта, или каждого конца стержня или другого подобного трехмерного объекта; напряжение также может быть описано как пара сил действие-реакция, действующих на каждом конце вышеупомянутых элементов.
Сила натяжения
На латыни «натяжение» означает «растяжение». В физике сила, приложенная к длине гибкого участка, такого как веревка, кабель или цепь, известна как сила формулы натяжения. Мы знаем, что сила натяжения указывает на толчок или натяжение. В физике мы сталкиваемся с несколькими видами сил, такими как вес, нормальная сила, толчок и удар. В зависимости от того, как он работает и взаимодействует, сила или мощность могут быть контактными или бесконтактными. Сила натяжения представляет собой контактную силу, передаваемую отрезком гибкого материала.
Полная энергия равна: Fnet = T − W = 0
T = W ± ma
Если тело движется вверх, напряжение называется T = W + ma
- тело опускается T = W – ma
Напряжение, также известное как мощность пары «действие-противодействие», применяется к каждому компоненту адаптивного предмета.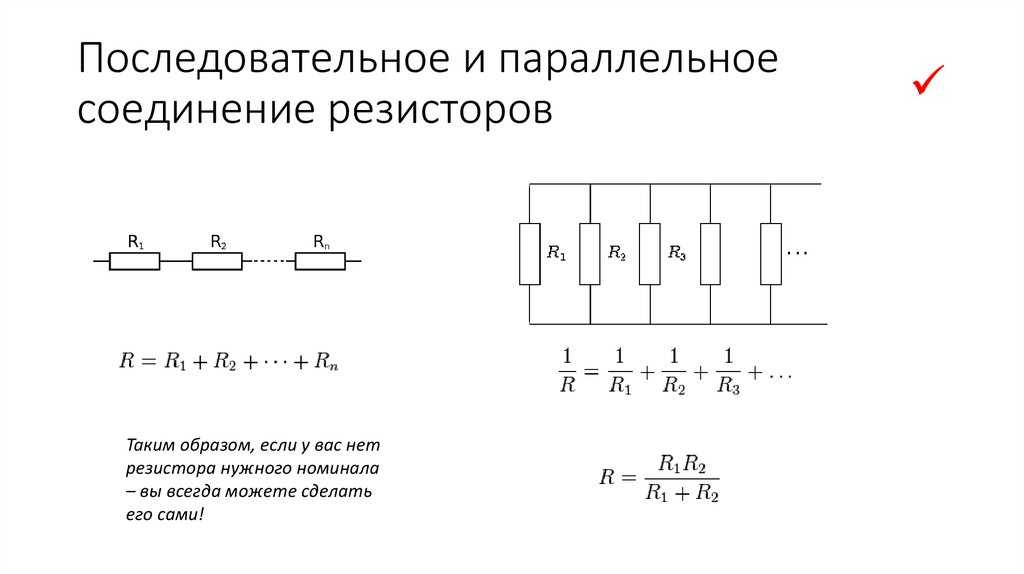 Если мы исследуем сшивание, то часть струны на одной стороне поперечного сечения будет использовать силу действия на часть струны на противоположной стороне поперечного сечения. Точно так же второй сегмент троса использует силу реакции предыдущего сегмента.
Если мы исследуем сшивание, то часть струны на одной стороне поперечного сечения будет использовать силу действия на часть струны на противоположной стороне поперечного сечения. Точно так же второй сегмент троса использует силу реакции предыдущего сегмента.
В каждом поперечном сечении силы растяжения видны с обеих сторон. На концах веревка будет оказывать давление на привязанный к ней предмет (гравитация), и объект будет использовать силу реакции веревки, чтобы подтянуться ближе к веревке. Направление этой силы коррелирует с длиной веревки.
Когда атомы или молекулы расходятся на атомном уровне и накапливают потенциальную энергию, в то время как восстанавливающая сила все еще присутствует, восстанавливающая сила может создавать напряжение.
В случае тел, подвешенных на цепи, тросе, веревке и т. д., натяжение может быть ясно объяснено. Он обозначается буквой T (иногда также обозначается как Ft).
Решаемые примеры
В.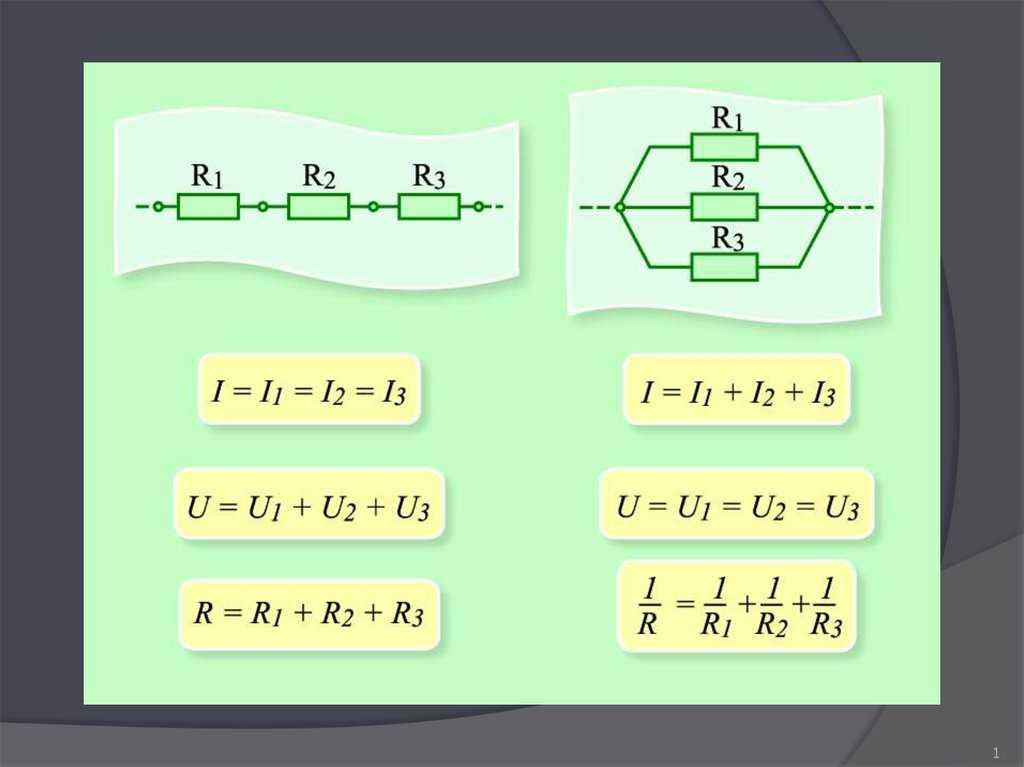
 Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.
Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.