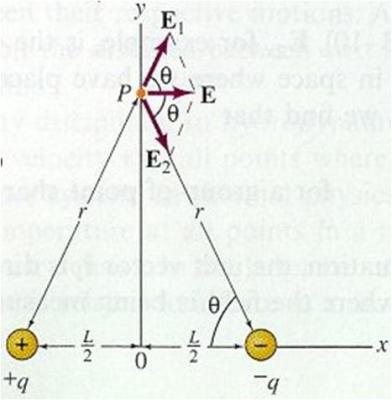
Важным свойством электрического поля, как поля не имеющего вихрей и созданного одними неподвижными источниками, является его потенциальность. Электрическое поле называется потенциальным, если работа, которую совершает носитель заряда в таком поле, при перемещении его по любому замкнутому контуру равняется нулю. Гравитационное поле силы тяжести также является потенциальным. Если поднять груз определенной массы на некоторую высоту, а затем опустить его обратно на поверхность Земли, в прежнюю точку, то полная механическая работа будет также равна нулю. Причем, совершенно не важно по какой траектории осуществлялся подъем и спуск груза. Источником такого гравитационного поля является в этом примере Земля (тело с массой во много раз большей чем масса поднимаемого груза). Электростатическое поле, то есть такое поле, которое образовано неподвижными электрическими зарядами, также обладает аналогичной потенциальностью. Работа носителя заряда при его перемещении по замкнутому контуру в электростатическом поле будет равняться нулю. Траектория такого перемещения замкнута и называется контуром и эта траектория может быть любого вида, принципиальное значение имеет ее замкнутость, а не форма. На рисунке изображены разные траектории движения заряда в электростатическом поле плоского конденсатора. Не имеет значения по какому маршруту двигался заряд (картинка слева), совершенная им работа будет одинаковой, то есть A1=A2=A3. На правом изображении показано движение заряда по замкнутому контуру. Начальная и конечная точки поля совпадают. Заряд двигался из точки 1, затем 2, 3, и снова прибыл в точку 1, тем самым образовав замкнутую траекторию, то есть контур. В этом случае говорят, что совершенная им механическая работа равна нулю. Так как электростатическое поле является потенциальным, то в нем каждая точка пространства имеет потенциал характеризующий это поле. Для гравитационного поля это будет гравитационный потенциал, а для электрического — электрический потенциал. Что же такое потенциал и как он определяется? Потенциалом φ точки электрического поля называется работа, которую нужно затратить, чтобы переместить заряд +q в количестве одного Кулона из бесконечности в данную точку поля, или же работа по перемещению этого же заряда +q из данной точки в бесконечность. Из определения потенциала получается, что потенциал — это показатель характеризующий работу заряда, то есть это по-сути энергетическая характеристика поля. Что же следует понимать под бесконечностью? Это всё-таки некоторое расстояние, а не математическое понятие ∞. Под бесконечностью в определении потенциала следует понимать такое расстояние в пространстве, на котором поле можно считать равным нулю, то есть напряженность поля в ней настолько мала, что ее можно принять за ноль. Силовые линии электрического поля одиночного заряда уходят в бесконечность и даже в этой бесконечности с противоположной стороны вполне может встретится заряд противоположного знака, и тогда эти две бесконечности встретятся. Вот такое место встречи и есть то место, где влияние поля одиночного заряда равно нулю. Это место нулевого потенциала, где потенциал φ=0, после перехода этой зоны нулевого потенциала его значения поменяют свой знак. В реальной природе, во вселенной, каждый заряд имеет свою противоположную пару и потому точка бесконечности — это точка равновесия, баланса. Из практических соображений бывает удобно принять некоторую линию или поверхность (эквипотенциальную) равной нулю. Это значит, что относительно некоторого источника электрического поля она всё же имеет некоторое значение, но принимается за ноль из практической необходимости. Получается обоснованная относительная система отсчета потенциалов поля. На этот счёт есть аналогия с гравитационным полем Земли (отсчет от уровня моря), когда влияние гравитации Солнца несущественно, но для высоких орбит космических спутников следует учитывать и гравитацию Солнца. При значительном приближении космического аппарата к Луне, влияние гравитационного потенциала Луны станет первостепенным и потребуется лунная система отсчета. Подобным образом обстоят дела и с электрическим полем Земли. Если в физике при рассмотрении теоретических вопросов выбирают бесконечность, то в электротехнике поступают иначе, и принимают за нулевой потенциал поверхность Земли. Соответственно на определенной высоте от поверхности Земли, в атмосфере, потенциал будет иметь некоторое отличное от нуля значение. В каком случае понятие потенциала теряет смысл? Если при движении заряда по разным траекториям будет совершатся разная работа, то есть она будет зависеть от формы пути, то здесь потенциал поля не имеет смысла. Итак, понятие потенциала относится только к потенциальному полю. Известное в механике понятие потенциальной энергии также относится к потенциальному полю. При отсутствии потенциального поля не может быть никакой речи о потенциальной энергии. Потенциальной энергией тела мы как раз и называем ту работу, которую необходимо затратить, чтобы переместить это тело из бесконечности в данную точку. Иначе говоря, требуется затратить энергию, чтобы перенести тело из области с нулевым потенциалом в область с высоким потенциалом. Опять же, если затрачиваемая работа зависит от формы пути, то нет потенциального поля, а значит невозможно говорить о потенциальной энергии. Как было уже сказано выше, потенциал — это энергетическая характеристика поля и потому достаточно легко определить потенциальную энергию через потенциал. Потенциальная энергия Up равна произведению заряда q на потенциал φ. Дата: 01.05.2015 © Valentin Grigoryev (Валентин Григорьев) Тег статьи: Электричество Все теги раздела Электротехника:Электричество Закон Ома Электрический ток Электробезопасность Устройства Биоэлектричество Характеристики Физические величины Электролиз Электрические схемы Асинхронные двигатели www.electricity-automation.com Известно, что силы гравитационного и электрического взаимодействия одинаково зависят от расстояния, векторы гравитационных и кулоновских сил при взаимодействии точечных тел направлены по прямой, соединяющей взаимодействующие тела. При перемещении тела между двумя точками в гравитационном поле работа силы тяжести не зависит от формы траектории его движения. Поэтому можно предположить, что при перемещении заряженной частицы в электростатическом поле из одной точки в другую работа сил электрического поля также не зависит от формы траектории. При перемещении частицы по замкнутой траектории эта работа равна нулю. Поле, работа сил которого по любой замкнутой траектории равна нулю, называется потенциальным полем. Гравитационное и электростатическое поля являются потенциальными полями. Работа сил в однородном электрическом поле. Докажем независимость работы сил электростатического поля от вида траектории движения заряда между двумя точками однородного поля. Пусть в однородном электрическом поле напряженностью электрический заряд q перемещается из точки В в точку D (рис. 1.23). Если бы заряд двигался по прямой BD, то работа сил электрического поля была бы равна , где S – модуль вектора перемещения, – угол между направлениями вектора кулоновской силы и вектора перемещения заряда . Если заряд из точки B сначала движется по прямой в точку C, а затем по прямой из точки C в точку D, то работа сил электрического поля по-прежнему будет равна . Действительно, . Таким образом, работа сил однородного электрического поля при перемещении электрического заряда по прямой BD и по ломаной BCD одинакова и равна произведению электрического заряда на напряженность электрического поля и расстояние, на которое переместился заряд вдоль линии напряженности электрического поля: . Любую кривую, соединяющую точки B и D в однородном электрическом поле, можно приближенно представить состоящей из последовательных отрезков, расположенных параллельно и перпендикулярно линиям напряженности. Применив такие же рассуждения для каждого участка траектории, получим, что полученное для работы выражение справедливо для вычисления работы сил однородного электрического поля при движении заряда по любой траектории. Работа сил в поле точечного заряда. Определим работу, которая совершается при перемещении заряда в электрическом поле, источником которого является точечный положительный заряд Q. Пусть положительный пробный заряд q находится сначала в точке M на расстоянии от заряда Q, а затем оказывается в точке N на расстоянии от заряда Q (рис. 1.24). Допустим также, что заряд двигался вначале вдоль радиуса по прямой MK, а затем по дуге KN окружности радиусом . Тогда работа по перемещению заряда из точки M в точку N равна сумме работ на участках MK и KN. Работа по перемещению заряда по дуге равна нулю, так как на этом участке векторы силы и перемещения перпендикулярны друг другу. Остается найти работу, совершаемую полем при перемещении пробного заряда вдоль радиуса, то есть вдоль линии напряженности. Но на этом участке в каждой точке сила, действующая на заряд со стороны электрического поля, принимает новое значение. Однако на очень малом отрезке пути вдоль линии напряженности элементарную работу сил электрического поля можно принять равной , где r – расстояние от источника поля до выделенного отрезка . Работу сил электрического поля при перемещении пробного заряда q из точки M, расположенной на расстоянии от заряда Q, в точку K, расположенную на расстоянии , можно найти как сумму элементарных работ на малых отрезках пути: . Операция нахождения такой суммы при переходе к бесконечно малым значениям перемещения называется интегрированием. Интегрирование в данном случае приводит к следующему результату: Легко показать, что если пробный заряд будет перемещаться по другой траектории, например, из точки M в точку L по дуге окружности, а затем вдоль радиальной прямой в точку N, то результат окажется таким же. Следовательно, работа сил поля точечного заряда по перемещению пробного заряда по произвольной траектории не зависит от формы траектории и определяется лишь положениями начальной и конечной точек, то есть поле точечного заряда является потенциальным. Но если действующие силы потенциальны, то работу этих сил можно представить как разность потенциальных энергий в начальной и конечной точках траектории: Сопоставление формул (1.6) и (1.7) приводит к следующему выражению для потенциальной энергии заряда q в поле заряда Q: Потенциальная энергия взаимодействия зарядов определяется с точностью до произвольного постоянного слагаемого, значение которого можно задать так, чтобы упростить решение задачи. Однако работа сил поля не зависит от этой произвольной постоянной, поскольку она определяется разностью потенциальных энергий. Значение постоянной интегрирования выбирается таким образом, чтобы при удалении заряда на бесконечность (то есть при ) потенциальная энергия обращалась в нуль. При этом условии получается, что . Таким образом, электростатическое поле потенциально, и любая заряженная частица в нем обладает потенциальной энергией. Разные пробные заряды будут обладать в одной и той же точке поля разной потенциальной энергией. Однако отношение потенциальной энергии к величине пробного заряда будет одним и тем же. Аналогично тому, как была введена силовая характеристика электрического поля – его напряженность, введем энергетическую характеристику электрического поля – потенциал: Потенциалом электрического поля в данной точке называется отношение потенциальной энергии, которой обладает пробный заряд, помещенный в данную точку поля, к этому заряду. Из (1.9) следует, что потенциал численно равен потенциальной энергии, которой обладал бы в данной точке поля единичный положительный заряд. Сравнив выражения (1.8) и (1.9), получим выражение для потенциала поля точечного заряда: . Потенциал определен с точностью до произвольной постоянной, зависящей от выбора нулевого уровня потенциала. Обычно полагают равным нулю потенциал поля в точке, удаленной бесконечно далеко от точечного источника поля; то есть при потенциал . При таком условии . Тогда выражение для потенциала поля точечного заряда имеет вид: . Рассмотрим поле, созданное системой N точечных зарядов . Расстояние от каждого заряда до данной точки поля обозначим . Работа, совершаемая силами этого поля над зарядом q, равняется алгебраической сумме работ сил, обусловленных каждым зарядом в отдельности: Сопоставив выражение (1.10) с выражением (1.7), получим для потенциальной энергии заряда q в поле системы зарядов выражение . Следовательно, при условии обращения потенциальной энергии в нуль на бесконечности, получаем: Таким образом, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. Из (1.9) следует, что заряд, находящийся в точке с потенциалом , обладает потенциальной энергией: . Следовательно, работа сил поля над зарядом q может быть выражена через разность потенциалов: Если заряд q из точки с потенциалом удалить на бесконечность (где по условию потенциал равен нулю), то работа сил поля будет равна: Отсюда следует, что потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля на бесконечность. Формулу (1.13) можно использовать для установления единиц потенциала. За единицу потенциала принимают потенциал в такой точке поля, для перемещения в которую бесконечно удаленного единичного положительного заряда необходимо совершить работу, равную единице. В системе единиц СИ единицу потенциала называют Вольтом, – это разность потенциалов двух точек электрического поля, при переходе между которыми заряда поле совершает работу : . В системе СГСЭ единица потенциала не имеет специального названия. megaobuchalka.ru Электростатическое поле точечного заряда – центральное, поэтому оно потенциально. В силу принципа суперпозиции потенциально любое электростатическое поле. Потенциальная энергия заряда в электростатическом поле (Wp) – физическая величина, равная работе электростатического поля при перемещении заряда из его положения на нулевой уровень. Как правило, в электростатике принимается, что нулевой уровень находится на бесконечности. Работа перемещения заряда в электростатическом поле равна изменению потенциальной энергии заряда, взятому с противоположным знаком: A = – (Wp2 – Wp1). Потенциал электростатического поля (j) – физическая величина, равная отношению потенциальной энергии заряда в поле к его значению. Потенциал – величина скалярная. За его единицу в системе СИ принимается вольт (1 В = 1 Дж/Кл). Принцип суперпозиции для потенциала. Потенциал электростатического поля, одновременно создаваемого в некоторой точке пространства несколькими зарядами, равна сумме потенциалов электростатических полей, которые создавались бы в этой же точке каждым из зарядов по отдельности j = j1 + j2 + ... . Эквипотенциальная поверхность – поверхность, во всех точках которой потенциал имеет одинаковые значения. Для поля точечного заряда эквипотенциальными поверхностями являются сферы с центром в точке расположения заряда. Работа электрического поля на криволинейном участке траектории . Циркуляция электростатического поля на замкнутой траектории . Потенциал электростатического поля точечного заряда . Потенциальная энергия взаимодействия двух зарядов . Потенциал электростатического поля (определение) . Связь работы электростатического поля с разностью потенциалов . Выражение потенциала поля через работу пробного заряда . Расчет потенциала по распределению напряженности поля . Расчет напряженности поля по распределению потенциала . Связь между напряжением и напряженностью для однородного поля . Дипольный момент электрического диполя . Момент сил, действующих на электрический диполь в электрическом поле ; . Потенциальная энергия электрического диполя во внешнем электрическом поле . Проводники – вещества, в которых имеются свободные заряды, способные перемещаться под действием электрического поля. Электростатическая индукция – явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле. Свободные заряды в проводнике, находящемся во внешнем электростатическом поле, перераспределяются так, что создаваемое ими собственное поле компенсирует внешнее, в результате чего напряженность результирующего поля в проводнике становится равной нулю. На этом явлении основана электростатическая защита – защита чувствительных к электрическому полю приборов с помощью замкнутой металлической оболочки, т. к. внутри нее электрическое поле отсутствует. Конденсатор – устройство для накопления значительных по величине разноименных электрических зарядов. Конденсатор состоит из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Электроемкость конденсатора – физическая величина, равная отношению заряда одной из пластин конденсатора (по модулю) к напряжению между его обкладками. Свойства электростатического поля внутри проводника . Свойства электростатического поля вне проводника около его поверхности . Электроемкость уединенного проводника (определение) . Электроемкость шара . Электроемкость конденсатора (определение) . Электроемкость плоского конденсатора . Электроемкость цилиндрического конденсатора . Электроемкость сферического конденсатора . Электроемкость параллельно соединенных конденсаторов . Электроемкость последовательно соединенных конденсаторов . Потенциальная энергия системы электрических зарядов . Потенциальная энергия уединенного проводника . Потенциальная энергия конденсатора . Объемная плотность энергии электрического поля . Условия на границе раздела двух диэлектриков ; . Плоский конденсатор Параллельное соединение Последовательное соединение studfiles.net Что такое электрический заряд? Какие виды зарядов Вы знаете? Электрический заряд — это связанное с телом свойство, позволяющее ему быть источником электрического поля и участвовать в электромагнитных взаимодействиях. Электрический заряд- количество электричества, содержащееся в данном теле. Самое простое и повседневное явление, в котором обнаруживается факт существования в природе электрических зарядов, — это электризация тел при соприкосновении. Способность электрических зарядов как к взаимному притяжению, так и к взаимному отталкиванию объясняется предположением о существовании двух различных видов зарядов. Один вид электрического заряда называют положительным, а другой — отрицательным. Разноимённо заряженные тела притягиваются, а одноимённо заряженные — отталкиваются друг от друга. Каково значение элементарного электрического заряда? Электрический заряд любой системы тел состоит из целого числа элементарных зарядов, равных 1,6×10−19 Кл в системе СИ или 4,8×10−10ед СГСЭ. е≈1,6021892*10-19 Сформулируйте закон Кулона. Сила взаимодействия двух точечных зарядов, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними. В чем измеряется поток электрического смещения и его плотность? Поток электрического смещения измеряется в кулонах и представляет поток количества электричества, коротко - электрический поток. Электрическая индукция (Кл / м2) - это плотность потока количества электричества, коротко - плотность электрического потока. Квант количества электричества - элементарный электрический заряд, таким образом, квант заряда - это просто квант количества электричества. Аналогично, магнитный поток измеряется в веберах, представляя поток количества магнетизма. Т.е. электрический заряд обладает количеством электричества в виде электрического потока, магнит обладает количеством магнетизма в виде магнитного потока. Что такое «Напряженность электрического поля?» Напряжённость электрического поля — силовая характеристика электрического поля; векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q: ; [В/м] Какие единицы измерения напряженности электрического поля вы знаете? В системе СИ — в Ньютонах на Кулон или в Вольтах на метр (В/м или V/m). Что такое потенциал электрического поля, в чем он измеряется? Потенциал электрического поля - энергетическая характеристика электрического поля; скалярная величина, равная отношению потенциальной энергии заряда в поле к величине этого заряда. В СИ потенциал электрического поля измеряется в вольтах( или Дж/ Кл) megaobuchalka.ru Электрический потенциал – это скалярная физическая величина, характеризующая напряжённость поля. Через параметр также выражается электрическое напряжение. Учёные давно ломают голову над субстанциями электрического и магнитного полей, но пока сие для них загадка, как и гравитация. существование не оспаривается, но суть неясна. Не секрет электричество люди знали задолго до нашей эры, а к изучению не стремились. Главные достижения по изучению электричества случились бы минимум на 20 лет раньше, нежели в действительности. До Эрстеда влияние провода с током на магнитную стрелку отмечал Джованни Доменико Романьози в 1802 году. Это подтверждённые официальными изданиями данные, а собственно событие, возможно, произошло раньше. Заслуга Эрстеда лишь в заострении внимания общественности на замеченном факте. Подобных примеров тьма. Порой учёные вне зависимости друг от друга делали открытия, изобретения. Встречались случаи, когда муж науки думал, что его измышления не новы. Потом удивлялся, когда оказывалось, что авторство теперь принадлежит постороннему человеку, хотя собственное открытие случилось раньше по времени. Замалчивание гарантировало переход доли известности к описавшему событие. Так происходило в XIX веке – учёные постоянно сотрудничали, что-то обсуждали, порой тяжело найти концы. К примеру, Фарадея упрекали за плагиат конструкции первого человеческого двигателя, а Википедия приписала ему авторство катушки индуктивности, придуманной Лапласом, на которое Майкл не претендовал. Впрочем, когда речь заходит о материи полей, учёные хранят дружное молчание. Единственным исключением стал Никола Тесла, утверждавший, что все во Вселенной состоит из гармонических колебаний. Итак, учёные не знают о поле ничего, а электрический потенциал это характеристика поля. Субстанцию никто не видел, долго не могли зарегистрировать и с трудом представляют поныне! Не верите — попробуйте нарисовать в воображении электромагнитную волну: Так выглядит современная физика. Никто точно не знает, как выглядят поле, колебание, волна, как это нарисовать. Понятно лишь: картинки из учебника слабо описывают происходящее. Дело усугубляется неспособностью человека видеть и чувствовать электромагнитное излучение. Колебание не выглядит синусоидальным, рассматривается для одной точки, линии, фронта и пр. Это, скорее, уплотнение и растяжение эфира, нечто напоминающее трёхмерную неописуемую фигуру. Длинное предисловие свидетельствует, насколько неизведанным остаётся то, что используется в повседневной жизни. И порой таит реальную опасность для человека. К примеру, доказано, что излучение СВЧ печи постепенно «портит» пищу. Человек, регулярно питающийся из микроволновки, рискует получить в собственное распоряжение обширный список недугов. В первую очередь — болезни крови. Небезопасна для людей и сетевая частота 50 Гц. Человек быстро понял, что электрическое поле есть, уже в XVIII веке – либо раньше – нарисована опилками его картина. Люди увидели линии, выходившие из полюсов. По аналогии стали пытаться изобразить электрическое поле. К примеру, Шарль Кулон на исходе восемнадцатого столетия открыл закон притяжения и отталкивания зарядов. Записав формулу, понял, что эквипотенциальные линии силы взаимодействия концентрически расходятся вокруг точечного скопления электричества, а траектории движения – прямолинейны. Так оказалась изображена первая картина электрического поля. Напоминает картину, как исследователи представляли магнитное, но с гигантской разницей: в природе нашлись заряды обоих знаков. Линии напряжённости уходят в бесконечность (в теории, безусловно, закончатся). А магнитные заряды поодиночке не найдены, линии их всегда замыкаются в видимой области пространства. Первая картина электрического поля В остальном нашлось много общего, к примеру, заряды одинакового знака отталкиваются, а разных – притягиваются. Это справедливо для магнитов и электричества. Гильберт заметил, что магнетизм – сильная субстанция, которую сложно экранировать или уничтожить, а электричество легко разрушается влагой и прочими веществами. Дёгтя в бочку добавил Кулон, который, следуя Бенджамину Франклину, присвоил электронам отрицательный заряд. Хотя речь шла о количестве флюида. И избыток электронов следовало назвать положительным. Как результат, линии напряжённости поля располагаются в направлении обратном правильному. Потенциал растёт не туда… Главными характеристиками электрического поля считаются: Наиболее вероятно происхождение терминов из латинского языка. Напряжённость ввёл в обиход, предположительно, Алессандро Вольта, а потенциал называется по наименованию типа поля, которое указанной величиной характеризуется: работа по перемещению заряда не зависит от траектории, равна разнице потенциалов начальной и конечной точки. Следовательно, на замкнутой траектории равна нулю. Электрическое поле считается потенциальным, значит, работа по перемещению в нем заряда не зависит от траектории и определяется единственно потенциалом. Потенциал — универсальное физическое понятие, часто применяемое. К примеру, для гравитационного поля Земли, происхождение которого поныне необъяснимо. Известно, что массы притягиваются по закону, напоминающему выведенный Шарлем Кулоном. Зарисовка напряжённости поля В электрическом поле Земной шар становится началом отсчёта. Нет разницы, относительно чего исчислять потенциал, но люди быстро поняли, что смоляное электричество бьётся, стеклянное кусается током, а грунт не причиняет вреда. Следовательно, в полном соответствии с логикой принят за нуль. В этом плюс: Земля громадная по объёму, на планету стекают без труда гигантские токи, статические и переменные. Доказано, что на теле заряд пытается распределиться взаимно на максимальной дистанции. Что соответствует поверхности планеты. При таком раскладе плотность заряда получается несущественной, много меньше, чем на любом наэлектризованном теле. На Земле потенциал за редким исключением измеряется относительно грунта, значение называют электрическим напряжением. Из контекста становится понятно, что напряжение бывает положительным и отрицательным. Впрочем, не всегда. На ЛЭП порой считается выгодным использовать схемы с изолированной нейтралью. Тогда потенциал любой точки не считается относительно Земли, отсутствует нейтраль. Это становится возможным в трёхфазных цепях. На местной подстанции ставят разделительный трансформатор, нейтраль вторичной обмотки которого заземляют, чтобы поставлять потребителям фазное напряжение 220 В, а не линейное. Порой люди наивно думают, что планета единая, следовательно, не нужна нейтраль, ток всё равно потечёт. Но потечёт через грунт, вызывая немалый экономический ущерб и представляя опасность для людей созданием шагового напряжения. Медный нулевой проводник – называли в первой половине XIX века возвратным – имеет малое сопротивление и гарантированно не причинит вреда. В цепях с изолированной нейтралью потенциал не отсчитывается относительно уровня грунта, а напряжение измеряется между двумя точками. Уместно упомянуть, что по закону Ома ток, протекая через проводник, создаёт разность потенциалов. Поэтому нельзя браться при аварии за контур заземления. Малое сопротивление способно оказаться причиной образования здесь немалой разницы потенциалов. А человек обязан помнить об опасности напряжения прикосновения. Однако цепи с изолированной нейтралью используются и в целях безопасности. Если напряжение создаётся между двумя точками вторичной обмотки разделительного трансформатора, ток на землю через неосторожно взявшегося за оголённый провод человека не пойдёт — разница потенциалов относительно грунта меньше. Следовательно, разделительный трансформатор становится мерой защиты и часто используется на практике. Внешней электрической цепью называется участок, находящийся за пределами источника. На практике ЭДС вырабатывается на вторичных обмотках трёхфазного трансформатора подстанции, считаясь источником. Начиная с вывода, идёт внешняя цепь. На ней потенциал падает от фазного напряжения до нейтрали. Речь идёт о рядовых потребителях. Когда в дом приходит электричество, это неизменно система трёхфазного тока. Нейтраль глухо заземлена, чтобы обеспечить нужный уровень безопасности. Жилой дом не гарантирует равномерную загрузку всех фаз, через нейтраль потечёт ток. Если цепь использовать для защиты, не возникает полной гарантии безопасности: путь тока способен пролечь через человека, неожиданно взявшегося за заземлитель. Следовательно, нужно обеспечить два нулевых проводника: рабочий и защитный. Через первый производится зануление металлических частей объекта, через второй – заземление. Причём за рубежом принято делить две ветви на две разные линии, а в РФ они объединяются в районе контура заземления. Первое сделано для надёжной защиты, второе – для возможности работы в здании трёхфазного оборудования (вдруг пригодится!). Если в промышленной установке оставить лишь заземление корпуса, это плохо окончится для неудачника, попавшего под электрический потенциал. Следовательно, западная система хороша для однофазного оборудования. Но за счёт унифицированности система РФ сложнее. Импортное оборудование плохо сочетается с российскими условиями: фильтры питания рассчитаны так, чтобы защитный и рабочий нулевые проводники не пересекались. Причина в электрическом потенциале: Система TN-C-S Чтобы выровнять разницу, линии на входе в здание объединяют и заводят на контур громоотвода. Что для импортной техники не становится идеальным решением, предприятия-поставщики электроэнергии несут потери. Это известная система TN-C-S, применяющаяся в РФ. Дома, возведенные ещё в СССР, понемногу переоборудуются. vashtehnik.ru По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Электрическое поле одного тела оказывает силовое действие на другое заряженное тело, и наоборот. Электрическое поле - это особая форма материи, через которую осуществляется взаимодействие электрических зарядов. Оно существует реально, независимо от нас и от наших знаний о нём. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Электрическое поле, окружающее заряженное тело, можно исследовать с помощью пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика электрического поля - напряженность. Напряженность электрического поля – это векторная физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля, и направленная в сторону действия силы. Напряженность электрического поля равная отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку поля, к величине этого заряда Напряженность электрического поля – векторная физическая величина, т.е. имеющая направление. Направление вектора Если поле создано положительным зарядом, то для того, чтобы определить направление вектора напряженности в т.А, мы мысленно помещаем в т.А положительный пробный заряд. Одноименно заряженные тела отталкиваются, поэтому сила, действующая на пробный заряд, а значит и вектор напряженности направлены от заряда, создающего поле. Если поле создано отрицательным зарядом, то для того, чтобы определить направление вектора напряженности в т.А, мы мысленно помещаем в т.А положительный пробный заряд. Разноименно заряженные тела притягиваются, поэтому сила, действующая на пробный заряд, а значит и вектор напряженности направлены к заряду, создающему поле. Направление вектора Электрическое поле, которое создается неподвижным электрическим зарядом называются электростатическим. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от него, равна по модулю Электрическое поле, векторы напряженности которого одинаковы во всех точках, называется однородным. Если электрическое поле создается несколькими заряженными телами, то выполняетсяпринцип суперпозиции (наложения) полей точечных зарядов: напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами по отдельности: Для наглядного представления электрического поля используют силовые линии. Силовой линией или линией напряженности называется такая линия, в каждой точке которой вектор напряженности поля направлен по касательной к ней. Эти линии проводятся так, чтобы направление вектора в каждой точке совпадало с направлением касательной к силовой линии: При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля. Силовые линии полей положительных и отрицательных точечных зарядов изображены на рисунках: в) силовые линии двух равных положительных зарядов Силовые линии однородного поля параллельны. Линии напряженности электрического поля: 1) никогда не пересекаются;2) не могут быть замкнуты сами на себя;3) имеют начало на положительном заряде (или в бесконечности) и заканчиваются на отрицательном заряде (или в бесконечности). При перемещении пробного заряда q в электрическом поле электрические силысовершают работу. Эта работа при малом перемещении Электростатическое поле обладает важным свойством: Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда. Следствием независимости работы от формы траектории является следующее утверждение: Работа сил электростатического поля при перемещении заряда по любой замкнутой траектори и равна нулю. Силовые поля, обладающие этим свойством, называют потенциальнымиили консервативными. Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая начальная точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю. Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной начальной точки (0) равна работе A10, которую совершит электрическое поле при перемещении заряда q из точки (1) в точку (0): Wp1 = A10 (В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.) Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора начальной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства. Потенциальная энергия заряда q, помещенного в электрическое поле, пропорциональна величине этого заряда. Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля: Потенциал φ является энергетической характеристикой электростатического поля. Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек: A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2) Разность потенциалов φ1 – φ2 называется напряжением между точками 1 и 2 и обозначается U12или просто U U = А/q Напряжение между двумя точками поля численно равно работе сил поля по перемещению единичного заряда q между этими точками. Значит А = qU Работа сил поля при перемещении заряда q между двумя точками поля прямо пропорциональна напряжению между этими точками. В Международной системе единиц (СИ) единицей потенциала и напряжения является вольт(В). 1В = 1Дж/1Кл Во многих задачах электростатики при вычислении потенциалов за начальную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность. Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов: φ = φ1 + φ2 + φ3 + ... Для наглядного представления электрического поля наряду с силовыми линиями используютэквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей. В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Свойства эквипотенциальных поверхностей: Электрическое поле имеет две характеристики: силовую (напряженность) и энергетическую(потенциал). Найдем связь между ними. Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно найти работу поля по перемещению этого заряда: ΔA12 = qEΔl и ΔA12 = – q(φ2 – φ1) = – qΔφ = q(φ1 – φ2) = qU, где φ1 – φ2 разность потенциалов. qEΔl = qU E = U / Δl = (φ1 – φ2) / Δl Здесь l – координата вдоль силовой линии. Это соотношение в скалярной форме выражает связь между напряженностью поляи потенциаломили напряжением: напряженность однородного поля численно равна разности потенциалов на единице длины линии напряженности. Поле сильнее там, где быстрее изменяется потенциал. Из этой формулы можно получить единицу напряженности в СИ. Она имеет наименование вольт не метр [В/м] infofiz.ru Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже). Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда: Напряжённость электростатического поля E{\displaystyle \mathbf {E} } и потенциал φ{\displaystyle \varphi } связаны соотношением[1] или обратно[2]: Здесь ∇{\displaystyle \nabla } — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком. Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля ∇⋅E=ρε0{\displaystyle \mathbf {\nabla } \cdot \mathbf {E} ={\rho \over \varepsilon _{0}}}, легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ: где φ{\displaystyle \varphi } — электростатический потенциал (в вольтах), ρ{\displaystyle \rho } — объёмная плотность заряда (в кулонах на кубический метр), а ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная (в фарадах на метр). Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как: где: При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении). Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произволом выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»). В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT−3I−1). В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг. Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ. Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов. Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения. Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния 1r{\displaystyle {\frac {1}{r}}} (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния. Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме: где k{\displaystyle k} обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ: q{\displaystyle q} — величина заряда, r{\displaystyle r} — расстояние от заряда-источника до точки, для которой рассчитывается потенциал. wikiredia.ruЭлектричество и автоматизация. Потенциал электрического поля это
Потенциал электрического поля
Электротехника: Основы
Потенциал электрического поля
Потенциальность поля

Потенциал
Потенциальная энергия

Потенциал электрического поля — Мегаобучалка
Рис. 1.24
.
(1.6)
.
(1.7)
.
(1.8)
.
(1.9)
.
(1.10)
.
(1.11)
.
(1.12)
.
(1.13)
Потенциал электрического поля
Проводник в электростатическом поле
Что такое потенциал электрического поля, в чем он измеряется? — Мегаобучалка
Электрический потенциал: характеристики, поле, особенности
Физический смысл электрического поля
Характеристики электрического поля

Нулевой потенциал и потенциальное поле
Падение потенциала во внешней электрической цепи

Лекция 25-1. Электрическое поле. Потенциал.
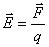
 совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд помещенный в данную точку поля.
совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд помещенный в данную точку поля.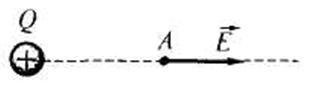

 зависит от знака заряда q создающего электрическое поле:
зависит от знака заряда q создающего электрическое поле: направлен по радиусу от заряда;
направлен по радиусу от заряда;
 направлен к заряду.
направлен к заряду.
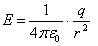

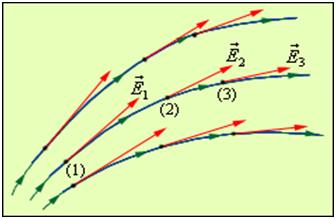
 а) силовые линии кулоновских полей (полей точечных зарядов)
а) силовые линии кулоновских полей (полей точечных зарядов) б) силовые линии двух равных положительного и отрицательного зарядов
б) силовые линии двух равных положительного и отрицательного зарядов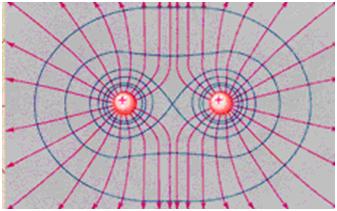
 равна
равна 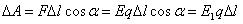
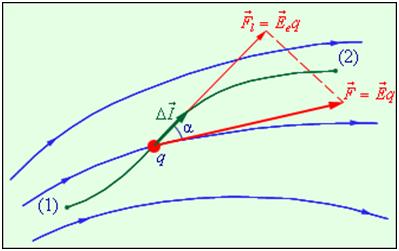 Работа электрических сил при малом перемещении
Работа электрических сил при малом перемещении  заряда q.
заряда q.
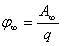
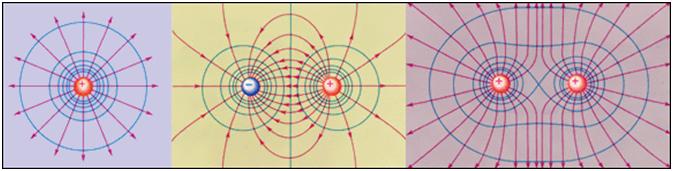 Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей
Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полейПотенциал электрического поля Википедия
У этого термина существуют и другие значения, см. Потенциал. Неоднозначность определения потенциала
Единицы измерения
Использование термина
Кулоновский потенциал
См. также
Примечания
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: