Содержание
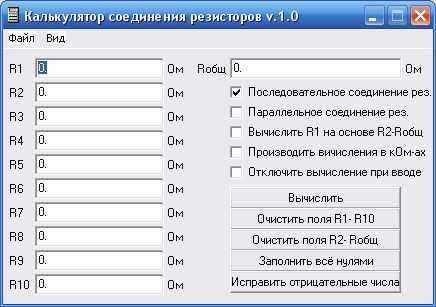
Последовательное и параллельное соединение проводников, резисторов,конденсаторов и катушек индуктивности. Онлайн расчёт.
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно.
Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным
да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»
Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно
набросаю пару-тройку калькуляторов на заданную тему.
Итак.
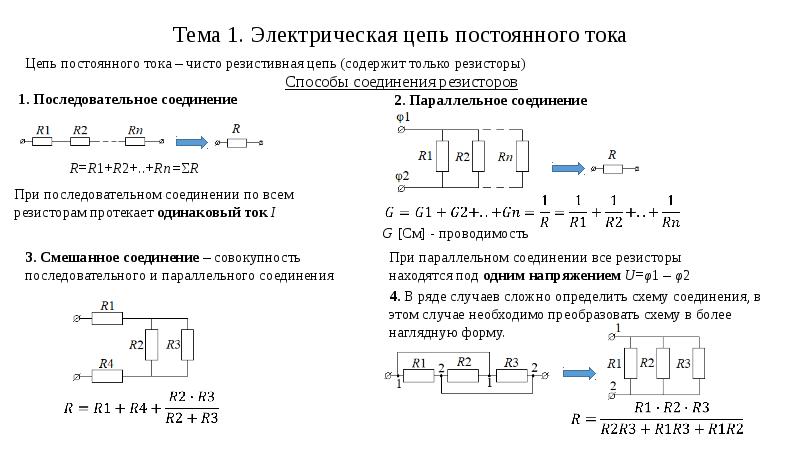
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи
равно сумме напряжений на концах каждого из проводников.
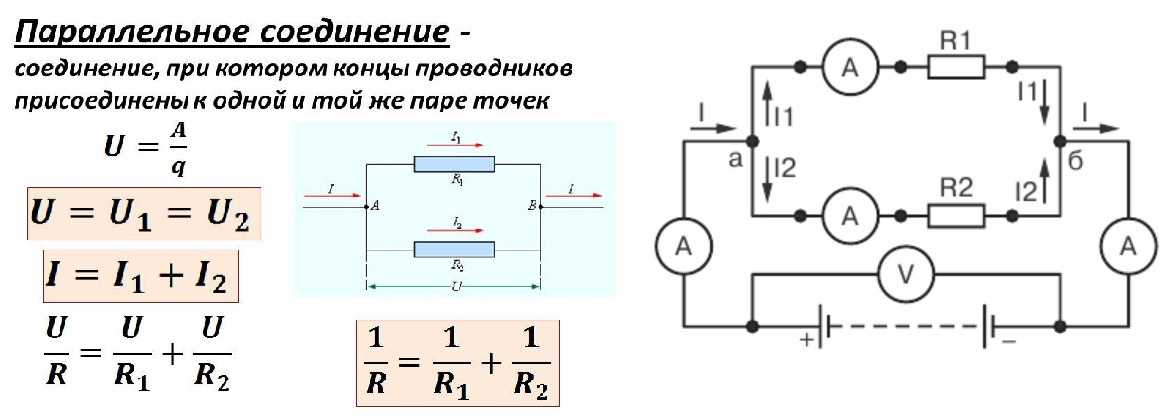
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для
всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то
оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном
соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
|
Тип соединения |  
ПараллельноеПоследовательное | |
|
Сопротивление резистора R1 |
|
ОмкОм МОм |
|
Сопротивление резистора R2 |
|
ОмкОм МОм |
|
Сопротивление резистора R3* |
|
ОмкОм МОм |
|
Сопротивление резистора R4* |
|
ОмкОм МОм |
|
Общее напряжение в цепи (В)* |
| |
|
| ||
|
Общее сопротивление цепи R |
| |
|
Общий ток в цепи I |
| |
|
Напряжение на резисторе R1 (U1) |
| |
|
Ток через резистор R1 (I1) |
| |
|
Напряжение на резисторе R2 (U2) |
| |
|
Ток через резистор R2 (I2) |
| |
|
Напряжение на резисторе R3 (U3) |
| |
|
Ток через резистор R3 (I3) |
| |
|
Напряжение на резисторе R4 (U4) |
| |
|
Ток через резистор R4 (I4) |
|
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение
напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность,
а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную
зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и
катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения
реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников
и резисторов.
А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и
параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2+….+ Сn и
1/L = 1/L1+ 1/L2 +…+ 1/Ln
для параллельных цепей и
L = L1 + L2 +….+ Ln и
1/С = 1/С1+ 1/С2+…+ 1/Сn для последовательных.
Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
|
Тип соединения |  
ПараллельноеПоследовательное | |
|
Ёмкость конденсатора С1 |
|
пФнФ МкФ |
|
Ёмкость конденсатора С2 |
|
пФнФ МкФ |
|
Ёмкость конденсатора С3* |
|
пФнФ МкФ |
|
Ёмкость конденсатора С4* |
|
пФнФ МкФ |
|
| ||
|
Общая ёмкость цепи С |
|
Ну и в завершении ещё одна таблица.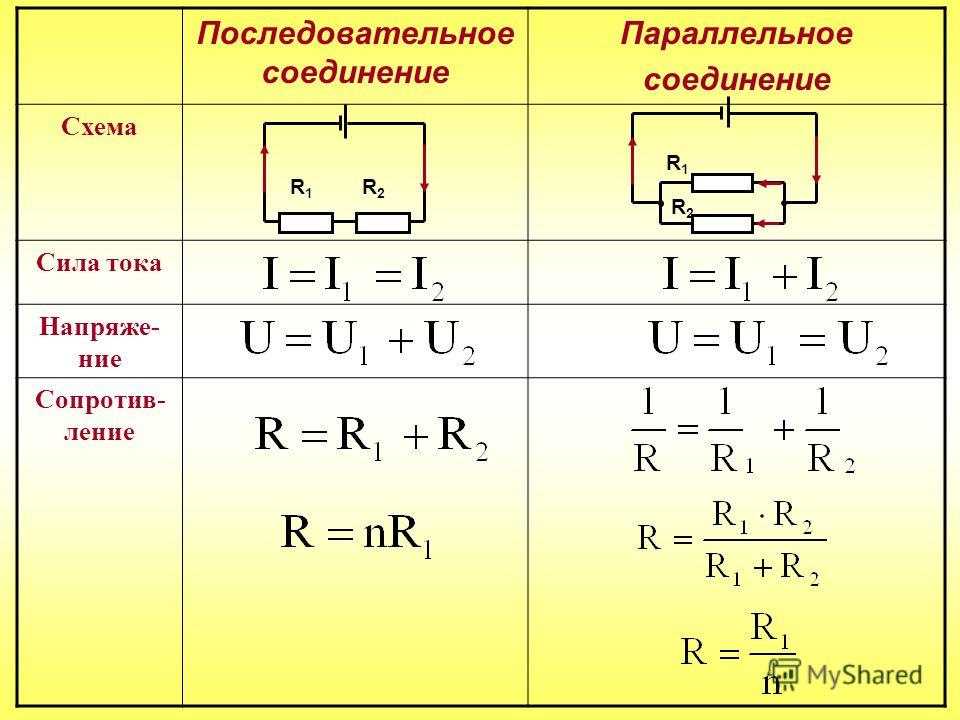
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
|
Тип соединения |  
ПараллельноеПоследовательное | |
|
Индуктивность катушки L1 |
|
мкГнмГн Гн |
|
Индуктивность катушки L2 |
|
мкГнмГн Гн |
|
Индуктивность катушки L3 |
|
мкГнмГн Гн |
|
Индуктивность катушки L4 |
|
мкГнмГн Гн |
|
| ||
|
Общая индуктивность цепи L |
|
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек,
то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание,
пересечения взаимных магнитных полей.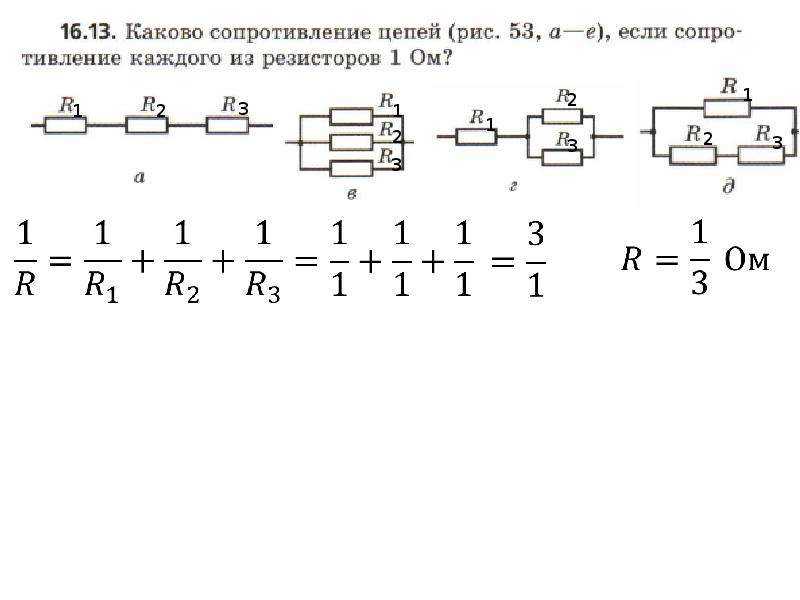
Параллельное и последовательное соединение резисторов (сопротивлений)
Все разнообразие схем построено на двух типах соединения — параллельном и последовательном. Для разных соединений действуют разные законы, что и дает возможность создания устройств с различными характеристиками. Рассмотрим последовательное и параллельное соединение резисторов.
Содержание статьи
- 1 Что такое резистор и для чего он нужен
- 2 Последовательное соединение сопротивлений
- 2.1 Теоретическая часть
- 2.2 Примеры расчета
- 3 Параллельное соединение резисторов
- 3.1 Теория и законы параллельного соединения
- 3.2 Примеры расчета параллельного соединения сопротивлений
- 4 Смешанное соединение
- 5 Практическое применение параллельного и последовательного соединения резисторов
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.
Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.
Последовательное соединение сопротивлений
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
При подключении полученной цепочки к источнику тока получается кольцо.
Лампы накаливания соединенные последовательно, можно рассматривать как сопротивления
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Последовательно соединенные сопротивления. I1 — ток протекающий через резистор R1, I2 — ток протекающий через резистор R2
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают.
R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается.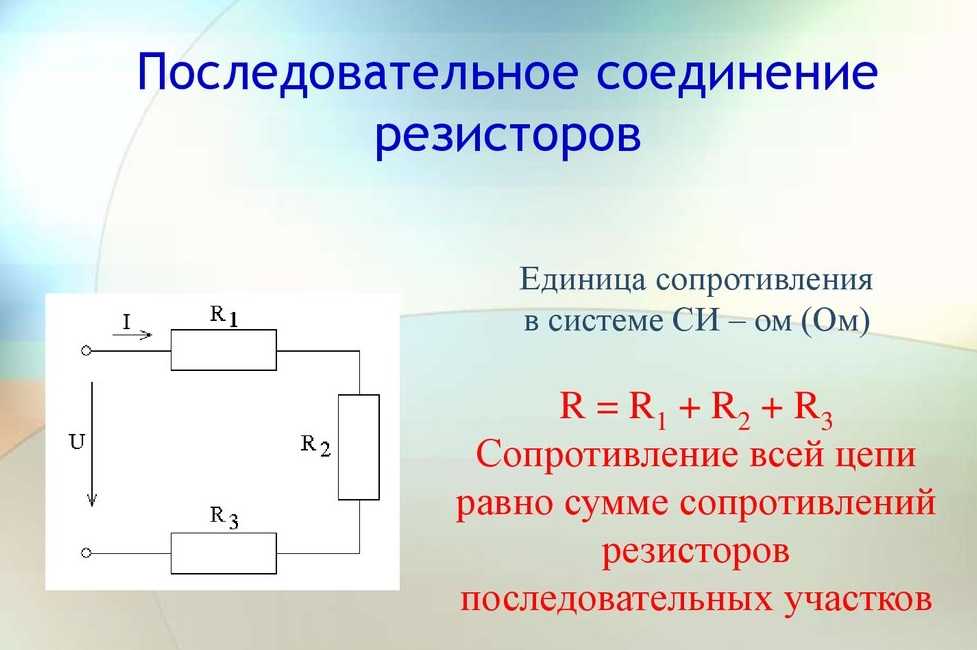 Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В.
Так понятнее, что такое последовательное соединение
Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом. Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В.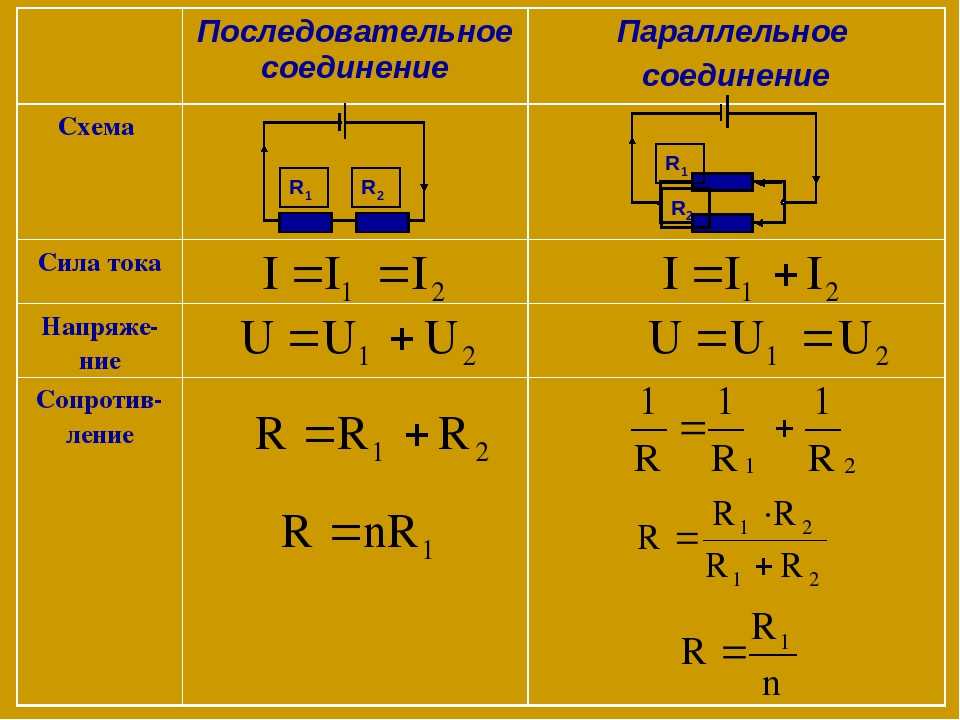 При этом напряжение источника питания — 4000 В.
При этом напряжение источника питания — 4000 В.
Параллельное соединение резисторов
Параллельное соединение — это когда входы нескольких деталей соединяются в одной точке. Точно так же — в одну точку — соединяют их выходы.
Так выглядит параллельное соединение на схеме и в реальности
Теория и законы параллельного соединения
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение. То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение.
U = U1 = U2 = U3.
Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Так выглядит параллельное соединение резисторов на схеме
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле:
1/R = 1/R1 + 1/R + 1/R3+…
Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Формулы расчета сопротивления при параллельном подключении двух и трех резисторов
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала.
Примеры расчета параллельного соединения сопротивлений
Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.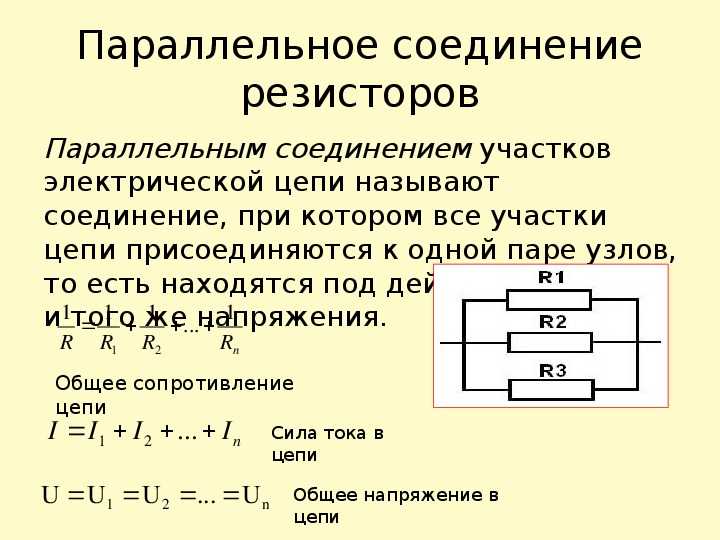
- Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом.
- Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом.
Еще один пример с лампочками
При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее. Но картина не отличается:
- Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом.

- Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом.
Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Смешанное соединение
Как быть, если в схеме есть и параллельное, и последовательное соединение резисторов? В таком случае считают общее сопротивление по участкам. Можно при этом перерисовывать схему, заменяя составные сопротивления на один «прямоугольник», но проставляя над ним высчитанный результат.
Пример расчета сопротивления при смешанном соединении резисторов. Рассматриваем исходную схему как совокупность параллельных и последовательных соединений
Шаг 1. Нашли общее сопротивление последовательно соединенных резисторов R3 и R4:
R3-4 = 3 кОм + 3 кОм = 6 кОм;
Шаг 2. Рассчитали сопротивление параллельно соединенных резисторов R2 и R3-4:
R2-4 = 3 кОм * 6 кОм / (3 кОм + 6 кОм) = 18 кОм/9 кОм = 2 кОм;
Шаг 3. Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
Рассчитали общее сопротивление последовательно соединенных резисторов R1 и R2-4:
R1-4 = R1 + R2-4 = 1 кОм + 2 кОм = 3 кОм.
Практическое применение параллельного и последовательного соединения резисторов
Для чего практически можно использовать параллельное и последовательное соединение резисторов? Случается, что при ремонте электронной аппаратуры, не всегда в наличии сопротивление нужного номинала. Ехать в магазин за одним копеечным элементом — накладно. Вот тут и могут пригодиться составные резисторы. Просто надо последовательно или параллельно соединить их, подобрав требуемый номинал.
Последовательное и параллельное соединение резисторов применяют для подбора требуемого номинала. Контролировать точное значение получившегося сопротивления можно при помощи цифрового мультиметра
При соединении резисторов, их ножки первоначально скручивают. Какой стороной разворачивать сопротивление — неважно (в отличие от диодов, резисторы одинаково пропускают ток в обоих направлениях). На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.
На концах скрутку слегка обжимают плоскогубцами, затем пропаивают. Следите за тем, чтобы корпуса были друг от друга подальше — так они будут лучше охлаждаться при работе.
резисторов в параллельных схемах
Сумма токов в параллельной сети можно рассчитать как
I = I 1 + I 2 + … + N (1)
где
I n = параллельный ток (ампер)
I = сумма токов (ампер)
можно рассчитать как общее сопротивление в параллельной цепи0003
1 / R = 1 / R 1 + 1 / R 2 + … + 1 / R N (2)
, где
R N =. параллельное сопротивление (Ом, Ом)
R = общее сопротивление в параллельной сети (Ом, Ом)
- с тремя резисторами R 1 = 10 Ом, R 2 = 20 Ом и R 3 = 30 Ом можно рассчитать как
1 / R = 1 / (10 Ом) + 1 / (20 Ом) + 1 /(30 Ом)
= 0,183 (1 /ω)
R = 1 /0,183
= 5,46 (ω)
Подключен к 12 V Батарея.
токов можно рассчитать
I = U / R
= (12 В) / (5,46 Ом)
= 2,2 ампер)
Тока через каждый резистор можно рассчитать как
I 1 = U / R 1
= (12 В) / (10 ω)
= 1,2 (AMPS)
I 2 = U / R 2
= (12 В) / (20 Ом)
= 0,6 (AMP)
= 0,6 (AMP)
= 0,6 (AMP)
= 0,6 (AMP) я 3 = U / R 3
= (12 В) / (30 Ом)
= 0,4 (AMP)
Резист 1 — 100 ohm
Resulting Resistance (Ω) R2
( Ω )R1 ( Ω ) 1 1.5 2.2 3. 3
4.7 6.8 10 15 22 33 47 68 1 0.5 0.6 0.69 0.77 0.83 0.87 0.91 0.93 0.95 0.97 0.98 0.99 1.5 0.6 0.75 0.89 1.03 1.14 1.22 1.30 1.36 1.40 1.43 1.45 1.46 2.2 0.69 0.89 1.1 1.32 1.50 1.66 1,82 1,92 2,0 2,06 2,10 2,13 3,3 0,777779
3,3 0,7777777777779779797979797979797
3,3 0,7,7777777777779797
3,3 0,7777777777777777777777777777777777777777777797
. 2 1.32
1.65 1.94 2.22 2.48 2.70 2.87 3.00 3.08 3.14 4.7 0.83 1.14 1.50 1.94 2.35 2.78 3.20 3.58 3.87 4.12 4.27 4.39 6.8 0.87 1.22 1.66 2.22 2.78 3.40 4.05 4.68 5.19 5.64 5.94 6.18 10 0.91 1.30 1.82 2.48 3.20 4.05 5.0 6.0 6.9 7.7 8.3 8.7 15 0.93 1.36 1.92 2.70 3. 58
4.68 6.0 7.50 8.9 10.3 11.4 12.2 22 0.95 1.40 2.00 2.87 3.87 5.19 6.9 8.9 11.0 13.2 15.0 16.6 33 0.97 1.43 2.06 3.0 4.12 5.64 7.7 10.3 13.2 16.5 19.4 22.2 47 0.98 1.45 2.1 3.08 4.27 5.94 8.3 11.4 15.0 19.4 23.5 27.8 68 0.99 1.46 2.13 3.14 4.39 6.18 8. 7
12.2 16.6 22.2 27.8 34.0 Download and print Resistors in parallel chart
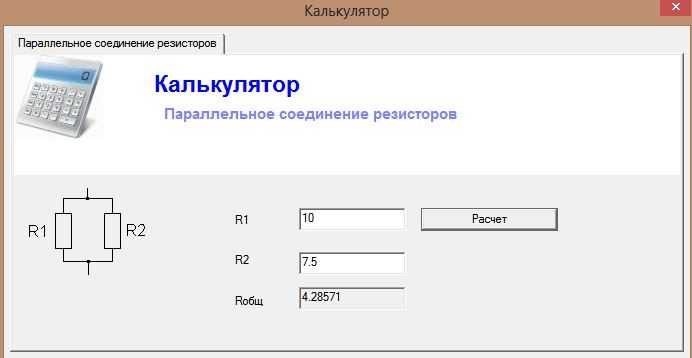
Калькулятор трех параллельных резисторов: подключение и формула
Вам нужен калькулятор трех параллельных резисторов ? Вам повезло, вот один, чтобы получить эквивалентное сопротивление этой конфигурации резисторов в цепи.
Его работа очень проста, и все, что вам нужно сделать, это записать сопротивление в омах каждого из трех резисторов и, когда оно у вас есть, нажать кнопку расчета, чтобы получить результат мгновенно, без необходимости ручных вычислений.
Разделы статей
- Параллельное соединение резисторов
- Расчет параллельных резисторов: формула
- Решаемое упражнение на параллельные резисторы
- Расчет трех параллельных резисторов онлайн
Параллельное соединение резисторов
Параллельное соединение резисторов характеризуется следующими особенностями входные клеммы каждого из резисторов соединены друг с другом .
Точно так же в конфигурации с параллельным резистором выходные клеммы также соединены друг с другом.
Из-за этого на через все резисторы проходит одинаковое напряжение, т.е. они имеют одинаковое падение напряжения. Это связано с тем, что концы каждого из резисторов подключены к одной и той же точке цепи и, следовательно, имеют одинаковое напряжение.
Однако общий ток, протекающий через резисторы параллельно, равен сумме токов, протекающих через каждый резистор:
Параллельное соединение легко отличить от последовательного . В конфигурации с последовательным резистором выходная клемма одного подключается к входной клемме следующего. У вас есть больше информации о последовательном соединении резисторов в ссылке, которую я вам только что оставил.
Расчет параллельных резисторов: формула
Для расчета эквивалентного сопротивления нескольких параллельно соединенных резисторов , мы должны применить формулу над этими строками.
Во избежание ошибок в расчетах лучше всего разбить формулу на два шага . Сначала мы вычисляем сумму инверсий каждого резистора и, когда у нас есть результат, мы вычисляем его инверсию, чтобы узнать эквивалентное сопротивление.
Решено упражнение на параллельных резисторах
На примере , На следующем рисунке мы собираемся рассчитать эквивалентное сопротивление конфигурации, подобной той, что у нас есть на следующем рисунке:
Первый шаг Рассчитать сумму инверсий каждого резистора. Таким образом, имеем:
- R = (1/20) + (1/30) + (1/30) = 0,116 Ом
Второй шаг Рассчитайте обратную величину сопротивления только что полученного:
- Треб. = 1 / 0,116 = 8,571 Ом
Таким образом, мы можем заменить резисторы на 20, 30 и 30 Ом одним резистором на 8,571 Ом.
Расчет трех параллельных резисторов онлайн
Если мы хотим решить предыдущий пример, но используя наш онлайн-калькулятор трех параллельных резисторов Если вы хотите использовать резистор, вам нужно только ввести значение каждого резистора в соответствующее поле.
 токов можно рассчитать
токов можно рассчитать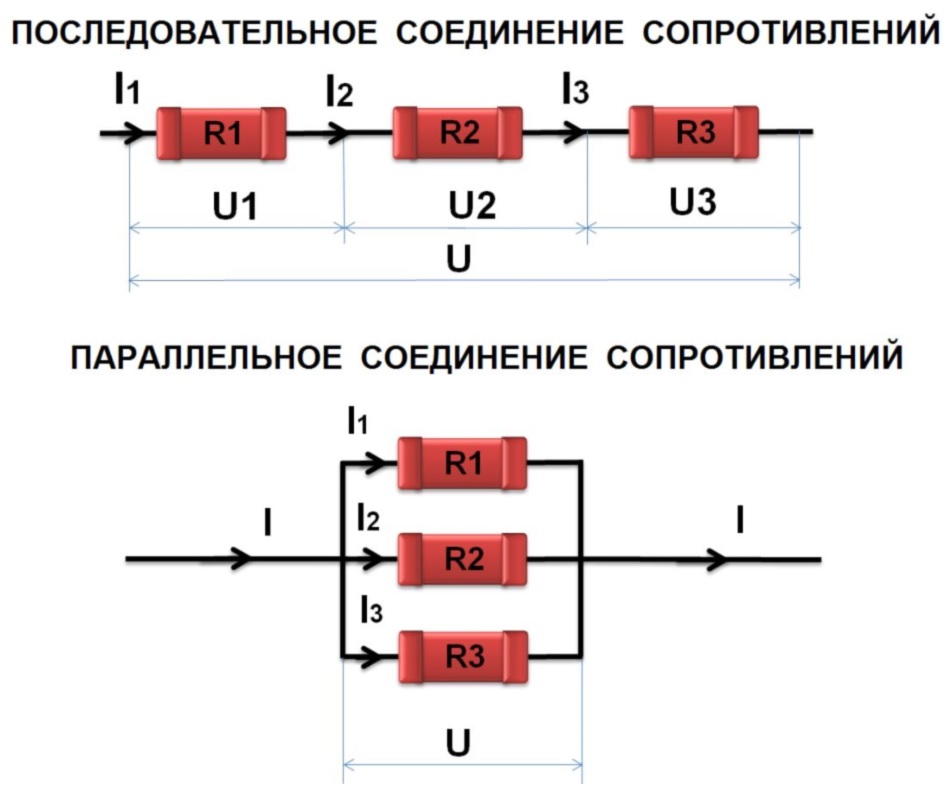 3
3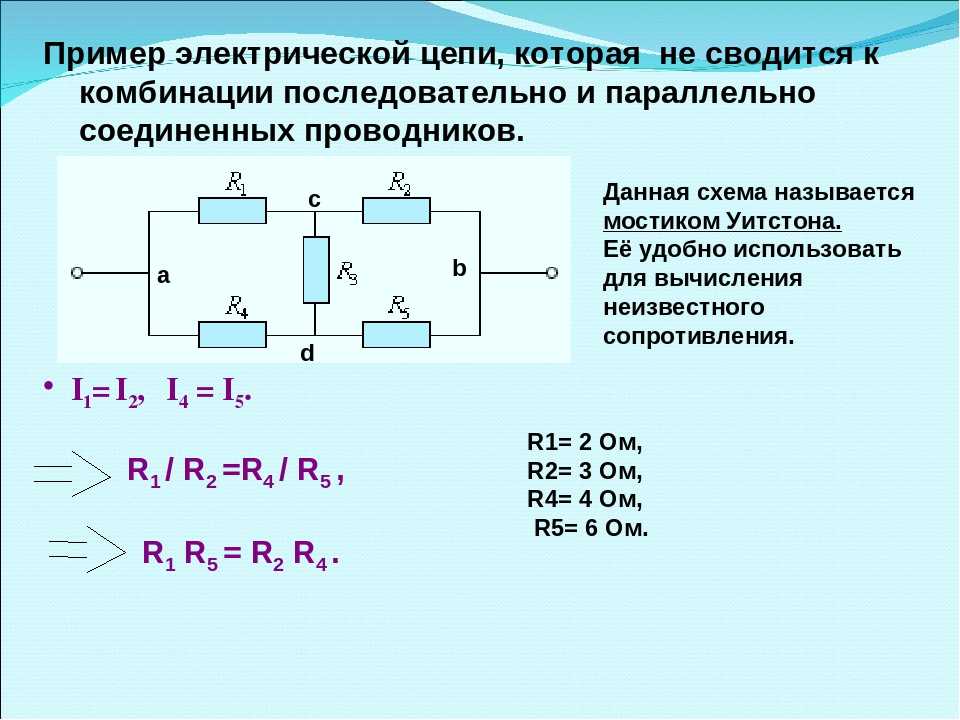 2 1.32
2 1.32 58
58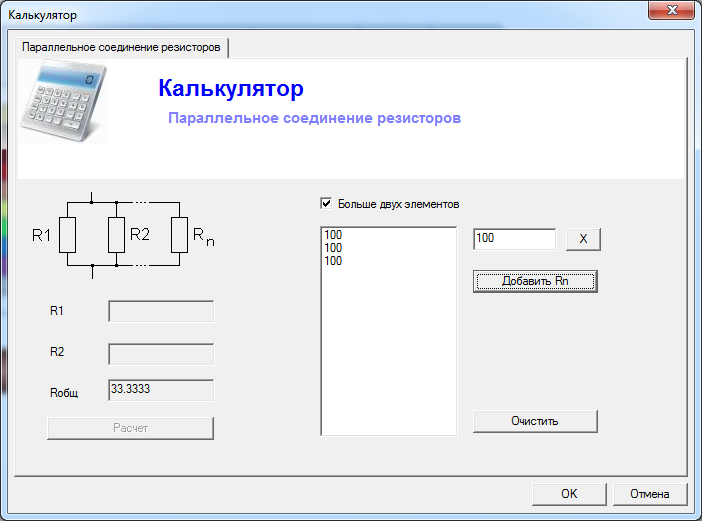 7
7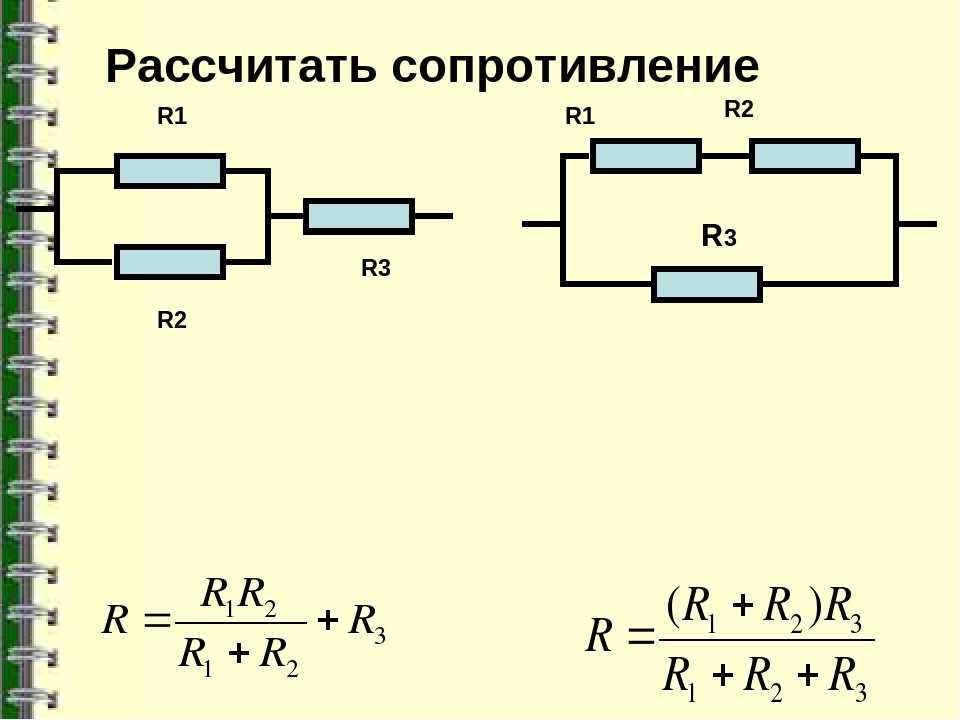 Точно так же в конфигурации с параллельным резистором выходные клеммы также соединены друг с другом.
Точно так же в конфигурации с параллельным резистором выходные клеммы также соединены друг с другом.