Содержание
Как определить емкость конденсатора мультиметром
- Статья
- Видео
Иногда на конденсаторе не указывается его маркировка. Как узнать тогда реальную его емкость, если специального оборудования под рукой нет, а устройство без обозначений? Тогда на помощь приходят различные подручные средства и формулы. Прежде чем приступать к работе, необходимо помнить о том, что конденсатор перед проверкой должен быть разряжен (следует разрядить его контакты). Для этого можно использовать обычную отвертку с изолированной ручкой. Держась за ручку отверткой коснуться контактов, таким образом их замыкая. Далее мы подробно расскажем, как определить емкость конденсатора мультиметром, предоставив инструкцию с видео примером.
- Использование режима «Cx»
- Применение формул
- Другие методики
Использование режима «Cx»
После того, как контакты закоротили, можно осуществлять определение сопротивления. Если элемент исправлен, то сразу после подключения он начнет заряжаться постоянным током. В этом случае сопротивление отобразиться минимальное и будет продолжать расти.
Если элемент исправлен, то сразу после подключения он начнет заряжаться постоянным током. В этом случае сопротивление отобразиться минимальное и будет продолжать расти.
В случае если конденсатор неисправен, то мультиметр будет сразу указывать бесконечность или будет указывать нулевое сопротивление и при этом пищать. Такая проверка осуществляется, если конструкция полярная.
Для того чтобы узнать емкость необходимо иметь мультиметр с функцией измерения параметра «Сх».
Определить емкость с помощью такого мультиметра просто: установить его в режим «Сх» и указать минимальный предел измерения, которым должен обладать данный конденсатор. В таких мультиметрах есть специальные гнезда с определенными пределами измерения. В эти гнезда вставляется конденсатор согласно его пределу измерения и происходит определение его параметров.
Если в тестере таких гнезд нет, то определить емкость можно с помощью измерительных щупов, как показано на фото ниже:
Важно! В отдельной статье мы рассказывали о том, как проверить исправность конденсатора. Рекомендуем также ознакомиться с этим материалом!
Рекомендуем также ознакомиться с этим материалом!
Применение формул
Что делать, если под рукой нет такого мультиметра с гнездами измерения, а есть только обычный бытовой прибор? В таком случае необходимо вспомнить законы физики, которые помогут определить емкость.
Для начала вспомним, что в случае, когда конденсатор заряжается от источника неизменного напряжения через резистор, то существует закономерность, согласно которой напряжение на устройстве будет подходить к напряжению источника и в конечном итоге сравняется с ним.
Но для того чтобы этого не ожидать, можно процесс упростить. Например, за определенное время, которое равняется 3*RC, во время заряжения элемент достигает напряжения 95% примененного к RC цепи. Таким образом, по току и напряжению можно определить константу времени. А правильнее, если знать вольтаж в блоке питания, номинал самого резистора, происходит определение постоянной времени, а затем и емкости устройства.
Например, есть электролитический конденсатор, узнать емкость которого можно по маркировке, где прописывается 6800 мкф 50в. Но что если устройство давно лежало без дела, а по надписи сложно определить его рабочее состояние? В этом случае лучше проверить его емкость, чтобы знать наверняка.
Но что если устройство давно лежало без дела, а по надписи сложно определить его рабочее состояние? В этом случае лучше проверить его емкость, чтобы знать наверняка.
Для этого необходимо выполнить следующее:
- С помощью мультиметра измерить сопротивление резистора в 10 кОм. Например, оно получилось равно 9880 Ом.
- Подключаем блок питания. Мультиметр переводим в режим замера постоянного напряжения. Затем подключаем его к блоку питания (через его выводы). После этого в блоке устанавливается 12 вольт (на мультиметре должна появиться цифра 12,00 В). Если же не удалось отрегулировать напряжение в блоке питание, то тогда записываем те результаты, которые получились.
- С помощью конденсатора и резистора собираем электрическую RC-цепь. На схеме ниже указана простая RC-цепочка:
- Закоротить конденсатор и подключить цепь к питанию. С помощью прибора еще раз определить напряжение, которое подается на цепь, и записать это значение.
- Затем необходимо высчитать 95% от полученного значения.
 К примеру, если это 12 Вольт, то это будет 11,4 В. То есть, за определенное время, которое равняется 3*RC, конденсатор получит напряжение в 11,4 В. Формула выглядит следующим образом:
К примеру, если это 12 Вольт, то это будет 11,4 В. То есть, за определенное время, которое равняется 3*RC, конденсатор получит напряжение в 11,4 В. Формула выглядит следующим образом: - Осталось определить время. Для этого устройство раскорачиваем и с помощью секундомера производим отсчет. Определение 3*RC будет вычисляться таким образом: как только напряжение на устройстве будет равно 11,4 В, то это и будет означать нужное время.
- Производим определение. Для этого полученное время (в секундах) делим на сопротивление в резисторе и на три. Например, получилось 210 секунд. Эту цифру делим на 9880 и на 3. Получилось значение 0,007085. Это величина указывается в фарадах, или 7085 мкф. Допустимое отклонение может быть не более 20%. Если учитывать, что на изделии указано 6800 мкф, наши расчеты подтверждаются и укладываются в норматив.
А как определить емкость керамического конденсатора? В этом случае можно сделать определение с помощью сетевого трансформатора. Для этого RC-цепочку подсоединяем ко вторичной обмотке трансформатора, и его подсоединяют в сеть. Далее с помощью мультиметра осуществляется замер напряжения на конденсаторе и на резисторе. После этого необходимо сделать подсчеты: высчитывается ток, что проходит через резистор, затем его напряжение делится на сопротивление. Получается емкостное сопротивление Хс.
Далее с помощью мультиметра осуществляется замер напряжения на конденсаторе и на резисторе. После этого необходимо сделать подсчеты: высчитывается ток, что проходит через резистор, затем его напряжение делится на сопротивление. Получается емкостное сопротивление Хс.
Если есть частота тока и Хс, можно определить емкость по формуле:
Другие методики
Также емкость можно определить и с помощью баллистического гальванометра. Для этого используется формула:
где:
- Cq — баллистическая постоянная гальванометра;
- U2 — показания вольтметра;
- a2 — угол отклонения гальванометра.
Определение значения методом амперметра вольтметра осуществляется следующим образом: измеряется напряжение и ток в цепи, после чего значение емкости определяется по формуле:
Напряжение при таком методе определения должно быть синусоидальным.
Измерение значения возможно и при помощи мостиковой схемы. В этом случае схема моста переменного тока указывается ниже:
Здесь одно плечо моста образуется за счет элемента, который необходимо измерить (Cx). Следующее плечо состоит из конденсатора без потерь и магазина сопротивлений. Оставшиеся два плеча состоят из магазинов сопротивлений. Подключаем в одну диагональ источник питания, в другую – нулевой индикатор. И рассчитываем значение по формуле:
Следующее плечо состоит из конденсатора без потерь и магазина сопротивлений. Оставшиеся два плеча состоят из магазинов сопротивлений. Подключаем в одну диагональ источник питания, в другую – нулевой индикатор. И рассчитываем значение по формуле:
Напоследок рекомендуем просмотреть полезное видео по теме:
Это все, что мы хотели рассказать вам о том, как определить емкость конденсатора мультиметром. Надеемся, предоставленная информация была для вас полезной и интересной!
Наверняка вы не знаете:
- Как выбрать мультиметр для дома
- Как определить короткое замыкание
- Как проверить работоспособность транзистора
Как определить емкость конденсатора? Емкость конденсаторов: определение, формулы, примеры.
Содержание
С использованием мультиметра и формул
Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.
Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.
Режим «Сх» в мультиметре
Менее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).
Рис. 2. Схема подключения конденсатора
Алгоритм измерения следующий:
- Измерьте напряжение источника питания щупами контактов измерительного прибора.
- Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
- Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
- Замерьте напряжение образованной цепи с помощью мультиметра.
- Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
- Вычислите 95% от полученного значения.
 Запишите показатели измерений.
Запишите показатели измерений. - Возьмите секундомер и включите его одновременно с убиранием закоротки.
- Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
- По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.
Рис. 3. Измерение с помощью тестера. Проверка
Подчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.
Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*Xc , где f– частота тока, а Xc– ёмкостное сопротивление.
Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*Xc , где f– частота тока, а Xc– ёмкостное сопротивление.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Вам это будет интересно Удельное электрическое сопротивление металлических проводников
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
- 1,0006 — воздух;
- 2,5—3,5 — бумага;
- 3—10 — стекло;
- 5—7 — слюда.
Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.
Осциллографом
С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = UR / UC* ( 1 / 2*π*f*R ).
Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = UR / UC* ( 1 / 2*π*f*R ).
Рис. 4. Простая схема
Алгоритм вычисления простой:
- Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
- Измерьте амплитуды напряжений на конденсаторе и на резисторе.
- Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
- Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.
При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r4 / Cx = r2 / C0.
5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r4 / Cx = r2 / C0.
Рисунок 5. Мостовая схема
Плоский конденсатор и его емкость
Плоским конденсатором называют конденсатор, который состоит из двух одинаковых пластин, которые параллельны друг другу. Пластины могут быть разной формы. На практике чаще всего можно встретить квадратные, прямоугольные и круглые пластины. Давайте рассмотрим простой плоский квадратный конденсатор.
Основные расчеты конденсаторов — инженерное мышление
Конденсаторы используются во многих цепях для различных целей, поэтому мы изучим некоторые основные расчеты конденсаторов для цепей постоянного тока.
Прокрутите вниз, чтобы посмотреть обучающее видео на YouTube
Конденсаторы в цепях постоянного тока
Конденсаторы обычно выглядят так. У нас есть конденсатор электролитического и керамического типа. Электролитик поляризован, что означает, что одна сторона должна быть подключена к плюсу, а другая к минусу источника питания. Керамический тип, как правило, может быть подключен любым способом. На стороне электролитического конденсатора мы находим пунктирную линию, указывающую на отрицательную сторону, длинный вывод также указывает на положительную сторону нового конденсатора. Но они обычно обрезаются во время установки, поэтому не полагайтесь только на это. Эти два конденсатора представлены такими символами, обратите внимание, что поляризованный конденсатор имеет небольшой символ плюса, указывающий на положительную сторону.
У нас есть конденсатор электролитического и керамического типа. Электролитик поляризован, что означает, что одна сторона должна быть подключена к плюсу, а другая к минусу источника питания. Керамический тип, как правило, может быть подключен любым способом. На стороне электролитического конденсатора мы находим пунктирную линию, указывающую на отрицательную сторону, длинный вывод также указывает на положительную сторону нового конденсатора. Но они обычно обрезаются во время установки, поэтому не полагайтесь только на это. Эти два конденсатора представлены такими символами, обратите внимание, что поляризованный конденсатор имеет небольшой символ плюса, указывающий на положительную сторону.
При подключении к источнику постоянного тока напряжение батареи будет выталкивать электроны в конденсатор, поэтому конденсатор заряжается до того же напряжения, что и батарея. Конденсаторы заряжаются почти мгновенно при прямом подключении к батарее, но мы почти всегда используем резистор, это задержит время зарядки, и позже в этой статье мы увидим, как это рассчитать.
Внутри конденсатора с одной стороны скопилось много электронов, они не могут двигаться из-за изолирующего материала между двумя сторонами. Поскольку электроны заряжены отрицательно, у нас есть накопление заряда на одной стороне по сравнению с другой, поэтому у нас есть разница в напряжении между двумя выводами.
Эти электроны удерживаются на месте, и конденсатор может удерживать этот заряд в течение длительного периода времени. Когда указан путь, они будут разряжаться, пока не опустеют. Электроны не проходят через конденсатор; они просто накапливаются внутри, а затем высвобождаются.
Количество заряда, накопленного в конденсаторе, рассчитывается по формуле Заряд = емкость (в фарадах), умноженная на напряжение. Итак, для этого конденсатора 12 В 100 мкФ микрофарад мы конвертируем микрофарады в фарады (100/1 000 000 = 0,0001 Ф). Затем умножаем это на 12 В, чтобы увидеть, что он хранит заряд 0,0012 кулонов. 92
= 0,5 x 0,0001F x 144
= 0,0072 Дж
Мы знаем, что конденсатор будет заряжаться до напряжения батареи. Итак, если мы подключим конденсатор таким образом, каково будет напряжение на конденсаторе? Будет 1,5В. Если мы вот так подключим конденсатор, каково будет его напряжение? Тоже будет 1,5В. Это два разных способа соединения конденсаторов в цепях, последовательное или параллельное. Это приведет к тому, что конденсаторы будут работать по-разному.
Итак, если мы подключим конденсатор таким образом, каково будет напряжение на конденсаторе? Будет 1,5В. Если мы вот так подключим конденсатор, каково будет его напряжение? Тоже будет 1,5В. Это два разных способа соединения конденсаторов в цепях, последовательное или параллельное. Это приведет к тому, что конденсаторы будут работать по-разному.
Параллельные конденсаторы
Если мы поставили конденсатор параллельно с лампой, то при извлечении батарейки конденсатор начнет питать лампу, она медленно тускнеет по мере разрядки конденсатора. Если бы мы использовали два конденсатора, мы могли бы питать лампу дольше.
Допустим, конденсатор 1 = 10 мкФ, а конденсатор 2 = 220 мкФ. Как рассчитать общую емкость? Это очень просто, ответ 230 мкФ. Конденсаторы соединены параллельно. Итак, 10 мкФ + 220 мкФ = 230 мкФ. Мы можем продолжать добавлять больше, например, конденсатор на 100 мкФ, и общее количество будет просто суммой всех конденсаторов. Размещая их параллельно, мы, по сути, объединяем их, чтобы сформировать больший конденсатор. Это очень полезно, потому что, если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его нет, мы можем просто использовать конденсаторы меньшего размера, такие как 2x 1000 мкФ или 4x 500 мкФ и т. д. Он также часто используется для фильтрации шума и обеспечения большей емкости. ток в цепях с высоким потреблением.
Это очень полезно, потому что, если, например, нам нужен большой конденсатор на 2000 мкФ, но у нас его нет, мы можем просто использовать конденсаторы меньшего размера, такие как 2x 1000 мкФ или 4x 500 мкФ и т. д. Он также часто используется для фильтрации шума и обеспечения большей емкости. ток в цепях с высоким потреблением.
Общий заряд, хранящийся в параллельных конденсаторах, равен: заряд = общая емкость, умноженная на напряжение. Итак, у нас есть батарея на 9 В и два конденсатора общей емкостью 230 мкФ. Поскольку это параллельно, этот провод 9 В, а этот 0 В, поэтому оба конденсатора заряжены до 9 В. Следовательно, 0,00023 Ф, умноженное на 9 В = 0,00207 кулона. И с тремя конденсаторами мы имеем 330 мкФ (0,00033 Ф), умноженные на 9 В = 0,00297 кулонов.
Мы также можем рассчитать заряд каждого конденсатора в отдельности. Мы просто используем одну и ту же формулу для каждого конденсатора, вы можете увидеть ответы на экране.
Конденсатор 1 = 0,00001 F x 9V = 0,00009 кулоны
Конденсатор 2 = 0,00022 F x 9V = 0,00198 кулоны
3 = 0,0001 F x 9V = 0,0009 Coulombs
. Если мы поместим конденсатор последовательно с лампой, когда мы нажмем переключатель, она загорится, но затем станет тусклее, когда конденсатор достигнет уровня напряжения батареи, и как только он достигнет этого, лампа погаснет. Помните, что электроны не могут проходить через конденсатор из-за изолирующего материала внутри. Электроны просто накапливаются внутри одной пластины и по мере их накопления отбрасывают такое же количество с противоположной пластины. Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея удалена, конденсатор не может разрядиться, поэтому он будет удерживать напряжение на том же уровне. Неважно, подключаем мы аккумулятор или отключаем, лампа не включится. Однако, если мы обеспечим другой путь, то при нажатии переключателя конденсатор теперь может разряжаться, так что электроны могут течь через лампу и освещать ее. Он станет тусклее по мере разрядки конденсатора.
Если мы поместим конденсатор последовательно с лампой, когда мы нажмем переключатель, она загорится, но затем станет тусклее, когда конденсатор достигнет уровня напряжения батареи, и как только он достигнет этого, лампа погаснет. Помните, что электроны не могут проходить через конденсатор из-за изолирующего материала внутри. Электроны просто накапливаются внутри одной пластины и по мере их накопления отбрасывают такое же количество с противоположной пластины. Таким образом, ток может течь только тогда, когда конденсатор заряжается или разряжается. В настоящее время, когда батарея удалена, конденсатор не может разрядиться, поэтому он будет удерживать напряжение на том же уровне. Неважно, подключаем мы аккумулятор или отключаем, лампа не включится. Однако, если мы обеспечим другой путь, то при нажатии переключателя конденсатор теперь может разряжаться, так что электроны могут течь через лампу и освещать ее. Он станет тусклее по мере разрядки конденсатора.
Что, если бы у нас было 2 конденсатора, соединенных последовательно, опять же, конденсатор 1 имеет емкость 10 мкФ, а конденсатор 2 — 220 мкФ. Как найти полную емкость? Для этого мы используем эту формулу, она может показаться сложной, но на самом деле она очень проста. Все, что нам нужно сделать, это ввести значения наших конденсаторов 10 и 220 мкФ. Мы можем ввести это как это на наших калькуляторах или в Excel. Но при ручном вычислении мы делаем 1, деленное на 10, что равно 0,1, и 1, деленное на 220, что равно 0,00454. Мы складываем их вместе, чтобы получить 0,10454, а затем 1, деленное на это, дает в общей сложности 9.0,56 мкФ. Обратите внимание, что общая емкость теперь меньше конденсатора с наименьшим значением.
Как найти полную емкость? Для этого мы используем эту формулу, она может показаться сложной, но на самом деле она очень проста. Все, что нам нужно сделать, это ввести значения наших конденсаторов 10 и 220 мкФ. Мы можем ввести это как это на наших калькуляторах или в Excel. Но при ручном вычислении мы делаем 1, деленное на 10, что равно 0,1, и 1, деленное на 220, что равно 0,00454. Мы складываем их вместе, чтобы получить 0,10454, а затем 1, деленное на это, дает в общей сложности 9.0,56 мкФ. Обратите внимание, что общая емкость теперь меньше конденсатора с наименьшим значением.
Если мы добавили в схему третий конденсатор на 100 мкФ, то получим общую емкость 8,73 мкФ. Значит, уменьшилось еще больше. Это потому, что, объединяя их последовательно, мы существенно увеличиваем толщину изоляционного материала, поэтому притяжение отрицательно заряженных электронов к положительно заряженным отверстиям на противоположной пластине становится слабее.
Общий заряд последовательных конденсаторов находится по формуле: заряд = емкость (в фарадах), умноженная на напряжение.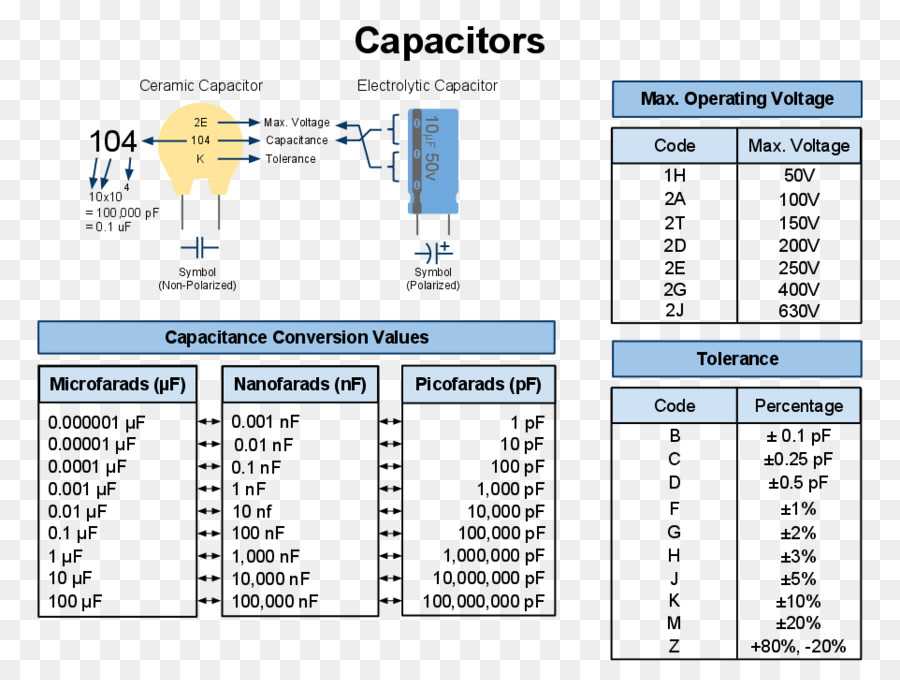 Итак, если мы использовали 9V батареи, мы переводим микрофарады в фарады и видим, что общий заряд равен 0,00008604 кулонов
Итак, если мы использовали 9V батареи, мы переводим микрофарады в фарады и видим, что общий заряд равен 0,00008604 кулонов
(0,00000956F x 9V = 0,00008604 кулонов)
Кулоны)
Заряд, удерживаемый каждым конденсатором в отдельности, очень легко рассчитать в последовательных цепях. Это то же самое, что общее количество. Каждый конденсатор содержит одинаковое количество электронов при последовательном соединении. Это потому, что когда мы заряжали конденсаторы, ток был одинаковым во всех частях цепи. То же самое количество электронов, которые были вытолкнуты в одну пластину, были вытеснены из противоположной пластины, поэтому каждый последовательный конденсатор может быть заряжен только до одного и того же уровня. Таким образом, наименьший конденсатор будет ограничивающим фактором.
Однако, поскольку каждый конденсатор может иметь разную емкость, напряжение каждого конденсатора будет разным. Напряжение каждого конденсатора находим по формуле напряжение = заряд (в кулонах) деленное на емкость (в фарадах).
Итак, для этой схемы мы видим, что конденсатор 1 на 7,8 В, конденсатор 2 на 0,35 В и конденсатор 3 на 0,78 В. Они объединяются в общее напряжение батареи, которое составляет 9 В.
Конденсатор 1: 0,00007857 C / 0,00001 F = 7,857 В
Конденсатор 2: 0,00007857 C / 0,00022 F = 0,357 В
Конденсатор 3: 0,00007857 C / 0,0001 F = 0,786 В
Общее напряжение = 7,857 В + 0,357 В + 0,786 В = 9 В переключатель все последовательно. Конденсатор полностью разряжен, и мы считываем 0 В на двух выводах.
Когда мы замыкаем переключатель, конденсатор заряжается. Напряжение будет увеличиваться до тех пор, пока не сравняется с напряжением батареи. Рост напряжения не мгновенный, он имеет экспоненциальную кривую. Сначала напряжение быстро увеличивается, а затем замедляется, пока не достигнет того же уровня напряжения, что и батарея.
Мы разделили эту кривую на 6 сегментов, но нас интересуют только первые 5, потому что на 5 маркере мы в основном находимся на полном напряжении, поэтому мы можем игнорировать все, что дальше этого. Каждый сегмент представляет нечто, называемое постоянной времени. Следовательно, поскольку у нас есть 5 сегментов, у нас есть 5 постоянных времени, поэтому потребуется 5 постоянных времени, чтобы зарядить конденсатор от 0 до чуть менее 100%. Все, что нам нужно сделать, это вычислить длину одной постоянной времени, а затем умножить ее на 5.
Каждый сегмент представляет нечто, называемое постоянной времени. Следовательно, поскольку у нас есть 5 сегментов, у нас есть 5 постоянных времени, поэтому потребуется 5 постоянных времени, чтобы зарядить конденсатор от 0 до чуть менее 100%. Все, что нам нужно сделать, это вычислить длину одной постоянной времени, а затем умножить ее на 5.
Чтобы вычислить одну постоянную времени, мы используем эту формулу.
Постоянная времени (в секундах) = сопротивление (в Омах), умноженное на емкость (в Фарадах). Итак, мы конвертируем значение нашего резистора в омы, а значение конденсатора в фарады и видим, что 10 000 Ом, умноженные на 0,0001 фарад, равняются 1. Итак, в этом примере постоянная времени равна 1 секунде. Следовательно, 5 из них — это 5 секунд. Это означает, что для полной зарядки этого конденсатора до 9 В требуется 5 секунд.
Если бы сопротивление резистора составляло всего 1000 Ом, постоянная времени была бы равна 0,1 секунды, поэтому для достижения
потребовалось бы 0,5 секунды.
 V. Если бы конденсатор был 1000 микрофарад, это заняло бы всего 50 секунд. Таким образом, с увеличением размера конденсатора время, затрачиваемое на это, увеличивается. Если значение резистора увеличивается, время, необходимое для этого, также увеличивается.
V. Если бы конденсатор был 1000 микрофарад, это заняло бы всего 50 секунд. Таким образом, с увеличением размера конденсатора время, затрачиваемое на это, увеличивается. Если значение резистора увеличивается, время, необходимое для этого, также увеличивается.
Возвращаемся к нашей исходной схеме. Таким образом, мы можем рассчитать уровень напряжения для каждой постоянной времени. В точке 1 напряжение всегда равно 63,2 %, в точке 2 — 86,5 %, в точке 3 — 95 %, в точке 4 — 98,2 % и в точке 5 — 99,3 %.
Итак, в этом примере через 1 секунду напряжение на конденсаторе составляет 5,68 В, через 2 секунды — 7,78 В, через 3 секунды — 8,55 В, через 4 секунды — 8,83 В и через 5 секунд — 8,9 В.4V
Если вам нужен более точный ответ, мы можем рассчитать каждую точку следующим образом.
Точка 1 = 9В-0В)x0,632 = 5,6880В
Точка 2 = ((9В – 5,688В)x0,632)+5,68В = 7,7812В
Точка 3 = ((9В-7,7812В)x0,632 )+7,7812В = 8,5515В
Точка 4 = ((9В-8,55В)x0,632)+8,5515В = 8,8349В
Точка 5 = ((9В-8,8349В)x0,632)+8,8349В = 8,9393В
Помните, что при последовательном соединении ток в цепи уменьшается, а напряжение на конденсаторе увеличивается. При полном напряжении ток в цепи не течет. Если бы резистор был лампой, он мгновенно достиг бы полной яркости, когда переключатель был замкнут, но затем стал бы тусклее, когда конденсатор достиг полного напряжения.
При полном напряжении ток в цепи не течет. Если бы резистор был лампой, он мгновенно достиг бы полной яркости, когда переключатель был замкнут, но затем стал бы тусклее, когда конденсатор достиг полного напряжения.
Время разрядки конденсатора
Когда мы обеспечиваем путь для разрядки конденсатора, электроны покидают конденсатор, и напряжение на конденсаторе уменьшается. Он не разряжается мгновенно, а следует экспоненциальной кривой. Мы разделяем эту кривую на 6 сегментов, но нас интересуют только первые 5. В точке 1 напряжение всегда равно 36,8%, в точке 2 будет 13,5%, в точке 3 будет 5%, в точке 4 будет 1,8% и в точке 5 будет 0,7%.
Например, если бы у нас была батарея на 9 В, лампа с сопротивлением 500 Ом и конденсатор на 2000 мкФ, наша постоянная времени была бы 500 Ом, умноженная на 0,002 фарад, что составляет 1 секунду.
Итак, в тот самый момент, когда батарея отключена, конденсатор будет на 9 В, и, поскольку он питает цепь, лампа также будет. Через 1 постоянную времени, в данном случае 1 секунду, напряжение составит 36,8%, что составляет 3,312 В, через 2 секунды — 1,215 В, через 3 секунды — 0,45 В, через 4 секунды — 0,162 В и через 5 секунд — 0,063 В. Таким образом, лампа будет гореть чуть менее 3 секунд. Явно становится тусклее.
Таким образом, лампа будет гореть чуть менее 3 секунд. Явно становится тусклее.
Как рассчитать последовательно и параллельно конденсаторы – ООО «Китроник»
Параллельные конденсаторы
Когда конденсаторы соединены друг с другом (бок о бок), это называется параллельным соединением. Это показано ниже. Чтобы рассчитать общую общую емкость ряда конденсаторов, соединенных таким образом, необходимо сложить отдельные емкости по следующей формуле: CTotal = C1 + C2 + C3 и т. д. Пример: Рассчитать общую емкость для этих трех конденсаторов, соединенных параллельно. CTotal = C1 + C2 + C3 = 10F + 22F + 47F = 79Ф
Задача 1:
Рассчитайте общую емкость следующих конденсаторов, включенных параллельно.
Конденсаторы серии
Когда конденсаторы соединены один за другим, это называется последовательным соединением. Это показано ниже. Чтобы рассчитать общую общую емкость двух конденсаторов, соединенных таким образом, вы можете использовать следующую формулу:
| Cобщ = | C1 x C2 | и т. д. |
| С1 + С2 |
Пример: Чтобы рассчитать общую емкость для этих двух последовательно соединенных конденсаторов.
Задача 2:
Рассчитайте общую емкость следующих последовательно соединенных конденсаторов.
Три или более последовательно соединенных конденсатора
Для расчета общей общей емкости трех или более конденсаторов, соединенных таким образом, можно использовать следующую формулу: и так далее. Пример: Чтобы рассчитать общую емкость для этих трех последовательно соединенных конденсаторов.
Пример: Чтобы рассчитать общую емкость для этих трех последовательно соединенных конденсаторов.
Задача 3:
Рассчитайте общую емкость следующих последовательно соединенных конденсаторов.
Ответы
Задача 1
1 = 232,2 градуса по Фаренгейту 2 = 169,0 градуса по Фаренгейту 3 = 7,0 градуса по Фаренгейту
Задача 2
1 = 2,48F 2 = 14,99F 3 = 4,11F
Задача 3
1 = 3,33F 2 = 1,167F 3 = 0,35F Примечание Значения конденсаторов в этой рабочей таблице сохранены высокими (близкими к единице или выше). Это делается для упрощения процесса обучения. В действительности типичные номиналы конденсаторов намного меньше единицы. Загрузите pdf-версию этой страницы здесь. Узнайте больше об авторе читать далее » Если вы нашли эту статью полезной и хотите получать от нас обновления продуктов и бесплатные электронные ресурсы, зарегистрируйтесь здесь.
 К примеру, если это 12 Вольт, то это будет 11,4 В. То есть, за определенное время, которое равняется 3*RC, конденсатор получит напряжение в 11,4 В. Формула выглядит следующим образом:
К примеру, если это 12 Вольт, то это будет 11,4 В. То есть, за определенное время, которое равняется 3*RC, конденсатор получит напряжение в 11,4 В. Формула выглядит следующим образом: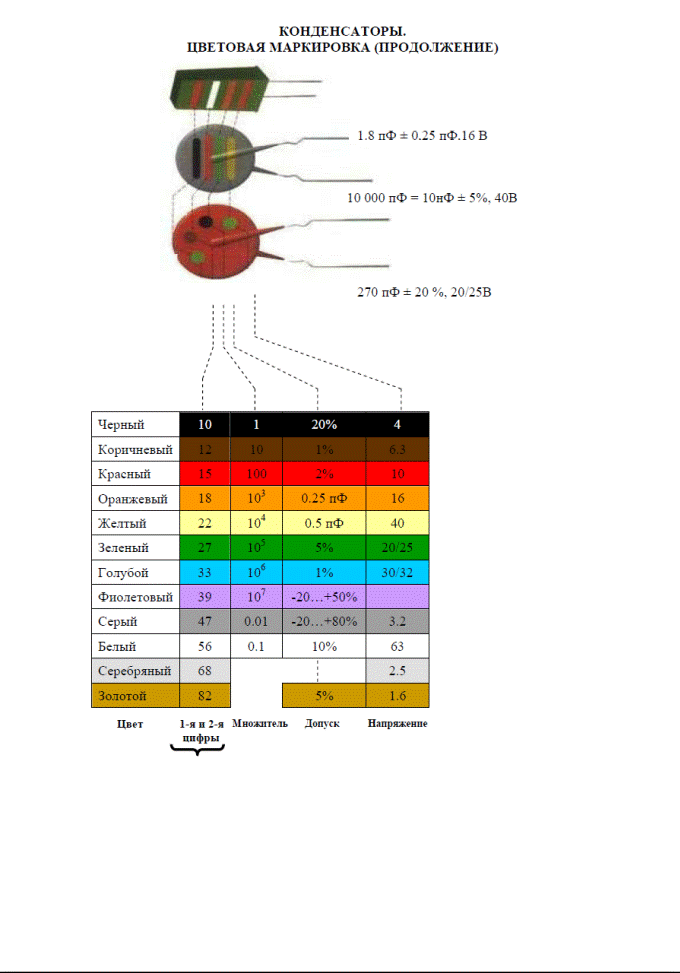 Запишите показатели измерений.
Запишите показатели измерений.