Если проводник замкнут, то есть является контуром, то в нем появляется ток индукции. Явление было открыто в 1831 г. М. Фарадеем. Основной формулой, при помощи которой определяют ЭДС индукции ( где При равномерном изменении магнитного потока основной закон электромагнитной индукции записывают как: ЭДС индукции для контура имеющего N витков, находящегося в переменном магнитном поле можно найти как: где Если прямолинейный проводник движется в однородном магнитном поле, то в нем появляется ЭДС индукции, равная: где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; Разность потенциалов (U) на концах прямого проводника, движущегося в однородном магнитном поле с постоянной скоростью будет равна: где При вращении плоского контура с постоянной скоростью в однородном магнитном поле вокруг оси, которая лежит в плоскости контура в нем появляется ЭДС индукции, которую можно вычислить как: где S – площадь, которую ограничивает виток; Если вращающаяся рамка обладает N витками, при этом самоиндукцией рассматриваемой системы можно пренебречь, то: Если проводник неподвижен в переменном магнитном поле, то ЭДС индукции можно найти как: ru.solverbook.com Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока ( где В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как: Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как: где При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна: где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная: где S – площадь, которую ограничивает виток; Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то: В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле: ru.solverbook.com Сначала напомним, что закон Био-Савара-Лапласа в совокупности с принципом суперпозиции, используют для нахождения вектора магнитной индукции где I – сила тока; В однородном и изотропном магнетике при равных условиях магнитное поле в вакууме ( где Найдем вектор индукции магнитного поля, которое создано прямым тонким проводом, по которому течет ток I (рис.1(a)) для точки, находящейся на расстоянии R от провода в вакууме. При этом концам участка соответствуют углы Силовыми линиями магнитного поля при этом являются окружности, плоскости которых перпендикулярны проводнику, а центры лежат на проводнике. В точке А вектор магнитной индукции направлен перпендикулярно плоскости рис.1 и от нас. В точке А модуль магнитного поля элемента проводника dl, в соответствии с законом Био- Савара – Лапласа запишем как: Принимая во внимание, что Применяя принцип суперпозиции, получим: Напомним теорему о циркуляции в вакууме: В магнитном поле циркуляция вектора магнитной индукции вдоль замкнутого контура L равна сумме токов (с учетом их знаков), которые охватывает контур L: ток в выражении (6) имеет знак плюс, если он связан правилом правого винта с направлением обхода контура. Рассмотрим соленоид бесконечно длинный. Соленоидом называют проводник, намотанный на цилиндр. Пусть ток, текущий по нему равен I, число витков соленоида N, длина соленоида l. Найдем поле внутри соленоида без сердечника ( В качестве кривой, по которой будем рассматривать циркуляцию, используем прямоугольник (рис.2). По теореме о циркуляции для избранного контура имеем: ru.solverbook.com Магнитная индукция определяется способностью влиять на объект с помощью магнитного поля. Эта способность проявляется при перемещении постоянного магнита в катушке, в результате чего в катушке индуцируется (возникает) ток, при этом магнитный поток в катушке также увеличивается. Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся. Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки — именно перемещения), то заряды начинают двигаться под действием этого магнитного поля. В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого. При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля. Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение. Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле. где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника. Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур. Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла. Магнитометры, используемые для ее измерения, называют теслометрами. Единицей измерения магнитной индукции в системе СИ является Тесла (Тл). После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства. pue8.ru Направлением вектора магнитной индукции считают направление, которое показывает северный полюс магнитной стрелки, которая может свободно устанавливаться в магнитном поле. Аналогичное направление имеет положительная нормаль к замкнутому контуру, по которому течет ток. Положительная нормаль имеет направление, совпадающее с направлением перемещения правого винта (буравчика), если его вращают по направлению тока в контуре. При использовании рамки с током или магнитной стрелки можно определить направление вектора Если магнитное поле создает прямой проводник с током, то магнитная стрелка в любой точке этого поля устанавливается по касательной к окружности, плоскость которой перпендикулярна проводнику, центр находится на оси провода. Направление вектора Магнитное поле оказывать действие на каждый участок проводника с током. Используя силу, действующую на проводник с током (силу Ампера), определяют величину вектора магнитной индукции магнитного поля. Так, модуль вектора На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. По величине ее воздействия на заряд также можно установить модуль вектора где Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение: где Данный закон предоставляет нам возможность вычислить вектор магнитной индукции ( где I – сила тока; Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( где Магнитная индукция поля ( В однородном и изотропном веществе циркуляция вектора индукции магнитного поля по любому контуру L равна: где В случае непрерывного распределения тока по поверхности S силу тока вычисляют при помощи выражения: где Примеры частных случаев формул для нахождения вектора магнитной индукции см. раздел «Магнитная индукция формула» ru.solverbook.com Все магниты разделяются между собой по силе своего воздействия. Таким образом, существует определенная величина, которая характеризует степень проявления силы того или иного магнита. Если быть более точными, то данная сила создается не самими магнитами, а их магнитными полями. Само магнитное поле зависит от векторной величины, которая известна, как индукция магнитного поля или просто магнитная индукция. Для определения величины электромагнитной индукции используется формула B=F/(I*l), где магнитная индукция В, представляющая собой модуль вектора, определяется, как отношение модуля силы F, воздействующей на проводник с током, расположенным перпендикулярно с магнитными линиями, к значению силы тока I, имеющейся в проводнике и длине l самого проводника. На электромагнитную индукцию абсолютно не влияют, ни сила тока, ни длина проводника. Она находится в прямой зависимости и связи, только с магнитным полем. Таким образом, при уменьшении силы тока в проводнике, без изменения каких-либо других показателей, происходит уменьшение не индукции, прямо пропорционально связанной с силой тока, а той силы, с которой магнитное поле воздействует на проводник. При этом, значение самой магнитной индукции остается постоянным. Благодаря этим качествам, электромагнитная индукция выступает в роли количественной характеристики магнитного поля. Измерение магнитной индукции производится в теслах, по формуле: 1 Тл=1 Н/(А*м). Физическую зависимость этой величины от различных факторов, можно определить в ходе проведения несложного эксперимента. Необходимо взять весы, где на одной стороне прикрепляется проводник, а на другой стороне расположены гири. Проводник находится в постоянном электромагнитном поле, при этом, его масса и вес гирь имеют одинаковое значение. После уравновешивания весов, по проводнику пропускается электрический ток. Вокруг него происходит образование магнитного поля, определяемое в соответствии с правилом правой руки. В результате, наблюдается взаимодействие полей постоянного магнита и самого проводника. При этом, равновесие весов будет нарушено. Из-за протекания тока, сторона весов с проводником начинает опускаться. Для того, чтобы вычислить силу воздействия поля на этот проводник, нужно уравновесить его с помощью гирь. Сила их тяжести рассчитывается по специальной формуле, и будет равняться силе магнитного поля, воздействующей на проводник с током. Соотношение этой силы с длиной проводника и силой тока является постоянной величиной. Данная количественная характеристика находится в зависимости только от поля и представляет собой ни что иное, как модуль вектора магнитной индукции. Сама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой. Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках. Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей. electric-220.ru Это основной закон, который используют при вычислениях, которые связаны с электромагнитной индукцией. Формула данного закона выглядит следующим образом: где Магнитный поток, который пронизывает контур, может изменяться из-за разных причин, например, перемещения контура, его деформации, изменения самого магнитного поля. Полная производная в формуле закона электромагнитной индукции охватывает весь спектр действия этих причин. Следует учесть, что из конца вектора нормали к контуру обход контура должен проходить против часовой стрелки. Знак минус в законе индукции отражает правило Ленца. В виде (1), закон электромагнитной индукции записывается в международной системе единиц (СИ). Если изменение магнитного потока происходит равномерно, то формулу закона электромагнитной индукции можно записать как: Формулу закона для электромагнитной индукции, если контур состоит из N витков, соединенных последовательно, записывают в виде: где ЭДС индукции в прямом проводнике, имеющем длину l, движущемся в магнитном поле и пересекающем линии магнитной индукции, если скорость его движения ( Разность потенциалов (U), возникающая на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью v равна: где Если в однородном магнитном поле вращается плоский контур со скоростью где S – площадь, которую ограничивает виток; Если в рамке, вращающейся со скоростью в формуле (6) самоиндукцией витков пренебрегли. Пусть проводник находится в покое, при этом изменяется во времени само магнитное поле, тогда ЭДС индукции можно найти как: ru.solverbook.comФормула закона электромагнитной индукции. Индукция формула
Формулы электромагнитной индукции
Основной закон электромагнитной индукции
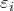 ), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока (
), является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). В соответствии с данным законом, электродвижущая сила индукции в контуре, находящемся в переменном магнитном поле, равна по модулю и противоположна по знаку скорости изменения магнитного потока (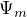 ) через поверхность, которую ограничивает рассматриваемый контур:
) через поверхность, которую ограничивает рассматриваемый контур:![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e1eae4a6f77e7cbc9ffc96b82709c69b_l3.png)
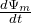 – скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.
– скорость изменения магнитного потока. Полная производная присутствующая в формуле (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) отвечает правилу Ленца. В виде (1) формула ЭДС записана для международной системы единиц (СИ), в других системах вид закона может отличаться.![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{\Delta \Psi_m}{\Delta t} \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-288bfb96f582bb3ff30e040ddbcc0e68_l3.png)
Формулы ЭДС индукции для частных случаев
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\sum^N_{i=1}{\Psi_{mi}}}{dt}=-\frac{d\Psi}{dt} \qquad(3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-16039c391865cbacbbb5cae2b574aa2c_l3.png)
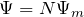 – потокосцепление.
– потокосцепление.![Rendered by QuickLaTeX.com \[\varepsilon_i=-vBl\ \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe7c190915e76d8765b672a69cfda4f1_l3.png)
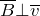 .
. ![Rendered by QuickLaTeX.com \[U=Blv{\sin \alpha } \qquad (5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d5cc596347bb8efe9c510322db48f2e5_l3.png)
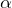 – угол между направлениями векторов
– угол между направлениями векторов 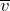 и
и 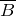 .
.![Rendered by QuickLaTeX.com \[\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)-\frac{d\Psi_{m0}}{dt}} \ \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d87543bdd336d7252fea70898a66873f_l3.png)
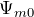 – поток самоиндукции витка;
– поток самоиндукции витка;  — угловая скорость; (
— угловая скорость; (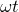 ) – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля
) – угол поворота контура. Необходимо заметить, что формула (5) применима, в случае, если ось вращения составляет прямой угол с направлением вектора внешнего магнитного поля 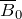 .
.![Rendered by QuickLaTeX.com \[\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)} \ \qquad(7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-003f950e01b3d3ae74ff5dbccf3b38b3_l3.png)
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{\partial \Psi_m}{\partial t} \qquad(8)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0516147d16a90cc7c4ba32c9d1c5e9a5_l3.png)
Примеры решения задач по теме «Электромагнитная индукция»
Формула ЭДС индукции, E
Закон Фарадея – Максвелла для электромагнитной индукции
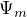 ) через поверхность, которую ограничивает данный контур:
) через поверхность, которую ограничивает данный контур:![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e1eae4a6f77e7cbc9ffc96b82709c69b_l3.png)
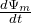 – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
– скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ. ![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{\Delta \Psi_m}{\Delta t} \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-288bfb96f582bb3ff30e040ddbcc0e68_l3.png)
Частные случаи формул ЭДС индукции
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\sum^N_{i=1}{\Psi_{mi}}}{dt}=-\frac{d\Psi}{dt} \qquad(3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-16039c391865cbacbbb5cae2b574aa2c_l3.png)
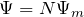 – потокосцепление.
– потокосцепление.![Rendered by QuickLaTeX.com \[\varepsilon_i=-vBl\ \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe7c190915e76d8765b672a69cfda4f1_l3.png)
 .
.![Rendered by QuickLaTeX.com \[\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)-\frac{d\Psi_{m0}}{dt}} \ \qquad(5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-760ba5eb79ef8237be2b26bb112f4148_l3.png)
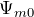 – поток самоиндукции витка;
– поток самоиндукции витка;  — угловая скорость; (
— угловая скорость; (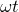 ) – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля
) – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля 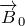 .
.![Rendered by QuickLaTeX.com \[\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)} \ \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3bd369d8d920ecca4891bb66d9bad211_l3.png)
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{\partial \Psi_m}{\partial t} \qquad(7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-70a62239d29a8b580ed7934cf649087a_l3.png)
Примеры решения задач по теме «ЭДС индукции»
Примеры индукции
Пример нахождения формулы для расчета вектора магнитной индукции с применением закона Био-Савара-Лапласа
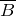 в любой точке поля. Пусть магнитное поле создается в вакууме элементом проводника с током, который можно считать прямолинейным. Для элементарного магнитного поля (
в любой точке поля. Пусть магнитное поле создается в вакууме элементом проводника с током, который можно считать прямолинейным. Для элементарного магнитного поля (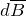 ) закон Био-Савара-Лапласа имеет вид:
) закон Био-Савара-Лапласа имеет вид:![Rendered by QuickLaTeX.com \[d\overline{B}=\frac{{\mu}_0}{4\pi}\frac{I}{r^3}\left[d\overline{l}\overline{r}\right] \qquad (1) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b734f6ae6928d8f01f233c2f2169c161_l3.png)
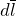 – вектор элемента проводника, равный по модулю длине проводника, совпадающий по направлению с направлением течения тока;
– вектор элемента проводника, равный по модулю длине проводника, совпадающий по направлению с направлением течения тока; 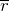 – радиус-вектор, который проводят от элементарного проводника к точке, в которой ищут поле;
– радиус-вектор, который проводят от элементарного проводника к точке, в которой ищут поле; 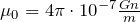 – магнитная постоянная. Вектор
– магнитная постоянная. Вектор 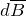 перпендикулярен плоскости, в которой лежат
перпендикулярен плоскости, в которой лежат 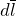 и
и 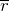 , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта). Силовыми линиями элементарного проводника с током являются окружности, центры которых лежат на проводнике. Для того чтобы получить суммарное поле, которое создает проводник с током используют принцип суперпозиции, который для непрерывного проводника записывается как:
, конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта). Силовыми линиями элементарного проводника с током являются окружности, центры которых лежат на проводнике. Для того чтобы получить суммарное поле, которое создает проводник с током используют принцип суперпозиции, который для непрерывного проводника записывается как:![Rendered by QuickLaTeX.com \[\overline{B}=\int_l{d\overline{B}\ \left(2\right).}\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8e4d8594a21bbb52b9f32900bb543f88_l3.png)
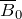 ) связано с магнитным полем в веществе (
) связано с магнитным полем в веществе (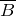 ) как:
) как:![Rendered by QuickLaTeX.com \[\overline{B}=\mu {\overline{B}}_0 \qquad (3) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c3f2d2979c5f3374c01701af2bcdf5e3_l3.png)
 – магнитная проницаемость вещества.
– магнитная проницаемость вещества. 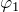 и
и 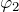 .
.![Rendered by QuickLaTeX.com \[d\overline{B}=\frac{{\mu}_0}{4\pi}\frac{Idl{\sin \alpha}}{r^2} \qquad (4) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e18575d3ade0a016fefaefd7444b1059_l3.png)
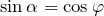 и
и  (см. рис.1 (б)), преобразуем формулу (4).
(см. рис.1 (б)), преобразуем формулу (4).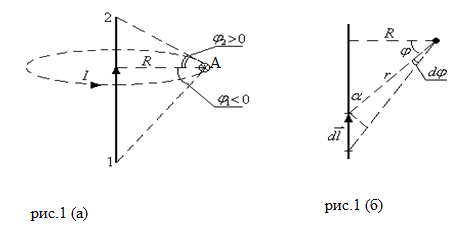
![Rendered by QuickLaTeX.com \[d\overline{B}=\frac{{\mu}_0I}{4\pi R}{\cos \varphi \ d\varphi} \qquad (5) \]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d29a253e3fd8fd2d9babb3c671da9884_l3.png)
![Rendered by QuickLaTeX.com \[B=\int^{{\varphi}_2}_{{\varphi}_1}{\frac{{\mu}_0I}{4\pi R}{\cos \varphi \ d\varphi} =}\frac{{\mu}_0I}{4\pi R}\left({\sin {\varphi}_2} -{\sin {\varphi}_1} \right)=\frac{{\mu}_0I}{4\pi R}({\cos \left({\alpha}_1\right)-{\cos ({\alpha}_2)}} )\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0fb34a6918da7d581e3cd769361fa0ef_l3.png)
Пример использования теоремы о циркуляции для нахождения индукции магнитного поля
![Rendered by QuickLaTeX.com \[\oint_L{\overline{B}d\overline{r}={\mu}_0\sum^N_{m=1}{I_m}} \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ca6a1aac3a69149a556b7fa7cd6e63a2_l3.png)
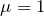 ). Для данного соленоида магнитное поле можно считать однородным. Силовые линии поля при этом имеют направление параллельное оси соленоида. Направление силы тока и
). Для данного соленоида магнитное поле можно считать однородным. Силовые линии поля при этом имеют направление параллельное оси соленоида. Направление силы тока и 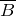 связывает правило правого винта.
связывает правило правого винта. 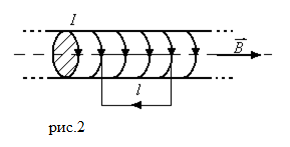
![Rendered by QuickLaTeX.com \[\oint_L{\overline{B}d\overline{r}=Bl={\mu}_0NI\ \to B={\mu}_0\frac{N}{l}}I\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-255ebbb5952d900c8ced098e71aa4165_l3.png)
Примеры решения задач
Магнитная индукция, магнитный поток: определение, формулы, смысл
 Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.
Магнитная индукция (обозначается символом В) – главная характеристика магнитного поля (векторная величина ), которая определяет силу воздействия на перемещающийся электрический заряд (ток) в магнитном поле, направленной в перпендикулярном направлении скорости движения.Физический смысл магнитной индукции
Формула магнитной индукции



Магнитный поток

Формула вектора магнитной индукции
Направление вектора магнитной индукции
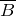 в любой точке магнитного поля.
в любой точке магнитного поля. 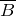 определяют при помощи правила правого винта (правила буравчика), которое говорит о том, что если поступательное перемещение буравчика совпадает с направлением течения тока в проводнике, то вращение головки винта совпадает с направлением вектора магнитной индукции.
определяют при помощи правила правого винта (правила буравчика), которое говорит о том, что если поступательное перемещение буравчика совпадает с направлением течения тока в проводнике, то вращение головки винта совпадает с направлением вектора магнитной индукции. Величина (модуль) вектора магнитной индукции
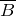 равен частному от деления максимальной силы Ампера
равен частному от деления максимальной силы Ампера 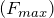 , с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника
, с которой магнитное поле оказывает воздействие на отрезок проводника с током (I) к произведению силы тока на длину проводника 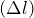 :
:![Rendered by QuickLaTeX.com \[B=\frac{F_{max}}{I\Delta l} \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9eafc6973f1add0a3abc9276019cf559_l3.png)
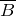 :
:![Rendered by QuickLaTeX.com \[B=\frac{F_L}{qv{\sin \alpha \ } } \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e37200a5647a761779fbee63c3d16897_l3.png)
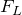 – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле;
– модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; 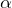 – это угол между векторами
– это угол между векторами 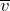 и
и 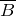 . Направления
. Направления 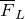 , векторов
, векторов 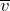 и
и 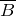 связаны между собой правилом левой руки.
связаны между собой правилом левой руки.![Rendered by QuickLaTeX.com \[B=\frac{M_{max}}{p_m} \qquad(3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-6072126f6fd4bfe8e0a4889242934cac_l3.png)
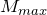 – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом
– максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом 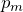 , равным единице, если нормаль к рамке перпендикулярна направлению поля.
, равным единице, если нормаль к рамке перпендикулярна направлению поля.Основные формулы, которые служат для вычисления вектора магнитной индукции
Закон Био-Савара-Лапласа
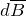 ) в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:
) в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:![Rendered by QuickLaTeX.com \[d\overline{B}=\frac{{\mu }_0}{4\pi }\frac{I}{r^3}\left[d\overline{l}\overline{r}\right]\ \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-9610a70becbb4659864e801ec8db4901_l3.png)
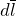 – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока;
– вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; 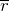 – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле;
– радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; 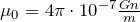 – магнитная постоянная. Вектор
– магнитная постоянная. Вектор 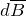 является перпендикулярным к плоскости, в которой расположены
является перпендикулярным к плоскости, в которой расположены 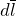 и
и 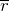 , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
, конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта). 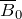 ) и в веществе (
) и в веществе (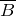 ), при одинаковых условиях, связывает формула:
), при одинаковых условиях, связывает формула:![Rendered by QuickLaTeX.com \[\overline{B}=\mu {\overline{B}}_0\ \qquad(5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-b7f5728be79a0b3c6416ef3e9cd017ff_l3.png)
 – относительная магнитная проницаемость вещества.
– относительная магнитная проницаемость вещества. Принцип суперпозиции
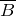 ), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей (
), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей (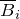 ):
):![Rendered by QuickLaTeX.com \[\overline{B}=\sum^N_{i=1}{{\overline{B}}_i}\ \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f451f154356638ca271a1bcb15059d17_l3.png)
Теорема о циркуляции
![Rendered by QuickLaTeX.com \[\oint_L{\overline{B}d\overline{l}=\mu {\mu }_0\sum^N_{k=1}{I_k}} \qquad (7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-1872d56fa88e9d0876c1116e8b684e63_l3.png)
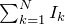 – сумма токов проводимости с учетом их знака, которые охвачены рассматриваемым контуром;
– сумма токов проводимости с учетом их знака, которые охвачены рассматриваемым контуром;  – магнитная проницаемость вещества. В том случае, если направление обхода контура связано с направлением течения тока при помощи правила правого винта, то ток считают положительным.
– магнитная проницаемость вещества. В том случае, если направление обхода контура связано с направлением течения тока при помощи правила правого винта, то ток считают положительным. ![Rendered by QuickLaTeX.com \[I=\int_S{\overline{j}d\overline{S}} \qquad (8)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-2f2a7ff0ba64b322d0210c0ae8221397_l3.png)
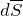 равен по модулю площади элемента поверхности
равен по модулю площади элемента поверхности 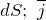 – плотность тока.
– плотность тока.Примеры решения задач по теме «Вектор магнитной индукции»
Индукция магнитного поля
Формула
Зависимость магнитной индукции
Линии магнитной индукции
Формула закона электромагнитной индукции
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\Psi_m}{dt} \qquad(1)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-e1eae4a6f77e7cbc9ffc96b82709c69b_l3.png)
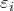 – электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции.
– электродвижущая сила (ЭДС) индукции, которая возникает в проводнике, если он находится в переменном магнитном поле. Если проводящим телом является, например, замкнутый контур, то в нем течет электрический ток, который называют током индукции. 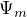 – магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность.
– магнитный поток, через поверхность, ограниченную этим контуром. Формула (1) означает то, что ЭДС индукции равна по модулю и противоположна по знаку скорости изменения магнитного потока через некоторую поверхность. ![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{\Delta \Psi_m}{\Delta t} \qquad(2)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-288bfb96f582bb3ff30e040ddbcc0e68_l3.png)
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{d\sum^N_{i=1}{\Psi_{mi}}}{dt}=-\frac{d\Psi}{dt} \qquad(3)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-16039c391865cbacbbb5cae2b574aa2c_l3.png)
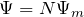 – потокосцепление.
– потокосцепление.Результаты применения основного закона электромагнитной индукции
Формулы ЭДС индукции для частных случаев
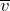 ) перпендикулярна вектору магнитной индукции (
) перпендикулярна вектору магнитной индукции (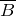 ), равна:
), равна:![Rendered by QuickLaTeX.com \[\varepsilon_i=-vBl\ \qquad(4)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-fe7c190915e76d8765b672a69cfda4f1_l3.png)
![Rendered by QuickLaTeX.com \[U=Blv{\sin \alpha } \qquad (5)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d5cc596347bb8efe9c510322db48f2e5_l3.png)
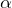 – угол между направлением вектора скорости и направлением вектора магнитной индукции.
– угол между направлением вектора скорости и направлением вектора магнитной индукции. , при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора
, при этом ось вращения находится в плоскости витка и составляет угол в 900 с направлением вектора 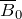 внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:
внешнего магнитного поля, то в контуре появляется ЭДС индукции равная:![Rendered by QuickLaTeX.com \[\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)-\frac{d\Psi_{m0}}{dt}} \ \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d87543bdd336d7252fea70898a66873f_l3.png)
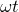 – мгновенное значение угла между
– мгновенное значение угла между 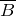 и вектором нормали к плоскости рамки;
и вектором нормали к плоскости рамки; 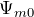 – поток самоиндукции витка.
– поток самоиндукции витка. в однородном магнитном поле, имеется N витков, то
в однородном магнитном поле, имеется N витков, то ![Rendered by QuickLaTeX.com \[\varepsilon_i=B_0S\omega {\sin \left(\omega t\right)} \ \qquad(6)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-3bd369d8d920ecca4891bb66d9bad211_l3.png)
![Rendered by QuickLaTeX.com \[\varepsilon_i=-\frac{\partial \Psi_m}{\partial t} \qquad(7)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-70a62239d29a8b580ed7934cf649087a_l3.png)
Примеры решения задач по теме «Закон электромагнитной индукции»
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''













Поделиться с друзьями: