Резисторы применяются практически во всех электросхемах. Это наиболее простой компонент, в основном, служащий для ограничения или регулирования тока, благодаря наличию сопротивления при его протекании. Резисторы Внутреннее устройство детали может быть различным, но преимущественно это изолятор цилиндрической формы, с нанесённым на его внешнюю поверхность слоем либо несколькими витками тонкой проволоки, проводящими ток и рассчитанными на заданное значение сопротивления, измеряемое в омах. Существующие разновидности резисторов: Важно! Материалом для изготовления практически всех нелинейных деталей, кроме угольных варисторов, применяемых в стабилизаторах напряжения, являются полупроводники. Важно! Импортные резисторные элементы идентичной мощности имеют несколько меньшие размеры, так как российские производятся с некоторым запасом по этому показателю. На схеме мощность показана следующим образом. Условное обозначение мощности Цветовая маркировка резисторов Для расчета сопротивления резистора формула применяемая в первую очередь – это закон Ома: I = U/R. Исходя из этой формулы, можно вывести выражение для сопротивления: R = U/I, где U – разность потенциалов на выводных контактах резистора. Пример. Необходимо провести зарядку аккумулятора 2,4 В зарядным током 50 мА от автомобильной 12-вольтовой батареи. Прямое соединение сделать нельзя из-за слишком высоких показателей по току и напряжению. Но возможно поставить в схему сопротивление, которое обеспечит нужные параметры. Предварительно нужно рассчитать резистор: U = 12-2,4 = 9,6 B Теперь можно уже подобрать нужный резистор по одному показателю. Если рассчитанной детали не нашлось, можно применить соединение из нескольких резисторных элементов, установив их последовательно или параллельно. Расчет сопротивлений при этом имеет свои особенности. Последовательно соединенные сопротивления складываются: R = R1+ R2. Если нужно получить общий результат 200 Ом, и имеется один резистор на 120 Ом, то расчет другого: R2 = R-R1 = 200-120 = 80 Ом. Последовательное соединение При параллельной схеме другая зависимость: 1/R = 1/R1 + 1/R2. Или преобразованный вариант: R = (R1 x R2)/ (R1 + R2). Важно! Параллельное соединение можно использовать, когда в наличии детали с большим сопротивлением, чем требуется, последовательное наоборот. Пример. Необходимо сопротивление 200 Ом. Имеется деталь R2 на 360 Ом. Какое сопротивление подобрать еще? R1 = R2/(R2/R-1) = 360/(360/200-1) = 450 Ом. Параллельное соединение В смешанных схемах присутствуют последовательно-параллельные комбинации. Расчет таких схем сводится к их упрощению путем преобразований. На рисунке ниже представлено, как упростить схему, рассчитывая общий показатель для шести резисторов с учетом их соединения. Расчет сопротивления в смешанной схеме Определив сопротивление, еще нельзя выбрать деталь. Чтобы обеспечить надежную работу схемы, необходимо найти и другой параметр – мощность. Для этого надо знать, как рассчитать мощность резисторного элемента. Формулы, по которым можно рассчитать мощность резистора: Пример. I = 50 мА; R = 200 Ом. Тогда P = I² x R = 0,05² x 200 = 0,5 Вт. Если не учитывать значение тока, расчет мощности резистора ведется по другой формуле. Пример. U = 9,6 В, R = 200 Ом. P = U²/R = 9,6²/200 = 0,46 Вт. Получился тот же результат. Теперь, зная точные параметры рассчитываемого резисторного элемента, подберем радиодеталь. Важно! При выборе деталей возможно их заменить на резисторы с мощностью, больше рассчитанной, но обратный вариант не подходит. Это основные формулы для расчета резисторных деталей, на основании которых производится анализ узлов схемы, где главным является определение токов и напряжений, протекающих через конкретный элемент. elquanta.ru Коэффициент сопротивления дает возможность учитывать потери энергии при движении тела. Чаще всего рассматривают два типа движения: движение по поверхности и движение в веществе (жидкости или газе). Если рассматривают движение по опоре, то обычно говорят о коэффициенте трения. В том случае, если рассматривают движение тела в жидкости или газе, то имеют в виду коэффициент сопротивления формы. Речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем). Данный коэффициент, имеет размерность длины. Основной его единицей в системе СИ будет метр. Иногда, если рассматривают движение вытянутого тела, то считают: где V — объем тела. Рассматриваемый коэффициент сопротивления является безразмерной величиной. Он не учитывает эффектов на поверхности тел, поэтому формула (3) может стать не пригодна, если рассматривается вещество, которое имеет большую вязкость. Коэффициент сопротивления (C) является постоянной величиной пока число Рейнольдса (Re) является неизменным. В общем случае Если тело имеет острые ребра, то эмпирически получено, что для таких тел коэффициент сопротивления остается постоянным в широкой области чисел Рейнольдса. Так опытным путем получено, что для круглых пластинок поставленных поперек воздушного потока, при Сопротивление шаров было исследовано для широкой области чисел Рейнольдса до При В справочниках представлены коэффициенты сопротивления для круглых цилиндров, шаров и круглых пластинок в зависимости от числа Рейнольдса. В авиационной технике задача о нахождении формы тела с минимальным сопротивлением имеет особое значение. ru.solverbook.com Существует множество методик и практических способов, чтобы определить внутреннее сопротивление источников питания, на постоянном или на переменном токе. В данной статье рассмотрены несложные приёмы измерений и расчётов, когда из всей аппаратуры в наличии имеется только простейший китайский тестер. По описанным в руководствах методикам, производятся измерения и вычисления, результаты которых записываются с точностью до второго знака после запятой. Искомый параметр зависит от типа и величины нагрузки, текущей температуры и состава электролита, степени разряда батарейки и заряженности аккумулятора, и от множества других факторов. Поэтому, всегда будет присутствовать определённая, большая или маленькая, ошибка измерений. Формула для упрощённого расчёта внутреннего электрического сопротивления: Rвн = (R * (Е – U)) / U [1] Е – напряжение без нагрузки. ЭДС покоя – примерно равняется напряжению Е (при высоком входном сопротивлении присоединённого вольтметра), когда химический источник электропитания находился без нагрузки достаточно длительное время (более 2-3 часов). U – кратковременно (не более 10 секунд), под нагрузкой сопротивлением R (2—12 Ом),с номинальной мощностью рассеяния от 2 Вт. Лампочка накаливания для этого не годится, т.к. при нагревании спирали накала, её электросопротивление значительно меняется, существенно увеличивается. Для этих целей хорошо подходит толстая нихромовая (температурный коэффициент сопротивления нихрома – в несколько десятков раз меньше, чем у стали, меди и вольфрама) проволока от старой открытой электроплиты, откалиброванная отдельными отрезками по нужным номиналам R и закреплённая на негорючем диэлектрическом основании. Формула для более точных измерений с двумя различными резисторами (обеспечивающими приблизительно, 20-30 и 70 процентов от допустимого, например, 3 и 9 Ом), то есть, только под нагрузкой: Rвн = (R1 * R2 *(U2 – U1)) / (U1*R2 – U2*R1) [2] Если считать и по току, то могут получаться неточные величины импеданса, с погрешностью. И причина не в том, только лишь, что формулы неправильные, а в том, что внутр. сопротивление тестера ненулевое. При измерениях электрического тока (на верхнем, амперном пределе), с использованием обычных китайских мультиметров – возможна существенная систематическая ошибка из-за внутреннего сопротивления самого прибора. Поэтому, стандартные формулы со значением тока в уравнении – обеспечат максимально точный результат, только тогда, когда применяются с промышленной, специальной аппаратурой, при строгом соблюдении правил и методик лабораторных измерений по ГОСТ (заданные интервалы времени, порядок и последовательность стендовых испытаний). По результатам измерений с двумя резисторами, вычисляется дельта (разница) напряжений и токов: Rвн = dU/dI [3] На практике, применяют и упрощённый способ с одним резистором, где дельта считается от напряжения без нагрузки (как в первом варианте), а ток вычисляется по закону Ома. Как первая формула: Rвн = (Е – U) / (U/R) [4]=[1] Или вариант с реальным измерением тока: (Е – U) / I [5] Так же, зная ток при двух различных нагрузках, математически рассчитывается ток короткого замыкания (теоретически возможный) – по формуле из задачи с уравнениями для школьного курса физики старших классов. Данная формула не учитывает всех химических процессов в элементах электропитания, на предельных нагрузках, и конструктивных особенностей. Поэтому, вычисленное значение будет отличаться от фактически возможного: Iкз = (I1*I2*(R2 – R1)) / (I2*R2 – I1R1) при R1 < R2 При непосредственном измерении Iкз ("коротыша") тестером, тоже, получатся заниженные показатели – из-за внутреннего сопротивления самого прибора. // Быстрый и объективный способ проверки работоспособности – стрелочным тестером, имеющим автоматическую защиту от перегрузки, тестируется аккумулятор или обычная батарейка на "ток короткого замыкания", включая на 2—3 секунды. Должно быть не меньше 2 ампер. Норма – если будет больше 3 А. Метод суровый, но объективный. При таком тестировании – сразу видно "переходную характеристику" во время разряда (по стрелочному индикатору тестера), насколько хорошо аккумулятор держит большую нагрузку. Цифровые показатели – максимальный ток (для вычислений, в качестве Iкз - это не годится, т.к общее сопротивление цепи - ненулевое) и скорость спада. Чтобы не испортить, какой-нибудь, особо ценный элемент питания, в цепь последовательно подключается достаточно мощное (больше 2 Вт) нагрузочное сопротивление, до нескольких сотен миллиом. Если электросопротивление самодельной низкоомной нагрузки измеряется цифровым тестером, на малом пределе (200), то нужно учитывать внутреннее сопротивление самого мультиметра, проводов и контактов. Цифры на табло, при замкнутых накоротко щупах прибора, могут иметь значения, например – 00.3 или 004 Ом, то есть – 300миллиом или 400 миллиом, соответственно, которые нужно будет вычитать. Это уменьшит ошибку измерений, но в конечном результате останется ещё внутренняя погрешность тестера (указывается в тех.паспорте устройства). Поэтому, низкоомные резисторы – лучше мерить по схеме резистивного делителя, на основе точного измерения падения напряжения (в приборе наивысшая точность – именно для DCV) на участке последовательной цепи с эталонным прецизионным резистором (образцовое высокоточное постоянное электросопротивление с точностью 0.05—1%, имеющее на корпусе серую полоску цветной маркировки). Из пропорции Rx/Rэталон=Ux/Uэталон считается искомое электрическое сопротивление Rx. Узнать внутреннее сопротивление любого мультиметра, включённого в режиме омметра, можно с помощью низкоомного прецизионного резистора. Померенное значение R будет отличаться от номинала на искомую величину. Примерные величины внутреннего сопротивления (току) для исправных источников питания повышенной ёмкости, при нормальной температуре:- литиевые элементы – < 200 миллиом.- заряженный свинцовый аккумулятор – первые десятки мОм.- щелочные батарейки (размер АА) – до 200 мОм.- никель-металл-гидридные аккумуляторы (АА, NiMH) – до 150 мОм. Подробнее читайте на Интернет-странице сайта:http://www.kakras.ru/mobile/book/Batteries-and-Accumulators.html#battery-internal-resistanceОпубликовано: 15 апреля 2016 года kakras.livejournal.com Цепи переменного тока часто содержат как емкостные, так и индуктивные сопротивления. Их сложение подчиняется определенным правилам. Если то Реактивное сопротивление индуктивности и конденсатора при последовательном соединении L и С \[ X = X_{L} - X_{C} = ωL - \frac{1}{ωC} \] \[ U = U_{L} - U_{C} = IX_{L} - IX_{C} = IX \] Реактивное сопротивление индуктивности и конденсатора при параллельном соединении L и С \[ B = B_{C} - B_{L} = \frac{1}{X_{C}} - \frac{1}{X_{L}} = ωC - \frac{1}{ωL} \] \[ X = \frac{ωL}{ω^{2}LC-1} \] \[ I = I_{C} - I_{L} = \frac{U}{X_{C}} - \frac{U}{X_{L}} = \frac{U}{X} = UB \] www.fxyz.ru В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные. Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности. Введем понятие полного сопротивления цепи переменному току - Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь. Рисунок 1. Классификация цепей переменного тока. Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи. Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление. В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°. Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) - схема цепи; б) - сдвиг фаз тока и напряжения; в) - треугольник напряжений; д) - треугольник сопротивлений. Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника. Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов. По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление. Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е. Извлекая квадратный корень из обеих частей этого равенства, получим, Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе. Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°. В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи. Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) - схема цепи; б) - треугольник сопротивлений. Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его. Для данного случая: В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи. Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) - схема цепи; б) - треугольник сопротивлений. Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е. Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает). После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е. Или Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б. Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления. Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками. Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) - параллельное соединение R и L; б) - параллельное соединение R и C. Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е. Приводя к общему знаменателю подкоренное выражение, получим: откуда: Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а. Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению. Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно: Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений. В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7). Рисунок 6. Эквивалентная схема колебательного контура. Формула полного сопротивления для этого случая будет: Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде: В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие При соблюдении этого условия полное сопротивление колебательного контура будет равно: где L—индуктивность катушки в Гн; С—емкость конденсатора в Ф; R—активное сопротивление катушки в Ом. ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! www.sxemotehnika.ruФормула сопротивления резистора. Формулы сопротивления
Какой формулой рассчитать мощность резисторов
Виды резисторов
Параметры резисторного элемента
Расчет резисторов
Последовательное соединение
Параллельное соединение
Смешанное соединение
Мощность
Видео
Оцените статью: Коэффициент сопротивления, формула и примеры
Определение коэффициента сопротивления (трения) скольжения
Определение коэффициент сопротивления (трения) качения
Определение коэффициента сопротивления формы
![Rendered by QuickLaTeX.com \[S=V^{\frac{2}{3}}\left(4\right),\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f85afbb652ad732081ed14035cdea9bc_l3.png)
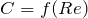 .
. 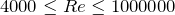 значения коэффициента сопротивления находятся в пределах от 1,1 до 1,12. При уменьшении числа Рейнольдса (
значения коэффициента сопротивления находятся в пределах от 1,1 до 1,12. При уменьшении числа Рейнольдса (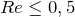 ) закон сопротивления переходит в закон Стокса, который для круглых пластинок имеет вид:
) закон сопротивления переходит в закон Стокса, который для круглых пластинок имеет вид:![Rendered by QuickLaTeX.com \[C=\frac{20,4}{Re}\left(5\right)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-c35a8e38b0d61dfff0a530cc334fdf97_l3.png)
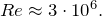 Для
Для 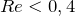 получили:
получили:![Rendered by QuickLaTeX.com \[C=\frac{24}{Re}\left(6\right)\]](/800/600/http/ru.solverbook.com/wp-content/ql-cache/quicklatex.com-5a325e4eb1c3f604d932109524e9abf0_l3.png)
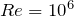 ,
, 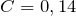 .
.Примеры решения задач
Формулы внутреннего сопротивления - kakras
Определение внутреннего омического сопротивления (постоянному току) у батарейки или аккумулятораРеактивное сопротивление | Формулы и расчеты онлайн
U полное напряжение (эффективное значение), Вольт UC напряжение на емкостном сопротивлении, Вольт UL напряжение на индуктивном сопротивлении, Вольт I полный ток (эффективное значение), Ампер IC ток через емкостное сопротивление, Ампер IL ток через индуктивное сопротивление, Ампер XC емкостное сопротивление, Ом XL индуктивное сопротивление, Ом X полное реактивное сопротивление, Ом B = 1/Х реактивная проводимость, сименс Реактивное сопротивление индуктивности и конденсатора при последовательном соединении L и С
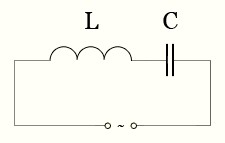
Определить, найти реактивное сопротивление индуктивности и конденсатора при последовательном соединении
Реактивное сопротивление индуктивности и конденсатора при параллельном соединении L и С
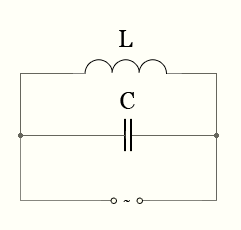
Определить, найти реактивное сопротивление индуктивности и конденсатора при параллельном соединении
В помощь студенту
Реактивное сопротивление
стр. 688
Полное сопротивление цепи переменного тока

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.


 (1)
(1) (2)
(2)
 (3)
(3)
 (4)
(4) (5)
(5) (6)
(6)Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

 (7)
(7) (8)
(8) (9)
(9) (10)
(10)
 (11)
(11) (12)
(12) (13)
(13) (14)
(14)Похожие материалы:
Добавить комментарий
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: