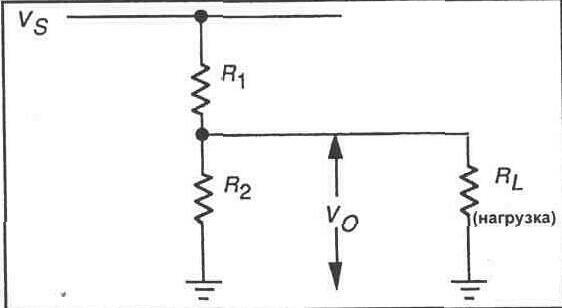
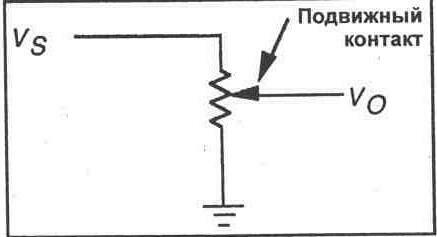
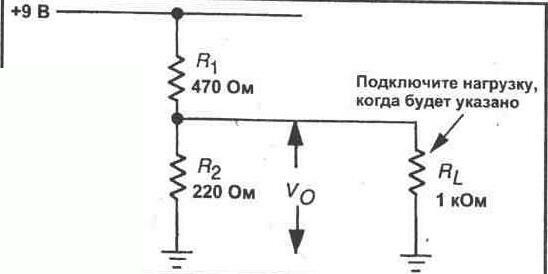
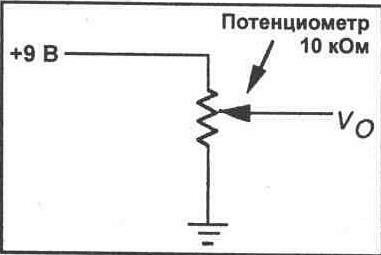
Схема делителя напряжения является простой, но в тоже время фундаментальной электросхемой, которая очень часто используется в электронике. Принцип работы ее прост: на входе подается более высокое входное напряжение и затем оно преобразуется в более низкое выходное напряжение с помощью пары резисторов. Формула расчета выходного напряжения основана на законе Ома и приведена ниже. где: В калькулятор ниже введите любые три известных значения Uвх., Uвых. и R1 и нажмите «Рассчитать», чтобы найти значение R2. Существует несколько обобщений, которые следует учитывать при использовании делителей напряжения. Это упрощения, которые упрощают оценку схемы деления напряжения. Во-первых, если R2 и R1 равны, то выходное напряжение вдвое меньше входного напряжения. Это верно независимо от значений резисторов. Итак, если R1 = R2, то получаем следующее уравнение: Во-вторых, если R2 на порядок больше чем R1, то выходное напряжение Uвых будет очень близко к Uвх., то есть Uвх. ≈ Uвых. А на R1 будет очень мало напряжения. Во-третьих, если наоборот R1 на порядок больше чем R2, то Uвых будет очень маленьким по сравнению с Uвх, то есть будет стремиться к нулю. Практически все входное напряжение упадет в таком случае на R1. Выход Выходное напряжение (Vвых.) www.asutpp.ru ЭКСПЕРИМЕНТ 7 Делители напряжения Цели После проведения данного эксперимента Вы сможете рассчитать выходное напряжение делителя напряжения с нагрузкой и без таковой, а также продемонстрировать, что потенциометр является варьируемым делителем напряжения. Необходимые принадлежности * Цифровой мультиметр * Макетная панель * Источник постоянного напряжения * Один потенциометр 10 кОм * Резисторы — 1/4 Вт, 5%: один резистор 220 Ом, один резистор 470 Ом, один резистор 1 к0м, один резистор 2, 2 к0м, один резистор 3, 3 к0м, один резистор 10 к0м, один резистор 100 к0м. ВВОДНАЯ ЧАСТЬ Делитель напряжения — это резистивная схема, выходное напряжение которой меньше, чем входное напряжение. В электронных схемах часто оказывается необходимым уменьшить уровень напряжения сигнала. Наиболее легко это можно осуществить при помощи двухрезисторной схемы, известной как делитель напряжения. Входное напряжение прикладывается параллельно к двум резисторам, а выходное напряжение снимается с одного из этих резисторов. Сопротивления этих резисторов выбираются таким образом, чтобы выходное напряжение составляло некоторую определенную часть от входного напряжения. Рис. 7-1. Широко используемый делитель напряжения показан на рисунке 7-1. Вы можете использовать закон Ома для расчета выходного напряжения, если известны входное напряжение и сопротивления резисторов. Тем не менее, следующая формула ускоряет и упрощает процесс вычислений. Vo = VsR2/(R1 + R2) Вычисление выходного напряжения в соответствии с приведенной выше формулой предполагает, что в схеме нет нагрузки. Если параллельно резистору R2 подключена резистивная нагрузка с конечным сопротивлением, выходное напряжение будет меньше, чем вычисленное, по формуле. Если сопротивление нагрузки приближается к сопротивлению R2, нагрузка будет отбирать все больше и больше тока из схемы. Это приведет к перераспределению падений напряжения в схеме, и выходное напряжение будет уже значительно отличаться от рассчитанного в соответствии с приведенной выше формулой напряжения. Для определения выходного напряжения делителя при наличии нагрузки Вы можете использовать стандартные методы расчетов в соответствии с законами Ома и Кирхгофа, которые уже применялись Вами в предыдущем эксперименте, чтобы дать заключение о выходном напряжении. Во многих приложениях, тем не менее, это не является необходимым. Если сопротивление нагрузки достаточно велико в сравнении со значением R2, выходное напряжение будет почти равным напряжению, значение которого получается в соответствии с приведенной выше формулой. При этом эмпирическим правилом является: сопротивление нагрузки должно в десять или более раз превышать сопротивление R2. Чем выше значение сопротивления нагрузки по отношению к R2, тем ближе выходное напряжение будет к значению, рассчитанному в соответствии с приведенной ранее формулой. Потенциометр Одним из наиболее часто используемых электроэлементов является потенциометр, который фактически представляет собой варьируемый делитель напряжения. Потенциометр — это переменный резистор с тремя выводами (см. рис. 7-2). Центральный вывод соединен с подвижным контактом, который может соединяться с любой точкой резистивного элемента, позволяя гасить часть полного приложенного напряжения. Подвижный контакт может перемещаться от одного конца резистивного элемента к другому, позволяя выбирать любое значение напряжения между напряжением входного источника и нулем. Потенциометры широко используются в электронных схемах, поскольку с их помощью удается точно выполнить настройку выходного напряжения, желательного для конкретного применения. Рис. 7-2. Краткое содержание В данном эксперименте Вы соберете и продемонстрируете резистивные делители напряжения, а также покажете изменение выходного напряжения при различных уровнях нагрузки. Вы также продемонстрируете использование потенциометра в качестве варьируемого делителя напряжения. ПРОЦЕДУРА 1. Обратитесь к схеме делителя напряжения, показанной на рисунке 7-3. Выполните расчет выходного напряжения с нагрузкой 1 кОм и без нее. Vo=___В (нагрузка 1 кОм) Vo = ________ В (без нагрузки) Рис. 7-3. 2. Соберите схему, показанную на рисунке 7-3. Не присоединяйте резистор 1 кОм. Измерьте выходное напряжение на R2. Это напряжение без нагрузки. Vo=_______В 3. Присоедините нагрузочный резистор 1 кОм параллельно R2, как показано на рисунке 7-3. Измерьте выходное напряжение с подключенной нагрузкой. После этого отсоедините нагрузку 1 кОм и замените ее резистором 10 кОм. Снова измерьте выходное напряжение. Наконец, замените резистор 10 кОм на резистор 100 кОм. Измерьте выходное напряжение. Запишите значения выходных напряжений в таблицу. 4. Основываясь на данных, накопленных в шаге З, укажите, как варьируется выходное напряжение в зависимости от различных сопротивлений нагрузки. 5. Размонтируйте схему на рисунке 7-3. Смонтируйте потенциометр 10 кОм на Вашей макетной панели. Каждый из контактов должен входить в отверстие на отдельном вертикальном ряду отверстий макетной панели. Центральный контакт — это подвижный контакт. Затем подключите к потенциометру источник питания 9 В, как показано на рисунке 7-4. Вы будете измерять выходное напряжение между отрицательным выводом источника и подвижным контактом потенциометра. 6. Подключите Ваш мультиметр на выход потенциометра для измерения выходного напряжения (Vo). При помощи небольшой отвертки полностью выведите подвижный контакт потенциометра против часовой стрелки. Запишите полученное выходное напряжение. Затем полностью выведите подвижный контакт потенциометра по часовой стрелке. Снова запишите полученное выходное напряжение. Vo=___В (против часовой стрелки) Vo=__В (по часовой стрелке) 7. Теперь контролируйте выходное напряжение потенциометра. Отрегулируйте Ваш потенциометр таким образом, чтобы выходное напряжение составляло половину входного напряжения (напряжения источника питания). Рис. 7-4. 8. Размонтируйте схему рисунка 7-4. 9. Используя Ваш мультиметр, измерьте сопротивление между центральным выводом (подвижный контакт) и каждым из других выводов потенциометра. Запишите полученные значения. Сопротивление между центральным контактом и одним выводом = ______ Ом Сопротивление между центральным контактом и другим выводом = ______ Ом Объясните полученные Вами значения. Рис. 7-5. 10. Соберите делитель напряжения, показанный на рисунке 7-5. Рассчитайте, в каком диапазоне может варьироваться выходное напряжение при использовании потенциометра. Vo = __ В (против часовой стрелки) Vo = _____ В (по часовой стрелке) 11.Подключите схему к источнику питания. Измеряйте теперь выходное напряжение схемы, варьируя положение подвижного контакта потенциометра по всему его диапазону. Запишите предельные значения напряжения. Vo = __ В (против часовой стрелки) Vo = _____ В (по часовой стрелке) ОБЗОРНЫЕ ВОПРОСЫ 1. Делитель напряжения, аналогичный показанному на рисунке 7-1, имеет следующие сопротивления резисторов: R1 = 10 кОм и R2 = 1 кОм. Источник питания дает напряжение 15В. Выходное напряжение составляет: а) 1, 28 В, б) 1, 36 В, в) 1, 5 В, г) 1, 72 В. 2. Каково минимальное значение сопротивления нагрузки, которая может подключаться к делителю напряжения из вопроса 1, чтобы выходное напряжение не снижалось значительно? а) 100 Ом, б) 1 кОм, в) 10 кОм, г) 100 кОм. 3. Варьируемый делитель напряжения — это: а) потенциометр, б) переменный резистор, в) реостат, г) варистор. 4. Постоянное напряжение 6 В приложено к потенциометру. Выходное напряжение может быть установлено на любое значение в диапазоне: а) от —6 до+ 6 В, б) от 0 до 6 В, в) от 0 до 9 В, г) от 0 до 12 В. 5. Потенциометр из вопроса 4 настроен так, чтобы гасить 85% приложенного напряжения. При этом выходное напряжение составляет: а) 0, 9 В, б) 2, 6 В, в) 4, 3 В, г) 5, 1 В. lib.qrz.ru Делитель напряжения на резисторах — это схема, позволяющая получить из высокого напряжения пониженное напряжение. Используя всего два резистора, мы можем создать любое выходное напряжение, составляющее меньшую часть от входного напряжения. Делитель напряжения является фундаментальной схемой в электронике и робототехнике. Для начала рассмотрим электрическую схему и формулу для расчета. Для того, чтобы разобраться в принципе работы резисторного делителя напряжения и понять, как рассчитать делитель напряжения на резисторах, следует ознакомиться с его принципиальной схемой (см. картинку ниже — несколько вариантов изображения делителя). Схема включает в себя входное напряжение и два резистора. Резистор, находящийся ближе к плюсу входного напряжения Vвх, обозначен R1, резистор находящийся ближе к минусу обозначен R2. Падение напряжения Vвых — это пониженное выходное напряжение, полученное в результате резисторного делителя напряжения. Для расчета выходного напряжения необходимо знать три величины из приведенной схемы — входное напряжение и сопротивление обоих резисторов. Расчет делителя напряжения на резисторах основан на законе Ома. Эта формула показывает, что выходное напряжение резисторного делителя прямо пропорционально входному напряжению и обратно пропорционально отношению сопротивлений R1 и R2. На этом принципе работают потенциометры (переменные резисторы) и многие резистивные датчики, например, датчик освещенности на фоторезисторе. Смотрите калькулятор делителя напряжения на резисторах онлайн. xn--18-6kcdusowgbt1a4b.xn--p1ai Входное сопротивление ЭП определяется как отношение малого приращения входного напряжения к изменению входного тока. Предположим, что в схеме на рис.2.1 в качестве сопротивления нагрузки выступает сопротивление R1. Для рассматриваемой схемы входное напряжение - это напряжение на базе транзистора, а входной ток - ток базы. Входное сопротивление ЭП может быть определено по формуле rвх = dUвх/dIвх= (dUбэ+dUвых)/dIб=dUбэ/dIб+dUвых/dIб=rбэ+R1dIэ/dIб=rбэ+ (β+1)R1, где- коэффициент усиления транзистора по току. Итак входное сопротивление эмиттерного повторителя равно rвх=rбэ+ (β+1)R1. Пример. Найдем входное сопротивление эмиттерного повторителя при следующих исходных данных: ток коллектораIк= 1 мА,R1= 3 кОм, β = 100. rвх=rбэ+ (β+1)R1= βuт /Iк+(β+1)R1= =100 25,5мВ/ 1 мА + 101 3 кОм = 2,55 кОм + 303 кОм = 305,6 кОм. Из расчета видно, что в общем входном сопротивлении доля первого слагаемого (rбэ) незначительная, поэтому часто использую более приближенную формулу для определения выходного сопротивления эмиттерного повторителя ЭП определяется, как отношение изменения выходного напряжения к изменению выходного тока rвых= -dUвых/dIвыхпри условии, что входное напряжение не изменяется, т.е.Uвх=const, аdUвх= 0. Для определения выходного сопротивления рассмотрим схему на рис.2.3. здесь Rист– сопротивление источника входного сигнала. rвых= -dUвых/dIвых= -dUвых/dIэ. (2.3) dUвх =dURист+dUбэ+dUвых. Учитывая, что dUвх= 0, и пренебрегаяdUбэполучим dUвых= -dURист= -dIбRист= -dIэRист /(β+1). Подставим, найденное значение dUвыхв формулу (2.3) и найдем выходное сопротивление усилителя rвых= Rист/(1+). Из формулы видно, что выходное (внутреннее) сопротивление источника входного сигнала уменьшается в (+1) раз при подключении ЭП. Схема на рис.2.1 пропускает на выход сигнал, который больше, чем 0.6В (Uбэоткрытого транзистора). Для того, чтобы схема могла усиливать разнополярные сигналы необходимо создатьсмещение, которое обеспечивает протекание коллекторного тока в течение полного периода сигнала. Смещение обеспечивается путем подачи положительного постоянного напряжения на базу транзистора. Переменный входной сигнал складывается с постоянным напряжением смещения. Величина напряжения смещения должна быть такой величины, чтобы при отрицательной амплитуде входного сигнала напряжение на базе было больше 0,6 В, т.е. транзистор был открыт. Смещение в усилителе можно задавать с помощью делителя напряжения R1, R2, как показано на рис.2.4. R1и R2выбраны так, чтобы на выходе формировался максимальный симметричный сигнал. Это можно обеспечить, если напряжение на эмиттере транзистора при отсутствии входного сигнала будет равно примерно половине напряжения питания Uп.При подаче на вход переменного напряжения на эмиттере сигнал будет изменяться относительно напряжения Uп / 2. Процесс выбора рабочих напряжений в схеме при отсутствии входного сигнала называетсяустановкой рабочей точки. Сопротивления R1и R2выбираются из условия, что ток протекающий через делитель (ток через сопротивление R2) должен быть намного больше ( по крайней мере в 10 раз) тока базы транзистора, чтобы изменение тока базы при изменении входного сигнала оказывало малое влияние на изменение постоянной составляющей тока делителя. Разделительная емкость С1не пропускает постоянное напряжение смещения на вход источника сигнала, а емкость С2пропускает в нагрузку только переменный полезный сигнал. Разделительные емкости С1и С2образуют фильтры верхних частот, нижняя граничная частота которых должна быть выбрана так, чтобы полностью пропускались нижние частоты сигнала. Величины емкости могут быть определены по формуле С 1/ 2fRэкв, где Rэквдля вычисления С1 равно параллельному соединению сопротивлений R1,R2 и rвх. Для определения С2 предполагаем, что сопротивление нагрузки ЭП будет не меньше R3. Поэтому Rэквв этом случае выбирают равным R3. Результаты моделирования схемы, показанной на рис.2.4 представлены на рис.2.5. Из рисунка видно, что выходное напряжение v(5) практически полностью повторяет входное напряжение v(3). Переменное напряжение на базе v(1), по амплитуде равное входному напряжению, изменяется относительно постоянного напряжения смещения, примерно равное 7,5 В. Напряжение на эмиттере v(4) меньше напряжения на базе на Uбэ ≈ 0 studfiles.net 2.7. Делитель напряжения Достаточно часто в некоторых участках схемы необходимо иметь величину напряжения меньше, чем напряжение источника питания. В этом случае можно использовать делитель напряжения на резисторах (рис. 2.5а). Изменяя соотношение между величинами сопротивлений R1 и R2, на выходе делителя можно получить любое значение напряжения, но не более входного. Выходное напряжение делителя при бесконечно большом сопротивлении нагрузки можно рассчитать по формуле (2.14) Для объяснения принципа работы электронных схем необходимо хорошо представлять работу делителя напряжения на резисторах. Можно выделить три задачи, которые необходимо быстро решать при рассмотрении принципа работы электронных устройств, содержащих делитель напряжения: 1. Как и почему изменяется выходное напряжение делителя, если входное напряжение не изменяется (постоянное напряжение или переменное напряжение с неизменяющейся со временем амплитудой), сопротивление резистора R2 не изменяется, а сопротивление резистора R1 увеличивается (уменьшается)? 2. Как и почему изменяется выходное напряжение делителя, если входное напряжение не изменяется (постоянное напряжение или переменное напряжение с неизменяющейся со временем амплитудой), сопротивление резистора R1 не изменяется, а сопротивление резистора R2 увеличивается (уменьшается)? 3. Как и почему изменяется выходное напряжение делителя, если сопротивления резисторов R1, R2 не изменяются, а входное напряжение увеличивается (уменьшается)? Для всех трех задач дать ответ на поставленный вопрос можно, проанализировав формулу (2.14) для определения выходного напряжения делителя. Решить указанные задачи можно и другим способом. В первой задаче для определения изменения выходного напряжения воспользуемся формулой Uвых=Iд×R2. Так как сопротивление резистора R2 неизменно, то для ответа на вопрос задачи достаточно выяснить, как будет изменяться ток Iд при увеличении (уменьшении) сопротивления резистора R1. При увеличении сопротивления резистора R1 общее сопротивление последовательно соединенных резисторов R1 и R2 будет увеличиваться и при неизменном входном напряжении делителя будет уменьшаться ток делителя Iд (по закону Ома для участка цепи). Уменьшение тока делителя при неизменном сопротивлении резистора R2 приведет к уменьшению выходного напряжения. При уменьшении сопротивления резистора R1 сила тока в цепи увеличивается и увеличивается выходное напряжение. Во второй задаче при увеличении сопротивления резистора R2 общее сопротивление цепи увеличится, следовательно, при неизменном входном напряжении сила тока в цепи уменьшится. Использовать формулу Uвых=Iд×R2 для определения изменения выходного напряжения нельзя, так как в этом случае сила тока Iд уменьшается, а сопротивление R2 увеличивается. Поэтому определим сначала, как изменится напряжение U1: U1=Iд×R1. Поскольку сила тока Iдуменьшается, а сопротивление R1 не изменяется, то напряжение U1 уменьшится. Входное напряжение равно сумме напряжений на резисторах R1 и R2: Uвх= U1 +Uвых. Поскольку входное напряжение не изменяется, то при уменьшении напряжения на первом резисторе выходное напряжение (напряжение на втором резисторе) увеличивается. Таким образом, при увеличении сопротивления того резистора делителя, с которого снимается выходное напряжение, выходное напряжение увеличивается, и наоборот. В третьей задаче при увеличении (уменьшении) входного напряжения выходное напряжение делителя увеличивается (уменьшается), поскольку увеличивается (уменьшается) сила тока Iд. Сопротивления резисторов делителя при конечном значении сопротивления нагрузки (рис. 2.5 б, в) можно рассчитать по формулам: где Uвх и Uвых - входное и выходное напряжение делителя, а Iди Iн - ток делителя и ток нагрузки. Делители напряжения рекомендуется использовать при малой силе тока нагрузки и небольших ее колебаниях. В качестве делителя можно использовать потенциометры, в которых плавно изменяется отношение входного и выходного напряжений (рис. 2.5 в). При регулировках в цепях постоянного напряжения дополнительно к делителю напряжения на переменном резисторе широко используют усилитель тока на биполярном транзисторе (рис. 2.5 г). Такая схема подключения нагрузки позволяет получить существенно больший ток при тех же значениях выходного напряжения. Транзистор VT1 желательно взять составным, так как такой транзистор имеет большой коэффициент усиления по току. Иногда требуется очень точно и плавно регулировать выходное напряжение делителя. Такую задачу можно решить, используя одну из двух схем делителя, приведенных на рисунке 2.6. Если в схеме рисунка 2.6а сопротивление резистора R3 существенно больше сопротивления резистора R4, то резистором R2 осуществляют грубую регулировку выходного напряжения, а резистором R1 – точную. В схеме рисунка 2.6 б сопротивление резистора R1 выбирают меньше сопротивления резистора R2 и резистором R2 выходное напряжение регулируют грубо, а резистором R1 – точно. ivatv.narod.ru 2.1. Постановка задачи Обозначить сопротивления элементов схемы в общем виде как RH; jXL; -jXC вывести формулу для комплексной амплитуды напряжения на нагрузке U2m через комплексную амплитуду входного напряжения U1m. Полученное выражение записать, пригодном для каждой гармоники. 2.2. Расчет U2m Расчетная схема представлена на рис. 3. Рис. 3. Расчетная схема . Составим уравнение на основании закона Кирхгофа для напряжений контура : (3) , где (4) Ток (5) Подставим полученное выражение для тока в уравнение (4). После чего решим уравнение (3) относительно напряжения . В результате получим: (6) Полученное выражение запишем в виде, пригодном для гармоники любого порядка. При этом учтём, что XL(k)=kL; XC(k)=1/kC: (7) Подставив числовые значения параметров, получим: 3. РАСЧЕТ КОМПЛЕКСНЫХ АМПЛИТУД НАПРЯЖЕНИЯ 3.1. Формулировка задачи Используя полученное выражение (7), определить комплексную амплитуду напряжения на выходе (на нагрузке) для постоянной составляющей и гармонических составляющих 1 и 3 порядка. 3.2. Определение комплексных амплитуд напряжения Расчетная схема для постоянной составляющей и гармоник первого и третьего порядка входного напряжения приведена на рис. 4. Рис. 4. . Расчетная схема для 0,1 и 3 гармоник 3.2.1. Расчет постоянной составляющей (нулевой гармоники) напряжения на нагрузке. Расчетная схема приведена на рис. 5. Рис. 5. Расчетная схема для нулевой гармоники напряжения на нагрузке Так как при k=0 XC=, а XL=0, то ветви с емкостями необходимо разомкнуть , а ветвь с индуктивностью – замкнуть. В этом случае из схемы на рис. 5 следует: U2(0)=U1(0). Тот же результат получается и при подстановке значений U1(0) и k = 0в формулу (7). Исходя из (2) , U1(0)=Um/2=19,15 (B) и k=0. Тогда: 3.2.2. Расчет комплексной амплитуды первой гармоники напряжения на нагрузке Расчетная схема приведена на рис. 6. Рис. 6. Расчетная схема для первой гармоники напряжения на нагрузке Исходя из (2),U1m(1)=2Um/=24,38 (B) и k=1. Тогда: 3.2.3. Расчет комплексной амплитуды третьей гармоники напряжения на нагрузке. Расчетная схема приведена на рис. 7. Рис. 7. Расчетная схема для третьей гармоники напряжения. Исходя из (2), U1m(3)=2Um/3=8,128 (B) и k=3. Тогда: 4. РАСЧЕТ НАПРЯЖЕНИЯ НА НАГРУЗКЕ 4.1. Формулировка задачи Записать мгновенное значение напряжения на нагрузке в виде ряда Фурье. 4.2. Разложение напряжения на нагрузке в ряд Фурье Запишем выражения для мгновенных значений напряжения u2(t), воспользовавшись найденными комплексными амплитудами для 0,1 и 3 гармоник: Мгновенное значение напряжения на нагрузке в виде ряда Фурье: 5.1. Формулировка задачи Построить друг под другом линейчатые спектры входного u1 и выходного u2 напряжений. studfiles.net2. Определение комплексной амплитуды выходного напряжения. Входное напряжение формула
Делитель напряжения. Калькулятор расчета делителя напряжения
 Классическая формула делителя напряжения
Классическая формула делителя напряжения Схема классического делителя напряжения на 2 резистора
Схема классического делителя напряжения на 2 резистораУпрощения
 Формула делителя напряжения, если сопротивления равны
Формула делителя напряжения, если сопротивления равны Формула делителя напряжения, если R2 на порядок больше R1
Формула делителя напряжения, если R2 на порядок больше R1 Вы можете воспользоваться онлайн калькулятором ниже, чтобы проверить как саму классическую формулу делителя напряжения, представленную на рисунке 1, так и вышеприведенные упрощения этой формулы.
Вы можете воспользоваться онлайн калькулятором ниже, чтобы проверить как саму классическую формулу делителя напряжения, представленную на рисунке 1, так и вышеприведенные упрощения этой формулы.7. Делители напряжения

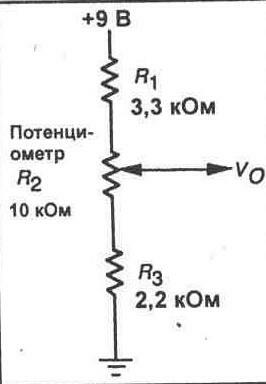
Калькулятор делителя напряжения на резисторах
Как работает делитель напряжения на резисторах
 Расчет делителя напряжения на резисторах онлайн калькулятор
Расчет делителя напряжения на резисторах онлайн калькуляторVвых = R2 х Vвых / R1 + R2
Расчет делителя напряжения на резисторах онлайн
2.2. Входное сопротивление
2.3. Выходное сопротивление
2.4. Смещение в эмиттерном повторителе
Делитель напряжения
2. Определение комплексной амплитуды выходного напряжения
5. Построение линейчатых спектров напряжений
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''










Поделиться с друзьями: