Под последовательным соединением подразумевают случаи, когда два или больше элемента имеют вид цепи, при этом каждый из них соединяется с другим только в одной точке. Зачем конденсаторы так размещаются? Как это правильно сделать? Что необходимо знать? Какие особенности последовательное соединение конденсаторов имеет на практике? Какая формула результата? Увы, но здесь не всё так легко сделать, как может показаться. Многие новички думают, что если на схематическом рисунке написано, что необходим элемент на 49 микрофарад, то достаточно его просто взять и установить (или заменить равнозначным). Но необходимые параметры подобрать сложно даже в профессиональной мастерской. И что делать, если нет нужных элементов? Допустим, есть такая ситуация: необходим конденсатор на 100 микрофарад, а есть несколько штук на 47. Поставить его не всегда можно. Ехать на радиорынок за одним конденсатором? Не обязательно. Достаточно будет соединить пару элементов. Существует два основных способа: последовательное и параллельное соединение конденсаторов. Вот о первом мы и поговорим. Но если говорить про последовательное соединение катушки и конденсатора, то тут особых проблем нет. Когда с ними проводятся такие манипуляции, то электрические заряды на обкладках отдельных элементов будут равны: КЕ=К1=К2=К3. КЕ – конечная емкость, К – пропускаемое значение конденсатора. Почему так? Когда заряды поступают от источника питания на внешние обкладки, то на внутренних может быть осуществлен перенос величины, которая является значением элемента с наименьшими параметрами. То есть если взять конденсатор на 3 мкФ, а после него подсоединить на 1 мкФ – то конечный результат будет 1 мкФ. Конечно, на первом можно будет наблюдать значение в 3 мкФ. Но второй элемент не сможет столько пропустить, и он будет срезать всё, что больше необходимого значения, оставляя большую емкость на первоначальном конденсаторе. Давайте рассмотрим, что нужно рассчитать, когда делается последовательное соединение конденсаторов. Формула: Н=КЕ/ОЕК Для начала не забывайте, что кроме ёмкости они ещё обладают номинальным напряжением. Почему? Когда осуществляется последовательное соединение, то напряжение распределяется обратно пропорционально их ёмкостям между ними самими. Поэтому использовать такой подход имеет смысл только в тех случаях, когда любой конденсатор сможет предоставить минимально необходимые параметры работы. Если используются элементы, у которых одинаковая емкость, то напряжение между ними будет разделяться поровну. Также небольшое предостережение относительно электролитических конденсаторов: при работе с ними всегда внимательно контролируйте их полярность. Ибо при игнорировании этого фактора последовательное соединение конденсаторов может дать ряд нежелательных эффектов. И хорошо, если всё ограничится только пробоем данных элементов. Помните, что конденсаторы копят ток, и если что-то пойдёт не так, в зависимости от схемы может случиться прецедент, в результате которого из строя выйдут другие составляющие схемы. Из-за того, что у него существует только один возможный путь протекания, он будет иметь одно значение для всех конденсаторов. При этом количество накопленного заряда везде обладает одинаковым значением. От емкости это не зависит. Посмотрите на любую схему последовательного соединения конденсаторов. Правая обкладка первого соединена с левой второго и так далее. Если используется больше 1 элемента, то часть из них будет изолированной от общей цепи. Таким образом, эффективная площадь обкладок становится меньшей и равняется параметрам самого маленького конденсатора. Какое физическое явление лежит в основе этого процесса? Дело в том, что как только конденсатор наполняется электрическим зарядом, то он перестаёт пропускать ток. И он тогда не может протекать по всей цепи. Остальные конденсаторы в таком случае тоже не смогут заряжаться. Каждый элемент понемногу рассеивает напряжение. Учитывая, что емкость ему обратно пропорциональна, то чем она меньше, тем большим будет падение. Как уже упоминалось ранее, последовательно соединённые конденсаторы обладают одинаковым электрическим зарядом. Поэтому при делении всех выражений на общее значение можно получить уравнение, которое покажет всю емкость. В этом последовательное и параллельное соединение конденсаторов сильно разнятся. Давайте воспользуемся представленными в статье формулами и рассчитаем несколько практических задач. Итак, у нас есть три конденсатора. Их емкость составляет: С1 = 25 мкФ, С2 = 30 мкФ и С3 = 20 мкФ. Они соединены последовательно. Необходимо найти их общую емкость. Используем соответствующее уравнение 1/С: 1/С1 + 1/С2 + 1/С3 = 1/25 + 1/30 + 1/20 = 37/300. Переводим в микрофарады, и общая емкость конденсатора при последовательном соединении (а группа в данном случае считается как один элемент) составляет примерно 8,11 мкФ. Давайте, чтобы закрепить наработки, решим ещё одну задачу. Имеется 100 конденсаторов. Емкость каждого элемента составляет 2 мкФ. Необходимо определить их общую емкость. Нужно их количество умножить на характеристику: 100*2=200 мкФ. Итак, общая емкость конденсатора при последовательном соединении составляет 200 микрофарад. Как видите, ничего сложного. Итак, мы проработали теоретические аспекты, разобрали формулы и особенности правильного соединения конденсаторов (последовательно) и даже решили несколько задачек. Хочется напомнить, чтобы читатели не упускали из внимания влияние номинального напряжения. Также желательно, чтобы подбирались элементы одного типа (слюдяные, керамические, металлобумажные, плёночные). Тогда последовательное соединение конденсаторов сможет дать нам наибольший полезный эффект. www.syl.ru Схемы в электротехнике состоят из электрических элементов, в которых способы соединения конденсаторов могут быть разными. Надо понимать, как правильно подключить конденсатор. Отдельные участки цепи с подключенными конденсаторами можно заменить одним эквивалентным элементом. Он заменит ряд конденсаторов, но должно выполняться обязательное условие: когда напряжение, подводимое к обкладкам эквивалентного конденсатора, равняется напряжению на входе и выходе группы заменяющихся конденсаторов, тогда заряд емкости будет такой же, как и на группе емкостей. Для понимания вопроса, как подключить конденсатор в любой схеме, рассмотрим виды его включения. Параллельное соединение конденсаторов — это когда все пластины подключаются к точкам включения цепи, образовывая батарею емкостей. Параллельное соединение конденсаторов: Разность потенциалов на пластинах накопителей емкости будет одинаковая, так как они все заряжаются от одного источника тока. В этом случае каждый заряжающийся конденсатор имеет собственный заряд при одинаковой величине, подводимой к ним энергии. Параллельные конденсаторы, общий параметр количества заряда полученной батареи накопителей, рассчитывается, как сумма всех зарядов, помещающихся на каждой емкости, потому что каждый заряд емкости не зависит от заряда другой емкости, входящей в группу конденсаторов, параллельно включенных в схему. При параллельном соединении конденсаторов емкость равняется: Из представленной формулы можно сделать вывод, что всю группу накопителей можно рассматривать как один равноценный им конденсатор. Конденсаторы, соединенные параллельно, имеют напряжение: Когда в схеме выполнено последовательное соединение конденсаторов, оно выглядит как цепочка емкостных накопителей, где пластина первого и последнего накопителя емкости (конденсатора) подключены к источнику тока. Последовательное соединение конденсатора: При последовательном соединении конденсаторов все устройства этого участка берут одинаковое количество электроэнергии, потому что в процессе участвует первая и последняя пластинка накопителей, а пластины 2, 3 и другие до N проходят зарядку посредством влияния. По этой причине заряд пластины 2 накопителя емкости равняется по значению заряду 1 пластины, но имеет обратный знак. Заряд пластины накопителя 3 равняется значению заряда пластины 2, но так же с обратным знаком, все последующие накопители имеет аналогичную систему заряда. Формула нахождения заряда на конденсаторе, схема подключения конденсатора: Когда выполняется последовательное соединение конденсаторов, напряжение на каждом накопители емкости будет различное, так как в зарядке одинаковым количеством электрической энергии участвуют разные емкости. Зависимость емкости от напряжения такова: чем она меньше, тем большее напряжение необходимо подать на пластины накопителя для его зарядки. И обратная величина: чем выше емкость накопителя, тем меньше требуется напряжения для его зарядки. Можно сделать вывод, что емкость последовательно соединенных накопителей имеет значение для величины напряжения на пластинах — чем она меньше, тем больше напряжения требуется, а также накопители большой емкости требуют меньшего напряжения. Основное отличие схемы последовательного соединения накопителей емкости в том, что электроэнергия протекает только в одном направлении, а это означает, что в каждом накопителе емкости составленной батареи ток будет одинаковым. В этом виде соединений конденсаторов обеспечивается равномерное накопление энергии независимо от емкости накопителей. Группу накопителей емкости можно также на схеме рассматривать как эквивалентный накопитель, на пластины которого подается напряжение, определяемое формулой: Заряд общего (эквивалентного) накопителя группы емкостных накопителей последовательного соединения равен: Общему значению емкости последовательно соединенных конденсаторов соответствует выражение: Параллельное и последовательное соединение конденсаторов на одном из участков цепи схемы называется специалистами смешанным соединением. Участок цепи подсоединенных смешанным включением накопителей емкости: Смешанное соединение конденсаторов в схеме рассчитывается в определенном порядке, который можно представить следующим образом: Накопители емкостей (двухполюсники) включены разными способами в цепь, это дает несколько преимуществ в решении электротехнических задач по сравнению с традиционными способами включения конденсаторов: Разного вида включения конденсаторов в цепь применяются для решения электротехнических задач, в частности, для получения полярных накопителей из нескольких неполярных двухполюсников. В этом случае решением будет соединение группы однополюсных накопителей емкости по встречно-параллельному способу (треугольником). В этой схеме минус соединяется с минусом, а плюс — с плюсом. Происходит увеличение емкости накопителя, и меняется работа двухполюсника. Не отображаются имеющиеся вхождения: последовательное параллельное и смешанное соединение конденсаторов, последовательное и параллельное соединение конденсаторов, при параллельном соединении конденсаторов емкость. domelectrik.ru Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может. Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а). Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила. В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода. После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать. Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения. С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления. Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится. Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю. В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях. Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°. Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты. Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты. Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может. Величина емкостного сопротивления определяется по следующей формуле: где Хс — емкостное сопротивление конденсатора в ом; f—частота переменного тока в гц; ω — угловая частота переменного тока; С — емкость конденсатора в ф. При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным. Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь. Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки. Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки. Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины. Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока. Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать. Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей. Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны. В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно. В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д. Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока. Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной. Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно. Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте. И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС. При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи. А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео: ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! www.sxemotehnika.ru Обложка ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА Учебно-методическое пособие к лабораторной работе № 3.3 по дисциплине «Физика» Владивосток 2013 Титул Министерство образования и науки Российской Федерации Дальневосточный федеральный университет Школа естественных наук ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА Учебно-методическое пособие к лабораторной работе № 3.3 по дисциплине «Физика» Владивосток Дальневосточный федеральный университет ____________________________________________________________________________________________________________ Оборот титула УДК 53 (о76.5) ББК 22. 343 Э41 Составитель: О.В.Плотникова Изучение процессов зарядки и разрядки конденсатора. Определение емкости конденсатора: учебно-методич. пособие к лабораторной работе № 3.3 по дисциплине «Физика» / Дальневосточный федеральный университет, Школа естественных наук [сост. О.В.Плотникова]. – Владивосток: Дальневост. федерал. ун-т, 2013. - с. Пособие, подготовленное на кафедре общей физики Школы естественных наук ДВФУ, содержит краткий теоретический материал по теме «Электрическая емкость. Конденсаторы» и инструктаж к выполнению лабораторной работы «Изучение процессов зарядки и разрядки конденсатора. Определение емкости конденсатора» по дисциплине «Физика». Для студентов-бакалавров ДВФУ. УДК 53 (о76.5) ББК 22. 343 ©ФГАОУ ВПО «ДВФУ», 2013 Цель работы: экспериментальное подтверждение законов, описывающие процессы зарядки и разрядки конденсатора, определение постоянной времени электрической цепи, определение неизвестной емкости конденсатора. Краткая теория Электроёмкость. Проводники – это вещества, содержащие большое количество свободных заряженных частиц. В металлических проводниках такими частицами являются свободные электроны, в электролитах – положительные и отрицательные ионы, в ионизированных газах – ионы и электроны. Если рассматривать проводник, рядом с которым нет других проводников, то он называется уединенным. Опыт показывает, что потенциал уединенного проводника прямо пропорционален находящемуся на нем заряду. Отношение заряда, сообщенного проводнику, к его потенциалу называется электроемкостью проводника (или просто емкостью): С= Таким образом, емкость определяется величиной заряда, который надо сообщить проводнику, чтобы увеличить его потенциал на единицу. Емкость зависит от размеров и формы проводника, от диэлектрической проницаемости среды, от наличия рядом других проводников и не зависит ни от заряда, ни от потенциала. Так, для уединенного проводящего шара радиуса R емкость равна: С = 4πεε0R. (т.к. потенциал φ= ). Здесь ε – диэлектрическая проницаемость среды, ε0 - электрическая постоянная. Единица емкости в системе СИ называется Фарадой (Ф). 1Ф = 1. Конденсаторы. Емкостью обладают не только отдельные проводники, но и системы проводников. Система, состоящая из двух проводников, разделенных слоем диэлектрика, называется конденсатором. Проводники в этом случае называются обкладками конденсатора. Заряды на обкладках имеют противоположные знаки, но по модулю – одинаковы. Практически все поле конденсатора сосредоточено между обкладками и. Емкостью конденсатора называется величина С= , (1) где q – абсолютная величина заряда одной из обкладок, U - разность потенциалов (напряжение) между обкладками. В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими, цилиндрическими. Найдем емкость плоского конденсатора, обкладки которого имеют площадь S, расположены на расстоянии d, а пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью ε. Если поверхностная плотность заряда на обкладках равна σ (σ= ), то напряженность поля конденсатора (поле считается однородным) равна: Е= = Разность потенциалов между обкладками связана с напряженностью поля: Е = , откуда получим U=Ed = = Используя формулу ( 1 ), получим для емкости плоского конденсатора выражение: С =(2) Соединение конденсаторов. Используются два основных вида соединения: последовательное и параллельное. При параллельном соединении (рис 1), общая емкость батареи равна сумме емкостей всех конденсаторов: Собщ.= С1 +С2+С3+…=ΣСi . (3) При последовательном соединении (рис.2) величина, обратная общей емкости, равна сумме величин, обратных емкостям всех конденсаторов: . (4) Если последовательно соединены n конденсаторов с одинаковой емкостью С, то общая емкость: Собщ.= Рис. 1.Параллельное соединение. Рис. 2.Последовательное соединение Энергия конденсатора. Если процесс зарядки конденсатора является медленным (квазистационарным), то можно считать, что в каждый момент времени потенциал любой из обкладок конденсатора во всех точках одинаков. При увеличении заряда на величину dq совершается работа , гдеu – мгновенное значение напряжения между обкладками конденсатора. Учитывая, что , получаем:. Если емкость не зависит от напряжения, то эта работа идет на увеличение энергии конденсатора. Интегрируя данное выражение, получим: , где W – энергия конденсатора, U – напряжение между обкладками заряженного конденсатора. Используя связь между зарядом, емкостью конденсатора и напряжением, можно представить выражение для энергии заряженного конденсатора в других видах: . (5) Квазистационарные токи. Процессы зарядки и разрядки конденсатора. При зарядке или разрядке конденсатора в цепи конденсатора течет ток. Если изменения тока происходят очень медленно, то есть за время установления электрического равновесия в цепи изменения токов и э.д.с. малы, то для определения их мгновенных значений можно использовать законы постоянного тока. Такие медленно меняющиеся токи называют квазистационарными. Так как скорость установления электрического равновесия велика, под понятие квазистационарных токов подпадают и довольно быстрые в обычном понимании процессы: переменный ток, многие электрические колебания, используемые в радиотехнике. Квазистационарными являются и токи зарядки или разрядки конденсатора. Рассмотрим электрическую цепь, общее сопротивление которой обозначим R. Цепь содержит конденсатор емкостью C, подключенный к источнику питания с э.д.с. ε (рис. 3). Рис. 3. Процессы зарядки и разрядки конденсатора. Зарядка конденсатора. Применяя к контуру εRC1ε второе правило Кирхгофа, получим: , где I, U – мгновенные значения силы тока и напряжения на конденсаторе (направление обхода контура указано стрелкой). Учитывая, что ,, можно привести уравнение к одной переменной: . Введем новую переменную: . Тогда уравнение запишется: . Разделив переменные и проинтегрировав, получим: . Для определения постоянной А используем начальные условия: t=0, U=0, u= - ε. Тогда получим: А= - ε. Возвращаясь к переменной , получим окончательно для напряжения на конденсаторе выражение: . (6) С течением времени напряжение на конденсаторе растет, асимптотически приближаясь к э.д.с. источника (рис.4, I.). Разрядка конденсатора. Для контура CR2C по второму правилу Кирхгофа: RI=U. Используем также: , и (ток течет в обратном направлении). Приведя к переменной U, получим: . Интегрируя, получим: . Постоянную интегрирования B определим из начальных условий: t=0, U=ε. Тогда получим: В=ε. Для напряжения на конденсаторе получим окончательно: . (7) С течением времени напряжение падает, приближаясь к 0 (рис. 4, II). Рис. 4. Графики зарядки (I) и разрядки (II) конденсатора. Постоянная времени. Характер протекания процессов зарядки и разрядки конденсатора (установление электрического равновесия) зависит от величины: , (8) которая имеет размерность времени и называется постоянной времени электрической цепи. Постоянная времени показывает, через какое время после начала разрядки конденсатора напряжение уменьшается в e раз (е=2,71). Теория метода Прологарифмируем выражение (7): (учли, что RC=τ). График зависимости lnU от t (линейная зависимость) выражается прямой линией (рис.5), пересекающей ось y (lnU) в точке с координатами (0; lnε). Угловой коэффициент К этого графика и будет определять постоянную времени цепи: ,откуда: . (9) Рис. 5. Зависимость натурального логарифма напряжения от времени при разрядке конденсатора Используя формулы: и ,можно получить, что для одного и того же интервала времени : . Отсюда: .(10) Экспериментальная установка Установка состоит из основного блока – измерительного модуля, имеющего клеммы для подключения дополнительных элементов, источника питания, цифрового мультиметра и набора минимодулей с различными значениями сопротивления и емкости. Для выполнения работы собирается электрическая цепь в соответствии со схемой, изображенной на верхней панели модуля. В гнезда «R1» подключается минимодуль с номиналом 1Мом, в гнезда «R2»- минимодуль с номиналом 100Ом. Параметры исследуемого конденсатора, подключаемого в гнезда «С», задаются преподавателем. В гнезда подключения амперметра устанавливается перемычка. В гнезда вольтметра подключается цифровой мультиметр в режиме вольтметра. Следует отметить, что сопротивления резисторов заряда-разряда (минимодулей) R и цифрового вольтметра RV образуют делитель напряжения, что приводит к тому, что фактически максимальное напряжение на конденсаторе будет равно не ε, а , где r0- сопротивление источника питания. Соответствующие поправки необходимо будет вносить и при вычислении постоянной времени. Однако, если входное сопротивление вольтметра (107Ом) значительно превышает сопротивление резисторов, и сопротивление источника мало, то данными поправками можно пренебречь. Порядок выполнения работы Собрать электрическую цепь с заданным преподавателем значением емкости. Тумблер (переключатель заряда-разряда) установить в среднее положение (стоп). Переключатель предела измерения цифрового мультиметра установить в положение «20В» (режим измерения постоянного напряжения). Подключить модуль к сети переменного тока (клавиша включения на задней панели модуля) и установить выходное напряжение , заданное преподавателем (6,5В-15В). Включить цифровой мультиметр. Нажатием кнопки «Сброс» подготовить модуль к началу измерений. Тумблер перевести в положение «Заряд». При этом запускается секундомер, и начинает меняться напряжение на конденсаторе (показания вольтметра). Довести напряжение на конденсаторе до значения примерно 0,8ε. Сбросить показания секундомера нажатием кнопки «Сброс». Перевести тумблер в положение «Разряд» и измерять напряжения на конденсаторе при его разрядке с интервалом времени 5с. Занести данные в таблицу 1. Подключить в цепь конденсатор с неизвестным значением емкости и повторить измерения по п. 4. Данные занести в таблицу 2. Подключить в цепь конденсатор и резистор с другим известным значением емкости. Повторить измерения по п. 4. Данные занести в таблицу 3. Нажать кнопку «Сброс». Выключить источник питания и мультиметр. Отключить от сети измерительный модуль и отсоединить от него дополнительные элементы. Таблица 1 ε= В, R1= Ом, , С1= Ф Разрядка t (с) U (В) lnU τ1±Δτ1 (с) Таблица 2 ε= В, R1= Ом, Сх=? Ф Разрядка t (с) U (В) lnU τх±Δτх (с) Сх±ΔСх (Ф) Таблица 3 ε= В, R2= Ом, С2 = Ф Разрядка t (с) U (В) lnU τ2±Δτ2 (с) Обработка результатов измерения По результатам измерений студенты выполняют одно из следующих заданий (по указанию преподавателя). Задание 1. Построение кривых разрядки конденсаторов и экспериментальное подтверждение закона, описывающего данный процесс. Используя данные, взятые из таблиц 1 и 3, постройте графики зависимости напряжения от времени при разрядке конденсаторов С1и С2. Проанализируйте их, сравните с теоретическими (рис. 4). Постройте графики разрядки конденсаторов С1и С2 в осях (lnU, t). Проанализируйте их, сравните с теоретическими (рис. 5). Определите по графикам угловые коэффициенты К1и К2. Среднее значение углового коэффициента находится как отношение, определяющее тангенс угла наклона прямой: . Случайные погрешности графическим методом можно оценить по отклонению опытных точек относительно проведенной прямой. Относительная погрешность углового коэффициента может быть найдена согласно формуле: , где δ(lnU) – отклонение (в проекции на ось lnU) от прямой линии наиболее удаленной опытной точки, - интервал, на котором сделаны измерения. По значениям угловых коэффициентов определите постоянные времени τ1 и τ2, используя формулу (9). Сравните полученные значения со значениями постоянной времени, рассчитанными по формуле (8). Посчитайте относительные и абсолютные погрешности для постоянной времени: ,. Сделайте выводы о соответствии экспериментальных графиков экспоненциальному виду зависимости напряжения от времени, и о влиянии постоянной времени на протекание процессов зарядки и разрядки конденсатора. Задание 2. Определение неизвестной емкости конденсатора. Используя данные, взятые из таблиц 1 и 2, постройте графики зависимости напряжения от времени при разрядке конденсаторов С1 и Сх. Проанализируйте их, сравните с теоретическими (рис. 4). Постройте графики разрядки конденсаторов С1 и Сх в осях (lnU, t). Сравните их и сделайте вывод о соотношении постоянных времени (см. рис.5). Определите по формуле (10) неизвестную емкость, используя графики и данные таблиц 1 и 2. Найдите относительные погрешности угловых коэффициентов εК1 и εкх(см. п.4 задания 1). Определите относительную и абсолютную погрешности емкости: , . Сравните полученное значение Сх со значением, измеренным при помощи цифрового мультиметра в режиме измерения емкости. Сделайте вывод. Дополнительное задание. Рассчитайте энергию заряженного конденсатора, используя формулу (5). Контрольные вопросы Что представляет собой конденсатор? Что называется емкостью конденсатора? Докажите, что электрическое поле плоского конденсатора сосредоточено между его обкладками. 2. Сколько надо взять конденсаторов емкостью 2мкФ и как их соединить, чтобы получить общую емкость 5 мкФ? Как можно найти энергию заряженного конденсатора? Какие токи называются квазистационарными? Почему токи зарядки и разрядки конденсатора можно отнести к квазистационарным? По какому закону изменяется напряжение на конденсаторе в процессах а) зарядки и б) разрядки? Что показывает постоянная времени цепи? От чего она зависит? Зачем в данной работе строится график зависимости lnU от t? Как в данной работе определяется постоянная времени электрической цепи? ЛИТЕРАТУРА 1.Трофимова Т.И. Курс физики. / Т.И. Трофимова. - М.: Высшая школа, 2006-2009 г. г. – 544с. 2 Савельев И.В. Курс физики. В 3-х томах. Том 2. Электричество. Колебания и волны. Волновая оптика. Изд. 3-е, стереотип. / И.В. Савельев - М.: Лань, 2007. - 480 с. 3. Грабовский Р. И. Курс физики / Р.И. Грабовский - СПб: издательство «Лань», 2012. – 608с. 4 Зисман Г. А., Тодес О. М. Курс общей физики. В 3-х томах. Том 2. Электричество и магнетизм / Г.А. Зисман, О.М. Тодес - СПб: «Лань», 2007. - 352c. Концевой титул Учебное издание Составитель: Плотникова Ольга Васильевна ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА. ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА Учебно-методическое пособие к лабораторной работе № 3.3 по дисциплине «Физика» В авторской редакции Компьютерная верстка Подписано в печать Формат 60х84/16. Усл.печ.л. Уч.-изд.л. Тираж экз. Заказ Дальневосточный федеральный университет 690091, г. Владивосток, ул. Суханова, 8 Отпечатано на кафедре общей физики ШЕН ДВФУ 690091, г. Владивосток, ул. Суханова, 8 studfiles.net Опубликовано Июль 30, 2015 Все наверняка уже знают, что собой представляют последовательное и параллельное соединения.Соединение, при котором конец одного устройства соединен с началом следующего, называется последовательным. Последовательное соединение конденсаторов При последовательном соединении конденсаторов. получаемая цепь выглядит следующим образом: Эта схема состоит из следующих элементов: трех конденсаторов C1. C2. С3 и источника электрической энергии E . Мы видим, что конденсаторы подключены по всем правилам последовательного соединения, то есть вывод конденсатора C1 соединён с началом конденсатора C2. ну а конец конденсатора C2 соединен с началом третьего конденсатора C3 .Стоит обратить внимание на то, как распределяются ёмкости каждого. При таком соединении, все ёмкостя следующим образом. Дело в том, что общая емкость всех включенных конденсаторов не будит превышать емкости любого из конденсаторов. Проще говоря, если в данной группе конденсаторов, будит конденсатор с наименьшей емкостью, например, в 100 миро фарад, то общая емкость трех конденсаторов не будит превышать этих ста микрофарад.Общую емкость можно рассчитать по следующей формуле: Параллельное соединение конденсаторов При параллельном соединении, начала всех конденсаторов соединяются в одну точку, а концы в другую, как показано на рисунке ниже: Это как два пишем один в уме, только в данном случаи один рисуем, а три в уме. Смешанное соединение конденсаторов Смешанное соединение конденсаторов выглядит следующим образом: Применения параллельного и последовательного соединений конденсаторов нашло свое применение в тех случаях, когда необходимо получить ту или иную величину емкости. Допустим у вас нет подходящего конденсатора, но есть куча других. Выполнив несколько не хитрых расчетов можно подобрать необходимую емкость. Конденсаторы, как и резисторы, можно соединять последовательно и параллельно. Рассмотрим соединение конденсаторов: для чего применяются каждая из схем, и их итоговые характеристики. Параллельное соединение конденсаторов Эта схема – самая распространенная. В ней обкладки конденсаторов соединяются между собой, образуя эквивалентную емкость, равную сумме соединяемых емкостей. При параллельном соединении электролитических конденсаторов необходимо, чтобы между собой соединялись выводы одной полярности. Особенность такого соединения – одинаковое напряжение на всех соединяемых конденсаторах. Номинальное напряжение группы параллельно соединенных конденсаторов равно рабочему напряжению конденсатора группы, у которого оно минимально. Токи через конденсаторы группы протекают разные: через конденсатор с большей емкостью потечет больший ток. На практике параллельное соединение применяется для получения емкости нужной величины, когда она выходит за границы диапазона, выпускаемого промышленностью, или не укладываются в стандартный ряд емкостей. В системах регулирования коэффициента мощности (cos ϕ) изменение емкости происходит за счет автоматического подключения или отключения конденсаторов в параллель. Последовательное соединение конденсаторов При последовательном соединении обкладки конденсатором соединяются друг к другу, образуя цепочку. Крайние обкладки подключаются к источнику, а ток по всем конденсаторам группы потечет одинаковый. Эквивалентная емкость последовательно соединенных конденсаторов ограничена самой маленькой емкостью в группе. Объясняется это тем, что как только она полностью зарядится, ток прекратится. Подсчитать общую емкость двух последовательно соединенных конденсаторов можно по формуле Но применение последовательного соединения для получения нестандартных номиналов емкостей не так распространено, как параллельного. При последовательном соединении напряжение источника питания распределяется между конденсаторами группы. Это позволяет получить батарею конденсаторов, рассчитанную на большее напряжение. чем номинальное напряжение входящих в нее компонентов. Так из дешевых и небольших по размерам конденсаторов изготавливаются блоки, выдерживающие высокие напряжения. Еще одна область применения последовательного соединения конденсаторов связана с перераспределением напряжений между ними. Если емкости одинаковы, напряжение делится пополам, если нет – на конденсаторе большей емкости напряжение получается большим. Устройство, работающее на этом принципе, называют емкостным делителем напряжения . Пример смешанного соединения конденсаторов Такие схемы существуют, но в устройствах специального назначения, требующие высокой точности получения величины емкости, а также для их точной настройки. Оцените качество статьи. Нам важно ваше мнение: В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой. При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4 . В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ = Q1 = Q2 = Q3 . Если рассмотреть три конденсатора С1. С2 и С3. соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов. Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи. Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3 . Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе. Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов. Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3 . Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом. Источники: http://white-santa.ru/soedinenie_kondensatorov/, http://electric-tolk.ru/sposoby-soedineniya-kondensatorov/, http://electric-220.ru/news/soedinenie_kondensatorov/2016-12-20-1143 electricremont.ru Последовательное соединение конденсаторов – батарея, образованная цепочкой конденсаторов. Отсутствует ветвление, выход одного элемента подключается к входу следующего. При последовательном соединении конденсаторов заряд каждого равноценен. Обусловлено природным принципом равновесия. С источником соединены только крайние обкладки, другие заряжаются путем перераспределения меж ними зарядов. Используя равенство, находим: q = q1 = q2 = U1 C1 = U2 C2, откуда запишем: U1/U2 = C2/C1. Напряжения меж конденсаторами распределяются обратно пропорционально номинальным емкостям. В сумме оба составляют вольтаж питающей сети. При разряде конструкция способна отдать заряд q вне зависимости от того, сколько конденсаторов включено последовательно. Емкость батареи найдем из формулы: C = q/u = q/(U1 + U2), подставляя выражения, приведенные выше, приводя к общему знаменателю: 1/С = 1/С1 + 1/С2. При последовательном соединении конденсаторов в батарею складываются величины, обратные номинальным емкостям. Приводя последнее выражение к общему знаменателю, переворачивая дроби, получаем: С = C1C2/(C1 + C2). Выражение используется для нахождения емкости батареи. Если конденсаторов более двух, формула усложняется. Для нахождения ответа номиналы перемножаются меж собой, выходит числитель дроби. В знаменатель ставят попарные произведения двух номиналов, перебирая комбинации. Практически иногда удобнее вести вычисление через обратные величины. Полученным результатом разделить единицу. Соединение последовательное конденсаторов Формула сильно упрощается, если номиналы батареи одинаковы. Требуется просто цифру поделить общим числом элементов, получая результирующее значение. Напряжение распределится равномерно, следовательно, достаточно номинал питающей сети разбить поровну на общее число. При питании аккумулятором 12 вольт, 4-х емкостях, на каждой упадет 3 вольта. Одно упрощение сделаем для случая, когда номиналы равны, одна емкость включена переменная, чтобы подстраивать результат. Тогда максимальное напряжение каждого элемента удастся приближенно найти, разделив вольтаж источника уменьшенным на единицу количеством. Получится результат с заведомым запасом. Что касается переменной емкости, требования намного жёстче. В идеале рабочее значение перекрывает вольтаж источника. На первый взгляд идея соединения конденсаторов батареей последовательным образом покажется лишенной смысла. Первое преимущество очевидно: падают требования к максимальному напряжению обкладок. Больше рабочий вольтаж, дороже изделие. Подобным образом мир видит радиолюбитель, владеющий рядом низковольтных конденсаторов, желающий применить железо составной частью высоковольтной цепи. Рассчитывая по приведенным выше формулам действующие напряжения элементом, можно легко решить поставленную задачу. Рассмотрим для пущей наглядности пример: Пусть установлены аккумулятор напряжением 12 вольт, три емкости номиналами 1, 2 и 4 нФ. Найдем напряжение при последовательном соединении элементов батареей. Решение: Для нахождения трех неизвестных потрудитесь составить равное количество уравнения. Известно из курса высшей математики. Результат будет выглядеть следующим образом: Не сложно заметить, последние два выражения подставим первому, выразив 12 вольт через вольтаж третьего конденсатора. Получится следующее: 4U3 + 2U3 + U3 = 12, откуда находим, напряжение третьего конденсатора составляет 12/7 = 1,714 вольта, U2 – 3,43 вольта, U1 – 6,86 вольта. Сумма чисел дает 12, каждое меньше напряжения питающего аккумулятора. Причем тем больше разница, чем меньший номинал у соседей. Из этого правила следует: в последовательном соединении конденсаторы низкой емкости показывают большее рабочее напряжение. Найдем для определенности номинал составленной батареи, заодно проиллюстрируем формулу, поскольку выше описана чисто словесно: С = С1С2С3/(С1С2 + С2С3 + С1С3) = 8/(2 + 8 + 4) = 8/14 = 571 пФ. Результирующий номинал меньше каждого конденсатора, составляющего последовательное соединение. Из правила видно: максимальное влияние на суммарную емкость оказывает меньший. Следовательно, при необходимости подстройки полного номинала батареи должен быть переменный конденсатор. В противном случае поворот винта не окажет большого влияния на конечный результат. Видим очередной подводный камень: после подстройки распределение напряжений по конденсаторам изменится. Просчитайте крайние случаи, дабы вольтаж не превысил рабочее значение для составляющих батарею элементов. Помимо онлайн- калькуляторов расчета последовательного соединения конденсаторов присутствуют и инструменты помощнее. Большой минус общедоступных средств объясняется нежеланием сайтов проверять программный код, значит, содержат ошибки. Плохо, если одна емкость выйдет из строя, сломленная процессом испытаний неправильно собранной схемы. Не единственный недостаток. Иногда схемы гораздо сложнее, разобраться комплексно невозможно. В отдельных приборах встречаются фильтры высокой частоты, использующие конденсатор, включенные каскадами. Тогда на схеме помимо замыкания через резистор на землю образуется последовательное соединение емкостей. Обычно не применяют формулу, показанную выше. Принято считать, каждый каскад фильтра существует отдельно, результат прохождения сигнала описывается амплитудно-частотной характеристикой. Графиком, показывающим, как сильно обрежет на выходе спектральную составляющую сигнала. Желающим провести ориентировочные расчеты рекомендуется ознакомиться с программным пакетом персонального компьютера Electronics Workbench. Конструктив выполнен по английским стандартам, потрудитесь учитывать нюанс: обозначение резисторов на электрической схеме изломанным зигзагом. Номиналы, названия элементов будут изложены на иностранный манер. Не мешает пользоваться оболочкой, предоставляющей оператору гору источников питания различного толка. И главное – Electronics Workbench позволит задать контрольные точки на каждой, в режиме реального времени посмотреть напряжение, ток, спектр, форму сигнала. Полагается дополнить проект амперметром, вольтметром, прочими аналогичного толка приборами. При помощи такого программного пакета смоделируете ситуацию, посмотрите, сколько падает напряжения на элементе батареи. Уберегает от громоздких расчетов, намного ускоряя процесс проектирования схемы. Одновременно исключаются ошибки. Легко и просто становится добавлять, удалять конденсаторы с немедленной оценкой результата. Скрин показывает рабочий стол Electronics Workbench 5.12 с собранной электрической схемой последовательного соединения конденсаторов. Каждый емкостью 1 мкФ, одинаковые элементы взяты для целей демонстрации. Чтобы каждый мог без труда проверить правильность. Последовательная батарея конденсаторов Обратим вначале внимание на источник. Переменное напряжение частотой 60 Гц. В стране разработчика действует иной стандарт, нежели российские. Рекомендуется правой кнопкой мыши щелкнуть источник, посетить свойства, выставить: Для буквоедов будет полезно полистать свойства элементов цепи. У источника вольны задать допустимое отклонение напряжения (voltage tolerance) в процентах. Достаточно добавить один резистор размером 1 кОм, цепь становится фильтром верхних частот. Рекомендуется не упрощать действия. Поставить правильно знак заземления, убедиться: схема полностью тривиальна. В противном случае результаты заставят надолго поломать голову. Построение графиков Проиллюстрированный скрином фильтр верхних частот обнаруживает подъем амплитудно-частотной характеристики в районе 1 кГц. При нахождении полосы пропускания необходимо учесть: вертикальная шкала логарифмическая. Посему срез на уровне 70% максимума не соответствует семи десятым высоты пологой части пика. Заядлым любителям будет интересна фазочастотная характеристика, в окне расположенная снизу. Тот и другой график строятся из меню Analysis раздел AC Frequency. А еще тут… Fourier. Доступно посмотреть спектр выходного сигнала. В нашем случае не будет ничего интересного, поскольку собрали унылый пассивный фильтр, колебание на входе гармоническое. Гораздо интереснее наблюдать спектр импульсного сигнала. График отклика Раздел Transient показывает отклик на подачу фронта питающего напряжения. На графике фактически представлен процесс заряда батареи, откуда найдем постоянную времени по уровню 0,7 максимума. Тонкости понятны желающим собрать сглаживающий фильтр амплитудного детектора. Как видно из графика, значение составляет 250 мкс. Параметр определяется из окна следующим образом: По-другому постоянная времени вычисляется произведением сопротивления на общую емкость батареи. Пользуясь приведенными выше формулами, вычислим: С = 1 мкФ / 4 = 250 нФ. Осталось умножить значение на 1000 Ом, получится 250 мкс. Программный пакет Electronics Workbench 5.12 при умелом использовании высвобождает уйму свободного времени. Версия ПО В интернете бытует мнение: автором Electronics Workbench выступает дочерняя компания корпорации National Instruments, разрабатывающая программное обеспечение. Неправда. Из окна авторских прав упомянутого приложения видно: разработка выполнена отделом Interactive Image Technologies. Вышеозначенное подразделение обрело самостоятельность в 1995 году. Отдел направленно занимался рекламными и обучающими материалами. Electronics Workbench разработан для целей обучения студентов Канады. Потом программный продукт распространился всемирно, с некоторых пор именуется Multisim. Обновленный программный продукт продают официальные дилеры, перечень представлен официальным сайтом компании National Instruments: russia.ni.com/contact. На момент исследования счастливчиками, получившими право купить ПО не выезжая за город, назовем жителей Москвы, Санкт-Петербурга. Удачи решившимся связаться с официальными представителями, в Multisim добавлены новые фишки: vashtehnik.ru Ростовский государственный экономический университет (РИНХ) Елизаров Ю.Д Электротехника Методические указания по выполнению практических работ Ростов-на-Дону 2014 год Практическая работа №1 Электрические цепи постоянного тока Цель работы: -Исследование последовательного и параллельного соединения резисторов; -Эквивалентная замена двух последовательно включенных источников ЭДС; -Эквивалентная замена двух параллельно включенных источников ЭДС; -Исследование делителя напряжения; -Исследование делителя тока. Краткие сведения из теории Электрическая цепь обычно состоит из соединительных определенным образом элементов и соединительных проводников. Такими элементами могут быть сопротивления (резисторы), электрические емкости (конденсаторы), индуктивности (катушки индуктивности, реле, обмотки трансформатора и др.) В цепях переменного тока любой элемент цепи обладает сопротивлением, индуктивностью и емкостью, а в цепях постоянного тока имеет значение только сопротивление потребителя энергии, подводящих проводов и измерительных приборов. Поэтому электрическую цепь удобно представить схемой замещения, где каждый из элементов представлен своим сопротивлением. Закон Ома для замкнутой цепи I = Где I – сила тока в цепи, Е-ЭДС источника, R – сопротивление внешней цепи (нагрузки) и внутренней цепи источника. Напряжение на выходах источника U=E-IRвнутр. Эквивалентное преобразование участка цепи. Замена является эквивалентной, если ток через заменяемый участок цепи и напряжение на его выводах не изменяется при замене. Эквивалентная замена двух последовательно включенных сопротивлений одним Rэ: Rэ= Эквивалентная замена двух параллельно включенных сопротивлений одним Rэ: Rэ = Замена последовательно включенных источников ЭДС: Еэ =(сумма алгебраическая, учитывается знак ЭДС) Делители напряжения предназначены для уменьшения напряжения, подаваемого на участок цепи. Простейший делитель состоит их двух, соединённых последовательно, резисторов; выходное напряжение подают на оба резистора, выходное снимают с одного из них как показано на рисунке 1.1 Рис 1.1 Схема делителя напряжения Формула для вычисления снимаемого напряжения с плеча делителя U Такие делители используются, например, в приборах с несколькими диапазонами измерения. При измерении большего напряжения включается дополнительное сопротивление , а на показывающий прибор подается меньшее, пропорциональное подаваемому, напряжение. Делители тока предназначены для уменьшения тока в цепи. В этом случае два резистора включаются параллельно, и ток измеряется в цепи одного из них (рис 1.2) Так, например, осуществляется шунтирование в измерительных приборах приборов – амперметрах. Рис 1.2 Схема делителя тока Формула для вычисления тока через одно из плеч делителя тока (резистор R1) I = Порядок выполнения работы Изучить основные положения теорем электрических цепей постоянного тока. Рассчитать эквивалентное сопротивление участка электрической цепи из двух последовательно соединённых резисторов . Ознакомиться с вводной частью практикума по «Электротехника». Запустить программу. Найти в «Меню» «Правка» «Описание работ», открыть и выбрать лабораторную работу №1. Открыть файл c1_001 с электрической схемой. Включить мультиметр и измерить сопротивление с заданного участка цепи. Записать полученную величину и сравнить с рассчитанным значением сопротивления. Рассчитать эквивалентное сопротивление участка электрической цепи, состоящего из двух параллельно соединенных резисторов = 12 Ом Открыть файл c1_002. Включить мультиметр и измерить сопротивление заданного участка цепи. Записать полученную величину и сравнить с расчётным значение. Рассчитать значение эквивалентной ЭДС для последовательного соединения двух источников ЭДС . Отрыть файл с_003, подключить вольт метр к точкам А и В и проверить условие эквивалентности. Рассчитать напряжение на каждом резисторе делителя напряжения = 50 Ом = 100 Ом = 15 B Открыть файл с_007. Подключая вольтметр параллельно каждому резистору, проверить правильность расчета. Рассчитать токи через каждый резистор делителя тока - = 5 Ом= 10 ОмI = 6A Откройте файл с_008. Подключая амперметр последовательно с каждым резистором, проверить правильность расчетов. Оформить результат работы отчетом. Содержание отчета Название. Цель работы. Название эксперимента и исходные данные для расчета. Расчетные формулы, алгоритм вычислений и результаты расчета. Электрическая схема измерений для каждого эксперимента, результаты измерений. Выводы о соответствии расчетных и измерительных электрических величин по каждому эксперименту. Контрольные вопросы: Сформулируйте закон Ома для замкнутой цепи и для ее участка. В каких единицах выражают ЭДС, напряжение, силу тока, сопротивление. От чего зависит сопротивление однородного металлического проводника? Каково соотношения между ЭДС и напряжением на выводах источника электрической энергии? Как определяется ток при коротком замыкании выводов источника электрической энергии? Почему желательно, чтобы внутреннее сопротивление мощного источника электрической энергии было возможно меньшим? Сформулируйте первый и второй законы Кирхгофа, а также правило знаков для токов и ЭДС. Как определяется общее сопротивление при последовательном, параллельном и смешанном соединении потребителей энергии. Как определяется напряжение в делителе напряжения? Как определяется токи в делителе тока? Литература, пособия, инструкции: Касаткин А.С., Немцов М.В. «Электротехника». 2008 г, -522е. Синявский Г.П. и др. «Электротехника» Практикум РГЭУ(РИНХ) Ростов-на-Дону 2007г-76с. Практическая работа №2 Цепи однофазного синусоидального тока. Цель работы: Исследование амплитудно-фазовых соотношений и мощности для переменного тока и напряжения в резисторе, конденсаторе и катушке индуктивности. Краткие сведения из теории: Переменный ток промышленной частоты (f = 50 Гц) имеет синусоидальную форму i – мгновенное (в момент времени t) значение силы тока, Im – амплитуда (максимальное значение) тока, (wt – φi) где i - мгновенное (в момент времени t) значение силы тока, Im – амплитуда (максимальное значение) , (wt – φi) – фаза тока. В выражение для фазы тока входит w – циклическая частота переменного тока, связанные с обычной частатой соотношением w = 2 πf, а так же φ – начальная фаза (в момент времени t = 0). Соответственно и напряжение в цепи переменного тока имеет синусоидальную форму u = Um sin(wt+ φi), где все величины имеют аналогичный току смысл. Мгновения значения токаи напряжения можно определить амплитудные значения токаи напряжения. Обычно на практике ток и напряжение характеризуют их действующими значениями I и U, которые указывают в паспортах на приборы, на электрической арматуре и т.д. Действующие значения тока и амплитудными значениями соотношениями I = = 0,707 ; U == 0,707. В цепи переменного тока с резистором закон Ома выполняется как для амплитудных значений тока напряжения =R, так и для их действующих значений U = IR. Конденсатор в цепи переменного тока имеет емкостное сопротивление C – величина емкости конденсатора, ƒ – частота переменного тока. Мгновенные значение силы тока в конденсаторе i = (wt – φi), мгновенное значение напряжения на конденсаторе u = (wt – φi). Начальные фазы связаны соотношением =+ , то есть ток опережает по фазе напряжение на. Закон Ома связывает амплитудные значения тока и напряжения на конденсаторе соотношением=. Полная мощность двухполюсника определяется произведением действующих значений тока и напряжения (измеряется в ВА) S = =UI Связь полной, активной и реактивной мощностей =+Активную мощность измеряет ваттметрами разного принципа действия. Обычно ваттметр имеет две измерительные цепи, как показано на рис 2.1 рис 2.1 нагрузка Одна цепь ваттметра включена последовательно нагрузке, ток в ней i равен току нагрузки. Другая цепь включается параллельно и напряжение в ней равно напряжению u нагрузки. В лабораторной работе роль ваттметра выполняет умножитель напряжений. Порядок выполнения работы: Изучить основные положения теории электрических цепей однофазного синусоидального тока. Ознакомиться с вводной частью работы практикума «Электротехника» [2]. Запустить программу. Найти в меню «Правка» «Описание работ», открыть и выбрать лабораторную работу 2. Рассчитать действующее значение тока в резисторе, используя данные U = 120B, R = 120B, r = 0,01 Oм Открыть файл с2_01.ewb. Подключить амперметр и проверить правильность отчета. Определить фазовые соотношения тока и напряжения. (Есть ли фазовый сдвиг колебаний тока относительно колебаний подаваемого на резистор напряжения?) Подключить осциллограф и проверить соответствие теории данных эксперимента. Для этого измерить и сравнить периоды колебаний тока и напряжения на осциллограмме, а также сдвиг ∆T. Определить мощность резистора. Подать сигналы, пропорциональные току и цепи резистора (снимается в виде падения напряжения на вспомогательном резисторе 0,01 Ом) и напряжению на резисторе (снимается с источника ЭДС) на два входа умножителя. Подключить к выходу умножителя осциллограф в соответствие с электрической схемой рис. 2.1., по осциллограмме определить минимальную и максимальную активную мощность резистора. Подключив на выход умножителя вольтметр постоянного напряжения, убедиться, что с точностью до некоторого коэффициента он измеряет активную мощность. Определить на опыте этот коэффициент. u=120 B, f=50 Гц, с=53ϻФ, r=0,01 Oм 8. Открыть файл c2_02.ewb. Подключить амперметр и проверить правильность расчета. 9. Определить фазовые соотношения тока и напряжения на конденсаторе. (Совпадают ли по фазе колебания тока и напряжения в цепи конденсатора?) проверить экспериментально выводы теории. Подключить осциллограф, сравнить осциллограммы тока и напряжения, измерить периоды Т колебаний и сдвиг ∆T. Рассчитать фазовый сдвиг, зная, что периоду соответствует фаза 2π. Подать сигналы, пропорциональные току и напряжению, на два входа умножителя подключите на выход умножителя осциллограф. По осциллограмме мощности определить минимальные и максимальные значения реактивной мощности конденсатора. 11. Рассчитать действующую значение тока в катушке индуктивности по данным: u = 120В ƒ =5кГц L = 955,4 Мн r = 0,1Ом 12. Открыть файл с2_03.ewb. Подключить амперметр и проверить правильность расчета. 13. Определить фазовые соотношения тока и напряжения в цепи катушки индуктивности. Подключить осциллограф и проверить соответствие теории экспериментально наблюдаемых соотношений фаз тока и напряжения в цепи катушки индуктивности. 14. Измерение мощности катушки индуктивности. Подайте сигналы, пропорциональные току и напряжению, на два входа умножителя и по осциллограмме мощности. Определить минимальное и максимальное значения реактивной мощности катушки индуктивности. Содержание отчёта: 1.Название, цель работы. 2.Название эксперимента и исходные данные расчета. 3. Расчетные формулы, алгоритм вычислений для расчета. 4. Электрическая схема измерений для каждого эксперимента, результаты измерений. 5. Выводы с соответствием расчетных и измененных электрических величин, а также о соответствии результатов экспериментов теории. Контрольные вопросы: 1. Каковы основные характеристики синусоидального тока? 2. Какова связь между частотой, периодом и циклической частотой колебаний? 3. Какова связь между действующим, средним и амплитудным значениями синусоидального тока? 4. Как изображаются синусоидальные токи и напряжения с помощью вектора на комплексной плоскости? 5. Как сдвинуты друг относительно друга векторы тока и напряжения резистора, конденсатора, конденсатора, катушки индуктивности? 6. Как преобразуется электрическая энергия источника ЭДС в резисторе, конденсаторе и катушке индуктивности? Литература, пособия, инструкции: Касаткин А.С., Немцов М.В. «Электротехника». М.А. «Академия», -2008, 544е. Синявский Г.П. и др. «Электротехника» Практикум – РГЭУ(РИНХ) г. Ростов-на-Дону, 2007г.,-76с. Практическая работа №3 Цепи однофазного тока при последовательном включении электроприемников. Цель работы: Исследование физических процессов, происходящих в установившимся режиме в цепи, содержащий последовательно соединенные активное, индуктивное и емкостное сопротивление. Краткие сведения из теории. При последовательном включении элементов схемы силы тока в них одинакова по закону Ома для участка цепи, падение напряжения на резисторе, катушке индуктивности и конденсаторе соответственно пропорционально величине активного тока R, индуктивного Х. =(1) ==(2) Полное сопротивление цепи Z определяется по формуле: Z = (3) Действующие значение силы тока I, в цепи рассчитывается из выражения Z = (4) Где U-напряжение, снимаемое с источника ЭДС. Полная мощность, потребляемая цепью: = U; =Z, Коэффициент мощности можно определить как =, Цепь потребляет от источника активную мощность :=или=U Реактивная мощность равна разности индуктивной и емкостной мощностей: =-, Отметим здесь еще раз смысл коэффициента мощности. Коэффициент мощности равен: = Полную мощность S можно представить в виде S=, а для цепи содержащей конденсатор и катушку индуктивности,S=. Тогда для коэффициента мощностей такой цепи справедливо выражение = Таким образом, коэффициент мощности представляет собой величину, которая показывает долю активной мощности в общем балансе мощностей, потребляемых электроприемником. Из анализа последнего выражения можно сделать важные для теории и практики выводы: 1) Если реактивная мощность катушки больше реактивной мощности конденсатора, то цепь потребляет от источника и активную, и реактивную мощность; 2) Если реактивные мощности катушки больше реактивной мощности и конденсатора, то цепь потребляет от источника и активную, реактивную мощность; 3) Если реактивная мощность конденсатора больше реактивной мощности катушки, то цепь потребляет от источника активную мощность и отдает в сеть избыточную реактивную. Порядок выполнения работы: 1. Изучить основные положения теории электрических цепей однофазного синусоидального тока. 2. Ознакомиться с вводной частью практикума «Электротехника» [2]. Запустить программу. Найти в меню «Правка», «Описание работ», открыть и выбрать в папке Лаб 5 файл 51.ewb. 3. Рассчитать индуктивное, емкостное и полное сопротивление цепи (Ом), используя формулы (1,2,3), при U= 70, 71В., R=10 Ом, =50mГн, С=1mФ; 4. Рассчитать действующее значение силы тока в цепи и падение напряжения в резисторе , катушке индуктивностии конденсаторе. 5. Открыть файл 51.ewb в папке Лаб5. Измерить падение напряжения в резисторе, катушке индуктивности и конденсаторе. 6. Рассчитать катушки, потребляемые цепью: полную, активную и реактивную. Коэффициент катушки. 7. Оформить результаты работы отчетом. Содержание отчета: 1. Название, цель работы. 2. Исходные данные для расчета. 3. Расчетные формулы, алгоритм вычислений и результаты расчета. 4. Электрическая схема измерений, рисуемых осциллограммы напряжения сети и тока цепи, результаты измерений. 5. Выводы о соответствии расчетный и измерительных электрических величин. Контрольные вопросы: 1. Как изображается гармоническое колебание с помощью вектора? 2. Как сдвинуты друг относительно друга векторы тока и напряжения для резистора, конденсатора и катушки индуктивности? 3. Как строится векторная диаграмма для последовательного включённых R,L и С? 4. Что такое резонанс напряжений? 5. Какими мощностями характеризуются цепи синусоидального тока? 6. По каким формулам можно рассчитать полную, активную и реактивную мощности? 7. Как измерить активную мощность? 8. Что такое коэффициент мощности, каков смысл? Литература, пособия, инструкции: 1. Касаткин А.С., Немцов М.В. Электротехника. М: «Академия», 2008г-544с. 2.Синявский Г.П. и др. Электротехника: Практикум-РГЭУ(РИНХ) 2007г.-76с. Практическая работа №4 Цепи трехфазного тока при соединении электроприемников звездой. Цель работы: Исследование цепи трехфазного переменного тока в симметрическом режиме и влияния нейтрального провода на величину фазных напряжений электроприемников. Краткие сведения из теории В практике передачи и распределения электрической энергии соединяют в одну цепь три цепи синусоидального тока с независимыми источниками энергии. Источником электрической энергии служат три фазных обмотки статора трехфазного генератора переменного тока. При вращении магнитного поля ротора в этих обмотках последовательного тока. При вращении магнитного поля ротора в этих обмотках последовательно индуцируются синусоидальные ЭДС. Сдвинутые на фазный угол (треть периода) относительно друг друга. Цепь каждой обмотки генератора – фазным напряжением источника. Трехфазную систему получают, соединяя фазы источника энергии и приемники звездой или треугольником. При соединении звездой все концы фазных обмоток генератора соединяются в общий узел, концы фаз приемника тоже образуют узел, а три провода между ними объединяются в один общий нейтральный провод(нейтраль). Начала трех фаз генератора соединяются с фазами приемника тремя линейными проводами. Напряжение между линейными проводами называется линейным напряжением. Действующие значения линейных и фазных напряжений связаны с соотношением UЛ=2UФ*cos30=. Действующие линейные токи равны фазным. При симметричном режиме цепи, все напряжения источника равны между собой и одинаковы все три сопротивления электроприемника. При соединении в звезду фазные токи равны линейным, а линейные напряжения в раз больше фазных: ==. Когда электроприемник представляет собой активную нагрузку, то угол сдвига между токами и напряжениями каждой фазной цепи равен 0, а полная мощность электроприемника равна активной, которая складывается из активных мощностей фаз, Вт: S=P=3=3R. В общем случае трехфазный электроприемник потребляет от источника активную и реактивную мощность. Рассчитываются активные мощности каждой фазы, Вт: = cos φ, = cosφ, = cosφ, Активная мощность электроприемника: Р=++; при симметрии Р=3. Рассчитываются реактивные мощности каждой фазы,, вар: = φ, = φ, = φ, Q = . при симметрииQ = 3. Коэффициент мощности можно определить: == Полная мощность электроприемника, В*А, S= Порядок выполнения работы 1. Изучить основные положения теории электрических цепей трехфазного тока. 2. Ознакомиться с вводной частью практикума «Электротехника» [2]. Запустить программу. Найти в меню « Правка» - «Описание работ», открыть и выбрать в папке Лаб8 фаул81.ewb. 3. Рассчитать фазные токи и напряжение в симметрическом режиме, при =50Гц,=100 Ом,=100 Ом,=100 Ом. 4. Открыть файл 81.ewb в папке Лаб8. Измерить замещение фазных токов и напряжений тока, в контрольном проводе. Изменить характер осциллограмм фазных напряжений. 5. Рассчитать активную, реактивную и полную мощность трехфазной цепи. 6. Оформить результаты работы отчетом. Содержание отчета: 1. Название, цель работы. 2. Исходные данные для расчета. 3. Расчетные формулы, алгоритм вычислений и результаты расчета. 4.Электрическая схема измерений, рисунок осциллограмм фазных напряжений, результаты измерений. 5. Выводы о соответствии расчетных и измеримых электрических величин. Контрольные вопросы 1. Что такое трехфазный переменный ток и почему он так называется? 2. Что называется фазой цепи трехфазного тока? 3. Какое соединение обмоток генератора называется соединением «звездой»? 4. При каких условиях можно производить соединение фаз «звездой» без нулевого провода? 5. Что называется линейным напряжением и фазовым напряжением? 6. Каково соотношение между фазовым и линейным напряжениями при соединении «звездой»? 7. К чему приведет обрыв нулевого провода при несимметричной нагрузке? 8. Как измеряют мощность и энергию трехфазной системы при симметричной и несимметричной нагрузках? Литература, пособия, инструкции: 1. Касаткин А.С., Немцов М.В. Электротехника. М. «Академия»,-2008-544с. 2.Синяковский Г.П. и др. Электротехника: Практикум – РГЭУ(РИНХ) 2007г.76с. studfiles.netКонденсатор в цепи переменного тока. Емкостное сопротивление конденсатора. Формула напряжение на конденсаторе
Последовательное соединение конденсаторов: формула :: SYL.ru
Что необходимо знать для правильного соединения?
Зачем так делают?
Что ещё необходимо знать, чтобы правильно соединить конденсаторы?
Ток при последовательном соединении
Падение напряженности и общая емкость
Пример № 1
Пример № 2
Заключение
Способы подключения конденсаторов в электрическую цепь
Параллельное включение конденсаторов в цепь
 Параллельное соединение конденсаторов
Параллельное соединение конденсаторов  Формула и расшифровка
Формула и расшифровка Формула
ФормулаПоследовательное включение конденсаторов в цепь
 Формула
Формула Последовательное соединение конденсаторов
Последовательное соединение конденсаторов Основные моменты
Основные моменты Формула
Формула Формула
ФормулаСмешанное включение емкостных накопителей в схему
 Схема подключения конденсаторов
Схема подключения конденсаторов Последовательное, параллельное и смешанное соединение конденсаторов
Последовательное, параллельное и смешанное соединение конденсаторовВывод
Конденсатор в цепи переменного тока

Емкостное сопротивление конденсатора


Похожие материалы:
Добавить комментарий
ЛР 3.3. Заряд разряд конденсатора
Параллельное соединение конденсаторов формула - Всё о электрике в доме
Последовательное и параллельное соединение конденсаторов

 Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:
Если в цепи имеются всего лишь два последовательно соединенных конденсатора, то общая емкость определяется по формуле:
 Так при параллельном соединении, емкости всех конденсаторов складываются:
Так при параллельном соединении, емкости всех конденсаторов складываются: То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором.
То есть, емкость каждого конденсатора, включенного параллельно суммируется и получается одна большая емкость, которую можно на схеме представить одним конденсатором. И представляет с собой различные сочетания параллельного и последовательного соединений.Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.Например, дана следующая схема и следующие данные:
И представляет с собой различные сочетания параллельного и последовательного соединений.Для вычисления общей емкости таких соединений, применяют метод замещения: все конденсаторы делят на последовательно и параллельно соединенные группы, рассчитывают ёмкость каждой группы в отдельности, так что в конце выйдет две параллельных или последовательных емкостей, которые можно без труда посчитать.Например, дана следующая схема и следующие данные: C1=0.4ФC2=0.8ФC3=0,73ФНеобходимо найти общую емкость всех трех конденсаторов.Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.
C1=0.4ФC2=0.8ФC3=0,73ФНеобходимо найти общую емкость всех трех конденсаторов.Как мы видим конденсаторы C1 и C2 соединены последовательно, а конденсатор C3 по отношению к первым двум параллельно.Посчитав общую емкость последовательно соединенных конденсаторов C1 и C2, их можно представить, как один конденсатор C1,2.
 Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.
Теперь нам не составит труда посчитать емкость двух параллельно соединенных конденсаторов, просто сложив их ёмкости.

Схемы соединения конденсаторов: параллельное, последовательное
Параллельное соединение конденсаторов
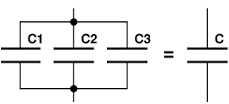
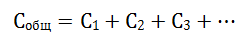
Последовательное соединение конденсаторов
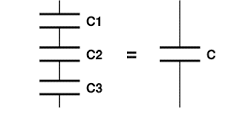
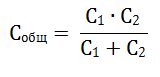
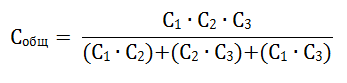
Смешанное соединение конденсаторов
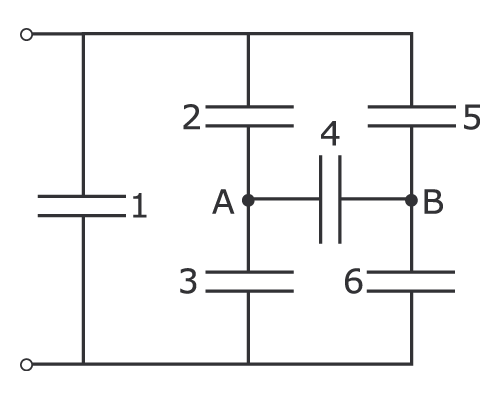
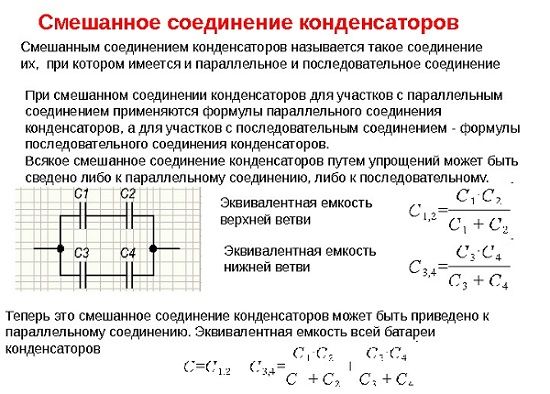
Соединение конденсаторов
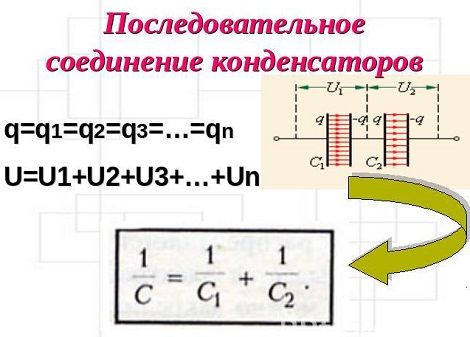
Последовательное соединение

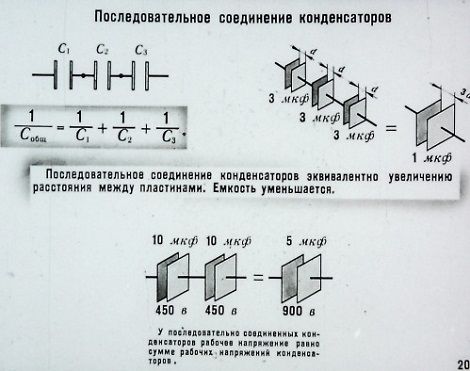
Смешанное соединение
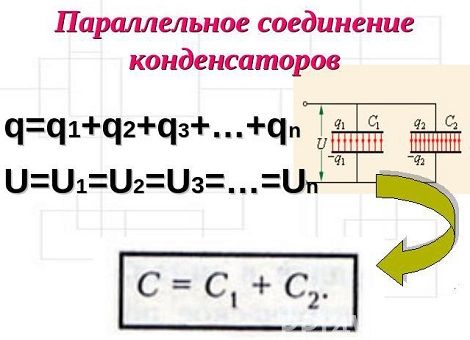
Параллельное соединение конденсаторов
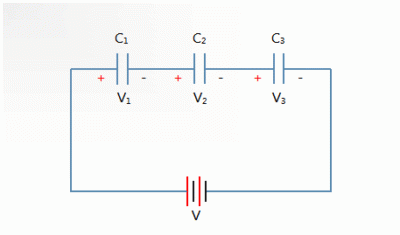
Последовательное соединение конденсаторов: особенности и примеры
Физические процессы при последовательном соединении
Вычисление общей емкости батареи
Необходимость в последовательном соединении
Программные пакеты исследования электрических цепей
Рабочий пример
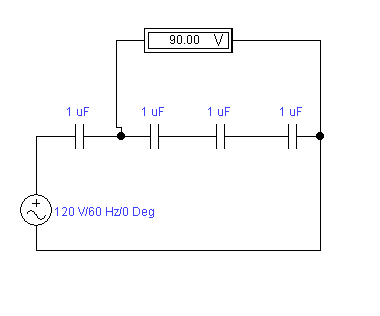
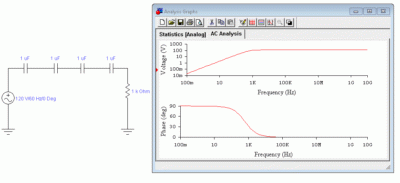
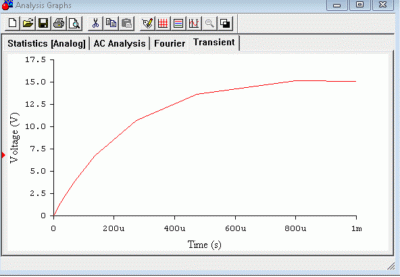

Раздобыть программный пакет расчета электрики
7. Рассчитать действующие значения силы тока в конденсаторе, используя данные;
10. Измерить мощность конденсатора.
15. Оформить результаты работы отчётом.
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''











Поделиться с друзьями: