В современных системах передачи электрической энергии на дальние расстояния, электроснабжения и распределения электрической энергии применяются трехфазные цепи, которые по сравнению с однофазными имеют значительные преимущества: Меньший расход проводникового материала, меньшая стоимость и более высокая экономичность линии электропередачи при одинаковой мощности и напряжении ЛЭП. Возможность получения двух эксплуатационных напряжений (линейного и фазного) в одной трёхфазной четырёхпроводной системе. Возможность простого получения вращающегося магнитного поля (ВМП), на использовании которого основана работа самых распространённых потребителей электрической энергии - трёхфазных асинхронных и синхронных электродвигателей. Мощность трехфазной цепи – это сумма соответствующих мощностей всех трех фаз (потерями мощности в нейтральном проводе обычно пренебрегают): Как и в однофазной цепи активная, реактивная и полная мощности трёхфазной цепи связаны соотношением: . Мощность любой из фаз выражается обычной формулой: . В случае симметричной нагрузки мощности всех трёх фаз соответственно равны: и для мощности трёхфазной цепи можно записать: . В трёхфазной цепи при симметричной нагрузке: , поэтому для мощности трёхфазной цепи можно записать: Кроме того, при симметричной нагрузке известны соотношения между линейными и фазными напряжениями и токами: I Л = I Ф , U Л U Ф - при соединении по схеме «звезда», I Л I Ф , U Л = U Ф - при соединении по схеме «треугольник». После подстановки этих выражений в формулу мощности трёхфазной цепи в общем случае при симметричной нагрузке получаем: . В случае несимметричной нагрузки мощность трёхфазной цепи следует находить как сумму соответствующих мощностей всех трёх фаз (т.е. как сумму соответствующих фазных мощностей): Измерение активной мощности трёхфазной цепи Активная мощность в цепи переменного тока P = I U cos φ измеряется с помощью электродинамического ваттметра, измерительный механизм которого состоит из двух катушек, одна из которых может вращаться. Обмотка неподвижной катушки – последовательная или токовая обмотка – обладает малым сопротивлением и включается в измеряемую цепь последовательно, а обмотка подвижной катушки - обмотка напряжения - имеет большое сопротивление и включается параллельно на зажимы нагрузки (потребителя). где k - конструкционный коэффициент, I - ток в последовательной обмотке ваттметра. При включении ваттметра в цепь следует обращать внимание на правильное подключение обмоток ваттметра, начала которых ( генераторные зажимы) обозначаются звёздочками (* ). Оба генераторных зажима должны быть присоединены к одному и тому же проводу со стороны источника электрической энергии (генератора). Для измерения активной мощности трёхфазной цепи часто используется однофазный ваттметр активной мощности, включаемый по различным схемам. Измерение активной мощности методом одного ваттметра Метод одного ваттметра применяется в трёхфазных цепях только при симметричной нагрузке фаз. При симметричной нагрузке мощность, потребляемая каждой из трёх фаз, одинакова, поэтому достаточно измерить мощность одной фазы и, умножив результат измерения на число фаз, получить мощность трёхфазной цепи: . Следовательно, для измерения мощности при симметричной нагрузке достаточно одного ваттметра, токовая обмотка которого включается последовательно с фазной нагрузкой, а обмотка напряжения – включается на фазное напряжение. Если нейтральная точка нагрузки недоступна, то измерение фазной мощности в соединении звезда выполняют по схеме с искусственной нейтральной точкой, созданной соединёнными в звезду обмоткой напряжения ваттметра Z Vи двух равных ей по сопротивлению добавочных резисторов Z 2 и Z 3 : . studfiles.net 1. При расчете трехфазных цепей исходят из предположения, что генератор дает симметричную систему напряжений. На практике несимметрия нагрузки практически не влияет на систему напряжений генератора в том случае, если мощность нагрузки мала по сравнению с мощностью генератора или сети электроснабжения. 2. Схема соединения обмоток трехфазного генератора не предопределяет схему соединения нагрузки. Так, при соединении фаз генератора в звезду нагрузка может быть соединена в звезду с нейтральным проводом, в звезду без нейтрального провода или, наконец, в треугольник. В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей. Соединение потребителей звездой В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз (3.23) P = Pa + Pb + Pc, где (3.24) Pa = Ua Ia cos φa; Pb = Ub Ib cos φb; Pc = Uc Ic cos φc; Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токи; φa, φb, φc – углы сдвига фаз между напряжением и током. Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз (3.25) Q = Qa + Qb + Qc, где (3.26) Qa = Ua Ia sin φa; Qb = Ub Ib sin φb; Qc = Uc Ic sin φc. Полная мощность отдельных фаз (3.27) Sa = Ua Ia; Sb = Ub Ib; Sc = Uc Ic. Полная мощность трехфазного приемника (3.28) . При симметричной системе напряжений (Ua = Ub = Uc = UФ) и симметричной нагрузке (Ia = Ib = Ic = IФ; φa = φb = φc = φ) фазные мощности равны Pa = Pb = Pc = PФ = UФ IФ cos φ; Qa = Qb = Qc = QФ = UФ IФ sin φ. Активная мощность симметричного трехфазного приемника (3.29) P = 3 PФ = 3 UФ IФ cos φ. Аналогично выражается и реактивная мощность (3.30) Q = 3 QФ = 3 UФ IФ sin φ. Полная мощность (3.31) S = 3 SФ = 3 UФ IФ. Отсюда следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат. Соединение потребителей треугольником В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз (3.32) P = Pab + Pbc + Pca, где (3.33) Pab = Uab Iab cos φab; Pbc = Ubc Ibc cos φbc; Pca = Uca Ica cos φca; Uab, Ubc, Uca; Iab, Ibc, Ica – фазные напряжения и токи; φab, φbc, φca – углы сдвига фаз между напряжением и током. Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз (3.34) Q = Qab + Qbc + Qca, где (3.35) Qab = Uab Iab sin φab; Qbc = Ubc Ibc sin φbc; Qca = Uca Ica sin φca. Полная мощность отдельных фаз (3.36) Sab = Uab Iab; Sbc = Ubc Ibc; Sca = Uca Ica. Полная мощность трехфазного приемника (3.37) . При симметричной системе напряжений (Uab = Ubc = Uca = UФ) и симметричной нагрузке (Iab = Ibc = Ica = IФ; φab = φbc = φca = φ) фазные мощности равны Pab = Pbc = Pca = PФ = UФ IФ cos φ; Qab = Qbc = Qca = QФ = UФ IФ sin φ. Активная мощность симметричного трехфазного приемника P = 3 PФ = 3 UФ IФ cos φ. Аналогично выражается и реактивная мощность Q = 3 QФ = 3 UФ IФ sin φ. Полная мощность S = 3 SФ = 3 UФ IФ. Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через линейные величины UЛ и IЛ. При соединении фаз симметричного приемника звездой UФ = UЛ / , IФ = IЛ, при соединении треугольником UФ = UЛ, IФ = IЛ / . Поэтому независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой (3.38) P = UЛ IЛ cos φ. где UЛ и IЛ – линейное напряжение и ток; cos φ – фазный. Обычно индексы "л" и "ф" не указывают и формула принимает вид (3.39) P = U I cos φ. Соответственно реактивная мощность (3.40) Q = U I sin φ. и полная мощность (3.41) S = U I. При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током, и, что при неизмененном линейном напряжении, переключая приемник со звезды в треугольник его мощность увеличивается в три раза: Δ P = Υ 3P. Измерение активной мощности в трехфазных цепях Измерение активной мощности в трехфазных цепях производят с помощью трех, двух или одного ваттметров, используя различные схемы их включения. Схема включения ваттметров для измерения активной мощности определяется схемой сети (трех- или четырехпроводная), схемой соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная), доступностью нейтральной точки. При несимметричной нагрузке в четырехпроводной цепи активную мощность измеряют тремя ваттметрами (рис. 3.18), каждый из которых измеряет мощность одной фазы – фазную мощность. Рис. 3.18 Активная мощность приемника определяют по сумме показаний трех ваттметров (3.42) P = P1 + P2 + P3, где P1 = UA IA cos φA; P2 = UB IB cos φB; P3 = UC IC cos φC. Измерение мощности тремя ваттметрами возможно при любых условиях. При симметричном приемнике и доступной нейтральной точке активную мощность приемника определяют с помощью одного ваттметра, измеряя активную мощность одной фазы PФ по схеме рис. 3.19. Активная мощность всего трехфазного приемника равна при этом утроенному показанию ваттметра: P = 3 PФ. Рис. 3.19 Рис. 3.20 На рис. 3.19 показано включение прибора непосредственно в одну из фаз приемника. В случае, если нейтральная точка приемника недоступна или зажимы фаз приемника, включенного треугольником не выведены, применяют схему рис. 3.20 с использованием искусственной нейтральной точки n'. В этой схеме дополнительно в две фазы включают резисторы с сопротивлением R = RV. Измерение активной мощности симметричного приемника в трехфазной цепи одним ваттметром применяют только при полной гарантии симметричности трехфазной системы. Измерение активной мощности двумя ваттметрами В трехпроводных трехфазных цепях при симметричной и несимметричной нагрузках и любом способе соединения приемников широко распространена схема измерения активной мощности приемника двумя ваттметрами (рис. 3.21). Показания двух ваттметров при определенной схеме их включения позволяют определить активную мощность трехфазного приемника, включенного в цепь с симметричным напряжением источника питания. На рис. 3.21 показана одна из возможных схем включения ваттметров: здесь токовые катушки включены в линейные провода с токами IA и IB, а катушки напряжения – соответственно на линейные напряжения UAC и UBC. Рис. 3.21 Докажем, что сумма показаний ваттметров, включенных по схеме рис. 3.21, равна активной мощности Р трехфазного приемника. Мгновенное значение общей мощности трехфазного приемника, соединенного звездой, (3.43) p = uA iA + uB iB + uC iC. Так как (3.44) iA + iB + iC = 0. то (3.45) iC = -(iA + iB). Подставляя значение iC в выражение для р, получаем (3.46) p = uA iA + uB iB - uC (iA + iB) = (uA - uC) iA + (uB - uC) iB = uAC iA + uBC iB. Выразив мгновенные значения u и i через их амплитуды, можно найти среднюю (активную) мощность (3.47) , которая составит (3.48) P = UAC IA cos(UAC^IA) + UBC IB cos(UBC^IB) = P1 + P2. Так как UAC, UBC, IA и IB – соответственно линейные напряжения и токи, то полученное выражение справедливо и при соединении потребителей треугольником. Следовательно, сумма показаний двух ваттметров действительно равна активной мощности Р трехфазного приемника. При симметричной нагрузке IA = IB = IЛ, UAC = UBC = UЛ. Рис. 3.22 Из векторной диаграммы (рис. 3.22) получаем, что угол α между векторами UAC и IA равен α = φ - 30°, а угол β между векторами UBC и IB составляет β = φ + 30°. В рассматриваемом случае показания ваттметров можно выразить формулами (3.49) P1 = UЛ IЛ cos(φ - 30°), (3.50) P2 = UЛ IЛ cos(φ + 30°). Сумма показаний ваттметров (3.51) P1 + P2 = UЛ IЛ [cos(φ - 30°) + cos(φ + 30°)] = UЛ IЛ cos φ. Ввиду того, что косинусы углов в полученной формуле могут быть как положительными, так и отрицательными, в общем случае активная мощность приемника, измеренная по методу двух ваттметров, равна алгебраической сумме показаний. При симметричном приемнике показания ваттметров Р1 и Р2 будут равны только при φ = 0°. Если φ > 60°, то показания второго ваттметра Р2 будет отрицательным. Для измерения активной мощности в трехфазных цепях промышленных установок широкое применение находят двухэлементные трехфазные электродинамические и ферродинамические ваттметры, которые содержат в одном корпусе два измерительных механизма и общую подвижную часть. Катушки обоих механизмов соединены между собой по схемам, соответствующим рассмотренному методу двух ваттметров. Показание двухэлементного ваттметра равно активной мощности трехфазного приемника. Лицензия Model.Exponenta.Ru Jigrein © Н.В. Клиначёв, 1999-2008. Все права защищены. 800x600. studfiles.net -17- Магнитное поле определяется как одна из двух сторон электромагнитного поля, характеризующаяся воздействием на движущиеся заряженные частицы, магниты и пр. Интенсивность магнитного поля характеризуется двумя величинами: напряженностью магнитного поля и вектором магнитной индукции. Первая не зависит, а вторая зависит от свойств окружающей среды: B=μ0 μ H , где B — вектор магнитной индукции, H – напряженность магнитного поля, μ0 =4π*10-7 Гн/м — абсолютная магнитная проницаемость, μ — относительная магнитная проницаемость. В зависимости от величины μ все вещества делятся на три группы: диамагнетики (μ<1), парамагнетики (μ>1) и ферромагнетики (μ>>1). Магнитной цепью называется совокупность устройств, содержащих ферромагнитные вещества. Процессы в магнитных цепях описываются с помощью понятий магнитодвижущей силы (МДС), магнитного потока. Магнитным потоком Ф называется поток вектора магнитной индукции B через поверхность S: , где α — угол между векторами B и S. Магнитный поток Φ =∫B dS=B Scosα S измеряется в веберах (Вб). Теория всех электромагнитных явлений базируется на двух основных законах: законе электромагнитной индукции изаконе полного тока. Закон электромагнитной индукции гласит: ЭДС, индуктированная через поверхность, ограниченную контуром цепи, равна скорости изменения магнитного потока, взятой с обратным знаком. Закон полного тока гласит: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Он выражается формулой: n , где H – вектор напряженности магнитного поля, dl – вектор Φ = H dl=∑ik k=1 бесконечно малого элемента контура, по которому осуществляется обход; i k – токи, пронизывающие контур. В общем случае, полный ток складывается из токов проводимости, переноса и смещения (возникающие при изменениях электрического поля). Знаки токов определяются по правило правого винта. Источником МДС является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током). МДС электромагнита: Φ=I W , где I – полный ток, W – число витков катушки. Вмагнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности. Рассмотрим расчет магнитной цепи, изображенной на рис. 9.2. Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S. lср - длина средней силовой линии магнитного поля в магнитопроводе; δ - толщина воздушного зазора. На магнитопроводе размещена обмотка, по которой протекает ток I. Прямая задача расчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу studfiles.net Измерение активной мощности в трехфазных цепях Для трехпроводной трехфазной цени полную комплексную мощность несимметричной нагрузки можно выразить через фазные напряжения и фазные токя нагрузки соотношени (9.4) Действительная часть соотношения (9.4)представляет активную мощность (9.5) а мнимая часть — реактивную мощность где - угол .между фазным током и фазным напряжением рассматриваемой фазы. Для симметричной ,нагрузки поэтому и Если симметричная нагрузка соединена звездой, то линейное напряжение на нагрузке будет в раз больше фазного, а линейный токбудет равен фазному теку, тогда Если симметричная нагрузка соединена треугольником, то линейное напряжение на нагрузке равно фазному, а линейный токв раз больше фазного, тогда Отсюда следует, что для симметричной нагрузки при любом способе соединения ее сопротивлений активная мощность трех фаз будет ( 9.6 ) ' где Uи I -линейное напряжение и линейный ток, а - угол между фазными током и напряжением. По аналогии с (9.6)реактивная мощность симметричной трехфазной нагрузки будет Модуль полной мощности найдем через РиQ Комплексная мощность трех фаз симметричной нагрузки 'Активная мощность трехпроводной трехфазной цепи с несимметричной нагрузкой может быть измерена, как это следует из (9.5), при помощи трех ваттметров, включенных в фазы нагрузки. Однако, если учесть, что ито из (9.4)путем исключения одного из токов, например тока, получим Действительная часть этого выражения есть активная мощность несимметричной трехфазной нагрузки, поэтому эту мощность можно измерить с помощью двух ваттметров, включенныхв линию как показано на рис. 9.40.Суммарная мощность при этом Рис. 9.40 будет равна алгебраической сумме показаний двух ваттметров, т. е. так как показание одного из двух ваттметров может быть и отрицательным. Активная мощность четырехпроводной трехфазной цепи с несимметричной нагрузкой может быть измерена с помощью трех ваттметров, включенных по схеме рис. 9.41.При этом у всех приемников сопротивления должны, быть соединены звездой с нулевым проводом. При симметричной нагрузке активную мощность трехфазной трехпроводной цепи можно измерить одним ваттметром, включенным в фазу нагрузки, утроив его показание. Если Рис. 9.41 нагрузка недоступна, то измерение суммарной активной мощности можно осуществить двумя ваттметрами посхеме рис. 9.40,либо по схеме с искусственной нулевой точкой, приведенной на рис. 9.42.Искусственная нулевая точка создается из трех одинаковых сопротивлений. Суммарная активная мощность в этом случае равна утроенному показанию ваттметра. Рис. 9.42 Рис. 9.43 Пример 9.9.Определить показания ваттметров в схеме рис. 9.43,включенных для измерения суммарной активной мощности несимметричной трехфазной нагрузки приUAB=220В, rAB= 11Ом,rBC=rCA=22 Ом. Решение Показание ваттметра и фазе А: показание ваттметра в фазе В :Отсюда следует, что надо найти линейные токиии углы между напряжением и токоми между напряжениеми током . Принимаем , тогда: ; ; , и ; Так как , тои угол междуибудетУгол междуибудет Вычисляем Суммарная мощность будет. Для проверки найдем суммарную мощность как ,т. е. studfiles.net Так как в схеме есть нейтральный провод, то напряжение на фазах нагрузки равно соответствующему фазному напряжению источника питания (обмотки генератора считаем соединенными звездой, а сопротивлением нейтрального провода пренебрегаем): Рисунок 9 – Схема трёхфазной цепи при соединении потребителей звездой , , ; в численном виде: ω = 2πf = 2 ∙ 3,14 ∙ 50 = 314 1/с . Реактивное индуктивное сопротивление xL3 = ω L3 = 314 ∙ 31,8 ∙ 10–3 = 10 Ом. Реактивное емкостное сопротивление xС2 =1/(ω С2) = 1/(314 ∙ 159 ∙ 10–6) = 20 Ом. В общем случае полное сопротивление каждой из фаз в комплексной форме определяют с помощью выражения, которое использовалось в однофазных цепях, . Применяем эту формулу для нашего конкретного случая и получаем полные сопротивления фаз в следующем виде: Комплексные сопротивления фаз различны, следовательно, нагрузка несимметричная. Токи в линейных проводах (фазные токи нагрузки) определяем с помощью закона Ома: Ток в нейтральном проводе находим по первому закону Кирхгофа Полные мощности фаз: Так как вещественная часть полной мощности есть активная мощность цепи, а мнимая часть – реактивная, то, просуммировав отдельно вещественные, а затем мнимые части мощностей трех фаз, определяем трехфазную активную и реактивную мощности. Активная трехфазная мощность нагрузки может быть определена суммой активных мощностей потребителей каждой из фаз Относительная ошибка вычислений для активной мощности Реактивная трехфазная мощность нагрузки также определяется суммой реактивных мощностей потребителей каждой из фаз Относительная ошибка вычислений для активной мощности Ошибка менее одного процента допускается. Таким образом, баланс активных и реактивных мощностей соблюдается, значит токи определены правильно. Векторную диаграмму размещаем на комплексной плоскости с осями +1 и + j, рисунок 3.21. Выбираем масштаб векторов тока равным 10 А/деление, а векторов напряжения – 40 В/деление. Строим векторы фазных напряжений, а затем векторы токов. Длина вектора соответствует в масштабе модулю показательной формы соответствующего выражения тока или напряжения, а угол, под которым этот вектор строится к вещественной оси, равен аргументу комплексного значения величины. Рисунок 10 – Векторная диаграмма при соединении потребителей звездой с нейтральным проводомМощность трехфазной цепи калькулятор. Расчёт трёхфазных цепей. Мощность трехфазной цепи
17. Преимущества трехфазных систем. Мощность в трехфазной цепи. Способы измерения активной и реактивной мощности в трехфазных цепях.
Мощность трехфазной цепи
Общие замечания к расчету трехфазных цепей
Мощность трехфазной цепи, ее расчет и измерение
15. Мощность трехфазной электрической цепи.
19.Основные понятия о магнитных цепях и методах их расчета.
20.Магнитные цепи с постоянной магнитодвижущей силой.
9.5. Мощность трехфазной цепи.
1. Расчет трехфазной цепи при соединении потребителей звездой.
Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту
Активная трехфазная мощность
Реактивная трехфазная мощность
Полная мощность
Суммарная реактивная мощность всех потребителей
2. Расчёт трёхфазной цепи при соединении потребителей треугольником.
Нарисуем схему трёхфазной цепи, причем элементы из фазы A, B, C соединения потребителей звездой подключим соответственно между точками ab, bc, ca при соединении потребителей треугольником (рисунок 11).
В комплексной форме записи линейные напряжения на нагрузке:
Рисунок 11 – Схема трёхфазной цепи при соединении потребителей
треугольником
Сопротивления фаз нагрузки в комплексной форме:
Фазные токи определяем по закону Ома:
Для определения линейных токов используем первый закон Кирхгофа для точек a,в,cсхемы (рисунок 11)
А,
А,
А.
Полные комплексные мощности
Трехфазная активная мощность
Вт.
Трехфазная реактивная мощность
Трехфазная полная мощность
Векторную диаграмму токов для нагрузки, соединенной треугольником,строим в масштабе на комплексной плоскости относительно осей +1 и + j (рисунок12).На векторной диаграмме линейные токи получены на основании первого закона Кирхгофа, путем вычитания одного вектора фазного тока из соответствующего другого.
Рисунок 12 – Векторная диаграмма токов для
нагрузки, соединённой треугольником
ЗАДАЧА 1
РАСЧЕТ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПОСТОЯННОГО ТОКА
Для цепи, изображенной на рисунке 13, известны ЭДС Е1, Е2 и внутренние сопротивления r01, r02 источников питания, а также сопротивления r1–r6. Необходимо:
1. Составить систему уравнений для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
2. Определить токи ветвей методом контурных токов.
3. Составить баланс мощностей.
4. Построить потенциальную диаграмму для контура, включающего две ЭДС.
Значения параметров элементов цепи приведены в таблице 1. Теоретический материал и пример расчета даны во втором разделе пособия, а также в учебниках [1 – 4, 10].
Таблица 1 – Числовые значения исходных данных к задаче № 3
| Вариант | E1 | E2 | r01 | r02 | r1 | r2 | r3 | r4 | r5 | r6 |
| B | Ом | |||||||||
| 1 2 3 4 5 6 7 8 9 0 | 27 12 127 127 36 220 127 220 127 36 | 12 127 110 12 127 36 220 380 36 220 | 0,1 0,3 0,1 0,4 0,5 0,3 0,6 0,5 0,7 1,8 | 0,8 0,6 1,0 1,2 0,7 0,8 1,2 1,5 1,2 2,8 | 5 3 9 4 6 6 7 9 5 9 | 3 8 4 7 3 8 4 3 3 6 | 7 5 5 2 9 3 1 6 7 3 | 6 3 5 2 3 6 2 5 5 8 | 3 4 6 4 5 4 5 3 8 6 | 7 5 7 5 3 6 8 8 9 3 |
Рисунок 13 – Варианты электрических цепей к задаче № 1
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
Продолжение рисунка 13
studfiles.net
Мощность трехфазной цепи калькулятор. Расчёт трёхфазных цепей
6. Расчёт трёхфазных цепей.
Многофазной системой электрических цепей называют совокупность электрических цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе, создаваемые общими источником энергии (ГОСТ 19880-74).
Многофазной цепью называют многофазную систему электрических цепей в которой отдельные фазы электрически соединены друг с другом (ГОСТ 19880-74). В частности при числе фаз многофазной системы равной 3 будем иметь трехфазную цепь.
Различают симметричную и несимметричную многофазную систему. Симметричной многофазной системой токов называют мно гофазную систему электрических токов в которой отдельные электрические токи равны по амплитуде и отстают по фазе относительно друг друга на уг л ы равные , где m – число фаз. (ГОСТ 19880-74).
Несимметричной многофазной систем ой электрических токов называ ют систему не удовлетворяющую любому из вышеуказанных признаков (ГОСТ 19880-74).
6.1. Трехфазная система ЭДС.
Под трёхфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе относительно друг друга на 120°.
,
,
.
Соответственно, для действующих ЭДС в комплексной форме можно записать
,
,
и изобразить на комплексной плоскости
6.2. Общие положения и допущения при расчете трехфазных цепей.
Трехфазные цепи являются разновидностью цепей синусоидального тока и поэтому их расчет производится теми же методами и приёмами, которые присущи цепям однофазного синусоидального тока. Для анализа трехфазных цепей применим комплексный (символический) метод расчета, могут строиться векторные и топографические диаграммы.
Для анализа трехфазных цепей введем два допущения, которые сводятся к тому, что синусоидальное напряжение на зажимах трехфазного генератора симметричны при любой нагрузке:
система ЭДС трехфазного генератора, симметрична;
все источники ЭДС имеют бесконечно большую мощность.
6.3.Расчет соединения звезда-звезда с нулевым проводом.
П
редположим сейчас и в дальнейшем, что сопротивление проводов, соединяющих источник с нагрузкой, равно нулю. В этом случае в схеме образуются три обособленных контура. Токи в них
,
,
,
где ,и- линейные токи, а,и- фазные токи, токи в нагрузке, соответственно, фазыa, b, c.
Ток в нулевом проводе равен
. Напряжение между линейным проводом и нулевым узлом
- фазное напряжение:
,и. Напряжение между линейными проводами
- линейное напряжение:
,
и
.
При соединении звезда-звезда с нулевым проводом, справедливы следующие соотношения для токов:
,
и
; или для модулей:
; для напряжений:
,
,
и
,
,
; или для модулей:
.
С
имметричная многофазная (трёхфазная) цепь – это цепь, в которой комплексные сопротивления, составляющих её фаз, одинаковы (ГОСТ 19880-74). На рисунке представлена векторная диаграмма напряжений на источнике и нагрузке. Векторная диаграмма токов построена для симметричной цепи ак-тивного характера. При этом
и, следовательно, нулевой провод может быть устранён из цепи без изме-нения режима её работы. Аннало-гичная ситуация наблюдается и для симметрич-ной цепи с ак-тивно-реактивной нагрузкой, когда
.
Если нагрузка несимметрич
levevg.ru
Электротехника. Трехфазные электрические цепи
Федеральное агентство по образованию ГОУ ВПО "Уральский государственный технический университет – УПИ"
Электротехника: Трехфазные электрические цепи
Учебное пособие
В.С. Проскуряков, С.В. Соболев, Н.В. Хрулькова Кафедра "Электротехника и электротехнологические системы"
Екатеринбург 2007
2
Оглавление
1.Основные понятия и определения
2.Получение трехфазной системы ЭДС.
3.Способы соединения фаз в трехфазной цепи.
4.Напряжения трехфазного источника.
5.Классификация приемников в трехфазной цепи.
6.Расчет трехфазной цепи при соединении фаз приемника «Звездой»
7.Значение нейтрального провода
8.Расчет трехфазной цепи при соединении фаз приемника «треугольником»
9.Мощность трехфазной цепи
3
Трехфазные электрические цепи.
1. Основные понятия и определения
Трехфазная цепь – это совокупность трех электрических цепей, в которых
действуют синусоидальные ЭДС, одинаковые | по амплитуде и частоте, | ||
сдвинутые по фазе одна от другой на угол | 2π | =120° и создаваемые общим | |
3 |
| ||
|
|
| |
источником энергии.
Каждую отдельную цепь, входящую в трехфазную цепь принято называть фазой.
Таким образом, термин "фаза" имеет в электротехнике два значения: первое – аргумент синусоидально изменяющейся величины, второе – часть многофазной системы электрических цепей.
Трехфазная цепь является частным случаем многофазных систем переменного тока.
Широкое распространение трехфазных цепей объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями:
•экономичность производства и передачи энергии по сравнению с однофазными цепями;
•возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя;
•возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.
Каждая фаза трехфазной цепи имеет стандартное наименование:
первая фаза – фаза "А"; вторая фаза – фаза "В"; третья фаза – фаза "С".
Начала и концы каждой фазы также имеют стандартные обозначения. Начала первой, второй и третьей фаз обозначаются соответственно А, В, С, а концы фаз – X, Y, Z.
Основными элементами трехфазной цепи являются: трехфазный генератор, преобразующий механическую энергию в электрическую; линии электропередач; приемники (потребители), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания).
4
2. Получение трехфазной системы ЭДС.
Трехфазный генератор создает одновременно три ЭДС, одинаковые по величине и отличающиеся по фазе на 1200.
Получение трехфазной системы ЭДС основано на принципе электромагнитной индукции, используемом в трехфазном генераторе. Трехфазный генератор представляет собой синхронную электрическую машину. Простейшая конструкция такого генератора изображена на рис. 3.1.
Рис. 3.1. Схема устройства трехфазного генератора
На статоре 1 генератора размещается трехфазная обмотка 2. Каждая фаза трехфазной обмотки статора представляет собой совокупность нескольких катушек с определенным количеством витков, расположенных в пазах статора. На рис. 3.1 каждая фаза условно изображена одним витком. Три фазы обмотки статора генератора повернуты в пространстве друг относительно друга на 1/3 часть окружности, т.е. магнитные оси фаз повернуты в пространстве на угол
23π =120°. Начала фаз обозначены буквами A, B и C, а концы – X, Y, Z.
Ротор 3 генератора представляет собой постоянный электромагнит, возбуждаемый постоянным током обмотки возбуждения 4. Ротор создает постоянное магнитное поле, силовые линии которого показаны на рис.3.1 пунктиром. При работе генератора это магнитное поле вращается вместе с ротором.
5
При вращении ротора турбиной с постоянной скоростью происходит пересечение проводников обмотки статора с силовыми линиями магнитного поля. При этом в каждой фазе индуктируется синусоидальная ЭДС.
Величина этой ЭДС определяется интенсивностью магнитного поля ротора и количеством витков в обмотке.
Частота этой ЭДС определяется частотой вращения ротора.
Поскольку все фазы обмотки статора одинаковы (имеют одинаковое количество витков) и взаимодействуют с одним и тем же магнитным полем вращающегося ротора, то ЭДС всех фаз имеют одинаковую амплитуду Em и частотуω.
| 2π | Но, так | как магнитные оси фаз в | пространстве повернуты на | угол | ||||||||
| =120°, начальные фазы их ЭДС отличаются на угол | 2π | . |
| |||||||||
3 |
|
| |||||||||||
|
|
|
|
|
|
| 3 |
|
| ||||
|
| Примем начальную фазу ЭДС фазы А, равной нулю, то есть ψеА = 0 | , | ||||||||||
| тогда | eA = Em sinωt. | (3.1) | ||||||||||
ЭДС фазы В отстает от ЭДС фазы А на |
| 2π |
|
|
|
|
| ||||||
|
|
| : |
|
|
|
|
| |||||
3 |
|
|
|
|
|
| |||||||
|
|
|
| 2π | = Em sin(ωt −120). |
| |||||||
|
|
| eB = Em sin ωt− |
|
|
| (3.2) | ||||||
|
|
|
|
| |||||||||
|
|
|
|
| 3 |
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| 2π |
| |||
ЭДС фазы С отстает от ЭДС фазы В еще на |
| : |
|
|
| ||||||||
3 |
|
|
| ||||||||||
|
|
|
| 4π | = Em sin(ωt −240). |
| |||||||
|
|
| eС = Em sin ωt− |
|
|
|
| (3.3) | |||||
|
|
|
|
|
| ||||||||
|
|
|
|
| 3 |
|
|
|
|
| |||
Действующее значение ЭДС всех фаз одинаковы:
E | A | = E | B | = E | = | Em= E | . | (3.4) |
|
| C |
| 2 | ||||
|
|
|
|
|
|
|
|
Трехфазная симметричная система ЭДС может изображаться тригонометрическими функциями, функциями комплексного переменного, графиками на временных диаграммах, векторами на векторных диаграммах.
Аналитическое изображение тригонометрическими функциями приведено в (3.1) – (3.3).
6
В комплексном виде ЭДС фаз изображаются их комплексными действующими значениями:
& | j0 | 0 | & | = Ee | − j120 | 0 | & | − j2400 |
|
|
|
| (3.5) | ||||
EA = Ee |
|
| = E; EB |
|
| ; EC = Ee |
Графики мгновенных значений трехфазной симметричной системы ЭДС на временной диаграмме показаны на рис. 3.2. Они представляют из себя три синусоиды, сдвинутые друг относительно друга на 1/3 часть периода.
Рис. 3.2. Графики мгновенных значений трехфазной симметричной системы ЭДС.
На векторной диаграмме ЭДС фаз изображаются векторами одинаковой длины, повернутыми друг относительно друга на угол 120° (рис.3.3а).
Рис. 3.3. Векторные диаграммы ЭДС трехфазных симметричных систем. (а – прямая последовательность фаз; б – обратная последовательность фаз).
7
Так как ЭДС индуктированные в обмотках статора имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на один и тот же угол 120°, полученная трехфазная система ЭДС является симметричной.
Следует отметить, что чередование во времени фазных ЭДС зависит от направления вращения ротора генератора относительно трехфазной обмотки статора. При вращении ротора по часовой стрелке, как показано на рис.3.1, полученная симметричная трехфазная система ЭДС имеет прямое чередование (А – В – С) (рис.3.3а). При вращении ротора против часовой стрелки образуется также симметричная трехфазная система ЭДС. Однако чередование фазных ЭДС во времени изменится. Такое чередование называетсяобратным (А – С – В) (рис.3.3б).
Чередование фазных ЭДС важно учитывать при анализе трехфазных цепей и устройств. Например, последовательность фаз определяет направление вращения трехфазных двигателей, и т.п. Для практического определения последовательности фаз используются специальные приборы – фазоуказатели.
По умолчанию при построении трехфазных цепей и их анализе принимается прямое чередование фазных ЭДС трехфазного источника.
На схемах обмотку статора генератора изображают как показано на рис. 3.4а с использованием принятых обозначений начал и концов фаз.
На схеме замещения трехфазный источник представлен тремя идеальными источниками ЭДС (рис.3.4б)
Рис. 3.4. Условное изображение обмотки статора генератора.
За условное положительное направление ЭДС в каждой фазе принимают направление от конца фазы к началу.
3. Способы соединения фаз в трехфазной цепи.
Для построения трехфазной цепи к каждой фазе трехфазного источника присоединяется отдельный приемник электроэнергии, либо одна фаза трехфазного приемника.
8
Рис.3.5 Схема несвязанной трехфазной цепи.
Здесь трехфазный источник представлен тремя идеальными источниками ЭДС E&A , E&B , E&C . Три фазы приемника представлены условно идеальными
элементами с полными комплексными сопротивлениями Z a ,Z b ,Z c . Каждая фаза приемника подсоединяется к соответствующей фазе источника, как показано на рис. 3.5. При этом образуются три электрические цепи, объединенные конструктивно одним трехфазным источником, т.е. трехфазная цепь. В этой цепи три фазы объединены лишь конструктивно и не имеют между собой электрической связи (электрически не связаны между собой). Такая цепь называется несвязанной трехфазной цепью и практически не используется.
На практике три фазы трехфазной цепи соединены между собой (электрически связаны).
Существуют различные способы соединения фаз трехфазных источников и трехфазных потребителей электроэнергии. Наиболее распространенными являются соединения "звезда" и "треугольник". При этом способ соединения фаз источников и фаз потребителей в трехфазных системах могут быть различными. Фазы источника обычно соединены "звездой", фазы потребителей соединяются либо "звездой", либо "треугольником".
При соединении фаз обмотки генератора (или трансформатора) "звездой" их концы X,Y иZ соединяют в одну общую точкуN, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников x, y, z также соединяют в одну точкуn (нейтральная точка приемника). Такое соединение называется соединение "звезда".
9
Рис. 3.6. Схема соединения фаз источника и приемника в звезду.
Провода A-a,B-b иC-c,соединяющие начала фаз генератора и приемника, называются линейными проводами (линейный провод А, линейный провод В, линейный провод С). ПроводN-n,соединяющий точкуN генератора с точкойn приемника, называют нейтральным проводом.
Здесь по–прежнемукаждая фаза представляет собой электрическую цепь, в которой приемник подключен к соответствующей фазе источника посредством нейтрального провода и одного из линейных проводов (пунктир на рис.3.6). Однако, в отличие от несвязанной трехфазной цепи, в линии передачи используется меньшее количество проводов. Это определяет одно из преимуществ трехфазных цепей – экономичность передачи энергии.
При соединении фаз трехфазного источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началомВ второй фазы, конецY второй фазы – с началомС третьей фазы, конец третьей фазыZ – c началом первой фазыА. НачалаА,В иС фаз подключаются с помощью трех проводов к трем фазам приемника, также соединенным способом "треугольник".
Рис. 3.7. Схема соединения фаз источника и приемника в треугольник
10
Здесь также каждая фаза представляет собой электрическую цепь, в которой приемник подключен к соответствующей фазе источника посредством двух линейных проводов (пунктир на рис.3.7). Однако в линии передачи используется еще меньшее количество проводов. Это делает передачу электроэнергии еще более экономичной
При способе соединения "треугольник" фазы приемника именуют двумя символами в соответствии с линейными проводами, к которым данная фаза подключена: фаза "ab", фаза "bc", фаза "ca". Параметры фаз обозначают
соответствующими индексами: Z ab ,Z bc ,Z ca
4. Напряжения трехфазного источника.
Трехфазный источник, соединенный способом "звезда", создает две трехфазные системы напряжения разной величины. При этом различают фазные напряжения и линейные напряжения.
На рис.3.8 показана схема замещения трехфазного источника, соединенного "звездой" и присоединенного к линии электропередачи.
Рис.3.8. Схема замещения трехфазного источника
Фазное напряжение UФ – напряжение между началом и концом фазы или между линейным проводом и нейтралью (U&A , U&B , U&C ). За условно
положительные направления фазных напряжений принимают направления от начала к концу фаз.
Линейное напряжение (UЛ) – напряжение между линейными проводами или между началами фаз (U&AB , U&BC , U&CA ). Условно положительные
направления линейных напряжений приняты от точек соответствующих первому индексу, к точкам соответствующим второму индексу (то есть, от точек с более высоким потенциалом к точкам с более низким) (рис. 3.8).
studfiles.net








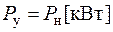



Поделиться с друзьями: