Особое внимание уделяется обеспечению качества электроэнергии, которая должна соблюдать определённые требования. Несоблюдение требований ведёт к повреждению электрического оборудования, к росту потерь электроэнергии. Ввиду постоянного роста количества электрических приёмников возникают высшие гармоники. А составляющие гармоник тока и напряжения ведут к возникновению проблем качества электрической энергии. На потребителей это сказывается в виде повышения стоимости электрической энергии. Под качеством электрической энергии принято понимать взаимосоответствие характеристик электроэнергии и показателей качества электроэнергии. Основными параметрами качества согласно ГОСТ 13109–2003 [1] являются колебания напряжения, отклонение частоты, несинусоидальность и несимметрия напряжения. Поэтому правильное определение параметров режима, таких как активная и реактивная мощность, а также действующие значения токов и напряжений имеет важное значение при исследовании показателей качества электроэнергии. Определение активной, реактивной и полной мощности. Одним из важных параметров в электроэнергетических системах является активная мощность, которой уделяется большое внимание. Активной мощностью P называется мощность, потребляемая электроприёмниками и преобразующаяся в другие виды энергии. Она имеет конкретное определение. Поэтому способы определения активной мощности никем не опровергались. Иначе можно говорить о неактивной мощности или реактивной мощности, так как стойкого определения нет. Под ней понимают всю мощность, исключая активную. Это связано с тем, что описать процессы при несинусоидальных режимах реактивной мощностью нельзя. Реактивной мощностью называют мощность, преобразующуюся в энергию магнитных и электрических полей. Электрические поля будут создаваться в электрооборудовании, которое характеризуется ёмкостным сопротивлением. Реактивная мощность в конденсаторах, кабелях представлена выражением А магнитные поля характеризуются индуктивным сопротивлением. В таких видах электрооборудования как, трансформаторы, двигатели реактивная мощность определяется выражением Полная мощность определяется общепризнанной формулой в случае синусоидальной нагрузки:
Под полной мощностью понимают мощность, необходимую для обеспечения работы нагрузки, в случае неиспользования всей мощности при совершении полезной работы. Именно она определяет выбор электрооборудования подстанций. Способов определения реактивной мощности существует много. Именно вопросы определения реактивной мощности являются предметом споров и обсуждений учёных. Внимание к этим вопросам связано с увеличением несинусоидальных нагрузок. Соответственно, если гармоники были невелики, то погрешность расчётов реактивной мощности была не большой. Рост высших гармоник связан с внедрением различных устройств. Источниками высших гармоник являются такие устройства, как сварочные аппараты, статические преобразователи, электродуговые печи. Так же фактором влияния является прогресс компьютерной техники. Что значительно сокращает время и упрощает расчёты. Ранее компьютерная и измерительная техника не позволяла производить сложные расчёты реактивной мощности. Ранее в ГОСТах никак не застрагивались несинусоидальные режимы. Поэтому проблемы определения реактивной мощности при несинусоидальных режимах являются актуальными. Международная электротехническая комиссия (МЭК) в 1977г. предложила производить расчёт реактивной мощности по формуле Методы определения реактивной мощности при синусоидальных режимах. Методы определения реактивной мощности при синусоидальных режимах можно разделить на две группы: методы, использующие мгновенные значения токов и напряжений и методы, использующие действующие значения токов и напряжений. Первая группа методов, основанная на использовании мгновенных значений токов и напряжений, использует формулу, встречающуюся практически в каждом учебнике по ТОЭ. К. С. Демирчян в [2] приводит формулу, которая справедлива лишь для синусоидального режима: Также часто встречается способ определения реактивной мощности по формуле
Формула имеет место и для расчёта несинусоидальных режимов. Также существует ещё один способ определения мощности для синусоидального режима, используя вольтамперную характеристику. Маевский в [3] предпринял попытку использования интегрального выражения. Интеграл берётся от произведения тока на функцию перпендикулярную напряжению или напротив произведения напряжения на функцию перпендикулярную тока. Мощность Маевского представлена формулой Методы определения реактивной мощности при несинусоидальных режимах. В связи с отсутствием точной формулировки реактивной мощности при несинусоидальных режимах у учёных наблюдаются большие разногласия. Наиболее известная формула расчёта реактивной мощности ввёл Штайнмец которую используют как для расчёта режимов с синусоидальной нагрузкой, так и с несинусоидальной: Далее Иловичем были предложены формула Буденау ввёл понятие «мощность искажение». Заметим, что учёные по-разному обозначают мощность искажения. В литературе [4, 5, 6] обозначают, как «D», также встречается такое обозначение, как «T» в [7]. Буденау считал целесообразным выделение двух составляющих Q и D, это являлось причиной превышения полной мощности над активной мощностью в несинусоидальном режиме. На рисунке 1 представлено геометрическое понимание мощности. Одна выражалась в сдвиге по фазе, а другая в искажении формы. Мощность искажения представлена формулой
Рис. 1. Геометрическое понимание мощностей Шклярский Я. Э. в [6] приводит формулу для расчёта мощности искажения через действующие значения токов и напряжений высших гармоник, без определения полной, активной и реактивной мощностей, в случае, когда гармонические составляющие величин заданы. Тогда мощность искажения представлена выражением В диссертации С. Н. Чижмы [5] имеется рисунок 2, на котором наглядно истолкованы понятия активной и реактивной мощности (рисунок 2). В индуктивных элементах происходит отставание тока от напряжения по фазе, в случае, когда ток и напряжение имеют разные знаки. Энергия, запасаемая в индуктивных элементах, совершает колебательные движения. Такую мощность называют реактивной. Рис. 2. Истолкование понятий активной и реактивной мощности Вывод. Одним из важных параметров в электроэнергетических системах является активная мощность, которая имеет конкретное определение. Поэтому способы определения активной мощности никем не опровергались. Иначе можно говорить о неактивной мощности или реактивной мощности, так как стойкого определения нет. Способов определения реактивной мощности существует много. Именно вопросы определения реактивной мощности являются предметом споров и обсуждений учёных. Основные термины (генерируются автоматически): реактивная мощность, активная мощность, полная мощность, режим, напряжение, мощность, действующее значение токов, мощность искажения, электрическая энергия, формула. moluch.ru Активная мощность (P) Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть P = U I потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности. Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как: P = U I Cosθ В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I. Формулы для активной мощности P = U I - в цепях постоянного тока P = U I cosθ - в однофазных цепях переменного тока P = √3 UL IL cosθ - в трёхфазных цепях переменного тока Активная мощность = √ (Полная мощность2 – Реактивная мощность2 Реактивная мощность (Q) Также её мощно было бы назвать бесполезной или безваттной мощностью. Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q). Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора. Реактивная мощность определяется, как Q = U I sinθ и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки. Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А. Формулы для реактивной мощности Q = U I sinθ Реактивная мощность = √ (Полная мощность2 – Активная мощность2) Полная мощность (S) Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной. Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью. Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности. Формула для полной мощности S = U I Полная мощность = √ (Активная мощность2 + Реактивная мощность2) Следует заметить, что: - резистор потребляет активную мощность и отдаёт её в форме тепла и света. - индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля. - конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля. Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке: Осциллятор Осцилля́тор (лат. oscillo — качаюсь) — система, совершающая колебания, то есть показатели которой периодически повторяются во времени. Гармони́ческий осцилля́тор (в классической механике) — система, которая при выведении её из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x: F=-kx где k — постоянный коэффициент. Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды. Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения. Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания. Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди немеханических аналогов гармонического осциллятора можно выделить электрический гармонический осциллятор (см. LC-цепь). Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами: • когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие; • возвращающая сила должна в точности или приближённо быть пропорциональна перемещению. • Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы . F=kx; • Потенциальная энергия частицы • Гармонический осциллятор в квантовой механике описывается уравнением Шредингера: Полная энергия осциллятора. где n=0,1,2…. cyberpedia.su Мгновенная мощность, выделяющаяся на элементах сети, определяется через мгновенные значения тока и напряжения: р = u ∙ i. Наличие сдвига по фазе между синусоидами тока и напряжения обусловливает необходимость введения понятий реактивной и полной мощности. Если цепь чисто активная (φ = 0), то графическое перемножение синусоид тока и напряжения даст нам однополярный сигнал – рис. 1.5. В любой момент времени мощность больше либо равна нулю. Эта ситуация соответствует максимально эффективному (то есть активному) потреблению электроэнергии, которая необратимо и однонаправленно выделяется на активных элементах сети и не возвращается в источник. Эта мощность получила название активной, обозначается Р и измеряется в ваттах (Вт). Рис. 1.5. Изменение токов, напряжений (а) и мощности (б) при чисто активной нагрузке (φ = 0) Если цепь имеет активно-индуктивный характер (0 < φ < 90°), то результат перемножения будет представлять собой синусоиду, поднятую относительно оси абсцисс и имеющую как положительную, так и отрицательную части – рис. 1.6. Рис. 1.6. Изменение токов, напряжений (а) и мощности (б) при активно-индуктивной нагрузке (0 < φ < 90°) Будем далее увеличивать угол φ. Когда угол достигнет 90°, получим следующий график p(t) – рис. 1.7. Среднее значение мощности за период равно нулю. Эта ситуация соответствует наиболее неэффективному (то есть неактивному или реактивному) характеру потребления электроэнергии, которая первые полпериода потребляется приёмником, а вторые полпериода возвращается обратно в источник. Эта обменная мощность получила название реактивной, обозначается Q и измеряется в варах (вар). Рис. 1.7. Изменение токов, напряжений (а) и мощности (б) при чисто индуктивной нагрузке (φ = 90°) На рис. 1.5, 1.7 рассмотрены крайние идеальные случаи, а на рис. 1.6 – промежуточная ситуация, в которой можно выделить активную и реактивную составляющие, а также величину, характеризующую их совместное действие – полную мощность S, измеряемую в вольт-амперах (ВА). Полученные три вида мощности образуют треугольник мощностей – рис. 1.8, из которого следует выражение: S = . Рис. 1.8. Треугольник мощностей Угол φ между векторами активной и полной мощностей имеет тот же смысл, что и на рис. 1.4, относящемся к сопротивлениям. Коэффициентом мощности cosφ тем больше и тем ближе к единице, чем более активный характер имеет электрическая цепь. Понятие реактивной мощности имеет особое значение в электроэнергетике. Актуальной является проблема регулирования и компенсации реактивной мощности в энергосистеме. Реактивная мощность является необходимым условием для создания магнитного поля в электрических машинах. Заметим, что в отличие от активной мощности, на создание реактивной мощности не расходуется топливо. Важно помнить, что реактивная мощность, протекающая по проводникам, приводит к активным тепловым потерям. Поэтому реактивную мощность целесообразно производить не на электростанции, а вблизи потребителя. В противном случае, реактивная мощность будет транспортироваться на большое расстояние, приводя к экономическому ущербу в виде необратимых потерь и ограничивая пропускную способность линий для передачи полезной активной мощности. Кроме того, неоправданно большие перетоки реактивной мощности приводят к падению напряжения в узлах потребления электроэнергии. Простейшими источниками реактивной мощности являются конденсаторы. Кроме того, в ряде случае излишки реактивной мощности требуется потреблять. Если этого не сделать, то повысится уровень напряжения сверх допустимого предела. Такая ситуация может сложиться при использовании длинных линий электропередачи, которые обладают значительной ёмкостью относительно земли и поэтому являются генераторами избыточной реактивной мощности. Чтобы решить данную проблему, применяют простейшие потребители реактивной мощности – шунтирующие реакторы, представляющие собой катушки индуктивности, включенные между проводником и землёй. Помимо этого используются и другие, более сложные устройства для регулирования реактивной мощности – синхронные компенсаторы и статические тиристорные компенсаторы. Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: zdamsam.ruДайте определение полной, активной и реактивной мощности. Активная и реактивная мощность определение
Методики расчёта составляющих мощности при синусоидальных и несинусоидальных режимах
 .
.  .
. 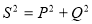 .
.  .
.  .
.  .
.  .
. 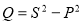 .
. 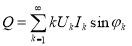 .
.  .
. 
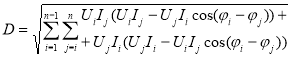 .
. 
Дайте определение полной, активной и реактивной мощности — КиберПедия
Понятие активной, реактивной и полной мощности
интернет-магазин светодиодного освещения
Пн - Вс с 10:30 до 20:00
Санкт-Петербург, просп. Энгельса, 138, корп. 1, тк ''Стройдвор''












Поделиться с друзьями: